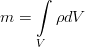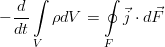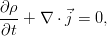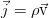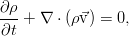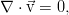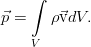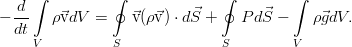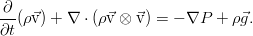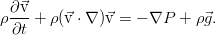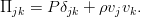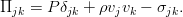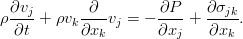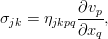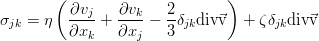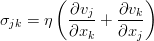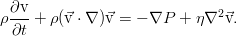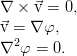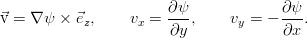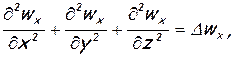Точные решения уравнений движения вязкой жидкости

Кратко о гидродинамике: уравнения движения

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

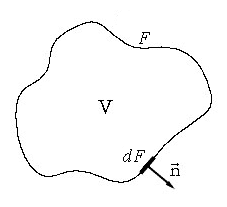
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

• конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
• давления окружающих элементов жидкости
• просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

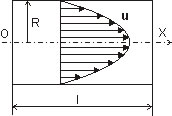
Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.

Значение именно точных решений уравнений движения вязкой жидкости Навье-Стокса Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — Выскребцов В. Г.

Исследованы решения уравнений Слёзкина Н.А. установившегося движения в ламинарном режиме вязкой несжимаемой жидкости при осесимметричном течении. На основании точного решения уравнения Слёзкина (типа Риккати) показана множественность решения этого уравнения, причём физический смысл имеет лишь небольшое число решений. Рассмотрен простейший случай безвихревых решений, для которых линиями тока могут быть окружности, эллипсы, параболы, гиперболы и прямые. Эти течения неструйные.

Похожие темы научных работ по физике , автор научной работы — Выскребцов В. Г.

VALUE OF EXACT DECISIONS OF EQUALITY OF MOTION OF VISCID LIQUID NAVIER-STOKES

The paper presents the decisions of equations of N. A. Slyozkin of steady motion in te laminary mode of incompressible viscous fluid under axisymmetrical flow. On the basis of exact decision of equation of Slyozkin (of Rikkaty-type) there is shown multiplicity of decision of this equation, thus physical sense has a small number of decisions only. The simplest case of unvortex decisions is considered, for which steam-lines can be circumferences, ellipses, parabolas, hyperbolae and lines. These flows are not stream.

Текст научной работы на тему «Значение именно точных решений уравнений движения вязкой жидкости Навье-Стокса»

Следует отметить, что в случае, когда модули упругости двух слоев равны между собой (( = Е2 ), полученная зависимость между результирующей нагрузкой Q и углом в0 , характеризующем величину зоны контакта, тождественно совпадает с аналогичной зависимостью для однослойного упругого покрытия твердого цилиндра [2].

Рисунок 2 — Зависимость между результирующей нагрузкой Q и углом в0

1. Божкова Л.В., Рябов В.Г., Норицина Г.И. Смешанная плоская задача теории упругости для двухслойной кольцевой области // Известия МГТУ «МАМИ» . М.: МАМИ, 2011, №1, — С.217-221

2. Божкова Л.В., Чебанюк А.М. Взаимодействия кольца, жестко насаженного на абсолютно твердое цилиндрическое тело, с жестким основанием. // Известия вузов. Машиностроение. — 1977., №8, с.16-22.

Значение именно точных решений уравнений движения вязкой жидкости

к. т. н. Выскребцов В. Г.

МГТУ «МАМИ» (495) 223-05-23, доб. 1465 Аннотация. Исследованы решения уравнений Слёзкина Н.А. установившегося движения в ламинарном режиме вязкой несжимаемой жидкости при осесиммет-ричном течении. На основании точного решения уравнения Слёзкина (типа Рик-кати) показана множественность решения этого уравнения, причём физический смысл имеет лишь небольшое число решений. Рассмотрен простейший случай безвихревых решений, для которых линиями тока могут быть окружности, эллипсы, параболы, гиперболы и прямые. Эти течения неструйные.

Ключевые слова: вязкая жидкость, уравнения Навье-Стокса, уравнение Риккати, точные решения.

Если движения твёрдых тел количественно описываются уравнением И. Ньютона достаточно непротиворечиво и точно в согласии с наблюдениями физических явлений, то поведение вязкой жидкости описывается, как считается, гораздо более позже выведенными уравнениями Навье-Стокса. Эти уравнения были впервые получены Л.Навье (1821г.) как уточнение уравнений Л.Эйлера (1751 г.) для невязкой жидкости и — в окончательной формулировке — Дж. Стоксом (1845 г.) [1]. С этого времени эти уравнения уже не претерпевали уточнений. Вопрос о единственности решения этих уравнений в частных производных в общем виде до сих пор не решён, если не считать исследования единственности для установившихся течений несжимаемой жидкости. Из этих исследований следует, что существует лишь небольшое число траекторий линий тока (окружности, прямые линии, а также траектории, вдоль которых вихрь скорости постоянен), удовлетворяющих указанным уравнениям движения жидкости (или более обще — уравнениям движения сплошной среды, обладающей ньютоновской вязкостью, или, как ещё говорят, уравнениям движения ньютоновских жидкостей).

В первом исследовании [2] как метод получения точных решений уравнений Навье-Стокса (или просто Стокса) применены методы дифференциальной геометрии и, как дополнительное уравнение, свойство гладкости ортогональных сетей, линиями которых служат линии тока установившегося движения частиц несжимаемой вязкой среды и ортогональными к ним линии центробежных ускорений. Во втором — используется аппарат тензорного анализа [3]. При первом подходе свойство гладкости приводит к появлению дополнительного дифференциального уравнения в частных производных относительно радиусов кривизн линий траекторий, а при втором подходе — к требованию того, чтобы тензор Римана в области течения среды был равен нулю. При этом условие гладкости сетей трактуется как движение частиц среды по траектории без ударов и скачков. Кроме того используется как существенное условие конечность (ограниченность) скоростей движения и их градиентов. Выполнение этих, представляющихся очевидными требований оказывается достаточно для однозначного решения уравнений Навье-Стокса. Эти уравнения с учётом безударности движения и ограниченных, конечных значений скоростей течения не требуют никаких дополнительных условий для однозначного решения уравнений Стокса.

Траектории течений жидкости, соответствующих нескольким из точных решений уравнений Навье-Стокса, давно наблюдались в опытах. Это ламинарное течения в прямых трубах (течение Пуазейля) и движение по окружностям между коаксиальными цилиндрами (течение Куэтта).

Наблюдение других течений, соответствующих точным решениям, из литературы не известно, хотя широко известны мнения, например, о том, что «. общая картина наблюдающихся в действительности ламинарных движений и многие их детали достаточно хорошо описывались решениями уравнений Стокса при соответствующих, также «регулярных», начальных и граничных условиях. Можно, например, вспомнить ламинарное движение вязкой жидкости в круглой трубе, соответствие теоретически рассчитанных характеристик которого (парабола распределения скоростей, формулы расхода и сопротивления) опытными данными уже блестяще подтверждено. То же относится к многочисленным другим примерам ламинарных движений вязкой жидкости: движению смазки в узких зазорах между валом и цапфой подшипника, вполне удовлетворительно описываемому гидродинамической теорией смазки подшипников, движениями в ламинарных пограничных слоях, с достаточной точностью рассчитываемых по теории.

Отмеченное совпадение результатов расчётов ламинарных течений Стокса и их применимости для теоретического описания движений вязкой жидкости. в действительности наблюдаются только те из решений уравнений Стокса, которые являются устойчивыми по отношению к возможным возмущениям. В устойчивых движениях возникшие случайно или введённые по воле исследователя в поток малые возмущения не развиваются с течением времени, а, наоборот, затухают. В противоположность этому, в неустойчивых движениях ма-

лые вначале возмущения растут, способствуя его переходу либо к новому устойчивому движению, если таковое имеется среди возможных решений уравнений Стокса, либо к некоторому хаотическому, образованному нерегулярно движущимися и взаимодействующими между собой жидкими массами. Процессы возникновения и развития такого рода движений. носят случайный характер и не поддаются строгому теоретическому анализу, требуя для своего изучения своеобразных статистических подходов.

Эта форма движений вязкой жидкости, широко распространённая природе и технических устройствах, носит название турбулентных движений» [1].

В данной работе принципиально различаются течения жидкости, описываемые точными решениями уравнений Стокса и описываемые так называемыми приближёнными решениями (с всегда неизвестной степенью приближённости), которые отождествляются с действительными течениями, такими как движение смазки в узких зазорах, течение в ламинарном пограничном слое и др.

Более того, автор считает, что именно сравнение фактических траекторий и других особенностей наблюдаемых течений и траекторий течений, определяемых из точных решений уравнений Навье-Стокса, позволяет судить о том, насколько точно описывают эти уравнения свойства жидкостей, обладающих так называемой ньютоновской вязкостью (называемых ещё ньютоновскими жидкостями).

Основания для некоторых сомнений в достаточной идентичности уравнений Стокса как количественной модели ньютоновских жидкостей известны давно, т.к. при выводе уравнений Стокса используется несколько допущений, справедливость которых неочевидна и должна быть проверена справедливостью следствий из этих допущений путём сравнения теоретических и опытных данных. В качестве первого такого неочевидного допущения отметим, что при введении понятия давления в движущейся вязкой среде используется допущение что «. в ньютоновской несжимаемой вязкой жидкости взятое с обратным знаком среднее арифметическое трёх нормальных напряжений, приложенных к взаимно перпендикулярным площадкам в данной точке среды, представляет давление в этой точке.Р. Сказанное предположение является дополнительной гипотезой к обобщённому закону Ньютона, так как, исходя из общих гидродинамических соображений, нельзя доказать, что определённая таким образом инвариантная скалярная величина Р будет той самой термодинамической характеристикой жидкости или газа, которая, например, в случае совершенного газа будет связана с другими термодинамическими характеристиками — плотностью и температурой -формулой Клайперона» [1].

В качестве другого небесспорного допущения, используемого при выводе уравнений равновесия частицы сплошной среды, является пренебрежение скручивающими эту частицу моментами внешних сил. Поясним эту ситуацию словами учебника [4]: «Предположим, что силы, приходящиеся на площадь S, статически эквивалентны силе R, приложенной к точке Q, и некоторой паре G. Если мы будем каким-то образом непрерывно уменьшать площадь S, оставляя всё время точку Q внутри её, то сила R и пара G будут стремиться к нулю, а направление силы — к некоторому предельному направлению (l,m,n). Мы предположим, что число R/S, полученное путём деления числа единиц силы в силе R на число единиц площади в площади S, стремится к нулю к некоторому пределу F, а отношение G/S стремится к нулю». Таким образом, отсюда следует, что при рассмотрении равновесия отдельной твёрдой частицы момент кручения от действия внешних сил и соответственное угловое ускорение согласно теоретической механике должно учитываться и учитывается, а вот при рассмотрении жидкой частицы — нет, не учитывается. Возможно, что обстоятельство может служить признаком того, что уравнения Стокса, как и уравнения теории упругости сплошной среды, могут описывать лишь незакрученные движения и поля напряжений, т.е. только плоские и осесимметричные.

Только сравнением теоретических, соответствующих точным решениям уравнений

Стокса и фактических, физически наблюдаемых течений может быть определена справедливость вышеуказанных допущений. Затруднением здесь служило то, что уравнения Стокса представляют собой нелинейные дифференциальные уравнения второго порядка в частных производных, теория которых недостаточно разработана. Однако с учётом того, что уравнения Стокса прежде всего должны рассматриваться с позиций уравнений движения физической частицы, а не с позиций чисто математических выражений и поэтому с учётом условия движения частиц среды без ударов и скачков и, кроме того, с использованием как существенного условия конечности (ограниченности) скоростей движения и градиентов скорости в [2, 3], удалось получить описание траекторий всех точных решений уравнений Стокса. Подчеркнём, что различными математическими методами был получен один и тот же результат, правда, при следующих ограничениях: движение установившееся, среда несжимаемая. Некоторая неясность оставалась только для осесимметричных течений.

Согласно популярным в 60-е годы и переиздаваемом до сих пор учебнике «Фейнманов-ские лекции по физике» [5] уравнения Навье-Стокса характеризуются следующим образом: «. наши уравнения для Солнца, например, представляющие его как водородный шар, описывают Солнце без солнечных пятен, без зернистой структуры его поверхности, без неровностей и короны. Тем не менее, всё это действительно находится в уравнениях, только у нас ещё нет способа вытащить их оттуда. сегодня мы не можем увидеть в уравнениях потока воды такие вещи, как спиральное строение турбулентности, которую мы видим между вращающимися цилиндрами. Сегодня мы не можем сказать с уверенностью, содержит ли уравнение Шредингера и лягушек, и композиторов, и даже мораль или там ничего похожего и быть не может. Мы не можем сказать, требуется ли что-либо сверх уравнения, вроде каких-то богов, или нет.».

Таким образом, американские авторы «Фейнмановских лекций» склоняются к мысли, что в уравнениях Навье-Стокса «всё есть», но «нет ещё способа вытащить». Сказанное объясняет интерес к именно точным решениям уравнений Стокса и соответствующим им реальным течениям.

Поскольку плоские течения уже рассмотрены достаточно подробно (кроме случая постоянства вихря скорости) в [2, 3], то в данной работе рассмотрены автомодельные, то есть подобные, установившиеся течения вязкой несжимаемой среды, в некотором смысле переходные от плоских к пространственным.

Уравнения Стокса для установившихся автомодельных осесимметричных движений несжимаемой среды, как показано было впервые Н.А.Слёзкиным (1934 г.) [6], записанные в сферической системе координат, с учётом осесимметрии сводятся к одному обыкновенному, с одной независимой переменной, дифференциальному уравнению первого порядка типа Риккати относительно некой функцииf(п), которая пропорциональна функции тока: 2 (1 — п2) f 1 (п) — f 2(П) + 4 п f( П )+ Cm2 + С2П + C3 = 0 . (1)

В этом уравнении С1, С2, С3 — постоянные интегрирования, которые, возможно, должны определяться граничными условиями. Решение дифференциального уравнения первого порядка Риккати общего вида:

?п = Р(п) f2rn)+ Q(rn) Дп) + к-(п),

как показал Лиувилль, за исключением очень немногочисленных частных случаев, не сводится к квадратурам и не может быть выражено в конечном виде через элементарные функции [7]. Подстановкой

ад = — уу (У(п) Р(п)) = — 2 (1 — п2) YV У(п) , (2)

где: Р(п) — коэффициент при квадратичном члене уравнения Риккати позволяет привести исходное уравнение (1) к однородному линейному уравнению второго порядка. Для рассматриваемого уравнения (1) это позволяет перейти к уравнению второго порядка с переменными коэффициентами вида:

Раздел 3. Естественные науки.

Получив уравнение (1) Слёзкин не решал его, а ограничился указанием, что выведенное им уравнение «можно исследовать» [6]. Впоследствии уравнение (1) многократно [1, 8 и др.] выводилось разными авторами. Изложенный далее вывод предложен Лойцянским [1].

В соответствии с теорией подобия из анализа размерности следует, что для автомодельных течений вязкой среды поле скоростей и давлений может быть представлено в осе-симметричной сферической системе координат (R, п = cos в), где R — расстояние от начала координат, а в — угол между радиус-вектором рассматриваемой точки среды и осью течения, в форме:

Vr = — v f!(n)/ R, Ув = — vf(n)/(R -П2 ) . (4)

Течение с такими проекциями скоростей будет безвихревое, если: f 11 (п) = 0. Определив функцию f(cose = п) из уравнения (1), можно согласно (4) найти составляющие скорости течения VR и Ve и затем траекторию течения как [7]:

dR/VR = R ёв/ Ув . (5)

Отсюда в соответствии с представлением (4) получим дифференциальное уравнение, которое легко интегрируется:

Здесь С0 — постоянная интегрирования, cos в = п. Таким образом, для наблюдений и экспериментов определяющим является решение уравнения (1) в виде функции f(п). Первое точное решение этого уравнения было указано для случая C1 = C2 = C3 = 0 Ландау [1, 9], который обосновал выбор неопределённых постоянных тем, что при этом получается нетривиальное аналитическое решение. Действительно, при этом допущении уравнение (1) является уравнением типа Бернулли и решается известными способами [7]. Уравнение (3) приобретает при этом вид: Y = 0. Отсюда согласно (2) получим

^(п) = 2 (1 — п2)/(А + 1 — п) , (7)

где: А — постоянная интегрирования. Как считали Ладау и Лойцянский [1,7] постоянная А зависит от величины проекции на ось течения полного импульса потока, «включающего количество движения, давление и вязкие напряжения».

Впоследствии выяснилось, что помимо решения Ландау уравнение Слёзкина допускает ряд других точных решений при различных частных значениях постоянных, указанных Седовым [10]. Дело в том, что уравнение (3) меняет свой тип в зависимости от частных значений неопределённых постоянных С1, С2 и С3. Седовым указаны случаи:

10. (1 + п)2 Y11 — C1 У(п)/4 = 0 при С2 = — 2 Сь Сз = Сь (3а)

20. (1 -п)2 Y11 — C1 У(п)/4 = 0 при С2 = 2 Сь С3 = С1; (3б)

30. (1 — п2) У11 + C1 У(п)/4 = 0 при С2 = 0, С3 = — С1. (3в)

Уравнение (3 а) представляет собой уравнение Эйлера и сводится к линейному уравнению с постоянными коэффициентами заменой 1 + п= exp(t). Аналогичной заменой 1 — п = exp(t) решается и уравнение (3б). Уравнение (3в) имеет простое решение, а именно: У(п) = a (1 — п2), где a = const, C = 8.

Таким образом, варьируя значения постоянных в исходном уравнении (1), можно получать точные решения уравнения Слёзкина разного аналитического вида. Докажем теперь более общее утверждение: уравнение Слёзкина, являющееся частным случаем уравнений На-вье-Стокса при осесимметричном движении вязкой несжимаемой жидкости, имеет бесконечно много точных линейно независимых аналитических решений.

Для доказательства, как и ранее [11], будем искать решения уравнения (3) в виде многочлена с постоянными коэффициентами степени N, мотивируя это тем, что поскольку уравнение (3) линейно и имеет коэффициентами многочлены, то и решение может иметь вид

Y(n) = ao + ai r\ + П + . + aN nN, здесь N = 1, 2, 3, 4, 5 .

Дифференцируя это выражение дважды и подставляя его в (3), получим многочлен (N +2) степени, коэффициенты которого должны быть равны нулю. Это даёт N +3 уравнения для определения N + 1 коэффициентов a при трёх произвольных постоянных С1, С2, С3, т.е. всего N +4 неизвестных постоянных. Одна из постоянных (например, aN) остаётся неопределённой и играет роль общего множителя. Однако поскольку для определения функции f(n) согласно (3) требуется отношение производной Y(n) и самой функции, то общий множитель aN при этом сократится. Неопределённым останется только степень многочлена.

Для иллюстрации этого будем искать значение Y(n) в виде многочлена, например, третьей степени, а именно в виде: Y(n) = a0 + a1 r\ + a2 ц2 + a3 ц3. Тогда вторая производная окажется равной: Yn(tf) = 2a2 + 6 а3ц. Подставляя указанные значения в уравнение (3) и приравнивая к нулю коэффициенты при равных степенях, получим следующую систему уравнений:

Коэффициент при п5 24 a3 — C1 a3 = 0;

Коэффициент при п4 8 a2 — C1 a — C2 a3 = 0;

Коэффициент при цъ: — 48 a3 — C1 a1 — C2 a2 — C3 a3 = 0;

Коэффициент при ц2: — 16 a2 — C1 a0 — C2 a1 — C3 a2 = 0;

Коэффициент при n: 24 a3 — C2 a0 — C3 a1 = 0;

Коэффициент при 8 a2 — C3 a0 = 0.

Из первого уравнения, которое можно записать в виде a3 (24 — С1) = 0, следует вывод, что поскольку по смыслу поиска решения как многочлена третьей степени a3 Ф 0, то С1 = 24. Если же решение искать в виде многочлена N-й степени, то из тех же соображений получим для С1 = 4 N (N -1), N — целое. Поэтому в зависимости от выбранной степени многочлена Y(n) получим возрастающие значения коэффициента: С1 = 0; 8; 24; 48; 80 и т.д.

Подставляя в приведённую выше систему оставшихся пяти уравнений С1 = 24 получим новое точное решение уравнение Слёзкина (а с ним и системы уравнений Навье-Стокса) в виде:

f2 (n) = 2 (3П- 1)/ П. (9)

Очевидно, что подобных точных решений уравнений Стокса указанным методом можно найти неопределённо много. Причём чем больше степень многочлена Y(т]), тем более точное, казалось бы, можно получить решение.

Определённость может внести то обстоятельство, что решения уравнений Стокса должны не только удовлетворять этим уравнениям только с формальной, чисто математической стороны, но и соответствовать картине некоторого реального течения, наблюдаемого в опытах. Чтобы проиллюстрировать это, рассмотрим ранее уже исследованное автором осе-симметричное течение, для которого [11]:

f3 (n) = E1 (m +п). Здесь: Е1, m = const. (10)

Для этого решения уравнения Слёзкина оказывается, что: Y(n) = C (1 — т]2)E, где С -неопределённая постоянная, здесь E = Ej(1 — m)/4. Решение (9) безвихревое, т.к. вторая производная отf3 (п) равна нулю.

Траектории течения, которому соответствует решение вида (8), будут выражаться согласно (5) как

Переходя к декартовой системе координат заменой: х2 + y2 = R2, cos в = п = y/R, получим следующее выражение для уравнения траекторий:

x2 + y2 = (Co — x/m)2 . (12)

Здесь Со = С/(Е> m) — новая постоянная. При m2 = 1 уравнение (12) представляет собой уравнение семейства парабол, пересекающих ось симметрии и пересекающих ось симметрии в точке 2 Со :

y2 = 2 Co (Co/2 — x) .

Если же т Ф 1, то уравнение (12) может быть преобразовано и представлено в виде:

C02m4/(m2 -1)2 + Co2m2/(m2 -1)

Согласно [14] траектории течения, соответствующие решению (9) представляют собой в зависимости от значения т либо семейство эллипсов (при т2 > 1), либо семейство гипербол (при т2 1 уместно рассматривать как линии тока в виде эллипсов при вытекании из боковой поверхности пористой трубки слева, и втекания справа, как на рисунке 1. Параболические траектории (при т2 = 1) можно интерпретировать с учётом знаков для ¥я и V0 как линии тока вытекания из боковой поверхности центральной пористой трубки в окружающую жидкость. Коэффициент С0 играет роль масштабного фактора. Чем больше Со, тем на большем удалении от начала координат расположена траектория течения.

Рисунок 1 — Схема линий тока, соответствующих линейному точному решению уравнения Слёзкина Н.А. для осесимметричных течений при разных значениях параметра т. Траектории имеют форму парабол при т = 1, эллипсов при т > 1,

гипербол при т Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Явление длительного сохранения слабой остаточной завихрённости в объёме залитой в ёмкость воды известно давно, хотя и необъяснено. Так, Шиллер [14] указывает, что, несмотря на, казалось бы, слабую остаточную завихрённость, значение числа Рейнольдса в круглой трубе, вода в которую поступает из ёмкости достаточно большого размера, сильно зависит от времени отстаивания воды в ёмкости. Значение критического числа Рейнольдса может меняться примерно от Яе = 950 для свежезалитой воды и примерно до Яе = 25 000, причём последнее значение наблюдается при отстаивании воды в течение трёх суток и более. Таким образом, один из важнейших критериев современной гидравлики может меняться при прочих равных условиях более чем в 25 раз. Заметно уменьшить влияние остаточных вихрей при наполнении ёмкости можно использованием капельного метода, когда вода в ёмкость заливается не струёй, а по каплям, с помощью лейки в виде душа. Однако этот способ заполнения сильно удлиняет проведение опытов.

Описанная существенная разница в характере траекторий втекающей и вытекающей через пористую цилиндрическую боковую поверхность воды должна иметь теоретическое обоснование. И оно находится, если принять во внимание закон сохранения энергии для жидкой частицы, в форме Бернулли [1].

Действительно, рассмотрим течение в боковую поверхность (или из боковой поверхности) трубки согласно схеме рисунка 1 на удалении от начала координат, где линии тока как эллиптического типа, так и параболического или гиперболического типов можно считать прямыми. Тогда течение, рассматриваемое в поперечном сечении, будет соответствовать классическим линиям тока или источника [1] в виде пересекающихся в одной точке прямых линий (лучей, выходящих из начала координат). Рассмотрим на одной из линий тока две точки — М1 и М2. Обозначим скорости движения жидкости в точках соответственно через V1 и ¥2 , а давления — соответственно через Р] и Р2 (рисунок 5).

Рисунок 5 — Характер линий тока при всасывании воды в боковую пористую поверхность цилиндра. Линии тока соответствуют линиям плоского точечного стока

При движении жидкости вдоль прямолинейных, пересекающихся в одной точке траекторий, движение среды происходит аналогично картине движения плоского безвихревого течения при так называемой идеальной (не имеющей вязкости) жидкости. Такое течение называют источником (стоком) [1]. Поэтому можно считать, что для этого течения применим интеграл Бернулли, смыслом которого является равенство суммы кинетических и потенциальных энергий жидкой частицы при движении по траектории. Отсюда, считая жидкость однородной, плотностью р и считая, что движение происходит на одном уровне, т.е. пренебрегая изменением потенциальной энергии положения, получим согласно [1]:

V2/2 + P1/р = V2/2 + P2/ р = const. (15)

Пусть точка М2 неопределённо удалена от начала координат, а точка М1 — близка (рисунок 5). Тогда, считая по прежнему жидкость несжимаемой, получим, что V2 на удалении близка к нулю, а давление Р2 близко к некоторому постоянному значению Р0. Пренебрегая в силу малости V2 по сравнению с V1 , получим из предыдущего выражения:

(Р1 — Р2)/р = — У2/2 1

Рисунок 7 — К вычислению расхода жидкости, всасываемой боковой поверхностью

трубки с равномерной пористостью стенки

Таким образом, коэффициент Е> может быть истолкован как величина, пропорциональная удельному линейному расходу dq/dR через стенки центрально расположенной трубки с пористой стенкой. Общий расход из боковых стенок пористой трубки на её длине R будет равен: Q1 = — 2л V Е> (т + 1)К

Если провести сферу с центром в начале координат с центром радиусом R, то расход жидкости Q2 через эту сферу будет равен произведению радиальной составляющей скорости VR (которая для неструйного решения не зависит от полярного угла в) и площади сферы при любом значении т:

02 = — 4 л R2 Ук = — 4 ЛV Бх R. (17)

Таким образом, для параболических траекторий (при т = 1) получим: Q1 = Q2. Коэффициент Е1 можно истолковать как величину, пропорциональную удельному расходу истекающей из центральной оси среды, либо как величину, пропорциональную расходу через поверхность единичного шара, имеющего центр в начале координат при течении жидкости по параболическим траекториям. Поскольку физические величины (плотность, объём и т.д.) обычно считают положительными, то и расход Q должен быть больше нуля, а тогда для параболического течения (т = 1) должно быть Е1 Надоели баннеры? Вы всегда можете отключить рекламу.

УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОЙ ЖИДКОСТИ

Особенности напряженного состояния вязкой жидкости.

Нормальные и касательные напряжения. Тензор напряжений.

Закон трения Ньютона. Законом трения Стокса.

Поперечный и продольной градиент скорости.

Динамический и кинематический коэффициент вязкости.

Скорости угловой и линейной деформации. Тензор скоростей деформаций

Давление в вязкой жидкости. «Вторая вязкость».

Уравнение Навье Стокса.

Уравнения движения идеальной жидкости рассматривались в разделе Уравнения движения[1], где они были представлены в форме Эйлера и в форме Громеки. В настоящем разделе изучается движение вязкой жидкости. Это более сложное явление. В отличие от идеальной жидкости, где поверхностными силами являются только силы нормального давления (нормальные напряжения сжатия), в вязкой жидкости эти силы получаются несколько иными, а именно: появляются касательные напряжения, приложенные к поверхностям, которые ограничивают рассматриваемый объем, нормальные напряжения зависят не только от давления, но и от сил вязкости.

Уравнения движения вязкой жидкости выводятся тем же методом, что и уравнения Эйлера, только расширяется комплект действующих сил — добавляются касательные напряжения, а нормальные напряжения вычисляются более сложно. Поэтому, прежде чем приступить к выводу, необходимо выяснить, как определяются напряжения.

В элементарном объеме, изображенном на рисунке 5, полагая, что жидкость вязкая, векторы поверхностных сил будут направлены не перпендикулярно к площадкам (например, АDЕF, ВСКL), а под косыми углами к ним. Это связано с тем, что векторы напряжений поверхностных сил имеют не только нормальные компоненты, но и касательные. Заметим также, что в теории вязкой жидкости положительными нормальными напряжениями считаются напряжения растяжения. Поэтому на схемах подобных рисунку 5, напряжения от поверхностных сил изображают векторами, направленными не внутрь рассматриваемого объема, а наружу.

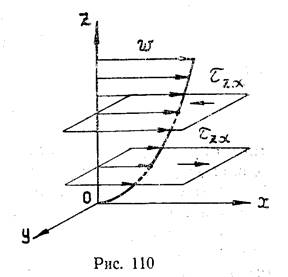
Для обозначения проекций вектора напряжения поверхностной силы применяется двойная индексация. Первый индекс указывает ту площадку, на которой рассматриваются напряжения. Этому индексу дается наименование той координатной оси, которая нормальна к заданной площадке. Так, например, для площадки, параллельной координатной плоскости хоу, при обозначении любых напряжений первым индексом будет z. Второй индекс указывает ту ось, на которую проектируется вектор напряжения. Таким образом, на каждой площадке рассматриваются два касательных и одно нормальное напряжение. Касательные имеют разноименные индексы, нормальные — одноименные (см. рисунок 109).

Поскольку частицу жидкости можно представить как элементарный объем кубической формы, то вполне очевидно, что для характеристики ее напряженного состояния нужно задать следующие девять величин:

Если составить моменты сил, вызываемые касательными напряжениями, приложенными к граням кубика, и рассмотреть условия их равновесия относительно координатных осей [2], то нетрудно доказать, что

т.е. касательные напряжения, приложенные к смежным граням и действующие в одной плоскости, численно равны. Это дает значительное упрощение, так как позволяет сократить число рассматриваемых напряжений с девяти до шести.

Для дальнейших рассуждений необходимо связать напряжения со скоростью движения жидкости.

Наиболее простую зависимость касательных напряжений от скорости дает закон жидкостного трения Ньютона

(6.1)

Здесь τ — касательное напряжение, ∂w/∂n — изменение скорости по нормали к линии тока, или поперечный градиент скорости. Коэффициент пропорциональности в этой формуле μ — называется динамическим коэффициентом вязкости, или динамической вязкостью. Он зависит от рода жидкости и характеризует вязкость. Кроме того, он зависит от температуры. Для капельных жидкостей с ростом температуры и уменьшается, следуя зависимости

(6.2)

где а и b — постоянные для данного рода жидкости коэффициенты, t — температура в градусах Цельсия, μ₀ — динамический коэффициент вязкости при t=0°. Для газов μ возрастает с увеличением температуры. Эта зависимость хорошо описывается формулой Сатерлэнда

(6.3)

в которой с — коэффициент, зависящий только от рода газа, Т — абсолютная температура в градусах Кельвина, μ₀ — коэффициент вязкости при Т=Т₀. Для воздуха можно пользоваться также приближенной зависимостью

(6.4)

Наряду с динамическим коэффициентом вязкости применяется еще кинематический коэффициент вязкости

(6.5)

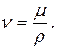
Его размерность [м 2 /сек] не содержит динамических величин, а только кинематические, откуда он и получил свое название.

Единицы измерения дляμ и ν в различных системах следующие:

СИ	СГС	МКГС (техническая)
μ	1	1	1
ν	1	1	1

В системе СГС эти единицы имеют специальные названия: 1 дин сек/см 2 = 1 пуаз; 1 см 2 /сек = 1 стокс. Соотношение между единицами в различных системах такое:

Применяя формулу Ньютона (6.1) к потоку, движущемуся параллельно плоскости хоу (см. рисунок 110), можно записать

(6.6)

Если рассмотреть два бесконечно близко расположенных слоя, которые на рисунке 110 изображены параллельными плоскостями, то можно заметить, что касательные напряжения на верхний слой со стороны нижнего действуют против движения, а на нижний со стороны верхнего — по движению. Иначе говоря, верхний слой стремится увлечь за собой нижний, а нижний слой тормозит верхний. Объем жидкости, находящийся между такими слоями, деформируется, получая деформацию сдвига (см. рисунок 111). Согласно формуле (1.5)[3] скорость угловой деформации определится как

что при =0 (так как w_z=0) даст

(6.7)

Таким образом, между касательным напряжением и скоростью угловой деформации существует линейная зависимость с коэффициентом пропорциональности 2μ.

В более общем виде связь между напряжениями и скоростями деформации жидкости устана­вливается законом трения Стокса. Этот закон имеет формальную аналогию с законом Гука для твердого тела, применяемом в теории упругости или в сопротивлении мате­риалов. По закону Гука напряжения, возникающие в твердом теле, пропорциональны деформациям: нормальные напряжения пропорциональны линейным относительным деформациям, а касательные — угловым. Согласно закону Стокса напря­же­ния пропорциональны не деформациям, а скоростям деформации: нормальные — скорости линейной деформации, а касательные — скорости угловой деформации. Коэффициент пропорциональности, как это следует из рассмотренного выше частного примера, равен 2μ [4].

Обращаясь к теореме Коши-Гельмгольца (1.7)[5] видим, что при движении жидкого объема в общем случае имеют место следующие скорости деформации:

скорости линейной деформации

скорости угловой деформации

Тогда, принимая во внимание формулы (1.5), можно записать касательные напряжения в таком виде:

(6.8)

а нормальные напряжения, возникающие только от действия сил вязкости, представить так:

(6.9)

Нужно обратить внимание, что полные величины нормальных напряжений р_хх, р_уу, р_zz отличаются от записанных формулой (6.9) на величину давления в газе р₀, которое определяется молекулярно-кинетическими процессами. (Давление в газе или жидкости существует и тогда, когда влияние вязкости отсутствует, например, в идеальной жидкости или в неподвижной реальной жидкости). Таким образом,

(6.10)

Знак минус перед величиной р₀ связан с тем, что давление создает напряжения сжатия, в то время как положительными считаются нормальные напряжения растяжения.

Вычитая из утроенной величины р_xх сумму напряжений, можно записать

(6.11)

Теперь следует ввести понятие о том, что такое давление в вязкой жидкости.

Если за величину давления принять нормальные напряжения р_хх, р_yy, р_zz, то возникает неудобство, так как в одной и той же точке эти напряжения различны по величине. В этом случае пришлось бы в каждом направлении рассматривать свою величину давления. Для того чтобы понятия давления в вязкой жидкости и в идеальной жидкости сохранялись идентичными, надо отыскать такую комбинацию, составленную из трех напряжений р_хх, р_yy и р_zz, которая не зависела бы от ориентации системы координат, иначе говоря, которая не зависела бы от ориентации площадки, проведенной внутри жидкости для подсчета действующих на нее сил давления. Таким свойством обладает средняя арифметическая величина

Она и принимается в качестве давления в вязкой жидкости.

Пользуясь таким представлением о давлении, можно записать выражение (6.11) для р_хх и аналогичные ему для р_yy и р_zz в следующем виде:

(6.13)

В случае несжимаемой жидкости, согласно уравнению неразрывности divw=0, тогда последние слагаемые в правой части обращаются в нуль и уравнения (6.13) упрощаются. Сопоставляя их с формулами (6.10), нетрудно заметить, что в этом случае р=р₀.

Попутно заметим, что «давление движущейся жидкости имеет свойства гидростатического, если не учитывать сил вязкости. Действительно, для невязкой жидкости силы, являющиеся причиной движения, не отличаются от сил, действующих в покоящейся жидкости (массовые силы, силы инерции). Поэтому доказательство того, что давление образует скалярное поле (см. Гидростатику), полностью распространяется и на движущуюся невязкую жидкость».

Для вывода уравнений движения вязкой жидкости рассмотрим элементарный объем АВСDЕFLК (см. рисунок 112), движущийся под действием сил: поверхностных нормальных , поверхностных касательных и массовых . Равнодействующая этих сил, в соответствии со вторым законом Ньютона, должна равняться массе жидкого объема, умноженной на ускорение. Запишем это уравнение сначала в проекциях на ось x, подсчитав предварительно проекции действующих сил

здесь — масса, а — проекция ускорения на ось х. После подстановки сюда вычисленных значений проекций сил, приведения подобных и сокращения на , это уравнение приобретает вид:

(6.14)

Подставим теперь вместо напряжений их выражения через скорости деформаций, пользуясь формулами (6.13) и (6.8) и считая μ=соnst. Тогда

и уравнение (6.14) после небольших преобразований принимает такой вид:

Применяя здесь операторы Δ и div

Поделив обе части равенства на ρ и приняв во внимание, что , представим уравнение движения в проекциях на ось х и аналогичные ему в проекциях на оси у и z в окончательном виде

(6.15)

Они называются уравнениями Навье-Стокса [6].

В заключение нужно отметить, что существует кроме зависимости (6.12) еще одна, которая может представлять давление в вязкой жидкости, а именно

Эта величина также не зависит от ориентации площадки, на которую рассматривается действие сил давления. Коэффициент μ’ называется второй вязкостью.

На формальную возможность такого представления давления указывали еще Стокс и Кирхгоф, однако физическое истолкование явление второй вязкости получило в 1937 году в работах Л.И.Мандельштама и М.А.Леонтовича. Вторая вязкость связана с явлениями неравновесности и проявляется в быстропротекающих процессах. Если в движущемся газе происходит очень быстрое изменение плотности, то наблюдается некоторое отставание в изменении других величин. Восстановление равновесия протекает с диссипацией энергии, т.е. с необратимым преобразованием части энергии в тепло. Таким образом, этот эффект аналогичен вязкости.

Если провести вывод уравнений Навье–Стокса, воспользовавшись формулой (6.16) вместо (6.12), то они принимают такой вид:

(6.17)

Нужно заметить, что в несжимаемой жидкости вторая вязкость не проявляется (divw=0), а в газах при сравнительно медленных процессах последний член в формуле (6.16) мал, поэтому в обычных случаях давление в вязкой жидкости определяют по формуле (6.12), а уравнения Навье — Стокса берут в форме (6.15).

«Дифференциальные уравнения газовой динамики, записанные в координатной форме, сложны, их вывод требует большого времени и большого количества бумаги. Значительно удобнее при их получении использовать векторную алгебру и самые начала тензорного анализа: тензорные обозначения и простейшие тензорные преобразования».