Статья «Будущее математики-это уравнение с пятью неизвестными»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
ГОУ СПО ЛНР «Луганский строительный колледж»
Л.В. Еськова, преподаватель математики
БУДУЩЕЕ МАТЕМАТИКИ — ЭТО УРАВНЕНИЕ С ПЯТЬЮ НЕИЗВЕСТНЫМИ…
Что ожидает математику в будущем? Эпоха великих математических открытий или математика от догматики определений перейдет к математике динамических систем? Н а стыке каких наук будет активно развиваться математика в ближайшие 20-30 лет?
Лучший метод для предвидения будущего развития математических наук заключается в изучении истории и нынешнего состояния этих наук.
Такой прием исследования является для математиков некоторым образом профессиональным. Ведь они привыкли экстраполировать , т. е. выводить будущее из прошедшего и настоящего, а так как ценность этого приема хорошо известна, то велика вероятность надежности тех результатов, которые могут быть получены с его помощью.
Последнее время прогнозы развития цивилизации основываются на математических (компьютерных) расчётах, и часто эти прогнозы пессимистичны. Сбудутся эти прогнозы или нет, но будущее чистой математики должно разительно отличаться от ее прошлого. В 1875 году любой грамотный математик мог полностью усвоить доказательства всех существовавших на тот период теорем за несколько месяцев. В 1975 году, за год до того, как была доказана теорема о четырех цветах, об этом уже не могло быть и речи, однако отдельные математики еще могли теоретически разобраться с доказательством любой известной теоремы. К 2075 году многие области чистой математики будут построены на использовании теорем, доказательства которых не сможет полностью понять ни один из живущих на Земле математиков — ни в одиночку, ни коллективными усилиями. Многие математики будут по-прежнему доказывать теоремы традиционными методами, но это будут уже лишь отдельные ностальгические островки в океане новой математической дисциплины. Будет широко применяться формальная проверка сложных доказательств, однако достижение общественного консенсуса будет столь же распространенным условием для принятия того или иного результата, что и строгое доказательство. Возможно также, что к тому времени грань между математикой и другими науками сотрется настолько, что философские вопросы об уникальном статусе предмета математики станут анахронизмом.
Большая часть современных технологий основана на математике — когда мы говорим о цифровой экономике или новом технологическом укладе, надо понимать, что это потребует работы математиков и хорошей математической подготовки людей многих других профессий.
Доктор физико-математических наук, заведующий отделом моделирования нелинейных процессов Института прикладной математики РАМ им. Келдыша Г.Г. Малинецкий на конференции по математическому моделированию истории сказал: «Еще великий Гаусс хотел вывести уравнения для общественной жизни, чтобы прогнозировать будущее. И потом такие попытки предпринимались неоднократно, но безуспешно. История оказалась слишком сложной даже для всемогущей математики». Сейчас на альянс истории и математики появился спрос. Дело в том, что человечество становится все более могущественным, и каждое его неверное движение может привести уже в ближайшем будущем к последствиям, которые могут оказаться катастрофическими как для него, так и всей планеты. Поэтому нельзя и дальше учиться методом проб и ошибок. Нужно заранее знать, к чему приведет каждый шаг. Заглянуть в это будущее должен помочь союз математики и истории.
Великий философ Кант говорил: в каждой области знаний столько науки, сколько в ней математики. Конечно, наивно думать, что кто-то составит уравнение революций или проведения реформ. Но историк в союзе с математиком уже способны дать конкретные ответы на многие конкретные вопросы. Например, почему так часто были властные перевороты в Древнем Египте или Китае? Или почему Великий шелковый путь возникал и исчезал с удивительной периодичностью? Причем это будут не десять вариантов ответа, а всего 1-2. То есть история перестает быть наукой мнений, становится точной, формализованной. Нередко именно математики помогают историкам составлять модели исторических событий, основываясь на своем богатом опыте. Оказалось, что самые разные, вроде бы совсем далекие друг от друга процессы, скажем, в химии, биологии, социологии, астрономии, энергетике описываются одними и теми же уравнениями. Поэтому, увидев определенные аналогии, математик может подсказать специалисту, как строить модель событий. И результаты получаются совершенно неожиданные. Получается, что имея самую прекрасную модель прошлого, можно прогнозировать будущее.
Чтобы с помощью математических моделей заглядывать в будущее, надо найти в прошлом период, примерно аналогичный нынешнему. И имея для него математическую модель, проиграть на ней самые разные варианты событий, в зависимости от действий власти, общества, внешних факторов и т.д. Тогда можно выбирать тот путь развития, который представляется оптимальным.
Когда закончится экономический кризис? Наступит ли глобальное потепление? Когда начнется III мировая война? Обращаться к экстрасенсам или гадалкам не обязательно, на эти вопросы вполне может обоснованно ответить математическая статистика. Но при одном условии – наличии массива данных для анализа.
Когда в опытно-конструкторском бюро имени П.О. Сухого спросили: «Расскажите, какой самолет нужен через 30 лет?», то получили ответ: «Конструкторы не могут этого сделать. Это могут сделать только математики, специалисты по прогнозам». И эта работа была сделана. И эти самолеты сейчас летают.
Более того, оказалось, что математика, прикладная математика, она в состоянии найти месторождения, самые экзотические. Было найдено несколько крупных месторождений золота благодаря тому, что были предложены новые алгоритмы поиска. Это стало возможным благодаря построению компьютерной модели усилиями геологов и математиков.
Джею Форрестеру , американскому системному аналитику и его команде предложили заглянуть в будущее. Он сделал очень простую вещь. Он взял ключевые переменные, которыми характеризуют человечество, а именно: ресурсы, основные фонды, доля фондов в сельском хозяйстве, качество жизни, уровень загрязнения — и связал их системой уравнений. Он связал их так, чтобы они идеально повторяли траекторию до 1970 года. То, что он увидел, изображено на рис.1. Что происходит? При сохранении технологий ресурсов становится все меньше, нам нечем расплатиться за то, чтобы окружающую среду должным образом очищать и оберегать. Ну и дальше начинается коллапс. Среда становится хуже, ресурсы — дороже, ну и так далее. Коллапс к 2050 году.
Развитие всё более совершенного и мощного компьютерного программного обеспечения, не оставляет сомнений в том, что вероятность появления ученых, способных охватить умом все аспекты сложного математического доказательства, неуклонно стремится к нулю. Двадцатый век полностью обеспечил условия решительного и необратимого изменения природы математических исследований. Чистая математика всё еще остается наиболее достоверной отраслью знаний, но ее притязания на уникальный статус становятся всё менее обоснованными.
Вот почему постепенно все большую и большую роль в выполнении математических вычислений, начиная от самых простых и кончая самыми сложными, стали играть ЭВМ и позже ПК. Стало зарождаться новое понятие и направление на стыке математики и новых информационных технологий — компьютерная математика. Важно отметить, что компьютерная математика является частью прикладной и классической математики. Широкое распространение получили системы математического моделирования природных и общественных явлений, систем и устройств. Постепенно в сферу систем компьютерной математики проникают средства реализации виртуальной реальности, искусственного разума и искусственного интеллекта.
Применение систем компьютерной математики нередко становится именно той «палочкой-выручалочкой», которая столь необходима всем, кто не имеет возможности и времени регулярно практиковаться в математических расчетах, но кто хоть иногда нуждается в их эффективном применении. Однако всегда надо помнить, что это применение должно быть грамотным, что предполагает достаточно глубокие знания основ математики .
Возможность применять математические методы и компьютерные технологии для решения задач естествознания, техники, экономики, социальных наук и управления, создавать математические, информационные, имитационные модели систем и процессов и использовать математические и компьютерные методы исследований при анализе современных естественнонаучных, экономических, социально-политических процессов вот чем уже занимается математика будущего — компьютерная математика.
А возможно, что будущее математики в том, о чём пишет в своей книге «Эволюция, нейронные сети, интеллект» В.Г. Редько. Автор занимается эволюционным моделированием интеллекта, то есть восстановлением хода эволюции интеллекта, что в свою очередь является своеобразным способом познать работу интеллекта в принципе. И уже одна вещь, упоминаемая там, заставляет задуматься: он приводит замечание, что условный рефлекс, вырабатываемый животными, по своему устройству напоминает правило вывода modus ponens в логике. Уже на этом моменте можно выдвинуть гипотезу: может стоит искать начала логики и математики в природе нашего мозга? Даже Кант сомневался в том, что мозг черпает законы Природы из наблюдений за ней, и, что скорее, он ей предписывает свои (т.е. своей работы) законы. Впрочем, дальше можно длинно и глубоко философствовать.
«. То обстоятельство, что мы вступили в век автоматизации процессов познания, позволяет нам считать, что пройден рубеж, который искусственно сдерживал границы математики, когда лозунг развития естествознания гласил мир устроен просто».
Математические описания различных систем и их взаимозависимостей еще ждут своих первооткрывателей. Философия исчезнет, как мертворожденный пережиток прошлого. Математика, с присущей ей абсолютной абстрактностью, будет единственным центром объединения всех наук. Математика коренным образом изменит представление человека об окружающем мире.
В завершение зададимся вопросом, какие еще кризисы могут ждать математику в обозримом будущем. Одна из возможностей состоит во вскрытии внутреннего противоречия в математических рассуждениях такой сложности, о которой никто и помыслить не может. Можно попытаться представить себе противоречие в результате ошибки, заложенной на уровне глубже человеческого понимания или превышающем вычислительные возможности мощнейших компьютеров. Кто-то скажет, что до этого еще далеко, однако с компьютерными шахматными программами нечто подобное уже происходит: иногда они делают такие ходы, что никто из гроссмейстеров не находит им логического объяснения. Компьютер, конечно, обоснует любой свой ход тем, что из миллиардов рассмотренных комбинаций именно он с наибольшей вероятностью приводит к успеху в партии. Однако это не означает, что выбранный компьютером ход действительно лучший, поскольку варианты просчитывались по алгоритмам, заданным человеком. Если нечто подобное произойдет, нам останется лишь признать нашу ограниченность как биологического вида и очертить пределы возможностей нашего интеллекта — и не только в математике.
В. М. Глушков Гносеологические основы математизации науки. — Киев : Наук. думка. -25 с. 184
В. П. Дьяконов, И. В. Абраменкова, А. А. Пеньков Новые информационные технологии: Учебное пособие. Часть 3. Основы математики и математическое моделирование. Смоленск: СГПУ, 2003. — 192 с. с рис.
Г.Г.Малинецкий Математические основы синергетики: Хаос, структуры, вычислительный эксперимент. М.: Либроком ,2009. – 132 с.
А. Пуанкаре. О науке. Наука и метод. М.: Наука. 1990
В. Г. Редько «Эволюция, нейронные сети, интеллект: Модели и концепции эволюционной кибернетики»
Только одно уравнение с пятью неизвестными
Mathcad дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно пятидесяти. В первой части этого раздела описаны процедуры решения систем уравнений. В заключительной части приведены примеры и проведено обсуждение некоторых часто встречающихся ошибок. Результатом решения системы будет численное значение искомого корня. Для символьного решения уравнений необходимо использовать блоки символьного решения уравнений. При символьном решении уравнений искомый корень выражается через другие переменные и константы.
Для решения системы уравнений выполните следующее:
- Задайте начальные приближения для всех неизвестных, входящих в систему уравнений. Mathcad решает уравнения при помощи итерационных методов. На основе начального приближения строится последовательность, сходящаяся к искомому решению.
- Напечатайте ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений. При печати слова Given можно использовать любой шрифт, прописные и строчные буквы. Убедитесь, что при этом Вы не находитесь в текстовой области или параграфе.
- Введите уравнения и неравенства в любом порядке ниже ключевого слова Given. Удостоверьтесь, что между левыми и правыми частями уравнений стоит символ =. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов ,
, и
.
- Введите любое выражение, которое включает функцию Find. При печати слова Find можно использовать шрифт любого размера, произвольный стиль, прописные и строчные буквы.
| Find(z1, z2, z3, . . . ) | Возвращает решение системы уравнений. Число аргументов должно быть равно числу неизвестных. |
Функция Find возвращает найденное решение следующим образом:
- Если функция Find имеет только один аргумент, то она возвращает решение уравнения, расположенного между ключевым словом Given и функцией Find.
- Если функция Find имеет более одного аргумента, то она возвращает ответ в виде вектора. Например, Find(z1, z2) возвращает вектор, содержащий значения z1 и z2 , являющиеся решением системы уравнений.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называются блоком решения уравнений.
На Рисунке 5 показан рабочий документ, который использует блок решения уравнений для решения одного уравнения с одним неизвестным. Так как имеется только одно уравнение, то только одно уравнение появляется между ключевым словом Given и формулой, включающей функцию Find. Так как уравнение имеет одно неизвестное, то функция Find имеет только один аргумент. Для решения одного уравнения с одним неизвестным можно также использовать функцию root, как показано ниже:
Рисунок 5: Блок решения уравнений для одного уравнения с одним неизвестным.
Между ключевым словом Given и функцией Find в блоке решения уравнений могут появляться выражения строго определенного типа. Ниже приведен список всех выражений, которые могут быть использованы в блоке решения уравнений. Использование других выражений не допускается. Эти выражения часто называются ограничениями. В таблице, приведенной ниже, через x и y обозначены вещественнозначные скалярные выражения, а через z и w обозначены любые скалярные выражения.
| Условие | Как ввести | Описание |
| w = z | [Ctrl] = | Булево равенство возвращает 1, если операнды равны; иначе 0 |
| x > y | > | Больше чем. |
| x |
Следующие выражения недопустимы внутри блока решения уравнений:
- Ограничения со знаком
.
- Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
- Неравенства вида a -15 .
Причиной появления этого сообщения об ошибке может быть следующее:
- Поставленная задача может не иметь решения.
- Для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число. Если решение задачи комплексное, то оно не будет найдено, если только в качестве начального приближения не взято также комплексное число. На Рисунке 11 приведен соответствующий пример.
- В процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Метод поиска решения, который используется в Mathcad, не позволяет в этом случае построить следующее приближение, которое бы уменьшало невязку. Для поиска искомого решения пробуйте использовать различные начальные приближения или добавьте ограничения на переменные в виде неравенств, чтобы обойти точку локального минимума.
- В процессе поиска решения получена точка, которая не является точкой локального минимума, но из которой метод минимизации не может определить дальнейшее направление движения. Метод преодоления этой проблемы — такой же, как для точки локального минимума: измените начальное приближение или добавьте ограничения в виде неравенств, чтобы миновать нежелательную точку остановки.
- Возможно, поставленная задача не может быть решена с заданной точностью. Если значение встроенной переменной TOL слишком мало, то Mathcad может достигнуть точки, находящейся достаточно близко к решению задачи, но уравнения и ограничения при этом не будут выполнены с точностью, задаваемой переменной TOL. Попробуйте увеличить значение TOL где-нибудь выше блока решения уравнений.
Что делать, когда имеется слишком мало ограничений
Если количество ограничений меньше, чем количество переменных, Mathcad вообще не может выполнить блок решения уравнений. Mathcad помечает в этом случае функцию Find сообщением об ошибке “слишком мало ограничений”.
Задача, аналогичная той, которая приведена на Рисунке 12, называется недоопределенной. Ограничений в ней меньше, чем переменных. Поэтому ограничения не содержат достаточной информации для поиска решения. Поскольку функция Find имеет пять аргументов, Mathcad определяет, что требуется решить два уравнения с пятью неизвестными. Вообще говоря, такая задача обычно имеет бесконечное число решений.
При использовании блока решения уравнений в Mathcad необходимо задать количество уравнений по крайней мере не меньшее, чем число искомых неизвестных. Если зафиксировать значения некоторых переменных, удастся решить уравнения относительно оставшихся переменных. На Рисунке 13 показано, как, зафиксировав часть переменных, решить недоопределенную задачу из Рисунка 12. Поскольку функция Find содержит только два аргумента, z и w, Mathcad определяет переменные x, y и v как имеющие фиксированные значения 10, 50 и 0 соответственно. Блок решения уравнений становится в этом случае корректно определенным, потому что теперь имеются только две неизвестных, z и w, и два уравнения.
Рисунок 12: Функция Find имеет пять аргументов, поэтому Mathcad определяет, что требуется решить два уравнения с пятью неизвестными.
Рисунок 13: Проблема может быть решена, если уменьшить количество аргументов функции Find.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Только одно уравнение с пятью неизвестными
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |

 , и
, и 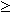 .
.
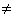 .
.
