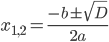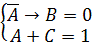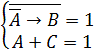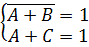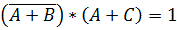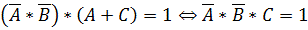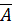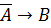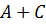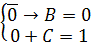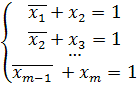Требуется найти все решения уравнения в с

Квадратное уравнение

Квадратное уравнение ax 2 + bx + c = 0 на C++ лучше всего решать с помощью формулы, содержащей дискриминант:

Разберем пример кода такой программы:

Данная программа учитывает все исходы при решении подобного уравнения.

Похожие записи:

Квадратное уравнение: 8 комментариев

Добрый день! А как быть со случаями, когда а == 0; b == 0 && c > 0; b == 0 && C !=0 и т.д.?

При a == 0 уравнение перестает называться квадратным. Проблемы также возникают, когда, например, пользователь ввел букву вместо числа. Такие случаи называются аномалиями.
Все аномалии рассмотреть нельзя. Если требуется, то можно, например, рассмотреть аномалию a == 0, добавив после 11-й строки:
if (a == 0)
<
cout

«Все аномалии рассмотреть нельзя.»
Сложно с Вами согласиться. Не такая уж это и нетривиальная задача для программиста — решить уравнение ax2 + bx + c = 0 на C++, учтя все возможные варианты а, b, c, в том числе и когда уравнение перестает быть квадратным и другие.
В противном случае код получается не универсальный, а только для некоторых случаев, когда переменные Вас «устраивают».
Согласитесь — это не решение задачи, а нахождение решения для группы частных случаев.

Нельзя. Будет всегда компьютер, бракованный, на котором программа не будет работать. На этом факте основано всё лицензирование программного обеспечения. Бракованный компьютер — тоже совокупность аномалий.

По квадратному уравнению имеет смысл рассматривать аномалии только, если от Вас это требуется в задании. И процесс такой длительный:
1. Рассматриваются случаи, когда пользователь ввел уравнение, не являющееся квадратным.
2. Рассматриваются случаи, когда пользователь ввел a,b,c, не являющиеся числами.
3. Рассматриваются случаи, когда пользователь, не умеет запускать программу, пишется инструкция.
4. Рассматриваются случаи, когда пользователь не умеет читать, пишется инструкция с картинками, часто с голосовым помощником.
5. Это именно программа, поэтому можно также составить инструкцию по компиляции, указать различные версии программы для разных стандартов языка.
.
Это все не моя выдумка, так делают, но только, если это действительно нужно.

Бывает другой случай, например, нужно сдать программу, решающую квадратное уравнение, преподавателю и вот здесь нужно сделать минимум, то, что написано в примере, а дальше, только если преподаватель просит.

Нет. Вы не правы.
Про аномалии — я вообще ничего не говорю. Я говорю только про задачу, которую озвучили Вы: решить ax2 + bx + c = 0. Другими словами — найти все возможные ответы при абсолютно любых значениях а, b и с. Без исключений. Не важно — квадратное будет уравнение или линейное, после того, как мы с консоли введем переменные. В этом весь смысл программирования. Сделать универсальное решение, которое будет работать всегда, при любых значениях переменных (аномалии, когда пользователю оторвало руки и он не может ввести переменные с консоли, истекая кровью, я тоже не рассматриваю).
Глупо, имея инструмент, который позволяет решить задачу, не решать её в любых, без исключения, случаях. А ограничивать себя только удобными случаями и тривиальными. Это не программирование получается, а ерунда какая-то, решение частных случаев. «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. »
Вот, корявый, конечно, не оптимальный, но работающий во всех случаях код:

#include
#include
using namespace std;

int main() <
double a, b, c;
cin >> a >> b >> c;
/*(D = b*b minus 4*a*c) — считаем дискриминант*/
double d = (b*b) — 4 * a * c;
double x1, x2, d1;
d1=sqrt(d);/*корень из дискриминанта — заготовка для решения решаемого квадратного уравнения*/
/*1. группируем все исключения — когда решение вообще или через дискриминант невозможно*/
/*2. в каждое исключение сливаем все условия и для этих условий пишем вывод*/
/*3. оставшиеся случаи решаем через дискриминант*/
if ((a==0 && b == 0 ) || ( b==0 && ((c> 0 && a>0) || (c

Про аномалии это я переделал. Лучше говорить аномалии, а не исключения.
Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.
Посмотрите математическую энциклопедию.

Ещё раз повторю: Вы не сможете сделать универсальное решение, которое будет работать всегда.

Ваше решение просто лучше моего, оно не работает, если вместо a, я ввожу rrr или другие символы.

Аномалии про оторванные руки и кровь тоже рассматривают, есть даже задачи и модели математические про ситуацию, когда 0 взял так и случайно стал 1 в памяти ЭВМ. Про глупость, ну а что, так и есть, глупость это нормально. Ваша программа умнее моей.

Это не ерунда, а программирование. Первый этап, который всегда должен происходить, это спецификация (уточнение) задачи. Пишется такая бумага, в которой как раз и есть «Сюда — смотри, сюда — не смотри, а здесь — рыбу заворачивали. «.

Вопрос у Вас фактически про спецификацию (уточнение). Те пять пунктов, которые я в предыдущем комментарии написал — совершенно адекватные требования преподавателя, заказчика, сайта с хранилищем программного обеспечения. Часто преподаватели говорят — составить отчёт с инструкциями даже по такой программе как решение квадратного уравнения, это нормально. Про оторванные руки я не писал как раз как про первоочередную задачу.

Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена. Если требуют уточнить, нужно уметь уточнять. Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.

Математической энциклопедии под рукой не нашлось.
«Лучше говорить аномалии, а не исключения.»
Не помню из курса алгебры (в рамках которой изучается решение квадратных уравнений) такого термина — аномалии, но допускаю, что Вы правы и такой математический термин существует и его можно применить к квадратному уравнению.
«Задачу читайте внимательно: квадратное уравнение. Подразумевается, что коэффициент a не равен 0.»
Прочитал внимательно. «ax2 + bx + c = 0» — где сказано, что а не равен нулю?
«Но по минимуму решение именно то, что я написал. Оно, бывает, проходит, при быстром ответе на вопрос экзамена.»
Когда я пытался пропихнуть код, который не учитывает исключений — не приняли, хотя вот текст моего задания:
«На вход вашей программы в стандартном потоке ввода подаются действительные коэффициенты A, B и C уравнения Ax² + Bx + C = 0. Выведите все его различные действительные корни в поток вывода в любом порядке, при этом разделяя корни пробелами. Гарантируется, что хотя бы один из коэффициентов уравнения не равен нулю.»
«Вы не сможете сделать универсальное решение, которое будет работать всегда.» и «Да и ещё раз замечу, Ваше решение умнее моего, но оно не универсально.»
Позвольте, Вы настаиваете, что невозможно написать код, который будет решать квадратное уравнение при любых действительных a, b и c? Как-то можете теоретически аргументировать? Пока что только не подкрепленные утверждения, не готов принимать их на веру.
При каких действительных значениях а, b и c мой, реально корявый, код не работает?

Страницы математических энциклопедий доступны через Яндекс. Только внимательнее, там есть поясняющие материалы в результатах поиска, не перепутайте.

Квадратное уравнение — алгебраическое уравнение 2-й степени. Общий вид К. у. ax^<2>+bx+c=0, a != 0.

Что такое аномалия?
В тестировании программного обеспечения под аномалией понимается результат, отличный от ожидаемого. Такое поведение может быть результатом документа а также представлений и опыта тестировщиков.

Аномалия может также относиться к проблеме удобства использования, поскольку тестовое программное обеспечение может вести себя в соответствии со спецификацией, но удобство его использования все же можно улучшить. Иногда аномалия также может быть названа дефектом / ошибкой.

Перед тем как разрабатывать программу проводят формальную спецификацию (уточнение) задания.

В информатике формальная спецификация — это математическое описание программной или аппаратной системы, которая может быть реализована в соответствии с этим описанием. Специфицируется, что должна делать система, но не то, как она должна это делать.

Если система огромная — длительное обсуждение, анализ и т.д. Для небольших программ, вот как решение квадратного уравнения, можно на бумаге составить. Вот на этой бумаге пишется задача, ИД — исходные данные, ВД — выходные данные, реакция на аномалии и т.д. В пункте реакция на аномалии рисуется таблица, по крайней мере с двумя столбцами: название аномалии, то что программа будет в этом случае делать.

У Вас в задании слова квадратное как раз нет и аккуратно написано, что подаются только действительные числа. Формальная спецификация выполнена в задании в основном.

Если будут вводить только действительные числа, можно написать работающий код. По такой формальной спецификации можно, я почти уверен, хотя доказательства корректности работы программы трудные.

Нельзя написать универсальное решение, без аномалий, на все случаи жизни. Тот же потенциальный пользователь программы решения квадратного уравнения, школьник, будет тыкать во всю клавиатуру, а не только в цифры.

Требуется найти все решения уравнения в с

Можно выделить различные способы решения систем логических уравнений. Это сведение к одному уравнению, построение таблицы истинности и декомпозиция.

Задача: Решить систему логических уравнений:

Рассмотрим метод сведения к одному уравнению. Данный метод предполагает преобразование логических уравнений, таким образом, чтобы правые их части были равны истинностному значению (то есть 1). Для этого применяют операцию логического отрицания. Затем, если в уравнениях есть сложные логические операции, заменяем их базовыми: «И», «ИЛИ», «НЕ». Следующим шагом объединяем уравнения в одно, равносильное системе, с помощью логической операции «И». После этого, следует сделать преобразования полученного уравнения на основе законов алгебры логики и получить конкретное решение системы.

Решение 1: Применяем инверсию к обеим частям первого уравнения:

Представим импликацию через базовые операции «ИЛИ», «НЕ»:

Поскольку левые части уравнений равны 1, можно объединить их с помощью операции “И” в одно уравнение, равносильное исходной системе:

Раскрываем первую скобку по закону де Моргана и преобразовываем полученный результат:

Полученное уравнение, имеет одно решение: A =0, B=0 и C=1.

Следующий способ – построение таблиц истинности. Поскольку логические величины имеют только два значения, можно просто перебрать все варианты и найти среди них те, при которых выполняется данная система уравнений. То есть, мы строим одну общую таблицу истинности для всех уравнений системы и находим строку с нужными значениями.

Решение 2: Составим таблицу истинности для системы:

Полужирным выделена строчка, для которой выполняются условия задачи. Таким образом, A=0, B=0 и C=1.

Способ декомпозиции. Идея состоит в том, чтобы зафиксировать значение одной из переменных (положить ее равной 0 или 1) и за счет этого упростить уравнения. Затем можно зафиксировать значение второй переменной и т.д.

Решение 3: Пусть A = 0, тогда:

Из первого уравнения получаем B =0, а из второго – С=1. Решение системы: A = 0, B = 0 и C = 1.

В ЕГЭ по информатике очень часто требуется определить количество решений системы логических уравнений, без нахождения самих решений, для этого тоже существуют определенные методы. Основной способ нахождения количества решений системы логических уравнений – замена переменных . Сначала необходимо максимально упростить каждое из уравнений на основе законов алгебры логики, а затем заменить сложные части уравнений новыми переменными и определить количество решений новой системы. Далее вернуться к замене и определить для нее количество решений.

Задача: Сколько решений имеет уравнение ( A → B ) + ( C → D ) = 1? Где A, B, C, D – логические переменные.

Решение: Введем новые переменные: X = A → B и Y = C → D . С учетом новых переменных уравнение запишется в виде: X + Y = 1.

Дизъюнкция верна в трех случаях: (0;1), (1;0) и (1;1), при этом X и Y является импликацией, то есть является истинной в трех случаях и ложной – в одном. Поэтому случай (0;1) будет соответствовать трем возможным сочетаниям параметров. Случай (1;1) – будет соответствовать девяти возможным сочетаниям параметров исходного уравнения. Значит, всего возможных решений данного уравнения 3+9=15.

Следующий способ определения количества решений системы логических уравнений – бинарное дерево. Рассмотрим данный метод на примере.

Задача: Сколько различных решений имеет система логических уравнений:

Приведенная система уравнений равносильна уравнению:

Предположим, что x ₁ – истинно, тогда из первого уравнения получаем, что x ₂ также истинно, из второго — x ₃=1, и так далее до x_m = 1. Значит набор (1; 1; …; 1) из m единиц является решением системы. Пусть теперь x ₁=0, тогда из первого уравнения имеем x ₂ =0 или x ₂ =1.

Когда x ₂ истинно получаем, что остальные переменные также истинны, то есть набор (0; 1; …; 1) является решением системы. При x ₂=0 получаем, что x ₃=0 или x ₃=, и так далее. Продолжая до последней переменной, получаем, что решениями уравнения являются следующие наборы переменных ( m +1 решение, в каждом решении по m значений переменных):

Такой подход хорошо иллюстрируется с помощью построения бинарного дерева. Количество возможных решений – количество различных ветвей построенного дерева. Легко заметить, что оно равно m +1.

Метод подсчёта количества решений

Линейные алгебраические уравнения — одни из самых простых уравнений, которые мы можем решить. Если в уравнении только одна переменная, решение тривиально, в то время как для системы линейных уравнений существует множество способов найти уникальные решения.

В этой статье нас интересует частный случай линейного уравнения с несколькими переменными. Хорошо известно, что подобное уравнение имеет бесконечное число решений. Мы наложим определённые ограничения и в значительной степени сократим количество решений.

Общая форма интересующего нас уравнения:

где n и m — положительные целые числа.

Наша задача — найти число решений этого уравнения, предполагая, что xᵢ являются целыми числами. Это предположение значительно снижает число решений заданного уравнения.

Нам нужен метод

Давайте начнём с частного случая общего уравнения:

Нетрудно найти все решения этого уравнения методом простого счёта. Решения заданы парами (x₁, x₂):

Мы видим, что уравнение имеет шесть решений. Также нетрудно предположить, что, если мы заменим правую часть определённым положительным целым числом m, решения будут выглядеть так:

и мы сможем подсчитать число решений — m+1.

Это было просто, верно?

Теперь возьмём немного более сложный вариант с тремя переменными, скажем:

С несколько большими усилиями, чем в предыдущем примере, находим решения в виде наборов из трёх чисел (x₁, x₂, x₃):

Число решений в этом случае равно 10.

Легко представить, что метод прямого счёта может стать очень утомительным для уравнения с большим количеством переменных. Он также становится утомительным, если целое число в правой части уравнения становится больше — например, если в правой части у нас будет 8, а не 3, решений будет уже 45. Разумеется, не хотелось бы искать все эти решения методом прямого счёта.

Значит, нужен эффективный метод.

Разрабатываем метод

Существует ещё один способ, которым можно решить предыдущие два уравнения. Давайте снова начнём с этого уравнения:

Одним из решений было (5, 0). Давайте преобразуем его в:

Мы разложили решение на нули и единицы, соответствующие каждому числу. Ненулевую часть (в данном случае 5) мы разложили на соответствующее число единиц, а ноль преобразовали в ноль. Таким же образом мы можем разложить и другое решение:

Мы поменяли прежнее расположение нуля, чтобы получить новое решение. Итак, два числа в парах (обозначенные красным и голубым) разделены нулём (чёрный) в разложенном виде. Таким же образом запишем оставшиеся решения:

Записав решения таким образом, видим закономерность. Кажется, все решения — это просто перестановки нулей и единиц. Вопрос о том, сколько существует решений, становится эквивалентным вопросу как много таких перестановок нулей и единиц может быть сделано, начиная с любой из конфигураций.

В данном случае у нас есть 6 местоположений в разложенной конфигурации для размещения нулей и единиц. Мы можем выбрать простейшее решение в качестве начальной конфигурации:

Теперь всё, что нам нужно найти, это общее число способов, которыми можно заполнить шесть местоположений пятью единицами и одним нулём.

Подобные задачи подсчёта мы можем решить различными способами, но наиболее эффективным будет способ, разработанный в такой области математики как комбинаторика, которая даёт нам формулу для числа способов перестановки r объектов в n местоположений:

где n! (читается как “n факториал”) определяется как произведение всех целых чисел от 1 до n, т.е. n! = 1 × 2 × 3 × ⋅ ⋅ ⋅ × n. Мы также определяем 0! = 1.

Эта формула обычно записывается в компактной форме как:

Теперь, возвращаясь к задаче, мы можем использовать эту формулу для нахождения числа способов перестановки пяти единиц в шести местоположениях:

Это то же самое число, что мы получили методом прямого счёта!

Выглядит многообещающе, поэтому давайте проверим, сможем ли мы найти таким способом число решений второго линейного уравнения:

Некоторые решения можно записать в разложенном виде:

В этот раз нам нужно заполнить тремя единицами и двумя нулями пять местоположений. Используя формулу мы можем найти число способов расположения чисел:

И опять то же число, что мы получили методом прямого счёта. Мы можем также найти число решений для нерешённого случая, где в правой части уравнения 8 вместо 3. Одним из решений будет:

а нам нужно найти число способов разместить 8 единиц в 10 местоположениях, и это будет:

как и утверждалось выше.

Если мы уверены в том, что этот метод работает для всех случаев, нам нужна общая формула. Напомним, что общее уравнение имеет вид:

Простейшее решение этого уравнения:

Поскольку существует n переменных, количество нулей в этом решении равно n-1. Таким образом, разложение выглядит так:

В разложенной конфигурации видим m и n-1 нулей (как утверждалось выше).

Следовательно, общее число местоположений, которые нужно заполнить, равно (m+n-1). Единственное, что остаётся — найти число способов, которыми можно заполнить m+n-1 местоположений m единиц, что определяется по формуле: