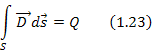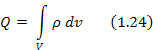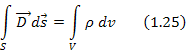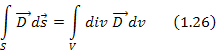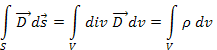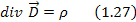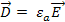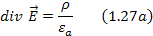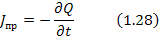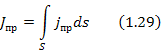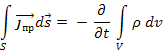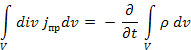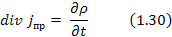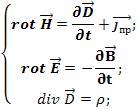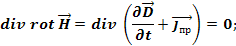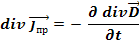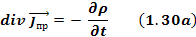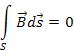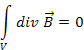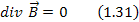Третье уравнение максвелла устанавливает связь

Третье уравнение Максвелла. Закон сохранения заряда.

Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.

Исходным для этого уравнения является уравнение Гаусса, которое говорит о том, что поток вектора 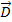через замкнутую поверхность S равен заряду Q, заключенному в данной поверхности:

где ρ – объемная плотность заряда.

Подставим 1.24 в 1.23, получим

Уравнение 1.25 есть третье уравнение Максвелла в интегральной форме.

Для того чтобы получить интегральную форму, воспользуемся теоремой Гаусса-Остроградского, которая устанавливает связь между объемным и поверхностным интегралом:

Применим 1.26 к левой части уравнения 1.25, получим

Данное равенство справедливо только в том случае, когда равны подынтегральные функции:

Уравнение 1.27 – третье уравнение Максвелла в интегральной форме.

и получим следующее уравнение

Для переменных полей заряды и токи связаны соотношением

где 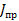— сила тока проводимости;

j_пр – плотность тока проводимости;

В итоге, с учетом этих соотношений получим

Воспользуемся теоремой Гаусса – Остроградского

Уравнение 1.30 выражает закон сохранения заряда:

Источник тока проводимости – это изменение заряда во времени.

Уравнение 1.30 также является необходимым дополнением к системе уравнений Максвелла, так как в этой системе необходимо было связать ρ и 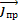. Это уравнение можно вывести, воспользовавшись уже имеющимися уравнениями Максвелла. Запишем систему уравнений Максвелла

Применим оператор div к первому уравнению Максвелла:

§1.5. Четвертое уравнение Максвелла.

Четвертое уравнение Максвелла устанавливает отсутствие магнитных зарядов и то, что магнитные силовые линии всегда замкнуты. В интегральном виде этот факт записывается в виде уравнения

Поток вектора магнитной индукции через замкнутую поверхность равен нулю, поскольку магнитных зарядов одного знака в природе не обнаружено.

Применяя теорему Гаусса – Остроградского

Уравнение 1.31 – это четвертое уравнение Максвелла в дифференциальной форме.

Дата добавления: 2016-01-29 ; просмотров: 2396 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Третье и четвертое уравнения Максвелла

Третье уравнение Максвелла является обобщением закона Гаусса на случай переменных процессов. Закон Гаусса связывает поток вектора электрического смещения через произвольную замкнутую поверхность S с зарядом Q, сосредоточенным внутри этой поверхности:

, (1.40)

где dS = n0dS; n0 – орт внешней нормали к поверхности S.

До Максвелла уравнение (1.40) рассматривалось только в применении к постоянным полям. Максвелл предположил, что оно справедливо и в случае переменных полей.

Заряд Q может быть произвольно распределен внутри поверхности S. Поэтому в общем случае

, (1.41)

где ρ – объемная плотность зарядов; V—объем, ограниченный поверхностью S. Объемная плотность зарядов

, (1.42)

где ΔQ – заряд, сосредоточенный в объеме ΔV. Размерность ρ – кулон на кубический метр (Кл/м3).

Подставляя (1.41) в (1.40), получаем

. (1.43)

Уравнение (1.43) обычно называют третьим уравнением Максвелла в интегральной форме. Для перехода к диффе­ренциальной форме преобразуем левую часть этого уравнения по теореме Остроградского-Гаусса (П. 19). В результате получим:

.

Это равенство должно выполняться при произвольном объеме V, что возможно только в том случае, если

Соотношение (1.44) принято называть третьим уравнением Максвелла. В декартовой системе координат оно записывается в виде

.

Из равенства (1.44) следует, что дивергенция вектора D отлична от нуля в тех точках пространства, где имеются свободные заряды. В этих точках линии вектора D имеют начало (исток) или конец (сток). Линии вектора D начинаются на поло­жительных зарядах и заканчиваются – на отрицательных.

В отличие от вектора D истоками (стоками) вектора Е могут быть как свободные, так и связанные заряды. Чтобы показать это, перепишем уравнение (1.44) для вектора Е. Подставляя соотношение (1.4) в (1.44), получаем εоdiv Е = ρ – div P. Второе слагаемое в правой части этого равенства имеет смысл объемной плотности зарядов , возникающих в результате неравномерной поляризации среды (такие заряды будем называть поляризационными):

divP = —. (1.45)

Поясним возникновение поляризационных зарядов на следующем примере. Пусть имеется поляризованная среда (рис. 1.8). Выделим мысленно внутри нее объем ΔV, ограниченный поверхностью ΔS. В результате поляризации в среде происходит смещение зарядов, связанных с молекулами вещества. Если объем ΔV мал, а поляризация неравномерная, то в объем ΔV с одной стороны может войти больше зарядов, чем выйдет с другой (на рис. 1.8 объем ΔVпоказан пунктиром). Подчеркнем, что поляризационные заряды являются «связанными» и возникают только под действием электрического поля. Знак минус в формуле (1.45) следует из определения вектора Р (см. 1.2.1).

Рис. 1.8. Поляризованная среда

Линии вектора Р начинаются на отрицательных зарядах и оканчиваются на положительных. С учетом формулы (1.45) приходим к соотношению εоdiv Е = ρ + ρp, из которого и следует сделанное выше утверждение, что истоками (стоками) линий вектора Е (силовых линий электрического поля) являются как свободные, так и связанные заряды.

Четвертое уравнение Максвелла в интегральной форме сов­падает с законом Гаусса для магнитного поля, который можно сформулировать следующим образом. Поток вектора В через любую замкнутую поверхность S равен нулю, т.е.

. (1.46)

Это означает, что не существует линий вектора В, которые только входят в замкнутую поверхность S (или, наоборот, только выходят из поверхности S): они всегда пронизывают ее (рис. 1.9).

Рис. 1.9. Линии вектора В, пронизывающие поверхность S

Уравнение (1.46) называют четвертым уравнением Максвелла в интегральной форме. К дифференциальной форме урав­нения (1.46) можно перейти с помощью теоремы Остроградского-Гаусса так же, как это было сделано в случае третьего уравнения Максвелла. В результате получим

Уравнение (1.47) представляет собой четвертое уравнение Макс­велла. Оно показывает, что в природе отсутствуют уединенные магнитные заряды одного знака. Из этого уравнения также следует, что линии вектора В (силовые линии магнитного поля) являются непрерывными.

Уравнения Максвелла

Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.

Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):

1. Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
2. В дальнейшем он вызывает появление магнитного поля.

Уравнения Максвелла в дифференциальной форме

Уравнение 1: Закон Гаусса или Теорема Гаусса

Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.

Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.

Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.

Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.

Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

Можно создать электрическое поле, изменив магнитное поле.

Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:

1. Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
2. Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
3. Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.

Уравнение 3: Закон Гаусса для магнетизма

Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.

Закон Гаусса для магнетизма утверждает (очень кратко):

1. Магнитных монополей не существует.
2. Расхождение полей B или H всегда равно нулю в любом объёме.
3. На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.

Уравнение 4: Закон Ампера

Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.

Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.

Уравнения Максвелла в интегральной и дифференциальной форме

Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.

Уравнение 1: Закон Гаусса (Теорема Гаусса)

Это же уравнение в интегральной форме:

Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).

Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.

Уравнение 3: Закон Гаусса для магнетизма

И это же уравнение в интегральной форме:

Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.

Уравнение 4: Закон Ампера

И это же уравнение в интегральной форме:

Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.