Третья краевая задача для уравнения теплопроводности как решить

ТРЕТЬЯ КРАЕВАЯ ЗАДАЧА ДЛЯ НАГРУЖЕННОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ С ДРОБНОЙ ПРОИЗВОДНОЙ КАПУТО Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Бештоков М.Х., Худалов М.З.

В последнее время при описании различных математических моделей физических процессов широко используется дробно-дифференциальное исчисление. В связи с этим большое внимание уделяется дифференциальным уравнениям с частными производными дробного порядка, которые являются обобщением уравнений с частными производными целочисленного порядка. При этом возможны различные постановки.Нагруженными дифференциальными уравнениями в литературе принято называть уравнения, содержащие значения решения или его производных на многообразиях меньшей размерности, чем размерность области определения искомой функции. В настоящее время широко используются численные методы решения нагруженных уравнений в частных производных целочисленного и дробного (пористые среды) порядков, поскольку аналитические методы решения оказываются невозможными.В данной работе исследуется начально-краевая задача для нагруженного дифференциального уравнения теплопроводности с дробной производной Капуто и условиями третьего рода. Для решения поставленной задачи в предположении существования точного решения в классе достаточно гладких функций методом энергетических неравенств получены априорные оценки в дифференциальной и разностной трактовках. Полученные неравенства означают единственность решения и непрерывная зависимость решения от входных данных задачи. В силу линейности рассматриваемой задачи эти неравенства позволяют утверждать сходимость приближенного решения к точному решению со скоростью равной порядку аппроксимации разностной схемы. Построен алгоритм численного решения поставленной задачи.

Похожие темы научных работ по математике , автор научной работы — Бештоков М.Х., Худалов М.З.

THE THIRD BOUNDARY VALUE PROBLEM FOR A LOADED THERMAL CONDUCTIVITY EQUATION WITH A FRACTIONAL CAPUTO DERIVATIVE

Recently, to describe various mathematical models of physical processes, fractional differential calculus has been widely used. In this regard, much attention is paid to partial differential equations of fractional order, which are a generalization of partial differential equations of integer order. In this case, various settings are possible.Loaded differential equations in the literature are called equations containing values of a solution or its derivatives on manifolds of lower dimension than the dimension of the definitional domain of the desired function. Currently, numerical methods for solving loaded partial differential equations of integer and fractional (porous media) orders are widely used, since analytical solving methods for solving are impossible.In the paper, we study the initial-boundary value problem for the loaded differential heat equation with a fractional Caputo derivative and conditions of the third kind. To solve the problem on the assumption that there is an exact solution in the class of sufficiently smooth functions by the method of energy inequalities, a priori estimates are obtained both in the differential and difference interpretations. The obtained inequalities mean the uniqueness of the solution and the continuous dependence of the solution on the input data of the problem. Due to the linearity of the problem under consideration, these inequalities allow us to state the convergence of the approximate solution to the exact solution at a rate equal to the approximation order of the difference scheme. An algorithm for the numerical solution of the problem is constructed.

Текст научной работы на тему «ТРЕТЬЯ КРАЕВАЯ ЗАДАЧА ДЛЯ НАГРУЖЕННОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ С ДРОБНОЙ ПРОИЗВОДНОЙ КАПУТО»

Математика и математическое моделирование. 2020. №3. С. 52-64.

© Бештоков М. X., Худалов М. 3., 2020.

Математика h Математическое

Сетевое научное издание

http://mathmelpub.ru ISSN 2412-5911

Третья краевая задача для нагруженного уравнения теплопроводности с дробной производной Капуто

Бештоков Μ. X.1’*, Худалов М. З.2

‘Институт прикладной математики и автоматизации КБНЦ РАН, Нальчик, Россия 2Северо-Осетинский государственный университет им. К.Л. Хетагурова, Владикавказ, Россия

Исследуется третья начально-краевая задача для нагруженного дифференциального уравнения теплопроводности с дробной производной Капуто. Для решения поставленной задачи в предположении существования точного решения в классе достаточно гладких функций методом энергетических неравенств получены априорные оценки в дифференциальной и разностной трактовках. Полученные неравенства означают единственность решения и непрерывная зависимость решения от входных данных задачи. В силу линейности рассматриваемой задачи эти неравенства позволяют утверждать сходимость приближенного решения к точному решению со скоростью O (h2 + τ2). Построен алгоритм численного решения поставленной задачи.

Ключевые слова: Нагруженное уравнение; краевая задача; априорная оценка; уравнение конвекции-диффузии; дифференциальное уравнение дробного порядка; дробная производная Капуто

Представлена в редакцию: 08.07.2020, исправлена: 07.08.2020.

В последнее время при описании различных математических моделей физических процессов широко используется дробно-дифференциальное исчисление [1,2, 3]. В связи с этим большое внимание уделяется дифференциальным уравнениям с частными производными дробного порядка, которые являются обобщением уравнений с частными производными целочисленного порядка. При этом возможны различные постановки. В настоящей статье рассматривается третья начально-краевая задача для нагруженного дифференциального уравнения теплопроводности дробного порядка.

Нагруженными дифференциальными уравнениями в литературе принято называть уравнения, содержащие значения решения или его производных на многообразиях меньшей размерности, чем размерность области определения искомой функции [4]. В работах A.M. Нахушева отмечается практическая и теоретическая важность исследований нагруженных

дифференциальных уравнений. Одним из методов приближенного решения краевых задач для дифференциальных уравнений является предложенный A.M. Нахушевым метод редукции интегро-дифференциальных уравнений к нагруженным дифференциальным уравнениям. В работе [4] впервые указана связь нелокальных задач с нагруженными уравнениями. Нелокальные задачи типа Бицадзе-Самарского для уравнений Лапласа и теплопроводности эквивалентно редуцированы к локальным задачам для нагруженных дифференциальных уравнений. Нагруженным дифференциальным уравнениям посвящены работы [4, 5, 6].

Численным методам решения локальных и нелокальных краевых задач для различных уравнений дробного порядка посвящены работы [7, 8, 9, 10, 11]. В работах [7, 8, 9] получены результаты, позволяющие, как и в классическом случае (а = 1), применять метод энергетических неравенств для нахождения априорных оценок краевых задач для уравнения дробного порядка в дифференциальной и разностной трактовках. В настоящее время широко используются численные методы решения нагруженных уравнений в частных производных целочисленного и дробного (пористые среды) порядков, поскольку аналитические методы решения оказываются невозможными.

Структура данной работы следующая. В первой части ставится третья начально-краевая задача для нагруженного дифференциального уравнения теплопроводности с дробной производной Капуто порядка а. Во второй части работы получена априорная оценка решения в дифференциальной форме. Из полученной оценки следует единственность и устойчивость решения по начальным данным и правой части. В третьей части рассматривается разностная схема, аппроксимирующая поставленную задачу. Получена априорная оценка в разностной форме. Доказана единственность, устойчивость и сходимость решения разностной задачи к решению дифференциальной задачи со скоростью равной порядку аппроксимации разностной схемы. В четвертой части построен алгоритм численного решения поставленной дифференциальной задачи.

краевую задачу для нагруженного дифференциального уравнения теплопроводности с дробной производной Капуто порядка а

1. Постановка третьей начально-краевой задачи

В прямоугольнике QT = <(x,t): 0 =

дробная производная в смысле Капуто порядка α, 0 0, i = 0, 1, 2.

В дальнейшем будем предполагать, что решение задачи (1)-(4) существует и обладает нужными по ходу изложения производными.

По ходу изложения будем также использовать Mi = const > 0, i = 1, 2, . зависящие только от входных данных рассматриваемой задачи.

2. Априорная оценка в дифференциальной форме

Теорема 1. Если k(x,t) Є C 1,0(QT), r(x,t), q(x,t), f (x,t) Є C(QT), u(x,t) Є C2,0(QT) П П C1,0(QT), d0>(x,t) Є C(QT) и выполнены условия (5), то для решения задачи (1)-(4) справедлива априорная оценка

I2 0 зависит от входных данных задачи (1)-(4); Cn,m(QT) — класс функций, имеющих непрерывные на QT производные до порядка n по x и m по t включительно.

Доказательство. Для получения априорной оценки решения задачи (1)-(4) в дифференциальной форме умножим уравнение (1) скалярно на u:

(д0tu, u) = ((kux)x, u + (rux, u) — (qu(xo,t), u^ + (f, u),

(a, b) = J abdx, ||a||2 = (a, a)

для заданных на [0, 1] функций a и b.

Преобразуем интегралы, входящие в тождество (6), используя неравенство Коши с ε, леммой 1 [7]:

(g0>, u = — udx uT(χ,τ)(t — τ) αάτ;

^Otu u) > 2(1, d0tu2) = 1 d0t\u\0;

((kux ) x , u^ J u( kux ) x dx ukux 0 C0\| ux II 0 ;

(rux, u) = J ruux dx — c2 J u2dx + ε J u2xdx — ε\ux\0 + M|||u||0;

— (qu(x0,t),u) = —J qu(x0,t)udx = —u(x0,t) qudx 0 зависит от входных данных задачи (1)-(4).

Из оценки (17) следуют единственность и устойчивость решения задачи (1)-(4) по правой части и начальным данным. Теорема доказана.

3. Устойчивость и сходимость разностной схемы

На равномерной сетке ωΗτ дифференциальной задаче (1)-(4) поставим в соответствие разностную схему порядка аппроксимации O(h2 + τ2):

ΔΜ,+σy=κ (aj)x,i + b-jajy%) +b+jal+ıy^i— dj (у^Ч- +У( ( і

(l + σ)2-α — (l — 1 + σ)

(l + σ)1-α + (l — 1 + σ)

aj = Ц^-о^^), bj = ,, ^ ·+σ,, dj = d(Xi,tj+σ),

^j = f (Xi,tj+σ), μı(tj+σ) = μι (tj+σ) + 0.5h 0. Отметим условия, которым удовлетворяют введенные переменные:

(s + σ) α > 0, xio 0.

Перепишем (18)-(21) в операторной форме:

Δ^+„ y = A(tj+„ )у(,) + Φ, (22)

y(x, 0) = uo(x), x є Wh,

A(tj+« )У( — O.bhdiiy^x- + уЦ_іж+)

АУ(,) = Ki(ayia))x,i + b ayia) + b+a(+1)yXj) — ^у^χίο + у(0+1х+),

(σ) — d(y(οσ)χ-ο + У(0+: j (σ) — (σ)

Д+ (σ) -KNaNyXjv — β2УІУ — 0.5hdN(Уі0 xİ0 + y(0+1x+0)

_Л , 0.5h|rо|λ-1 _Л , 0.5h|ri|λ-1 / , 0.5h|rw|λ-1

Теорема 2. Пусть выполнены условия (5). Тогда существует такое τ0, что при τ 0 не зависит от h и τ.

Доказательство. Умножим (22) скалярно на у(,):

Aft+σ)у(,), У( Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Δ0ί,+σ у, у — 1, Aj (у2)

Оценим первую сумму правой части:

затем оставшиеся три:

d(y’o?>xio + y(?>ıx+0t у(?>] — Й(У0?>)2 — β2(yN?>)2 Xİ0 + Лунxî+)2 +

(d, !/(?>f — Й(yi?>)2 — β(yN?>)2 Ш + M|| [у(?>]|0. (27) Учитывая (26), (27), из (25) находим

Ф, у(?>] = (φ, у(?>) + O.5hy0?>^ + 0.5hy(?>^+ = |φ у(?>] + μ^0?> + μ2yj?> ]|0 + Me(|[φ]|2 + μ12 + μ22 Принимая во внимание преобразования (24)-(29), из (23) находим:

Δοί,·+σ |[у]|2 + НуХст) ]|0 ]|2 + M^ |[φ]|0 + μ2 + μ2

Выбирая ε = , из (30) получаем:

г|[у]|0 + 11уХ^]|2 0 не зависит от h и τ. Теорема доказана.

Из оценки (32) следуют единственность и устойчивость решения по начальным данным и правой части.

Пусть n(x, t) —решение задачи (1)-(4), у(х, tj) = уі —решение разностной задачи (18)-(21). Для оценки точности разностной схемы (18)-(21) рассмотрим разность zj = уі — п\, где nj = u(xj,tj). Тогда, подставляя у = z + п в соотношения (18)-(21), получаем задачу для функции z:

Xі (ajzX?> )x,i + b- jajzx,i + aj+izX?> — (z(o?>X-0 + zi?+ıx+ ) + Ψ , (хУ) Є Wh,r,

κ0α1ζΧ?> = β z0?> + 0·5^Δ°^.+σ z0 + d0(z(0?>xİ0 + zi0+1xî0 ^ — ^1> κΝ aN ζΧσ)Ν = β z(?> + zN + (z(0?>x-0 + z(0?+ix0 )) — ^2

где Ψ = O(h2 + τ2), />1 = O(h2 + τ2), z>2 = O(h2 + τ2) — погрешности аппроксимации

дифференциальной задачи (1)-(4) разностной схемой (18)-(21) в классе решении u = u(x, t) задачи (1)-(4).

Применяя априорную оценку (32) к решению задачи (33)-(36), получаем неравенство

1 [zj+1] |0 0 не зависит от h и τ.

Из априорной оценки (37) следует сходимость решения разностной задачи (18)-(21) к решению дифференциальной задачи (1)-(4) в смысле нормы |[zj+1]|0 на каждом слое так, что существует такое τ0, что при τ Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Лекция 4. Вывод уравнения теплопроводности

При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.

Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:

Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.

Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.

Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q₁ = -kSU_x(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть U_x CpS∆x∆U = kSU_x(x + ∆х, t) ∆t — kSU_x(x, t)∆t.

Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:

Отсюда уравнение теплопроводности имеет вид

U_t = a 2 U_xx,
где 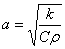— коэффициент температуропроводности.

В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности

Начальные условия и граничные условия.

Для уравнения теплопроводности задается только одно начальное условие U|_t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.

Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g₁(t) ≡ Т₁ и g₂(t) ≡ Т₂, где Т₁ и Т₂ — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т₁= Т₂ = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g₁(t) = g₂(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:

Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h₁ > 0 — коэффициент теплообмена с окружающей средой, g₁(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:

Аналогично получается условие (14) на правом конце стержня, только постоянная λ₂ может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.

Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h₁, очень большой.

Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.

Решение первой начально-краевой задачи для уравнения теплопроводности.

Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:

Найти решение уравнения

удолетворяющее граничным условиям

и начальному условию

Решим эту задачу методом Фурье.

Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).

Найдем частные производные:

Подставим эти производные в уравнение и разделим переменные:

По основной лемме получим

Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:

Шаг 2. Решим задачу Штурма-Лиувилля

Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.

Собственные значения равны

Собственные функции равны (См. решение задачи)

Шаг 3. Подставим собственные значения в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (15):

В силу линейности и однородности уравнения (15) их линейная комбинация

Шаг 5. Определим коэффициенты A_n в (19), используя начальное условие (17):

Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам

Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).

Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения U_t = a 2 U_xx. Оно будет иметь вид

где

Метод Фурье для уравнения теплопроводности

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Займемся решением первой смешанной задачи для уравнения теплопроводности: найти решение и(х, t) уравнения удовлетворяющее начальному условию и граничным условиям Начнем с простейшей задачи: найти решение u(x,t) однородного уравнения удовлетворяющее начальному условию и нулевым (однородным) граничным условиям Метод Фурье для уравнения теплопроводности.

Будем искать нетривиальные решения уравнения (4), удовлетворяющие граничным условиям (6), в виде Псдстаапя в форме (7) в уравнение (4), получим или откуда имеем два обыжювенных дифференциальных уравнения Чтобы получить нетривиальные решения и(х, *) вида (7), удовлетворяющие граничным условиям (6), необходимо найти нетривиальные решения уравнения (10), удовлетворяющие граничным условиям.

Таким образом, для определения фунмдои Х(х) мы приходим к задаче на собственные значения: найти те значения параметра А, при которых существуют нетривиальные решения задачи Эта задача была рассмотрена в предыдущей главе. Там было показано, что только при существуют нетривиальные решения При А = А„ общее решение уравнения (9) имеет вид удовлетворяют уравнению (4) и граничным условиям (6). Образуем формальный ряд.

Потребовав, чтобы функция и(х> t), определяемая формулой (12), удовлетворяла начальному условию , получим Ряд (13) представляет собой разложение заданной функции в ряд Фурье по синусам в интервале (О, I). Коэффициенты а„ разложения определяются по известным формулам Метод Фурье для уравнения теплопроводности Предположим, что Тогдаряд (13) с коэффициентами, определяемыми по формулам (14), будет сходиться к функции абсолютно и равномерно.

Так как при то ряд при также сходится абсолютно и равномерно.

Поэтому функция и(х, t) — сумма ряда (12) — непрерывна в области и удовлетворяет начальному и граничному условиям. Остается показать, что функция и(х, t) удовлетворяет уравнению (4) в области 0. Для этого достаточно показать, что ряды, полученные из (12) почленным дифференцированием по t один раз и почленным дифференцированием по х два раза, также абсолютно и равномерно сходятся при.

Но это следует из того, что при любом t > 0 если п достаточно велико. Единственность решения задачи (4)-(6) и непрерывная зависимость решения от начальной функции были уже установлены ранее. Таким образом, для t > 0 задача (4)-(6) поставлена корректно; напротив, для отрицательных t зада ча эта некорректна. Замечание.

В отличие отдомового уравнения уравнение неомметрично огноситн о времени t: если заменить t на -t, то получаем уравнение другого вида описывает необратимые процессы: Мы можем предсказать, каким станет данное и через промежуток времени данной t, но мы не можем с уверенностью сказать, какн м было это и за время t до рассматриваемого момента. Это раолич иемежду предсказание м и предысторией типично для параболического ура внения и не имеет места, например, для волнового уравн сния; в случае последнего заглянуть в прошлое так же легко, как и в будущее.

Возможно вам будут полезны данные страницы:

Пример:

Найти распределение температуры в однородном стерве длины ж, если начальная температура стержня и на концах стержня поддерживается нулевая температура. 4 Задача сводится к решению уравнения при начальном условии и граничных условиях Применяя метод Фурье, ищем нетривиальные решения уравнения (15), удовлетворяющие граничным условиям (17), в виде Подставляя u(x,t) в форме (18) в уравнение (15) и разделяя переменные, получим откуда Собственные значения задачи . собственные функции Хп(х) = мп пх.

При А = А„ общее решение уравнения (19) имеет вид Tn(t) = апе а п\ так что Решение задачи (15)—(17) ищем в виде ряда Потребовав выполнения начального условия (16), получим откуда . Поэтому решением исходной задачи будет фунхция 2. Рассмотрим теперь следующую задачу: найти решение гх(ж, t) неоднородного уравнения _ удовДстворя ющее начальному условию и однородным граничным услови м Предположим, что функци / непрерывна, имеет непрерывную производ-ную и при всех t > 0 выполняется условие .

Решение задач:

Решение задачи (1)-(3) будем искать в виде где определим как решение задачи а функци — как решение задачи Задача (8)—(10) рассмотрена в п. 1. Будем искать решение v(x, t) задачи (5)-(7) в виде ряда по собстве нным функциям < краевой задачи . Подсгааяяя t) в виде в уравнение (5), получим Разложим функцию /ОМ) в ряд Фурье по синусам, где Сравнивая два разложения (12) и (13) функции /(х, t) в ряд Фурье, получаем ! Пользуясь начальным условием для v(x, t).

Находим, что Решения уравнений (15) при начальных условиях (16) имеют вид: Подставляя найденные выражения для Tn(t) в ряд (11), получим решение Функция будет решением исходной задачи (1)-(3). 3. Рассмотрим задачу: найти в области решение уравнения при начальном условии и неоднородных граничных условиях Непосредственно метод Фурье неприменим из-за неоднородности условий (20).

Введем новую неизвестную функцию v(x, t), положив где Тогда решение задачи (18)—(20) сведется к решению задачи (1)-(3), рассмотренной в п. 2, для функции v(x, J). Упражнения 1. Задан бесконечный однородный стержень. Покажи те, что если начальная температура то влобой момент температура стержня 2. Ко|рцы стержня длиной ж поддерживаются при температуре, равной нулю. Начальная температура определяется формулой Определите температуру стержня для любого момента времени t > 0. 3.

Концы стержня длиной I поддерживаются при температуре, равной нулю. Начальная температура стержня определяется формулой Определите температуру стержня для любого момента времени t > 0. 4. Концы стержня длиной I поддерживаются при температуре, равной нулю. Начальное распределение температуры Определите температуру стержня для любого момента времени t > 0. Ответы

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.