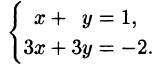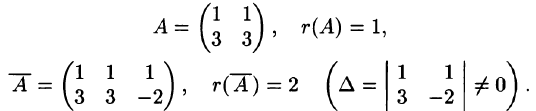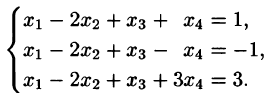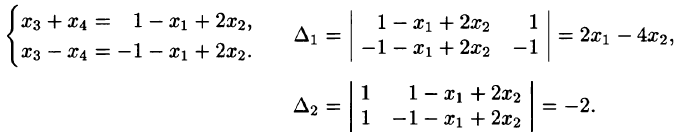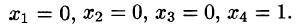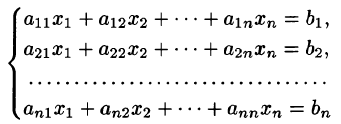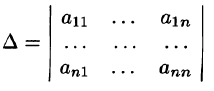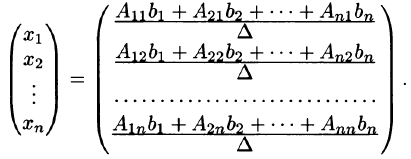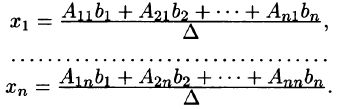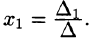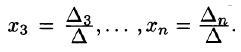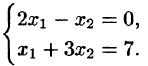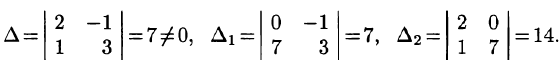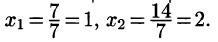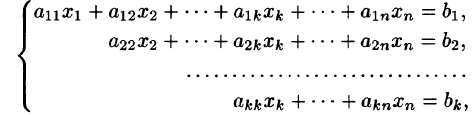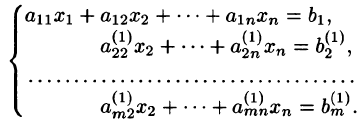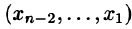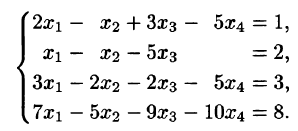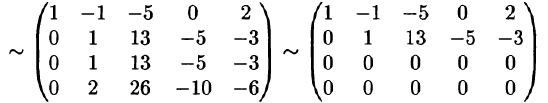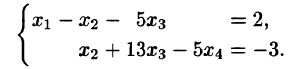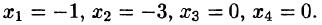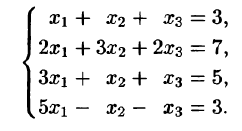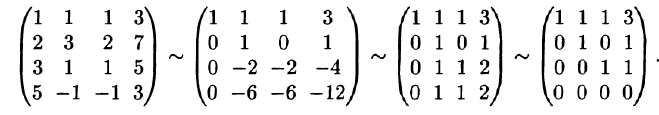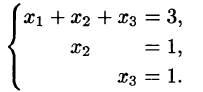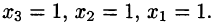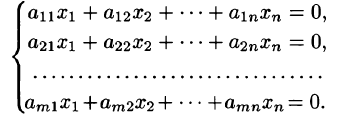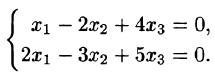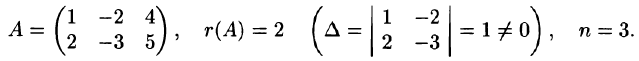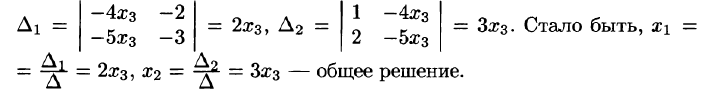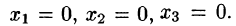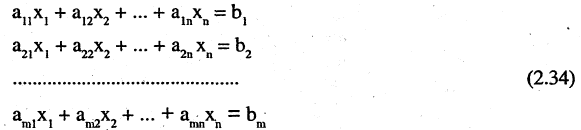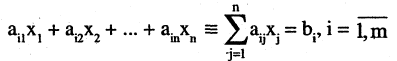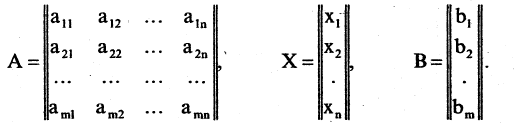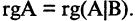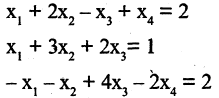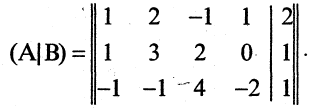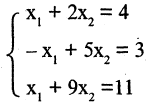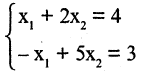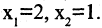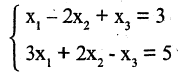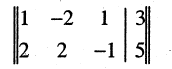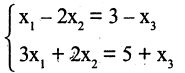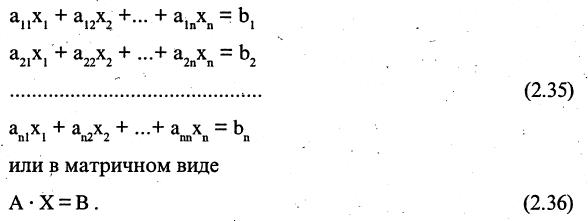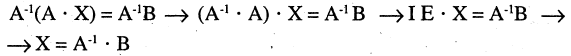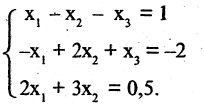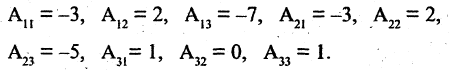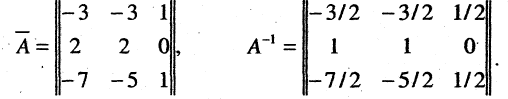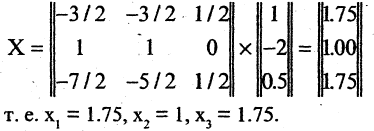Системы линейных уравнений в математике с примерами решения и образцами выполнения
Уравнения первой степени с двумя и тремя неизвестными изучают в восьмилетней школе. Как показано в курсе геометрии, уравнение первой степени с двумя переменными Ах + Ву = С задает прямую линию. Поэтому принято называть уравнение первой степени линейным. Например, линейное уравнение относительно неизвестных х, у, z, . . . , и может быть сведено к виду
Числа А, В, С . . . , D называют коэффициентами при неизвестных, а Е — свободным членом уравнения.
Мы рассмотрим системы линейных уравнений со многими неизвестными. Для таких систем становится неудобным обозначать неизвестные через х, у, z, . . . , u. Значительно удобнее перенумеровать неизвестные и обозначить их 
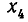
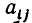
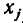
В восьмилетней школе мы рассматривали лишь системы уравнений, для которых число уравнений равнялось числу неизвестных. Сейчас мы будем изучать системы, состоящие из m линейных уравнений с n неизвестными. Такие системы записываются следующим образом:
Например, для системы
имеем
Нашей задачей является найти все решения системы линейных уравнений (2) или показать, что эта система не имеет решений, что она несовместна. Мы покажем ниже, что возможны три случая: а) система (2) несовместна, б) система (2) имеет единственное решение, в) система (2) имеет бесконечное множество решений.
Теоремы о равносильности систем линейных уравнений
Пусть дана система линейных уравнений:
Умножим i-е уравнение этой системы на любое число 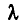
Из следствия к теореме 4 п. 7 вытекает, что если заменить j-е уравнение системы (1) уравнением (2), то получится система уравнений, равносильная данной.
Повторно применяя это утверждение, приходим к следующей теореме.
Теорема:
Если к любому уравнению системы (1) прибавить сумму остальных уравнений, взятых с любыми коэффициентами, то получится система линейных уравнений, равносильная исходной.
Отметим еще следующие простые теоремы.
Теорема:
Если среди уравнений системы есть уравнение вида
то после отбрасывания этого уравнения получается система, равносильная исходной.
Эта теорема вытекает из того, что любой набор чисел 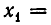
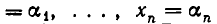
Теорема:
Если среди уравнений системы есть уравнение вида
где 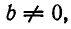
Эта теорема вытекает из того, что ни один набор чисел 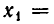
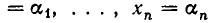
Пример решения системы линейных уравнений методом Гаусса
В восьмилетней школе системы линейных уравнений (с двумя или тремя неизвестными) решаются или методом подстановки, или методом алгебраического сложения. Сейчас мы изложим метод Гаусса, очень близкий к методу алгебраического сложения, но отличающийся от него большей систематичностью. Покажем сначала этот метод на следующем примере.
Пусть надо решить систему уравнений:
Умножим первое уравнение системы на —2 и прибавим его ко второму, потом умножим первое уравнение на —5 и прибавим к третьему, наконец, умножим первое уравнение на —1 и прибавим к четвертому. Система уравнений примет вид:
Мы видим, что в результате преобразований неизвестное 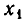
Теперь преобразуем тем же путем три последних уравнения. Умножим второе уравнение на —2 и прибавим к третьему, а по том умножим второе уравнение на —1 и прибавим к четвертому.
Наконец, умножим третье уравнение на — 1 и прибавим к четвертому. В результате получаем систему:
Системы такого вида называют треугольными.
Из теоремы 5 вытекает, что треугольная система (4) равносильна. исходной системе (1). Треугольную систему уравнений легко решить. Из последнего уравнения находим, что 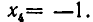
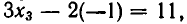
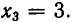
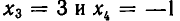
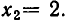
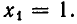
Метод Гаусса (приведение системы к обобщенно-треугольному виду).
Рассмотрим теперь решение методом Гаусса систем линейных уравнений общего вида. Пусть задана система уравнений:
Если 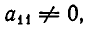
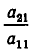
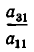
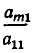
Здесь для краткости введены следующие обозначения:
Таким образом, если 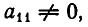
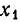
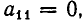
а) Все коэффициенты и свободный член первого уравнения равны нулю: 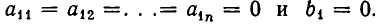
В силу теоремы 6, п. 2, мы можем его отбросить, не меняя множества решений системы (1).
б) Все коэффициенты 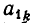
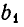
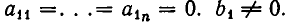
и по теореме 7, п. 2, система несовместна.
в) 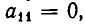

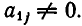
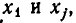
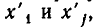
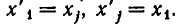
неравносильны). Но переход от одной системы уравнений к другой сводится к перестановке неизвестных. После изменения номеров у неизвестных место коэффициента 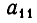
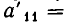
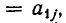
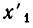
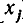
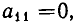
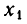
Вернемся теперь к системе уравнений (2). Если 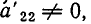
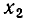
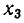
а) В ходе решения мы получаем уравнение вида
где 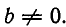
б) При решении системы уравнений вида (3) не получается. Тогда через конечное число шагов (не более чем через т — 1 шаг) мы получим систему вида:
где диагональные коэффициенты 
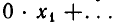
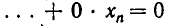
Систему уравнений (4) мы будем называть обобщенно-треугольной системой уравнений. Таким образом, метод Гаусса позволяет либо установить, что данная система линейных уравнений несовместна, либо заменить ее равносильной обобщенно-треугольной системой.
Назовем число r уравнений в системе (4) рангом заданной системы уравнений. На первый взгляд может показаться, что ранг заданной системы зависит не только от этой системы, но и от того, каким путем ее приводили к обобщенно-треугольной форме (в каком порядке записывали уравнения, как нумеровали неизвестные и т. д.). Оказывается, это не так: при любом способе приведения за данной системы линейных уравнений к равносильной ей обобщенно-треугольной системе уравнений получается система, состоящая из одного и того же числа уравнений. Доказательство этого утверждения довольно сложно, и мы его опускаем. Отметим, что ранг r системы не больше числа m уравнений этой системы.
Решение обобщенно-треугольной системы линейных уравнений
Покажем теперь, что любая обобщенно-треугольная система уравнений совместна, и выясним, когда она имеет единственное решение. Сначала разберем случай, когда ранг системы r равен числу неизвестных n, r =n. Тогда система (4), п. 4, имеет вид:
то есть является треугольной. При этом 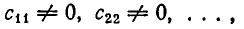
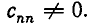
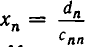
После этого последовательно определяем 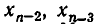
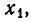
Перенесем слагаемые, содержащие неизвестные 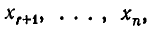
Эта система имеет бесконечное множество решений. В самом деле, дадим неизвестным 
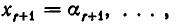
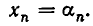

Решая ее, получим искомые значения для 

Например, решим систему уравнений:
Она приводится к обобщенно-треугольной системе:
Значит, ее ранг равен двум. Перенося слагаемые, содержащие 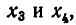
Из этой системы находим:
Любое решение уравнения (5) получится, если придать некоторые значения неизвестным 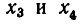
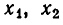
Подведем итоги исследования:
Всякая система линейных уравнений либо не имеет решений (несовместна), либо имеет единственное решение, либо бесконечное множество решений.
Первый случай будет, если при решении системы методом Гаусса мы придем к уравнению вида
где 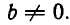
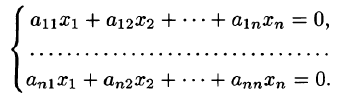
6. Системы однородных линейных уравнений. Линейное уравнение, свободный член которого равен нулю, называется однородным. Оно имеет вид
Мы рассмотрим сейчас систему таких уравнений:
Система однородных линейных уравнений заведомо разрешима, поскольку ей удовлетворяет решение 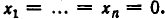
Если ранг системы однородных линейных уравнений равен числу неизвестных, r = n, то, как мы знаем, система имеет единственное решение. Так как одно решение, а именно нулевое, мы уже знаем, то ненулевых решений система не имеет. Если же ранг системы меньше числа неизвестных, то система имеет бесконечное множество решений. Поэтому у нее, кроме нулевого будут и ненулевые решения. Мы доказали, таким образом, следующую теорему.
Теорема:
Для того чтобы система однородных линейных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг r этой системы был меньше числа неизвестных n.
Так как ранг системы заведомо меньше числа уравнений исходной системы, то отсюда получаем
Следствие:
Для того чтобы система m однородных линейных уравнений с n неизвестными имела ненулевое решение, достаточно, чтобы число уравнений было меньше числа неизвестных, m
Применяя метод Гаусса, приходим к системе уравнений:
Ее можно записать так:
Отсюда находим, что 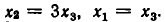
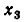
Симметрические многочлены и их приложения к решению систем уравнений
Симметрические многочлены от двух переменных: При решении многих задач геометрии весьма полезным оказывается использование симметрии и ее свойств. В алгебре также существенную помощь в решении задач оказывает учет симметричности тех или иных алгебраических выражений. Разумеется, понятия симметрии в геометрии и в алгебре имеют различный смысл. В алгебре оно означает, что данное выражение не меняется при перестановке входящих в него букв. Например, выражение 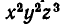
Мы изучим сейчас симметрические многочлены от двух переменных, то есть такие многочлены f(х, у), что f(х, у) = f(у, x).
Например, многочлен 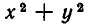
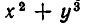
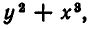
Простейшими симметрическими многочленами от двух переменных х и у являются сумма и произведение этих переменных, то есть х+у и ху. Введем для этих многочленов специальные обо значения:
Симметрическими являются многочлены вида 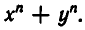
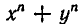
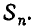
Выражение степенных сумм через
Рассмотрим первые три степенные суммы 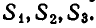
Докажем, что это утверждение верно для любых степенных сумм.
Теорема:
Любая степенная сумма 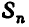
Иными словами, для любого n существует такой многочлен 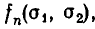
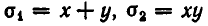
Доказательство:
Применим для доказательства метод математической индукции. При n = 1 наше утверждение справедливо, поскольку 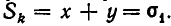
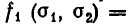
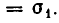
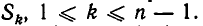
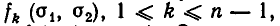
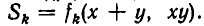
Это равенство можно записать так:
то получаем, что
Мы предположили, что 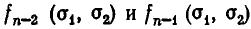
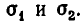
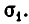
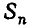
Итак, доказываемое утверждение верно при n = 1 и из его справедливости при 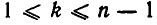
Примеры:
1) Выразим через 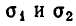
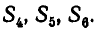
Точно так же находим:
Основная теорема о симметрических многочленах от двух переменных
Теорема 1, п. 7, является частным случаем следующего общего утверждения.
Теорема:
Для любого симметрического многочлена F(х, у) существует такой (вообще говоря, несимметрический) многочлен 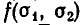
Доказательство. Пусть F(х, у) — симметрический многочлен. Возьмем какой-нибудь из его членов 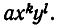
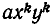
Если же 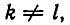
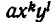
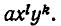
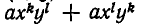
Мы уже умеем выражать 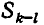
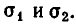
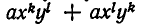
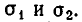
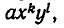
Пример:
Выразить через 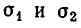
Применяя формулу для 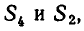
Системы симметрических алгебраических уравнений
Мы уже говорили, что иногда удается упростить решение системы алгебраических уравнений, удачно введя новые неизвестные. Этот путь решения приводит к успеху, если заданная система уравнений симметрична, то есть имеет вид:
где Р(х, у) и Q (х, у) — симметрические многочлены от х и у.
Простейшей системой такого вида является:
Будем рассматривать числа х и у как корни некоторого квадратного уравнения. Тогда по теореме Виета коэффициент при первой степени неизвестного в этом уравнении равен —а, а свободный член равен b. Иными словами, квадратное уравнение с корнями х и у имеет вид:
Пусть корни этого уравнения 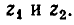
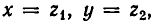
Рассмотрим теперь более сложную систему:
Так как левые части обоих уравнений симметрично зависят от х и у, то введем вместо х и у новые неизвестные
Выразим через эти неизвестные левые части уравнений (3). Мы получим:
Таким образом, заданная система свелась к следующей:
Сложив эти уравнения, получим квадратное уравнение относительно
Из него следует, что 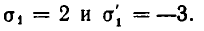
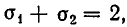
Поскольку 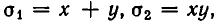
Решая первую систему, находим два решения:
Вторая система действительных решений не имеет. Точно так же решается система уравнений:
то данную систему можно записать в виде:
Подставляя во второе уравнение значение о 4 = 5, получаем квадратное уравнение:
Из него находим, что 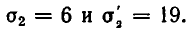
Решая первую систему, получаем:
Вторая же система не имеет действительных решений.
Выгода введения неизвестных 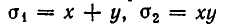
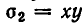
Применение симметрических многочленов к решению иррациональных уравнений
Решение некоторых иррациональных уравнений можно свести к решению систем симметрических алгебраических уравнений. Рассмотрим иррациональное уравнение
Здесь выгодно ввести два вспомогательных неизвестных, положив
Тогда заданное уравнение примет вид: u + v = 5. Кроме того, имеем: 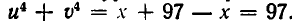
Введем новые неизвестные:
Так как 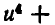
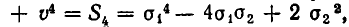
Подставим во второе уравнение значение 
Решая его, находим 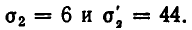
Первая из этих систем имеет два решения: 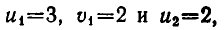
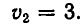
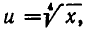
Вторая система не имеет действительных корней.
Итак, заданное уравнение имеет лишь два корня: 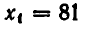
Дополнение к решению систем линейных уравнений


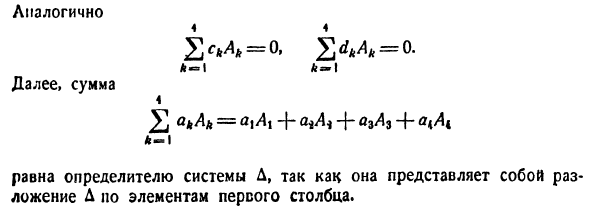









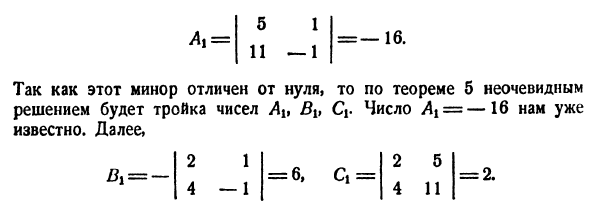

Системы линейных уравнений — решение заданий и задач по всем темам с вычислением
Метод Жордана-Гаусса
1°. Система из то линейных уравнений с п неизвестными в общем случае записывается так:
Коэффициенты 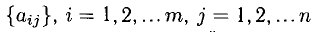
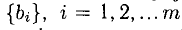
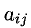
Решить систему (1) — значит найти все ее решения, т.е. все такие наборы чисел 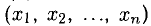
Система (1) называется:
— совместной, если она имеет хотя бы одно решение;
— определенно совместной, если она имеет только одно решение;
— неопределенно совместной, если она имеет более одного решения;
— несовместной, если она не имеет ни одного решения.
2°. Две системы называются равносильными, если они имеют одинаковые решения или обе несовместны.
Переход от одной системы к равносильной осуществляется при помощи множества элементарных преобразований:
— умножение обеих частей любого уравнения на отличное от нуля число;
— прибавление к одному из уравнений произвольного другого, умноженного на любое число;
— удаление (вычеркивание) из системы тривиального уравнения
— если в системе имеются два или более уравнений с пропорциональными коэффициентами, то сохранить нужно только одно из них.
Уравнение 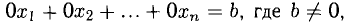
3°. Один шаг метода Жордана-Гаусса состоит в приведении системы (1) к виду
в котором одна неизвестная 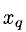
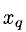
Для того, чтобы получить систему (2), требуется следующее:
1) коэффициент 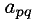
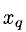
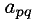
2) р-е уравнение надо разделить на 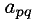
3) для получения нулевых коэффициентов при 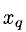
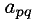
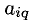
Тогда все остальные коэффициенты 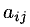
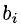
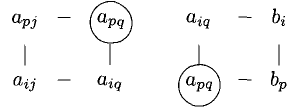
Эти формулы будем называть формулами Жордана-Гаусса. Расчет по ним удобно выполнять, пользуясь мнемоническим правилом прямоугольника, наглядно показанным на следующих диаграммах:
Смысл диаграмм следующий: новый коэффициент 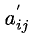
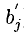
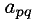
4°. На втором шаге сохраним с коэффициентом 1 другую неизвестную в другом уравнении, исключая из остальных.
Через 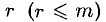
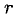
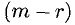
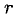
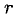
Если 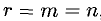
Если 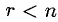
Заметим, что «общее» решение определяется неоднозначно, оно зависит от того, какие неизвестные являются свободными (независимыми, произвольными), а какие — зависимыми (базисными).
5°. Метод Жордана-Гаусса удобно реализовать в виде таблицы, которую назовем таблицей Гаусса. Каждый ее блок содержит результат одного преобразования или одну итерацию. Столбец блока таблицы, состоящий из нулей и одной единицы, будем называть единичным столбцом. Цель преобразований Жордана-Гаусса — получить 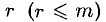
Примеры с решениями
Пример:
Решить линейную систему
1. Выполним первую итерацию, т.е. получим первый единичный столбец, выбирая в качестве ведущего коэффициента 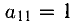
Решение:
Первый блок таблицы Гаусса данной системы имеет вид («св. ч.» означает «свободные члены» уравнений системы, вертикальная черта соответствует знакам равенства):
1) первую строку сохраняем (переписываем);
2) первую строку, умноженную на 2, прибавим 0 ко второй;
3) первую строку, умноженную на -2, прибавим к третьей;
4) первую строку прибавим к четвертой.
Получаем второй блок таблицы:
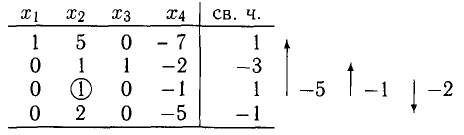
2. Приведем к единичному третий столбец, в нем уже имеется один нуль. Ведущий коэффициент 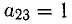
1) вторую строку, умноженную на 3, прибавим к первой и запишем вместо первой строки;
2) перепишем вторую строку без изменения;
3) вторую строку, умноженную на —1, прибавим к третьей;
4) четвертую строку перепишем без изменения.
Эти действия выражаются числами и стрелками, показанными справа от второго блока таблицы. Третий блок таблицы имеет вид:
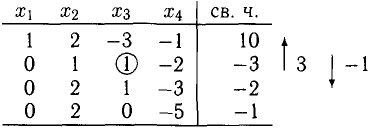
3. Следующая итерация заключается в получении третьего единичного столбца. Для этого примем в качестве ведущего коэффициента 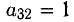
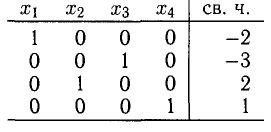
4. Наконец, последнюю итерацию выполним, выбирая в качестве ведущего коэффициента 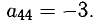
5. После четырех итераций получили таблицу, соответствующую системе, разрешенной относительно всех неизвестных 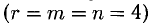
Запишем это также в виде: X = (-2,2,-3,1). Система определенно совместна.
Примечание:
Подставьте эти значения неизвестных в данную систему и убедитесь, что получаются верные числовые равенства.
Пример:
Решить линейную систему
Решение:
Каждый раз в качестве ведущего будем принимать простейший коэффициент, т.е. либо 1, либо — 1. Подчеркнем, что цель преобразований заключается в получении нулей в ведущем столбце. Как получить нулевые коэффициенты в единичном столбце, видно из решения примера 1. Для этого ведущую строку надо умножить на надлежащие числа (иногда на 1 или -1) и прибавить к остальным строкам, не содержащим 0 в этом ведущем столбце. Поэтому ограничимся выделением в каждом блоке ведущего коэффициента, не комментируя сами преобразования и не указывая соответствующие числа со стрелками. Результаты вычислений поместим в единую таблицу Гаусса, которая имеет следующий вид:
Последние две строки удалены как нулевые (они соответствуют тривиальным уравнениям).
Из последнего блока таблицы получаем систему
выражающую «почти» общее решение исходной системы. Смысл слова «почти» заключается в неравноправном участии неизвестных.
Положим 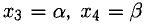
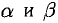
представляет общее решение системы в параметрическом виде. Все неизвестные выражены (равноправно) через два параметра
Решения, получаемые из общего при фиксированных значениях параметров 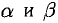
Например, при 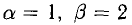
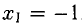
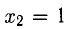
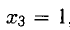
При 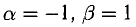
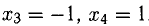
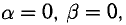
Ответ запишем так:
Пример:
Решить систему уравнений
Решение:
Вместо таблицы Гаусса будем использовать другую, более компактную интерпретацию ее блоков. Вертикальная черта в блоках соответствует знакам равенства в уравнениях системы. Знак
(читается «тильда») между двумя соседними блоками означает, что системы, соответствующие этим блокам, равносильны. Имеем:
единичный столбец второго блока получен в результате умножения первой строки на —3, —3, -1, -4 и последующего прибавления ко второй, третьей, четвертой и пятой строкам соответственно; во втором блоке произвели почленное деление четвертой и пятой строк на 3 и —3, т. е. сокращение уравнений
Вторая и третья строки четвертого блока отброшены как пропорциональные пятой. Заметим, что выделение ведущего (разрешающего) элемента однозначно определяет действия по обнулению элементов ведущего столбца, поэтому мы отказались от применения чисел и стрелок, обозначающих действия над строками блока.
Последний блок изображает систему, состоящую из трех уравнений 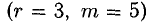
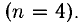
Положим 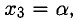
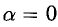
Заметим, что переменную 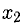
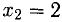
Пример:
Решить систему уравнений
Решение:
В предыдущих примерах преобразования Жордана-Гаусса свелись к действиям над уравнениями системы, или строками таблицы, потому что все ведущие коэффициенты были равны 1. Если же ведущие коэффициенты отличны от 1, то действия над строками могут вызывать затруднения, и в таких случаях следует пользоваться формулами преобразования Жордана-Гаусса, т.е. правилом прямоугольника.
С целью экономии места решение этой системы приведем также в блоковой записи:
(последняя строка пропорциональна первой, поэтому она удалена). Подчеркнем, что цель наших преобразований состоит в получении единичных столбцов.
Приведем примеры применения правила прямоугольника в третьем блоке. При этом одна из вершин каждого прямоугольника должна совпасть с ведущим элементом 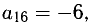
Из последнего блока получаем общее решение системы в базисе
При 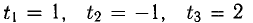
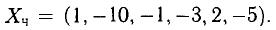
Примечание:
Метод Гаусса (усеченный метод Жордана-Гаусса) допускает получение в очередном блоке таблицы Гаусса столбца, отличного от единичного, т.е. неизвестную не обязательно исключать из всех уравнений, кроме одного. В этом случае говорят о приведении системы уравнений к ступенчатому виду. Это важно в смысле экономии времени, когда коэффициенты системы «неудобные», особенно, если система окажется неразрешимой.
Пример:
Решить систему уравнений
Решение:
Нули в столбцах будем получать только под диагональю соответствующей матрицы.
Последняя строка выражает противоречивое уравнение — система несовместна.
Метод Крамера
1°. Если в системе (1) число уравнений равно числу неизвестных
и система имеет единственное решение, то оно может быть найдено при помощи формул Крамера
где 
а 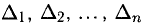


Сначала рассмотрим определение и вычисление определителей различных порядков n.
2°. Если 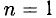

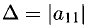
Если 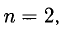
3°. Для указания способа вычисления определителя третьего и более высоких порядков (см. (5)) введем необходимые понятия минора и алгебраического дополнения.
Минором 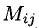
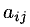
Величина 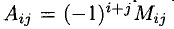
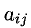
Например, для определителя третьего порядка
4°. Способ вычисления определителя порядка п выражается следующей теоремой о разложении определителя по строке или столбцу (под линией понимается строка или столбец).
Теорема:
Определитель порядка 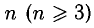
Теорема:
Сумма произведений элементов какой-либо линии на алгебраические дополнения другой параллельной линии равна нулю.
Например, для определителя из п. 3° по первой строке. Получаем
воспользуемся разложением
5°. С теоретической точки зрения при вычислении определителя безразлично, какую строку или какой столбец взять для разложения. С практической точки зрения лучше брать ту линию, которая содержит нулевые элементы, и чем их больше, тем лучше.
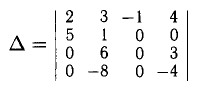
Например, для вычисления определителя четвертого порядка
лучше брать сначала разложение по третьему столбцу:
Этот определитель третьего порядка разложим по первому столбцу:
6°. При вычислении определителей порядка 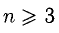
1) При транспонировании (так называется действие замены строк столбцами и столбцов строками с сохранением их порядка) значение определителя не изменяется. Таким образом, строки и столбцы определителя равноправны.
2) Если определитель содержит нулевую линию (т. е. состоящую из одних нулей) или две параллельные пропорциональные линии, то его значение равно 0.
3) При умножении любой линии на произвольное число значение определителя умножается на это число. Иными словами, общий множитель элементов некоторой линии можно вывести за знак определителя.
4) При перестановке двух параллельных линий значение определителя изменяется на противоположное (определитель меняет знак).
5) Значение определителя не изменится, если к элементам произвольной линии прибавить соответственные элементы любой другой параллельной линии, умноженные на одно и то же число.
7°. Теорема 3 (Крамера). 1) Если для квадратной системы (3) 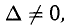
2) Если 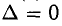
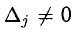
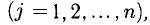
3) Если 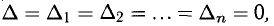
Примечание. В случае 3) решить систему можно методом Жор-дана-Гаусса. Вместе с тем ее можно решить также методом определителей. Только формулы Крамера применимы не к системе (3), а к модифицированной системе (см. пример 4 ниже).
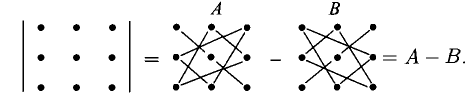
8°. Определители третьего порядка встречаются чаще. Поэтому для них (и только) покажем два простых правила вычисления.
а) Правило параллельных линий заключается в следующем. К исходному определителю приписываем два первых столбца и составляем две группы произведений, как указано на диаграмме:
б) Правило Саррюса (треугольников) заключается в том, что множители произведений, составляющих суммы А и В, образуют фигуры, показанные на следующей диаграмме:
(показана только фигура А)
Примеры с решениями
Пример:
Решить систему уравнений
Решение:
По формулам Крамера: 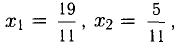
Пример:
Решение:
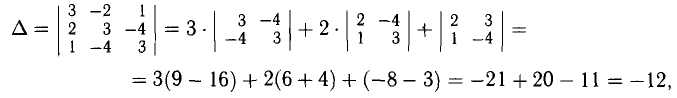
Следовательно, 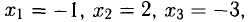
Пример:
Решение:
Вычисление следующих определителей основано на свойствах 2) и 5) из п. 6°. Имеем
Стрелка с числом обозначает умножение соответствующей строки на это число и прибавление результата к указанной стрелкой строке. Далее:
Пример:
Решение:
Имеем (предлагаем самостоятельно убедиться в этом):
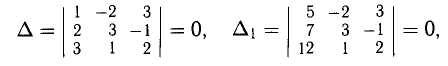
Система неопределенно совместна. Покажем, как обойтись формулами Крамера в этом случае.
Если первое уравнение прибавим ко второму, то получаем систему
Не прибегая к методу Жордана-Гаусса, перепишем систему так (это будет модифицированная система):
Следовательно, 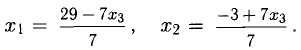
Общее решение имеет вид 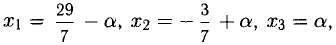
Пример:
Решение:
Теорема Крамера непосредственно к этой системе не применима, так как система не квадратная. Тем не менее систему можно решить относительно трех каких-либо неизвестных, если соответствующий определитель отличен от нуля. Перепишем систему в виде
Основной определитель
Вторая (модифицированная) система может быть решена по формулам Крамера, если принять в качестве свободных членов выражения, стоящие в правых частях уравнений (они содержат свободные неизвестные, что и оправдывает их название). Рекомендуем проверить равенства:
(перепишите общее решение в параметрической форме);
Метод обратной матрицы
1°. Матрицей размерности 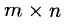
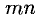
Можно обозначать 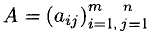
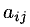
Две матрицы называются равными, если они имеют одинаковые размерности и элементы, стоящие на одинаковых местах (i,j), равны.
Матрица 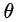
Если число строк m матрицы (6) равно числу столбцов n, то такая матрица называется квадратной.
Элементы квадратной матрицы 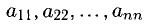
Квадратная матрица Е называется единичной, если все элементы ее главной диагонали равны 1, а все остальные — нулю:
Замена строк столбцами, а столбцов — строками (с сохранением их порядка) называется транспонированием матрицы.
2°. Для матриц определяются три действия: умножение матриц на число, сложение (вычитание) и умножение матриц.
1) Произведение матрицы А на число 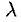
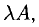
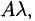
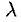
2) Суммой А + В (разностью А — В) матриц А и В одинаковой размерности называется матрица С, каждый элемент 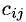
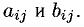
Например, (2 — 1 4) + (0 2 5) = (2 1 9);
3) Произведение АВ определяется не для произвольных матриц A и В. Оно имеет смысл только в том случае, когда число столбцов
А равно числу строк В. При этом 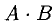
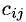
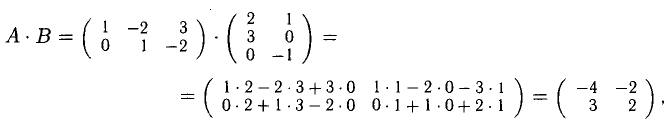
сравнивая 
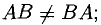
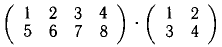
— это «редкий случай», когда
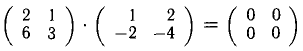
3°. Действия с матрицами обладают следующими свойствами:
2) АЕ = ЕА = А <А — квадратная матрица). Например,
если 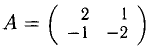
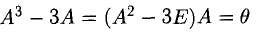
3)
Например, в этом можно убедиться на следующих парах матриц:
5°. Квадратная матрица А называется невырожденной, если соответствующий определитель (называемый определителем матрицы и обозначаемый det А) отличен от нуля; если det А = 0, то А называется вырожденной матрицей.
Матрица, обозначаемая 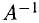
Теорема:
Если А — невырожденная квадратная матрица, то для нее существует обратная матрица, которая может быть определена по формуле
где 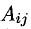
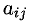
6°. Система из m линейных уравнений с n неизвестными может быть записана в матричной форме так (согласно определениям произведения матриц и равенства матриц):
Теорема:
Если (7) — квадратная система (т = п) и 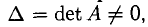
7°. Обратную матрицу можно найти методом элементарных преобразований Жордана-Гаусса, а вычисления производить в таблице Гауcса. Блоки таблицы Гаусса делятся на две равные части. В левую часть блока заносятся элементы квадратной невырожденной матрицы А, для которой надо найти обратную матрицу 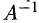
Примеры с решениями
Пример:
Решить систему
Решение:
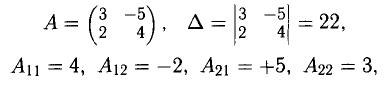
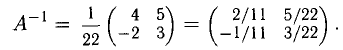
Получили 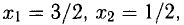
Пример:
Решение:
Следовательно, А — невырожденная матрица, поэтому она обладает обратной матрицей 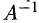
Вычислим 9 алгебраических дополнений:
Согласно теореме 1
Настоятельно рекомендуем проверить равенства
Таким образом, по теореме 5, имея в виду обозначения (8), получаем
Пример:
Найти 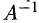
Решение:
В левую часть первого блока таблицы Гаусса заносим элементы матрицы А. В правую часть блока записываем единичную матрицу третьего порядка. Переход от одного блока к следующему осуществляем при помощи формул Жордана-Гаусса. Ведущие коэффициенты обведены. Рабочая таблица имеет следующий вид:
Ранг матрицы. Исследование систем
1°. Обратимся к матрице (6) . В ней фиксируем некоторые 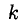
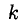
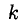
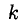
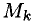
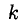
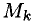
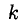
2°. Простейший способ определения ранга матрицы состоит в приведении ее к ступенчатому виду или к единичным столбцам при помощи последовательности элементарных преобразований, к которым относятся:
— умножение строки на произвольное число, отличное от нуля;
— прибавление к некоторой строке любой другой строки, умноженной на любое число;
— вычеркивание нулевой строки.
Элементарным преобразованиям матрицы соответствуют элементарные преобразования системы уравнений.
Теорема:
Элементарные преобразования матрицы не меняют ее ранг.
Между рангом матрицы А и рангом системы уравнений 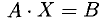
Теорема:
Ранг системы уравнений равен rank А.
4°. Иногда важно знать, совместна или нет система уравнений 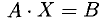
Если к матрице А присоединим столбец В свободных членов системы, то получаем расширенную матрицу
Теорема:
Теорема Кронекера-Капелли. Для совместности системы. уравнений 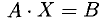
4°. Однородной называется система уравнений
Эта система всегда имеет нулевое решение 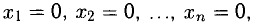
В связи с однородной системой возникает вопрос: при каких условиях она имеет нетривиальное (ненулевое) решение? Ответ выражается через соотношение m и n в терминах ранга матрицы А, составленной из коэффициентов системы при неизвестных.
Теорема:
Если 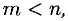
Теорема:
Система (9) имеет ненулевое решение, если
Свойства множества ненулевых решений однородной системы выражаются теоремой.
Теорема:
1) Если 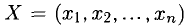
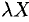
2) Если 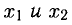
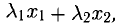
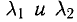
5°. Предположим, что однородную систему (9) можно разрешить относительно 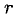
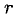
Неизвестные 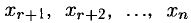
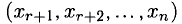
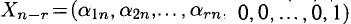
Множество этих решений называется фундаментальной системой решений (9).
Теорема:
О структуре общего решения однородной системы. Общее решение однородной системы представляет собой линейную комбинацию решений фундаментальной системы
где 
Рассмотрим теперь неоднородную систему
Система (9) называется однородной системой, соответствующей неоднородной системе (10).
Теорема:
О структуре общего решения неоднородной системы. Общее решение 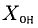
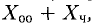
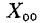
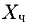
Примеры с решениями
Пример:
Определить ее ранг.
Решение:
Миноры более высоких порядков составлять нельзя. Ответ: rank А = 3.
Пример:
Найти ранг матрицы
Решение:
После вычитания первой строки из всех остальных (из последней — с множителем 2) получаем эквивалентную матрицу
Поскольку три строки промежуточной матрицы были пропорциональны, то из них можно получить две нулевые строки, которые мы отбросили.
Ясно, что rank А = 2, ибо
Пример:
Выяснить, разрешима ли система
Решение:
Напишем расширенную матрицу и получим в ней как можно больше единичных столбцов. Каждый раз ведущий коэффициент обведем кружком:
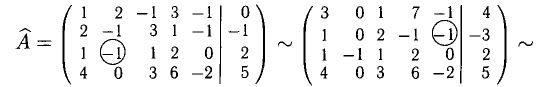
На языке (в терминах) уравнений последней строке соответствует уравнение 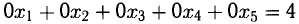
В расширенной матрице последняя строка ненулевая. Найдем в ней минор 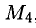
(разложили по последней строке). Итак 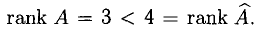
Пример:
Решение:
Решим сначала однородную систему
Вычтем из третьего уравнения сумму первых двух. Получим тривиальное уравнение, которое отбросим. Затем из второго уравнения вычтем первое. Получим равносильную систему
Свободным переменным 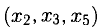
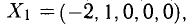
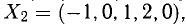
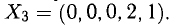
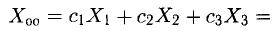
Для получения общего решения неоднородной системы нужно какое-то частное решение. Заметим, что 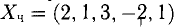
где 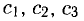
Отсюда при различных значениях постоянных 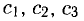
Системы линейных уравнений и их вычисление
Системой линейных алгебраических уравнений, содержащей m уравнений и п неизвестных, называется система вида
где числа 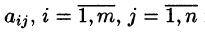
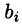
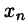
Такую систему удобно записывать в компактной матричной форме
Здесь А — матрица коэффициентов системы, называемая основной матрицей:

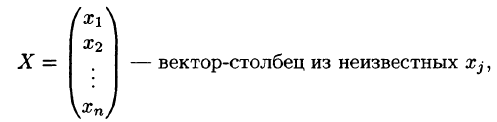
Произведение матриц 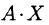
Расширенной матрицей системы называется матрица 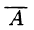
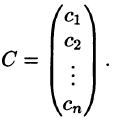
Решением системы называется п значений неизвестных 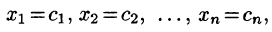
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда совместна, так как 
Решение систем линейных уравнений. Теорема Кронекера-Капелли
Пусть дана произвольная система m линейных уравнений с п неизвестными
Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кронекера-Капелли.
Теорема:
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Примем ее без доказательства. Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема:
Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема:
Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Правило решения произвольной системы линейных уравнений
- Найти ранги основной и расширенной матриц системы. Если
то система несовместна.
- Если
, система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные п — r неизвестных называют свободными и переносят в правые части уравнений.
- Найти выражения главных неизвестных через свободные. Получено общее решение системы.
- Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.
Пример:
Исследовать на совместность систему
Решение:
Таким образом, 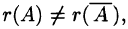
Пример:
Решение:
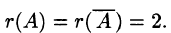
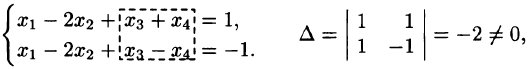
Следовательно, 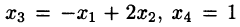
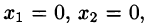
Решение невырожденных линейных систем. Формулы Крамера
Пусть дана система п линейных уравнений с п неизвестными
или в матричной форме
Основная матрица А такой системы квадратная. Определитель этой матрицы
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.
Найдем решение данной системы уравнений в случае 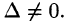
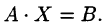
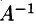
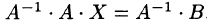
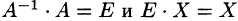
Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.
Матричное равенство (4.1) запишем в виде
Отсюда следует, что
Но 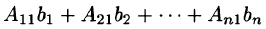
по элементам первого столбца. Определитель 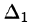

Аналогично: 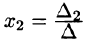
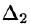

называются формулами Крамера.
Итак, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).
Пример:
Решение:
Значит,
Решение систем линейных уравнений методом Гаусса
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных. Пусть дана система уравнений
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
где 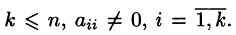
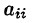
На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Опишем метод Гаусса подробнее. Прямой ход.
Будем считать, что элемент 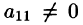
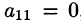
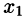
Преобразуем систему (4.3), исключив неизвестное 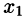
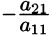
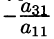
Здесь 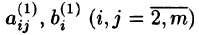
Аналогичным образом, считая главным элементом 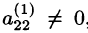
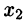
Если в процессе приведения системы (4.3) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида 0 = 0, их отбрасывают. Если же появится уравнение вида 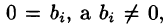
Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное 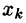
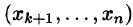
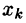
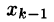
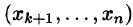
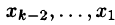
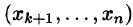
Замечанья: 1. Если ступенчатая система оказывается треугольной, т. е. 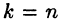
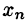
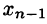
На практике удобнее работать не с системой (4.3), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент 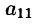
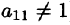
Пример:
Решить систему методом Гаусса:
Решение:
В результате элементарных преобразований над расширенной матрицей системы
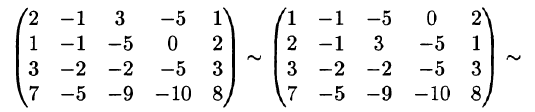
исходная система свелась к ступенчатой:
Поэтому общее решение системы: 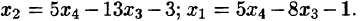
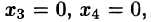
Пример:
Решить систему методом Гаусса:
Решение:
Произведем элементарные преобразования над строчками расширенной матрицы системы:
Полученная матрица соответствует системе
Осуществляя обратный ход, находим
Системы линейных однородных уравнений
Пусть дана система линейных однородных уравнений
Очевидно, что однородная система всегда совместна 
При каких условиях однородная система имеет и ненулевые решения?
Теорема:
Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг г ее основной матрицы был меньше числа п неизвестных, т. е. r
Теорема:
Для того, чтобы однородная система п линейных уравнений с п неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель 
Если система имеет ненулевые решения, то 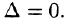
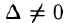
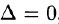
Решение:
Так как r 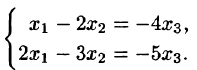
Положив 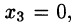
Положив 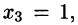
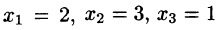
Теория к системам линейных алгебраических уравнений
Пусть дано n неизвестных 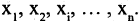
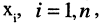
здесь 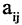
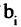
или в матричной форме 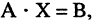
Матрица А называется основной (базовой) матрицей системы, X — Матрица-столбец неизвестных, В — матрица-столбец свободных членов. Если к основной матрице системы приписать столбец свободных членов, то получится расширенная матрица системы уравнений
Если все свободные члены равны нулю, то система называется однородной, в противном случае система неоднородна. Линейные системы, полученные одна из другой путем элементарных преобразований (перестановкой двух уравнений, умножением одного из них на число, не равное нулю, почленным сложением двух уравнения), называются эквивалентными (или равносильными). Все эквивалентные системы имеют одинаковые решения. Число линейно независимых уравнений в системе (2.34) называется рангом этой системы.
Система (2.34) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения. Линейная система (2.34) является совместной, если ранг расширенной матрицы системы был равен рангу ее основной матрицы, т. е.
Пример:
Определить совместимость системы:
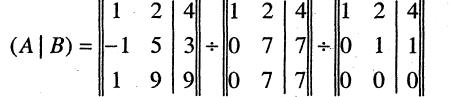
Составим расширенную матрицу системы и проведем с ней ряд элементарных преобразований, не меняющих ранг матрицы
Первую строку оставим без изменения, а во второй и третьей строках с помощью элементарных преобразований (от второй строки отнимем первую, а к третьей прибавим первую строку) в первом столбце получим нули, т. е:
Вычитая из третьей строки вторую, получим
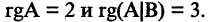
Для совместной системы линейных уравнений возможны следующие случаи.
1.Если 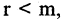
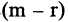
2.Если 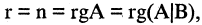
3.Если 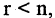
Пример. Исследовать систему уравнений
Здесь 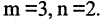
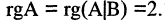
Решение этой системы:
Пример:
Построим расширенную матрицу
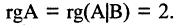
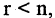
и положив 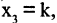
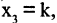
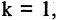
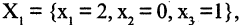
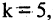
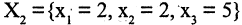
Если число уравнений n равно числу неизвестных n, то система имеет вид
Если матрица А невырожденная 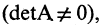
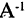
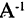
Решение квадратной системы алгебраических уравнений в матричной форме сводится к построению обратной к А матрицы и последующему умножению ее справа на матрицу свободных членов:
Пример:
Решить систему алгебраических уравнений
Решение:
Вычислим определитель матрицы системы
Найдем алгебраические дополнения элементов матрицы А
Присоединенная матрица и обратная матрица соответственно равны
По формуле (2.37) получим решение системы
Всякая однородная система
совместна, так как всегда имеет хотя бы нулевое решение: 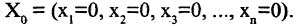
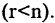
Пример:
Исследовать и найти решение системы
Решение:
В данном примере 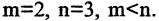
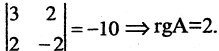
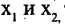
бираем 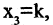
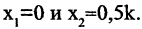
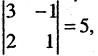
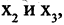
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Системы линейных уравнений
Обозначим через $ \mathbb A_<> $ любое из множеств $ \mathbb Q_<>, \mathbb R_<> $ или $ \mathbb C_<> $.
Примеры систем уравнений над $ \mathbb R $.
Относительно числа $ m_<> $ уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных $ n_<> $. Если $ m_<>>n $ то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных $ x_1=\alpha_<1>,\dots, x_n = \alpha_n $, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.
Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:
1. система совместна и имеет единственное решение;
2. cистема совместна и имеет бесконечное множество решений;
3. cистема несовместна.
При этом все решения будут находиться в том же множестве $ \mathbb A_<> $, что и коэффициенты системы.
Матричная форма записи
Для системы линейных уравнений относительно переменных $ x_1,x_2,\dots,x_n $ $$ \left\< \begin
Исключение переменных (метод Гаусса)
метода достаточно проста.
Пример. Решить систему уравнений $$ \left\< \begin
Решение. Выразим из первого уравнения $ x_ <1>$ $$ x_1=\frac<3> <2>x_2+\frac<1> <2>x_3 + \frac<3> <2>$$ и подставим в оставшиеся уравнения $$ 4 \left(\frac<3> <2>x_2+\frac<1> <2>x_3 + \frac<3><2>\right) -3\,x_2-5\,x_3=6 \ <\color
Ответ. $ x_<1>=1/4, x_2=-5/8, x_3=-5/8 $.
Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.
Исключение переменных
Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:
1. перестановка двух уравнений;
2. умножение обеих частей уравнения на любое отличное от нуля число;
3. прибавление к одному уравнению любого другого, умноженного на произвольное число: пара уравнений $$ \begin
Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.
Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.
Предположим, что первое уравнение системы содержит явно неизвестную $ x_ <1>$, т.е. $ a_<11>^<> \ne 0 $. Исключим эту неизвестную из всех оставшихся уравнений. С этой целью вычтем из второго уравнения первое, домноженное на $ a_<21>/a_<11>^<> $. Получим $$\left(a_<22>— \frac
Понятно, что процесс исключения может быть продолжен и далее. Теперь посмотрим, где он может прерваться. Может так случиться, что очередная, $ \ell_<> $-я подсистема имеет коэффициент $ a_<\ell \ell>^ <[\ell-1]>$ равным нулю, что не позволит алгоритму идти дальше — т.е. исключить переменную $ x_<\ell>^<> $ из оставшихся уравнений (в принципе, такое могло случиться уже на первом шаге, если бы коэффициент $ a_<11>^<> $ был бы равен нулю). Возможные варианты дальнейших действий:
1. если хотя бы один коэффициент при $ x_<\ell>^<> $ в одном из оставшихся уравнений отличен от нуля: $ a_
2. если при всех $ j\ge \ell^<> $ коэффициенты $ a_
Поскольку число переменных конечно, то алгоритм исключения должен завершиться за конечное число шагов. Чем он может завершиться? Окончательная система должна иметь вид: $$ \left\< \begin
Предположение . Мы будем считать, что каждое из первых $ <\mathfrak r>_<> $ уравнений системы содержит в своей левой части хотя бы одну переменную с ненулевым коэффициентом.
Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.
Исторический комментарий о Гауссе ☞ ЗДЕСЬ.
Установление множества решений
Теорема. Если хотя бы одно из чисел $ b_<<\mathfrak r>+1>^<[<\mathfrak r>-1]>,\dots , b_
Для простоты мы будем иллюстрировать наши рассуждения на системах л.у. над $ \mathbb R_<> $, в этом же множестве искать решения. Каждое из преобразований метода Гаусса будем обозначать $ \to_<> $.
Пример. Решить систему л.у.
$$ \left\< \begin
Решение. $$ \ \to \ \left\< \begin
Ответ. Система несовместна.
Пусть теперь $ b_<<\mathfrak r>+1>^<[<\mathfrak r>-1]>=0,<>\dots, b_
Теорема. Если прямой ход метода Гаусса заканчивается треугольной системой, т.е. $ \mathfrak r = n_<> $ и $ b_<<\mathfrak r>+1>^<[<\mathfrak r>-1]>=0,<>\dots, b_
Пример. Решить систему л.у.
$$ \left\< \begin
Ответ. $ x_1=1,\, x_<2>=2,\, x_3=-2 $ .
Исследуем теперь случай $ <\mathfrak r>1) : 
Теорема. Если прямой ход метода Гаусса заканчивается трапециевидной системой, т.е. $ \mathfrak r 2) матрицы $ A_<> $ (третьего порядка). Понятие определителя распространяется и на квадратные матрицы бóльших порядков; образно говоря, определитель — это функция элементов матрицы, отвечающая за единственность решения системы уравнений.
Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.
Формулы Крамера
Рассмотрим систему линейных уравнений с квадратной матрицей $ A_<> $, т.е. такую, у которой число уравнений совпадает с числом неизвестных.
Теорема. Cистема
$$ \left\<\begin
Доказательство ☞ ЗДЕСЬ
Пример. Решить систему уравнений
$$ \left\<\begin
Решение. $$ x_1=\frac<\left|\begin
Решение системы линейных уравнений с квадратной матрицей $ A_<> $ является непрерывной функцией коэффициентов этой системы при условии, что $ \det A_<> \ne 0 $.
Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.
Еще один способ решения системы основан на построении обратной матрицы: $$ AX= <\mathcal B>\quad \Rightarrow \quad X=A^<-1> <\mathcal B>\ . $$ Этот способ малоэффективен при фиксированных числовых $ A_<> $ и $ <\mathcal B>_<> $.
Найти достаточное условие существования общего решения систем уравнений:
$$ A_1 X = <\mathcal B>_1 \quad u \quad A_2 Y = <\mathcal B>_2 \ , $$ при квадратных матрицах $ A_1 $ и $ A_2 $ одинакового порядка.
Теорема Кронекера-Капелли
Матрица, получающаяся конкатенацией матрицы $ A_<> $ и столбца правых частей $ <\mathcal B>_<> $ $$ [ A| <\mathcal B>] = \left( \begin
Теорема [Кронекер, Капелли]. Система $ AX= <\mathcal B>$ совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:
$$ \operatorname
Доказательство необходимости. Пусть существует решение $ x_1=\alpha_1,\dots,x_n=\alpha_n $ системы, тогда $$\alpha_1 A_<[1]>+\dots+\alpha_n A_<[n]>= <\mathcal B>\ ,$$ т.е. столбец $ <\mathcal B>$ линейно выражается через столбцы $ A_<[1]>,\dots,A_ <[n]>$. Но тогда $$ \operatorname
Доказательство достаточности проводится в следующем пункте. ♦
Пример. Исследовать совместность системы уравнений
Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы $ \det A_<> $. Если он отличен от нуля — система совместна. $$\det A = \left| \begin
Осталось исследовать критические случаи: $ <\color
При $ <\color
Ответ. Система несовместна при $ <\color
Система однородных уравнений
$$ \left\< \begin
Пример. Найти условие, при котором три точки плоскости с координатами $ (x_1,y_1), (x_2,y_2) $ и $ (x_3,y_<3>) $ лежат на одной прямой.
Решение. Будем искать уравнение прямой в виде $ ax+by+c=0 $ при неопределенных коэффициентах $ a,b,c_<> $. Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений: $$ \left\< \begin
Доказать, что для совместности системы
$$ \left\< \begin
An elementary treatise on determinants
в следующей формулировке.
Теорема. Для того чтобы система $ n_<> $ неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.
Додсон — один из самых знаменитых математиков мира. Назовите его псевдоним.
Ответ ☞ ЗДЕСЬ
Общее решение
Пусть выполнено условие теоремы Кронекера-Капелли: $ \operatorname
Пусть теперь $ \mathfrak
Пример. Исследовать совместность и найти общее решение системы уравнений:
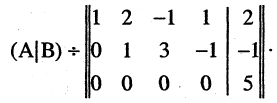
Решение проведем двумя способами, соответствующими двум способам вычисления ранга матрицы. Вычисляем сначала ранг матрицы $ A $ по методу окаймляющих миноров: $$ |2| \ne 0,\quad \left| \begin
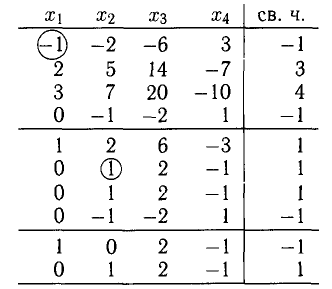
Ненулевой минор третьего порядка (базисный минор) находится в первой, второй и четвертых строках, что означает линейную независимость соответствующих уравнений. Третье уравнение линейно зависит от остальных, и может быть отброшено. Далее, указанный базисный минор образован коэффициентами при $ x_1,x_3 $ и $ x_4 $. Следовательно оставшиеся уравнения могут быть разрешены относительно этих переменных, т.е. они — зависимые, а $ x_2 $ и $ x_5 $ — основные. Использование формулы дает общее решение $$ \begin
Ответ. Общее решение системы: $ x_1=1/2 (x_2+x_5-1),\ x_3=3-4\,x_5,\ x_4=0 $.
Проанализируем теперь полученные общие формулы для общего решения. В этих формулах $ \beta_j $ представляет решение системы, получаемое при $ x_<\mathfrak
Вывод. Формула общего решения системы $ A X=\mathcal B $: $$ x_j=\beta_j + \gamma_
Теорема. Общее решение системы уравнений $ A X=\mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=\mathbb O $.
Доказательство тривиально если система $ A X=\mathcal B $ имеет единственное решение. Если же решений бесконечно много, то выбрав какое-то одно частное $ X=X_1 $ мы получаем, что любое другое частное решение $ X=X_2 $ должно быть связано с первым соотношением $$ A(X_2-X_1)=\mathbb O , $$ т.е. разность частных решений неоднородной системы обязательно является решением однородной системы уравнений $ AX=\mathbb O $. ♦
Теперь посмотрим как можно описать общее решение однородной системы.
Система однородных уравнений
Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю: $$ \left\< \begin
Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру, если матрица $ A_<> $ системы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет. Теорема Кронекера-Капелли утверждает, что условие $ \det (A_<>) = 0 $ является и достаточным для существования нетривиального решения.
Теорема 1. Для того, чтобы система однородных уравнений с квадратной матрицей $ A_<> $ имела нетривиальное решение необходимо и достаточно, чтобы $ \det (A_<>) = 0 $.
Для произвольной (не обязательно квадратной) матрицы $ A_<> $ имеет место следующий общий результат.
Теорема 2. Если $ \operatorname
Теорема 3. Множество решений системы однородных уравнений образует линейное подпространство пространства $ \mathbb A^
Пусть матрица системы $ AX=\mathbb O $ квадратная и
$$ \operatorname
Теперь обсудим способы нахождения ФСР.
1. Первый из них получается из общего метода решения системы линейных уравнений, рассмотренного в предыдущем пункте. Так же, как и в том пункте, сделаем упрощающее обозначения предположение, что зависимыми переменными являются первые $ x_<1>,\dots,x_ <\mathfrak r>$, т.е. общее решение задается формулами $$ x_j=\gamma_
Оформим этот способ построения ФСР в теорему:
Теорема 4. Если система уравнений $ AX=\mathbb O $ имеет структуру матрицы $ A_<> $ вида:
$$ A = \left[ E_ <\mathfrak r>\mid P_ <\mathfrak r \times (n-\mathfrak r)>\right] \ , $$ то ее ФСР состоит из столбцов матрицы $$ \left[ \begin
Пример. Найти ФСР для системы уравнений
Решение. Приводим систему к трапециевидному виду: $$ \left\< \begin
2. Этот способ напоминает вычисление обратной матрицы методом приписывания единичной матрицы. Транспонируем матрицу $ A_<> $ системы и припишем к ней справа единичную матрицу порядка $ n_<> $: $$ \left[ A^ <\top>| E_n \right] = \left(\begin
Пример. Найти ФСР для системы уравнений
$$ \left\< \begin
$$ \left(\begin
3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.
Теорема. Пусть матрица системы $ AX=\mathbb O $ квадратная и $ \operatorname
Пример. Найти ФСР для системы уравнений
Решение. Здесь $$ A= \left( \begin
Блок-схемы зависимости множества решений системы уравнений $ AX= \mathcal B $ от комбинации чисел $ n, \mathfrak r $ ☞ ЗДЕСЬ.
Геометрическая интерпретация
Геометрический смысл введенных определений поясним на примере $ \mathbb R^ <3>$. Уравнение $$ a_1x_1+a_2x_2+a_3x_3=b $$ — при фиксированных вещественных коэффициентах $ a_1,a_2,a_3 $ (хотя бы один из них считаем отличным от нуля) и $ b_<> $ — задает плоскость. Если, к примеру, $ a_1\ne 0 $, то из уравнения получаем выражение для $ x_ <1>$ как функции $ x_2,x_3 $: $$ x_1=\frac
Теорема. Общее решение системы уравнений $ A X=\mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=\mathbb O $.

Теперь рассмотрим систему из двух уравнений: $$ \left\<\begin
Мы рассмотрели пока только случай пересекающихся плоскостей в пространстве. Его можно считать общим, т.е. случаем «как правило»: две случайным образом выбранные плоскости в $ \mathbb R^ <3>$ пересекаться будут. Исследуем теперь исключительный случай — параллельности плоскостей. Исключительность этого случая может быть проверена и аналитикой. Для несовместности системы из двух уравнений необходимо, чтобы ранг ее матрицы $$ \left( \begin
Перейдем теперь к системе из трех уравнений: $$ \left\< \begin
Теорема Кронекера-Капелли в этом случае не нужна — нет, она остается справедливой! — но проверка условия на ранги матриц тривиальна: они оба равны $ 3_<> $. Если же указанный определитель обращается в нуль, то этот факт эквивалентен тому, что три строки определителя линейно зависимы. Например, возможно, что строка $ (a_<31>,a_<32>, a_<33>) $ может быть представлена в виде линейной комбинации первых двух строк. Вспомним геометрический смысл этих строк: они задают координаты векторов, перпендикулярных соответствующим плоскостям. Если система уравнений $$ \left\<\begin
Статья не закончена!
Ортогональность
Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.
Задача решения системы линейных уравнений $$ \left\< \begin
С другой стороны, к той же задаче решения системы уравнений, в предыдущем ПУНКТЕ мы подошли с другой стороны. Первое из уравнений системы $$ 3\,x_1+4\,x_2-x_3=2 $$ можно интерпретировать так: скалярное произведение векторов $ \vec<<\mathbf OA>^<[1]>> $ и $ \vec<<\mathbf OX>> $ равно фиксированному числу $ 2_<> $. Здесь вектора рассматриваются в пространстве строк $ \mathbb R_<>^ <3>$; считается, что каждый вектор имеет начало в начале координат $ \mathbf O=[0,0,0] $, а конец — в точке с координатами $ [3,4,-1] $ или, соответственно, $ [x_1,x_2,x_3] $. Если скалярное произведение векторов обозначать скобками $ \langle <> \mbox < >\rangle $, то систему уравнений можно переписать в виде $$ \langle \vec<<\mathbf OA>^<[1]>> ,\ \vec<<\mathbf OX>> \rangle=2,\ \langle \vec<<\mathbf OA>^<[2]>> ,\ \vec<<\mathbf OX>> \rangle=1 \quad npu \quad A^ <[1]>= [3,4,-1], A^<[2]>=[1,-2,3] $$ — строках матрицы $ A_<> $. И задачу решения такой системы понимать в смысле: найти координаты всех векторов-строк $ [x_1,x_2,x_3] $ которые обеспечат нам заданные значения скалярных произведений с двумя фиксированными векторами.
Геометрическая интерпретация еще более упрощается если рассмотреть случай однородной системы уравнений. Так, решить систему уравнений $$ \left\< \begin
Все эти геометрические соображения обобщаются в произвольное пространство $ \mathbb R_<>^
В терминах скалярного произведения, задачу решения системы линейных уравнений можно переформулировать как поиск строки $ X=[x_1,x_2,\dots,x_n] $, ортогональной всем строкам матрицы $ A_<> $: $$ \langle A^<[1]>,X \rangle=0, \langle A^<[2]>,X \rangle=0,\dots, \langle A^<[m]>,X \rangle=0 \ . $$ Множество таких строк образует линейное подпространство пространства $ \mathbb R_<>^
Теорема. $ \operatorname
Матрицы: метод Гаусса. Вычисление матрицы методом Гаусса: примеры
Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Основные понятия
Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.

Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.
Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
Ступенчатый вид матрицы
Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l Понравилась статья? Поделись с друзьями:
http://vmath.ru/vf5/algebra2/linearsystems
http://1ku.ru/obrazovanie/56526-matricy-metod-gaussa-vychislenie-matricy-metodom-gaussa-primery/
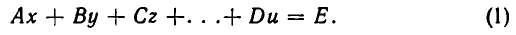
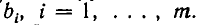
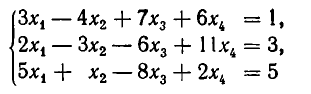
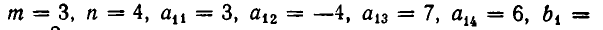
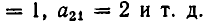

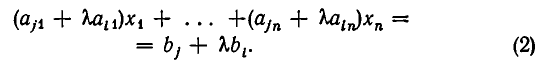
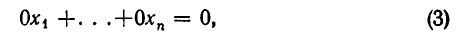
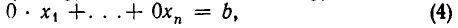
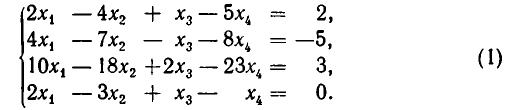
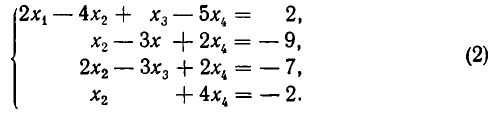
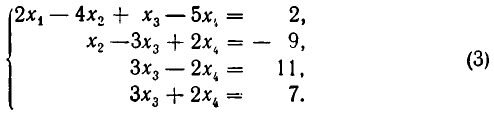
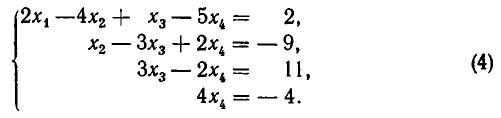
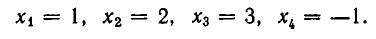
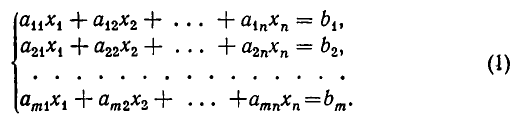
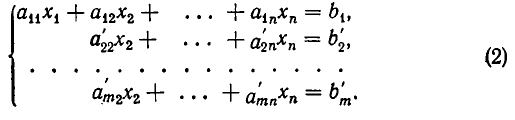
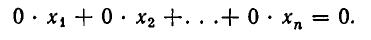

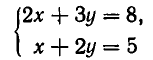
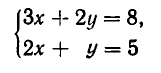
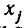

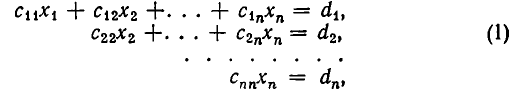
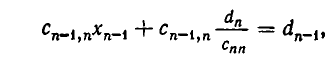
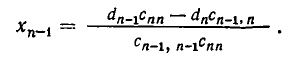
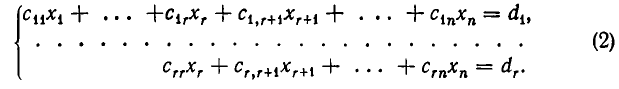
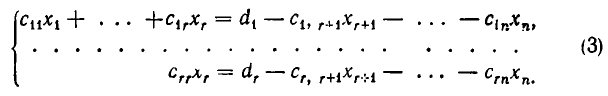
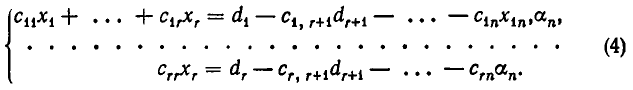
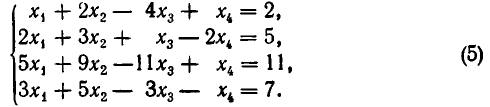
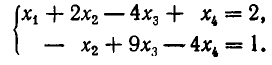
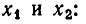
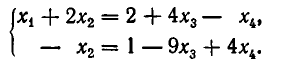
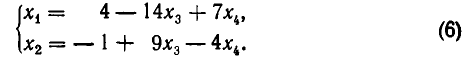
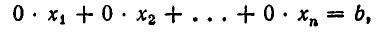
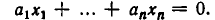
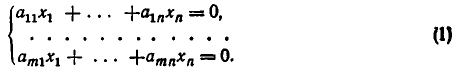
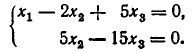
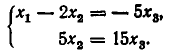
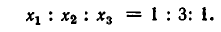
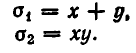
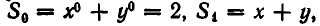
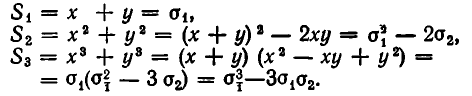
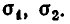

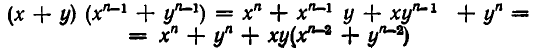
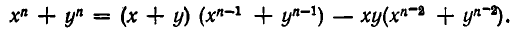
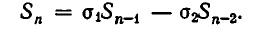
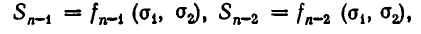
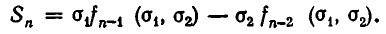
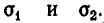
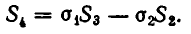
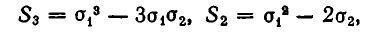
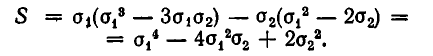
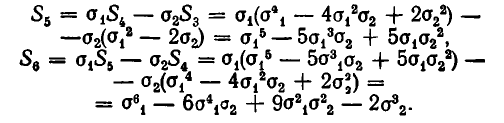
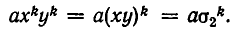
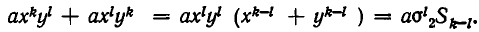
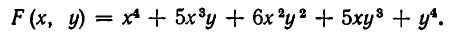
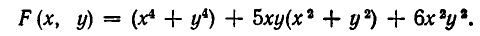
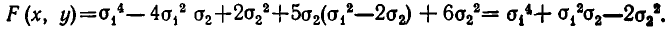



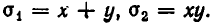
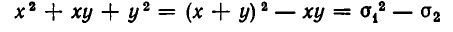
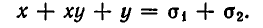
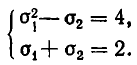
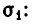
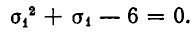
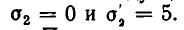
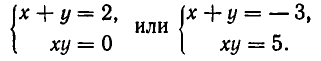
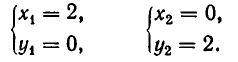
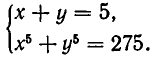
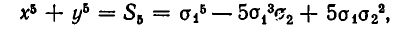
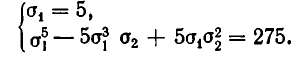
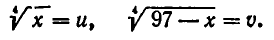
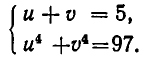
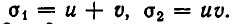
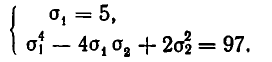
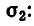
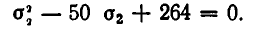
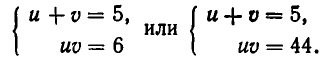
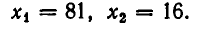
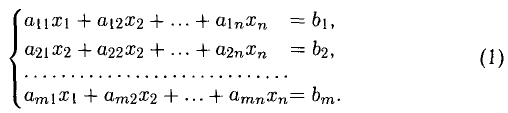
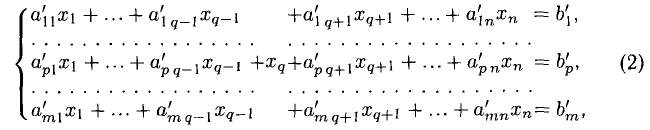
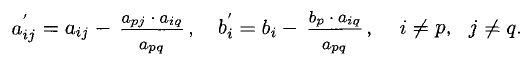
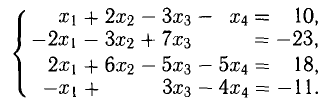

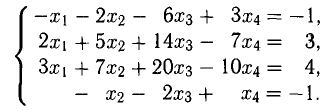
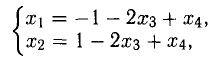
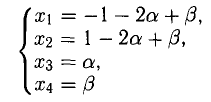
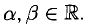
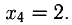
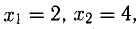
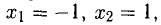
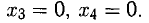
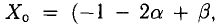
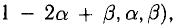
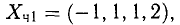
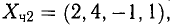
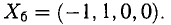
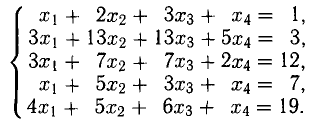
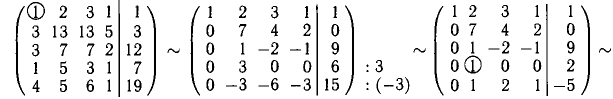
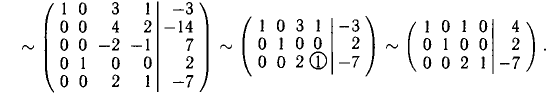
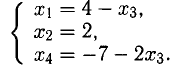
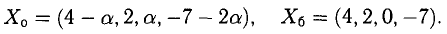
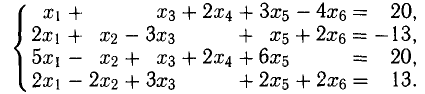
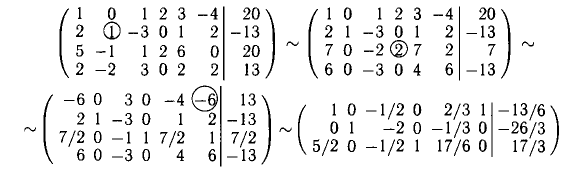
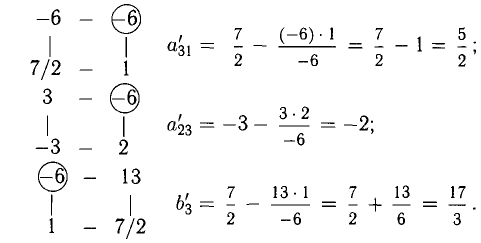
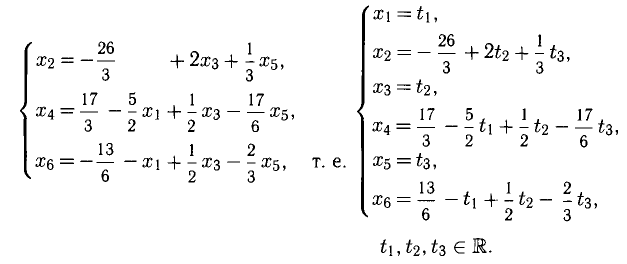
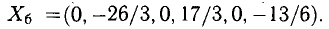
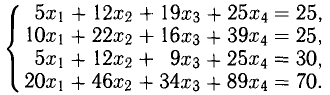

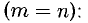
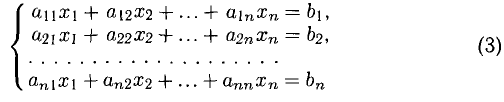
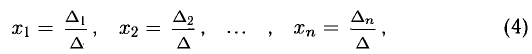
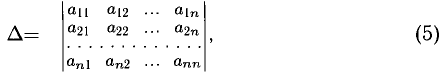
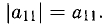
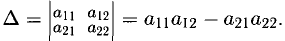
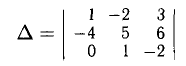
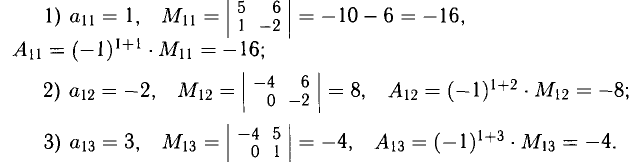
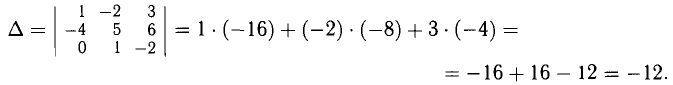
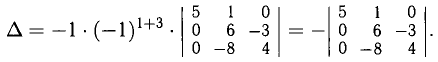
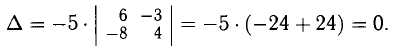
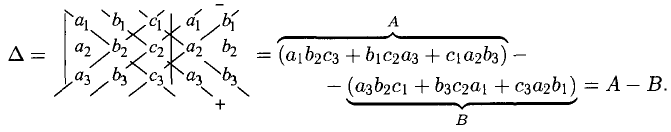
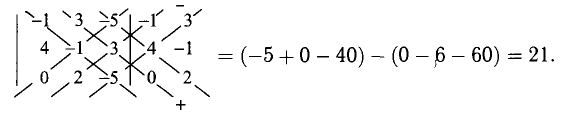
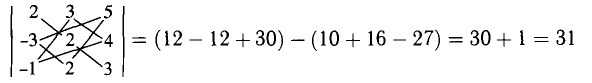
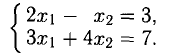
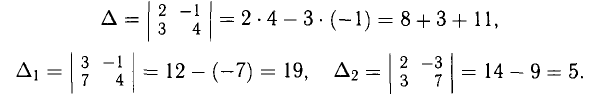
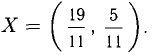
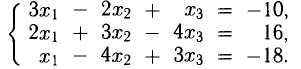
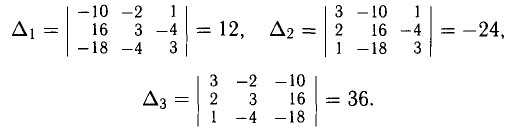
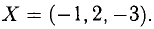
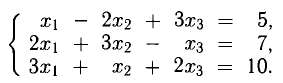
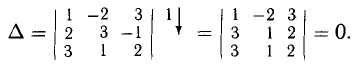
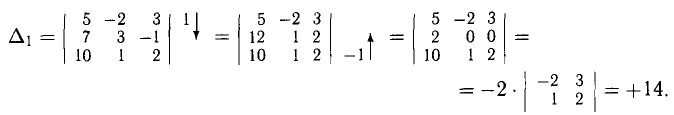
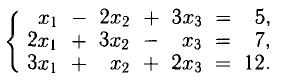
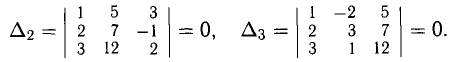

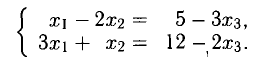
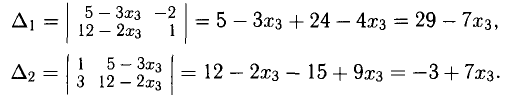
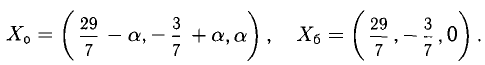
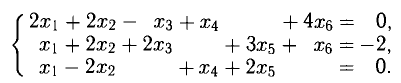
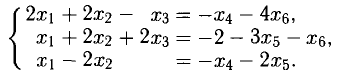
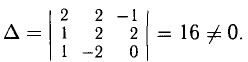
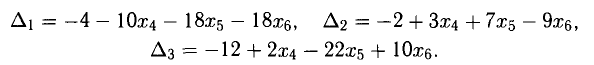
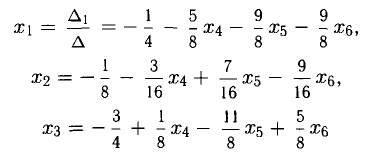
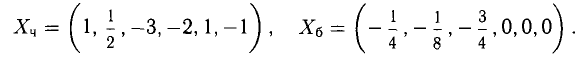
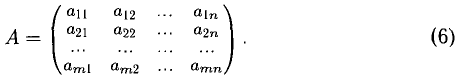


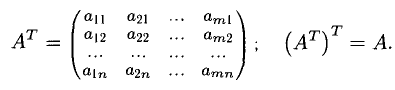
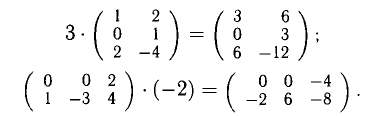
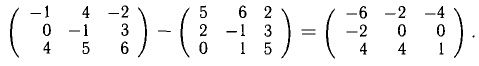
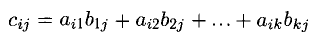
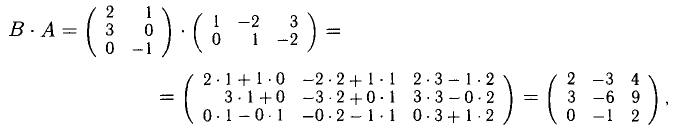
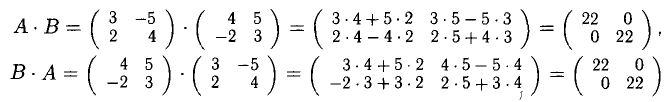
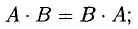
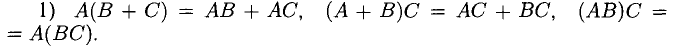
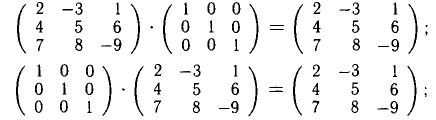
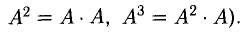
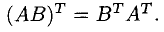
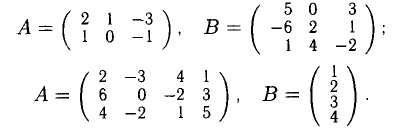
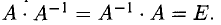
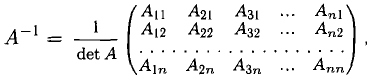

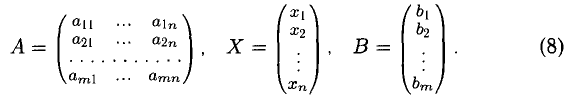
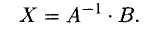
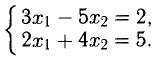
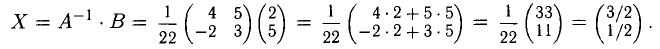
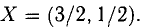
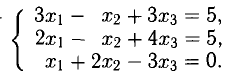
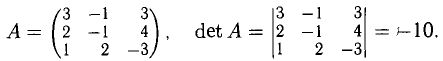
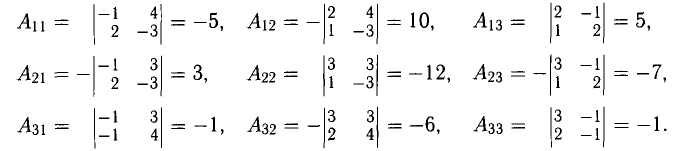
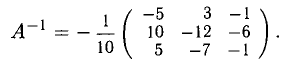
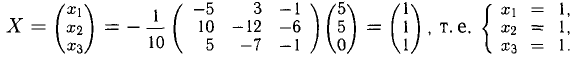
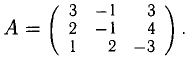

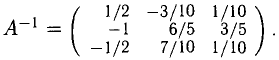
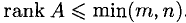
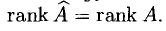
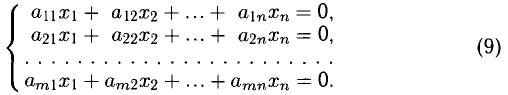
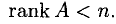
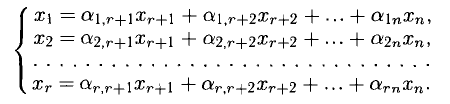
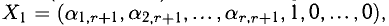
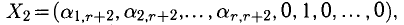
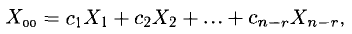
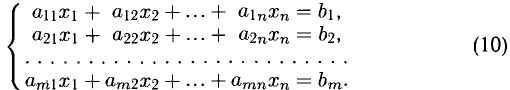

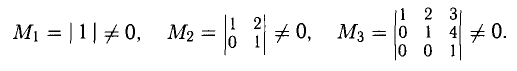
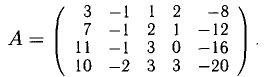
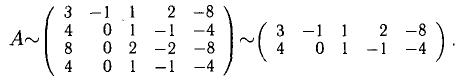
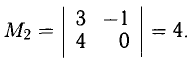
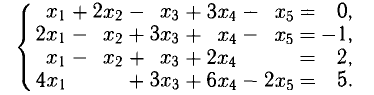
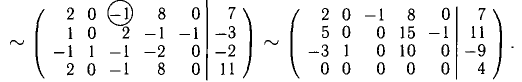
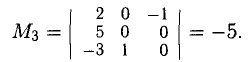
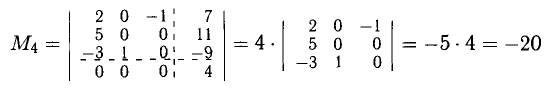
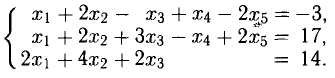
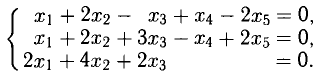

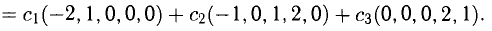
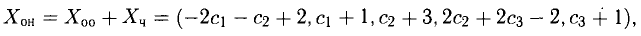
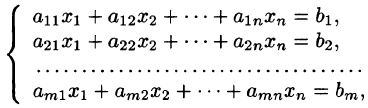
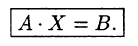
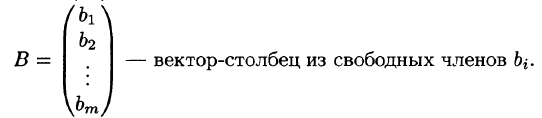

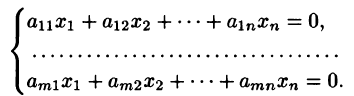
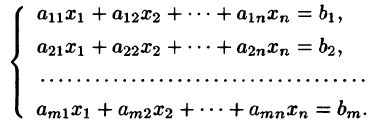
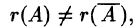 то система несовместна.
то система несовместна.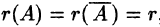 , система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные п — r неизвестных называют свободными и переносят в правые части уравнений.
, система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные п — r неизвестных называют свободными и переносят в правые части уравнений.