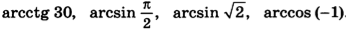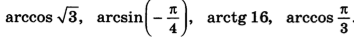Алгебра 10 Мерзляк КР-6
Контрольная работа № 6 по алгебре для 10 класса «Тригонометрические уравнения и неравенства» УМК Мерзляк Базовый уровень (два варианта). Цитаты из пособия «Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Базовый уровень» (авт. А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович, М.С.Якир, изд-во «Вентана-Граф») использованы на сайте в незначительных объемах, исключительно в учебных целях (пп. 1 п. 1 ст. 1274 ГК РФ). Алгебра 10 Мерзляк КР-6.
Алгебра 10 класс (Мерзляк)
Контрольная работа № 6.
Тригонометрические уравнения и неравенства.
КР-6. Вариант 1.
1. Решите уравнение: 1) sin (8x – π/3) = 0; 2) cos ( x /6 + π/4) = √2/2; 3) tg 2 4 x + tg 4 x = 0.
2. Решите неравенство: 1) cos ( x /7) ≤ 1/2; 2) ctg (7x + 2π/3) > –√3/3
3. Решите уравнение : 1) 4cos 2 x + 4sin x – 1 = 0; 2) 3sin 2 3x – 2,5sin 6x + 1 = 0; 3) sin 9 х + sin 8x + sin 7x = 0.
4. Вычислите : 1) sin (arcsin 5 / 8 ); 2) cos (arcsin 5 / 13 ).
5. Решите уравнение sin 6x + √3 cos 6x = –2 cos 8x.
КР-6. Вариант 2.
Вы смотрели: Контрольная работа № 6 по алгебре «Тригонометрические уравнения и неравенства» для 10 класса УМК Мерзляк Базовый уровень. Цитаты из пособия «Дидактические материалы. Алгебра и начала математического анализа. 10 класс. Базовый уровень». Алгебра 10 Мерзляк КР-6.
Алгебра 10 Мерзляк КР-6: 4 комментария
какой есть способ решения 5 номера?
Решение добавлено в статью (необходимо открыть спойлер).
скиньте ответы на все номера
Добавить комментарий Отменить ответ
Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.
Предметы
Новые работы
Найти контрольную:
Авторы работ и УМК
Предметы
Важные страницы
Соглашение о конфиденциальности
(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru
Популярное
Предупреждение
Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Простейшие тригонометрические уравнения (задание 5) и неравенства
\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad \mathrm
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\) ).
Рассмотрим несколько примеров:
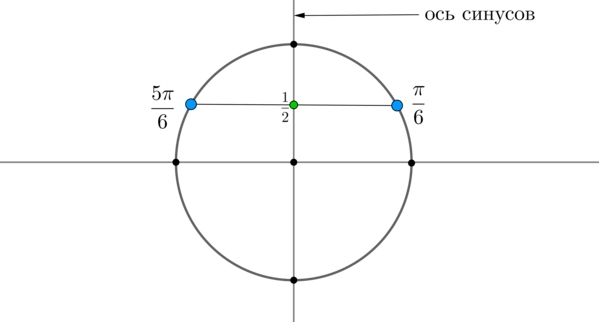
Пример 1. Решить уравнение \(\sin x=\dfrac12\) .
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\) , где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).
Таким образом, решением являются \(x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb
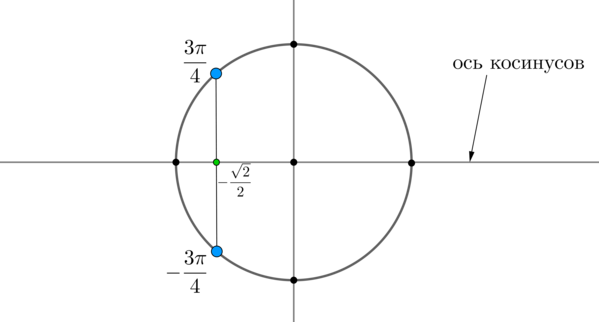
Пример 2. Решить уравнение \(\cos x=-\dfrac<\sqrt2><2>\) .
Найдем на оси косинусов точку \(-\dfrac<\sqrt2><2>\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac<\sqrt2><2>\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<3\pi>4\) и \(-\dfrac<3\pi>4\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число.
Таким образом, решением являются \(x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb
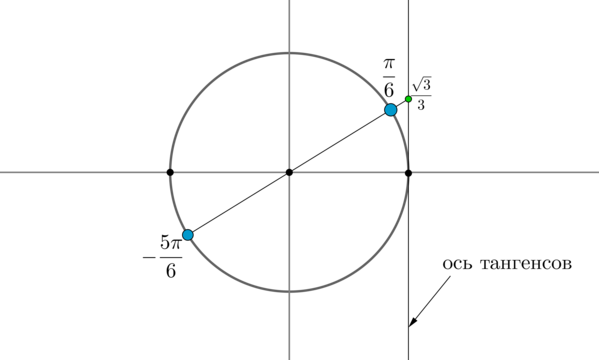
Пример 3. Решить уравнение \(\mathrm
Найдем на оси тангенсов точку \(\dfrac<\sqrt3>3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac<\sqrt3>3\) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .
Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb
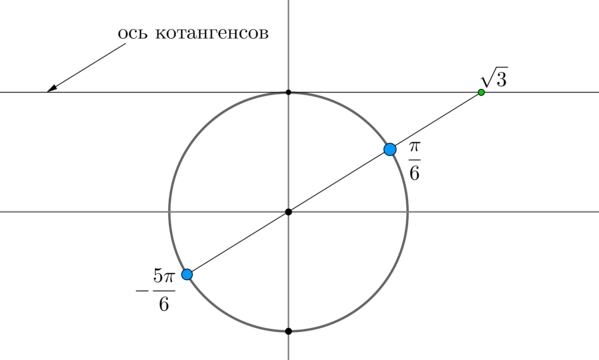
Пример 4. Решить уравнение \(\mathrm
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .
Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb
\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin
\(\blacktriangleright\) Любые уравнения вида \(\mathrm
Пример 5. Решить уравнение \(\sin<(\pi x+\dfrac<\pi>3)>=1\) .
Сделав замену \(t=\pi x+\dfrac<\pi>3\) , мы сведем уравнение к виду \(\sin t=1\) . Решением данного уравнения являются \(t=\dfrac<\pi>2+2\pi n, n\in\mathbb
Теперь сделаем обратную замену и получим: \(\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n\) , откуда \(x=\dfrac16+2n,\ n\in\mathbb
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb
Рассмотрим данную ситуацию на примере:
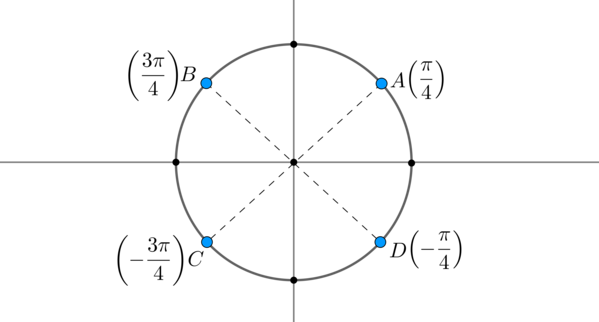
Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb
Заметим, что длины дуг \(\buildrel\smile\over
где \(\lor\) — один из знаков \(\leq,\ ,\ \geq\) .
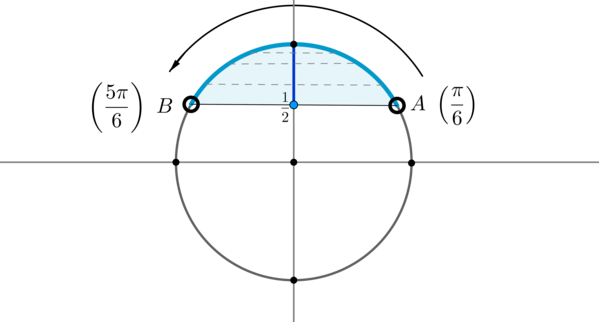
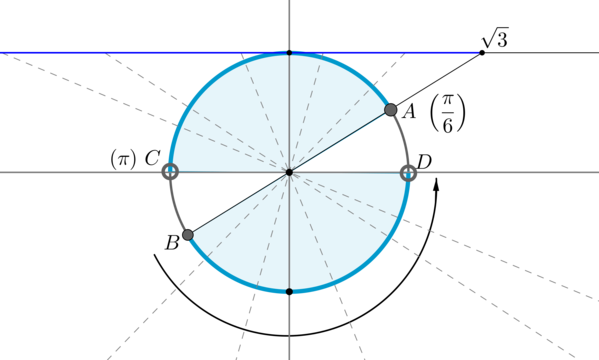
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\) .
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, синус которых больше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .
Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>6\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>6\) , но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>6\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb
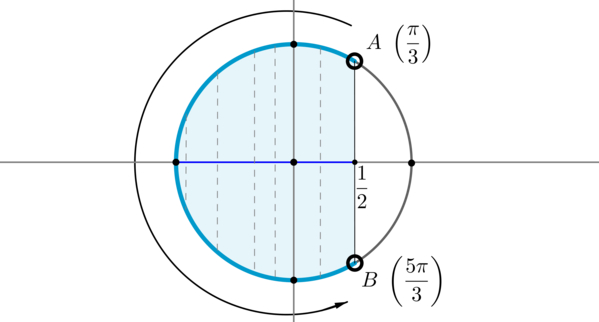
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, косинус которых меньше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .
Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>3\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>3\) , но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>3\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm
Для начала отметим на окружности корни уравнения \(\mathrm
Рассмотрим одну из дуг, например, \(\buildrel\smile\over
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm
Для начала отметим на окружности корни уравнения \(\mathrm
Рассмотрим одну из дуг, например, \(\buildrel\smile\over
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
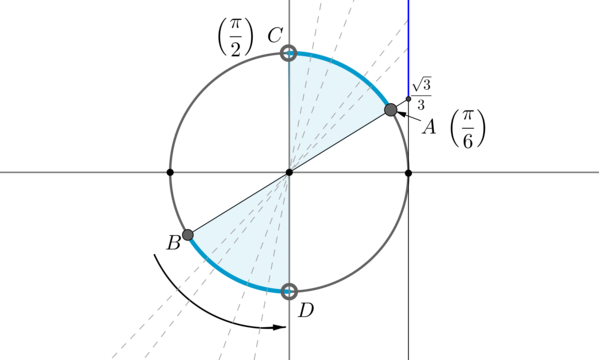
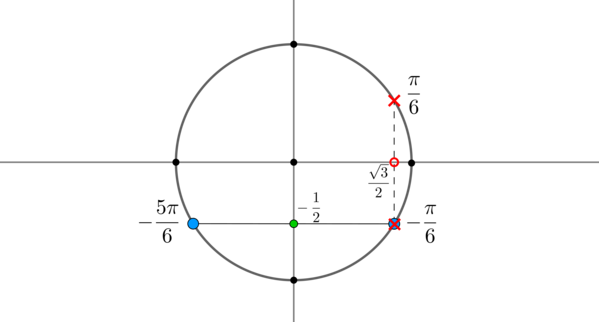
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\) , если \(\cos x\ne \dfrac<\sqrt3>2\) .
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac<\pi>6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin
Пример 12. Решить систему \(\begin
Решением уравнения являются \(x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb
\(\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0\) , следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac<\sqrt2>2\) , принадлежащие отрезку \([0;\pi]\) .
Решением уравнения являются \(x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb
\(0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\) . Таким образом, единственное целое значение \(n\) , удовлетворяющее этому неравенству, это \(n=0\) . При \(n=0\) \(x_1=\dfrac<\pi>4\) — входит в отрезок \([0;\pi]\) .
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac<3\pi>4\) .
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\) .
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\) , то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\) . Т.к. \(НОД(3,5)=1\) , то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\) :
Число \(\dfrac<2-2y>3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\) : \(0\) , \(1\) или \(2\) .
Если \(y\) при делении на \(3\) имеет остаток \(0\) , то оно записывается как \(y=3p+0\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]
Если \(y\) при делении на \(3\) имеет остаток \(1\) , то оно записывается как \(y=3p+1\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\) , а \(x=\dfrac<2-2y>3-y=-5p-1\) .
Ответ: \((-5p-1; 3p+1), p\in\mathbb
Перейдем к примеру:
Пример 14. Решить систему \[\begin
Решим первое уравнение системы:
\[\left[ \begin
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\) , при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\) :
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\) , то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\) , при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\) :
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac<3m+1>2=m+\frac
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\) .
Если \(m=2p+0\) , то \(\frac
Если \(m=2p+1\) , то \(\frac
Значит, \(m=2p+1\) , тогда \(k=3p+2\) , \(p\in\mathbb
Подставим либо \(m\) , либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb
Тест по теме: «Тригонометрические уравнения и неравенства» 10 класс
Данная разработка содержит тест по алгебре для 10 класса. Тематическое тестирование в 18 вариантах, с заданиями части В и частиС.
Просмотр содержимого документа
«Тест по теме: «Тригонометрические уравнения и неравенства» 10 класс»
Тест «Тригонометрические уравнения и неравенства»
В1. Вычислите: arcsin 1/2 — π/9
В2. Вычислите: arctg 1/√3+ π/6
В3. Вычислите: arcctg √3
В4. Решите уравнения: А)sin( x + π/4) = -1 б) cos 12x = -1
В5. Найдите выражения, не имеющие смысла:
С 1. Решите уравнение cos² x — 5 sinx cosx + 2 = 0
Тест «Тригонометрические уравнения и неравенства»
B1. Вычислите: : arctg √3 + π/6
В 3. Найдите выражения, не имеющие смысла:
B4. Решите уравнения: а) cos 6X =0 ,б)sin(2x – π/12) =√3/2.
С 1. Решите уравнение 1 + 5 sin x cos x + 3 cos² x = 0
С 
Тест «Тригонометрические уравнения и неравенства»
B1. Вычислите: : arcsin 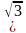
B2. Вычислите: arccos(- 1/2) — π/7
В3. Вычислите: arcctg (1/√3) — π/5
cos (π/2 + 3X) = — 1/2 ;Б) sin( x + π/4) = -1/5.
В5. Вычислить:
С 1. Решите уравнение 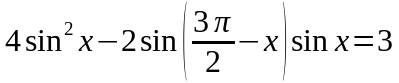
С2.Найдите множество значений t,удовлетворяющих неравенству
cos t ≥ 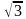
Тест «Тригонометрические уравнения и неравенства»
B1. Вычислите: 5 arccos 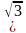
B2. Вычислите: 4 arcctg (- 1) — 3π/8
В3. Вычислите: arcctg (-√3) — π/6
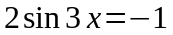
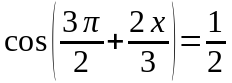
В5. Найдите 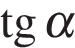
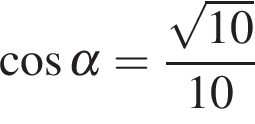
С 1. Решите уравнение 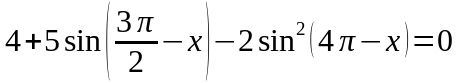
С2.Найдите множество значений t,удовлетворяющих неравенству
sin t ≥ 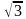
Тест «Тригонометрические уравнения и неравенства»
B1 Вычислите:
B2 Вычислите: аrccos 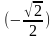
B3 Вычислите: 2 аrcsin (- 1)+ π/9
B4 Решите уравнения: а) 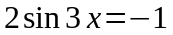
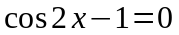
B5. Найдите 
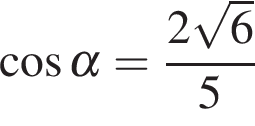
С 1. Решите уравнение 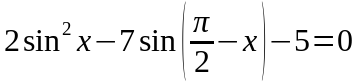
С2.Найдите множество значений t,удовлетворяющих неравенству
sin t ≥ 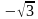
Тест «Тригонометрические уравнения и неравенства»
B1 Вычислите: 8аrccos 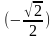
B2 Вычислите: arcctg 1/√3+ π/3 .
B3 Вычислите: 4 arcctg ( 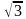
B4 Решите уравнения: а) . ; б) sin x = 0,5
B5 Найдите : , если и
С 1. Решите уравнение .
С2.Найдите множество значений t,удовлетворяющих неравенству
cos t ≥ 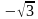
Тест «Тригонометрические уравнения и неравенства»
B1Найдите значение выражения
B2 Вычислите: -7 arcctg √3+ π/3
B3 Вычислите: arccos /2)+ 2π/3
B4 Решите уравнения: а) ; б) cos х = 1/7.
B5 Найдите значение выражения
С 1. Решите уравнение. 5 sin x + 6 cos² x-7 = 0
С2.Найдите множество значений t,удовлетворяющих неравенству
Cos2 t ≤ 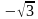
Тест «Тригонометрические уравнения и неравенства»
В1: Найдите значение выражения , если
B2 Вычислите: arcсos( -1/2) +5 аrcsin (- 1)
B3 Вычислите: : 5 arcсos( -1) +4π/9
B4 Вычислите: аrccos 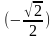
B5 Решите уравнения :а) 2 sinx + = 0; б) cos (х/2 + π/4) = — 1.
С 1. Решите уравнение. 3 sin 2 x — 4 sin x cos х + 5cos 2 х=2
С2. Решите уравнение Отобрать корни, принадлежащие отрезку
Тест «Тригонометрические уравнения и неравенства»
В1: Найдите значение выражения
B2 Вычислите: arcсos( -1) +0,5 аrcsin (- 1/2)
B3 Вычислите: : 5 arcsin( 1) +2π/3
B4 Вычислите: аrccos 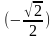
B5 Решите уравнения: а) 2 sinx + 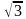
С 1. Решите уравнение. sin 2 x — 2 cos х +2+0
С2. Решите уравнение sin2x = 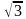
Тест «Тригонометрические уравнения и неравенства»
В1: Найдите значение выражения sin 2 x , если tg 2 х =5
B2 Вычислите: arctg( — 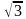
B3 Вычислите: : 2 arcsin 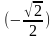
B4 Вычислите: аrccos 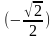
B5 Решите уравнения: а) 2 sinx — = 0; б) sin (х + π/3) = 1.
С 1. Решите уравнение. 4 sinx cosx= 4 cosx – sinx +1.
С2. Найдите множество значений t,удовлетворяющих неравенству
cos t ≥ /2 и принадлежащие промежутку [ -3 π ; -π]
Тест «Тригонометрические уравнения и неравенства»
В1. Вычислите: arcsin 1/2 — π/9
В2. Вычислите: arctg 1/√3+ π/6
В3. Вычислите: arcctg √3
В4. Решите уравнения: А)sin( x + π/4) = -1 б) cos 12x = -1
В5. Найдите выражения, не имеющие смысла:
С 1. Решите уравнение cos² x — 5 sinx cosx + 2 = 0
Тест «Тригонометрические уравнения и неравенства»
B1. Вычислите: : arctg √3 + π/6
В 3. Найдите выражения, не имеющие смысла:
B4. Решите уравнения: а) cos 6X =0 ,б)sin(2x – π/12) =√3/2.
С 1. Решите уравнение 1 + 5 sin x cos x + 3 cos² x = 0
С 2 Найти множество значений значений t,удовлетворяющих неравенству sin t /2 и принадлежащие промежутку [ — π ; 0]
Тест «Тригонометрические уравнения и неравенства»
B1. Вычислите: : arcsin 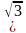
B2. Вычислите: arccos(- 1/2) — π/7
В3. Вычислите: arcctg (1/√3) — π/5
cos (π/2 + 3X) = — 1/2 ;Б) sin( x + π/4) = -1/5.
В5. Вычислить:
С 1. Решите уравнение 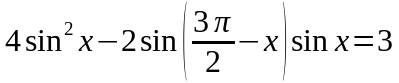
С2.Найдите множество значений t,удовлетворяющих неравенству
cos t ≥ 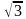
Тест «Тригонометрические уравнения и неравенства»
B1. Вычислите: 5 arccos 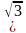
B2. Вычислите: 4 arcctg (- 1) — 3π/8
В3. Вычислите: arcctg (-√3) — π/6
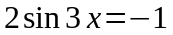
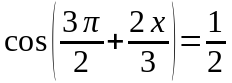
В5. Найдите 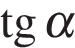
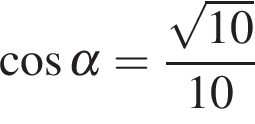
С 1. Решите уравнение 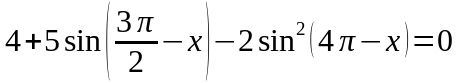
С2.Найдите множество значений t,удовлетворяющих неравенству
sin t ≥ 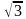
Тест «Тригонометрические уравнения и неравенства»
B1 Вычислите:
B2 Вычислите: аrccos 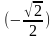
B3 Вычислите: 2 аrcsin (- 1)+ π/9
B4 Решите уравнения: а) 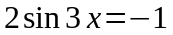
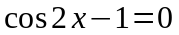
B5. Найдите 
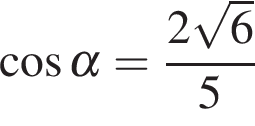
С 1. Решите уравнение 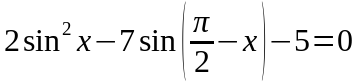
С2.Найдите множество значений t,удовлетворяющих неравенству
sin t ≥ 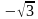
Тест «Тригонометрические уравнения и неравенства»
B1 Вычислите: 8аrccos 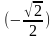
B2 Вычислите: arcctg 1/√3+ π/3 .
B3 Вычислите: 4 arcctg ( 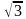
B4 Решите уравнения: а) . ; б) sin x = 0,5
B5 Найдите : , если и
С 1. Решите уравнение .
С2.Найдите множество значений t,удовлетворяющих неравенству
cos t ≥ 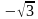
Тест «Тригонометрические уравнения и неравенства»
B1Найдите значение выражения
B2 Вычислите: -7 arcctg √3+ π/3
B3 Вычислите: arccos /2)+ 2π/3
B4 Решите уравнения: а) ; б) cos х = 1/7.
B5 Найдите значение выражения
С 1. Решите уравнение. 5 sin x + 6 cos² x-7 = 0
С2.Найдите множество значений t,удовлетворяющих неравенству
Cos2 t ≤ 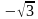
Тест «Тригонометрические уравнения и неравенства»
В1: Найдите значение выражения , если
B2 Вычислите: arcсos( -1/2) +5 аrcsin (- 1)
B3 Вычислите: : 5 arcсos( -1) +4π/9
B4 Вычислите: аrccos 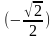
B5 Решите уравнения :а) 2 sinx + = 0; б) cos (х/2 + π/4) = — 1.
С 1. Решите уравнение. 3 sin 2 x — 4 sin x cos х + 5cos 2 х=2
С2. Решите уравнение Отобрать корни, принадлежащие отрезку
http://shkolkovo.net/theory/25
http://multiurok.ru/index.php/files/test-po-teme-trigonometricheskie-uravneniia-i-nera.html