Тригонометрические уравнения и неравенства вариант

Самостоятельная работа на 16 вариантов по теме «Тригонометрические уравнения и неравенства»

Самостоятельная работа на 16 вариантов

по теме « Тригонометрические уравнения и неравенства»

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

2 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

3 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

4 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

5 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

6 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

7 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

8 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

9 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

10 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

а)

б)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

11 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

12 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

а)

б)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

13 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

14 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

15 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

16 вариант

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа на 16 вариантов по теме «Тригонометрические уравнения и неравенства»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Самостоятельная работа на 16 вариантов

по теме « Тригонометрические уравнения и неравенства»

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

а)

б)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

а)

б)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Самостоятельная работа по теме

Тригонометрические уравнения и неравенства

1. Решите уравнения:

а)

б)

в)

г)

д)

е)

ж)

з)

2. Решите неравенства

а) б)

Краткое описание документа:

Работа состоит из 16 вариантов. Позволяет проверить основные навыки решения тригонометрических уравнений и простейших тригонометрических неравенств . Материал можно использовать в качестве индивидуального домашнего задания для подготовки к итоговой работе по решению тригонометрических уравнений.

Подходит для учащихся не только базовой группы, но и для отработки основных навыков при решении тригонометрических уравнений в профильных группах.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 932 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 682 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 308 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 573 262 материала в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.; Ч.2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.

Глава 3. Тригонометрические уравнения

Другие материалы

• 10.02.2019
• 380
• 12

• 10.02.2019
• 396
• 13

• 05.02.2019
• 182
• 1

• 01.02.2019
• 519
• 4

• 20.01.2019
• 750
• 15

• 12.01.2019
• 216
• 1

• 13.11.2018
• 356
• 2

• 13.11.2018
• 403
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 18.02.2019 7518
• DOCX 331.5 кбайт
• 218 скачиваний
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Кузнецова Екатерина Андреевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 2 года и 11 месяцев
• Подписчики: 1
• Всего просмотров: 7968
• Всего материалов: 2

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В России действуют более 3,5 тысячи студенческих отрядов

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Онлайн-конференция о создании школьных служб примирения

Время чтения: 3 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Простейшие тригонометрические уравнения (задание 5) и неравенства

\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad \mathrm\,x=b,\quad \mathrm\,x=b\) , которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb\) .

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\) ).

Рассмотрим несколько примеров:

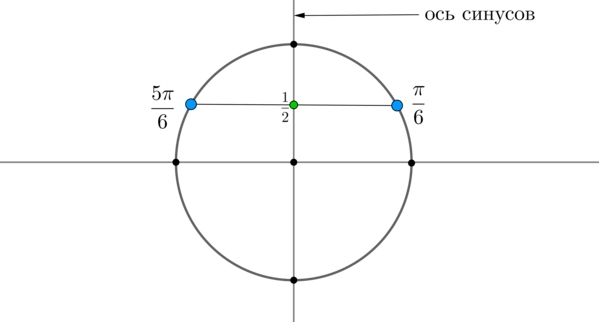
Пример 1. Решить уравнение \(\sin x=\dfrac12\) .

Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\) , где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются \(x_1=\dfrac<\pi>6+2\pi n,\ x_2=\dfrac<5\pi>6+2\pi n, \ n\in \mathbb\) .

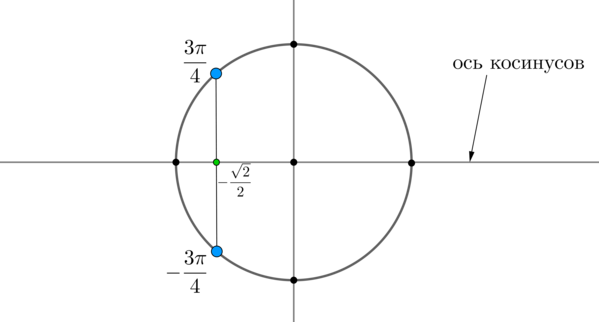
Пример 2. Решить уравнение \(\cos x=-\dfrac<\sqrt2><2>\) .

Найдем на оси косинусов точку \(-\dfrac<\sqrt2><2>\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac<\sqrt2><2>\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<3\pi>4\) и \(-\dfrac<3\pi>4\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число.

Таким образом, решением являются \(x_1=\dfrac<3\pi>4+2\pi n,\ x_2=-\dfrac<3\pi>4+2\pi n, \ n\in \mathbb\) .

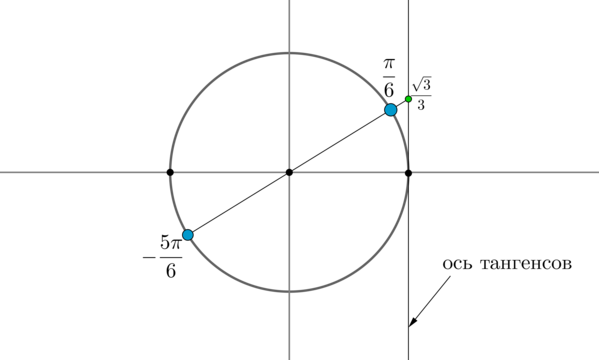
Пример 3. Решить уравнение \(\mathrm\,x=\dfrac<\sqrt3>3\) .

Найдем на оси тангенсов точку \(\dfrac<\sqrt3>3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac<\sqrt3>3\) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

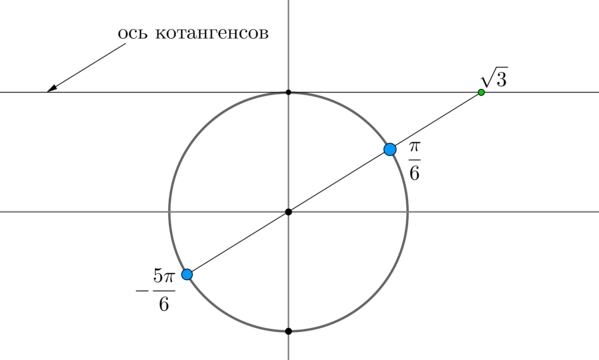
Пример 4. Решить уравнение \(\mathrm\,x=\sqrt3\) .

Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\) . Тогда в нашем случае это углы \(\dfrac<\pi>6\) и \(-\dfrac<5\pi>6\) . Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\) , где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\) .

Таким образом, решением являются \(x=\dfrac<\pi>6+\pi n, \ n\in \mathbb\) .

\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin \hline \text <Уравнение>& \text <Ограничения>& \text<Решение>\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=b & b\in \mathbb & x=\mathrm\, b+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb\) .

\(\blacktriangleright\) Любые уравнения вида \(\mathrm\,\big(f(x)\big)=a\) , (где \(\mathrm\) — одна из функций \(\sin, \ \cos, \ \mathrm,\ \mathrm\) , а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\) .

Пример 5. Решить уравнение \(\sin<(\pi x+\dfrac<\pi>3)>=1\) .

Сделав замену \(t=\pi x+\dfrac<\pi>3\) , мы сведем уравнение к виду \(\sin t=1\) . Решением данного уравнения являются \(t=\dfrac<\pi>2+2\pi n, n\in\mathbb\) .

Теперь сделаем обратную замену и получим: \(\pi x+\dfrac<\pi>3=\dfrac<\pi>2+2\pi n\) , откуда \(x=\dfrac16+2n,\ n\in\mathbb\) .

Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac<2\pi>n,\ n\in\mathbb\) , где \(\alpha\) — один из этих углов.

Рассмотрим данную ситуацию на примере:

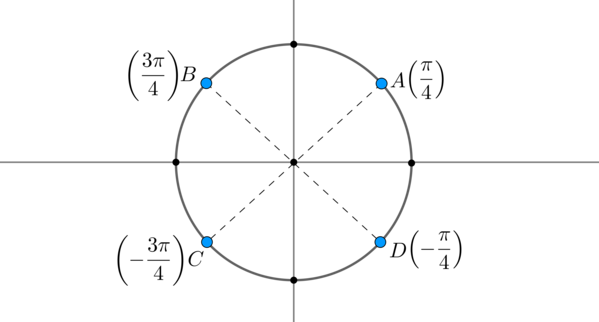
Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac<\pi>4+2\pi n, \ x_2=\pm \dfrac<3\pi>4+2\pi n, \ n\in\mathbb\) . Отметим эти точки на окружности:

Заметим, что длины дуг \(\buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over, \buildrel\smile\over\) равны \(\dfrac<\pi>2\) , то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac<\pi>4+\dfrac<\pi>2n, \ n\in\mathbb\) .

где \(\lor\) — один из знаков \(\leq,\ ,\ \geq\) .

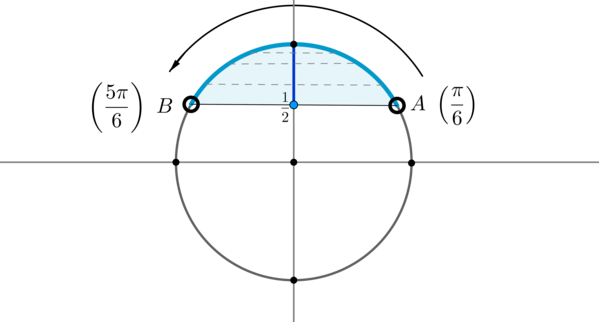
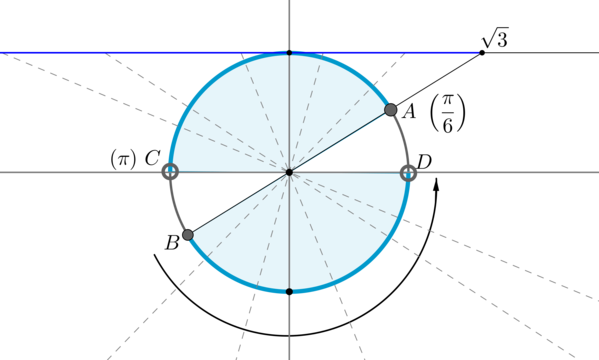
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\) .

Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, синус которых больше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>6\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>6\) , но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>6\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>6;\dfrac<5\pi>6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac<\pi>6+2\pi n;\dfrac<5\pi>6+2\pi n\right), n\in\mathbb\) , т.к. у синуса период \(2\pi\) .

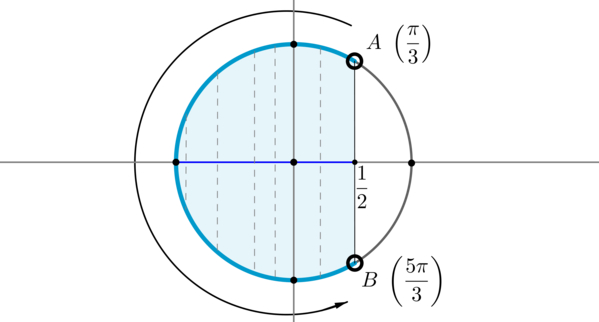
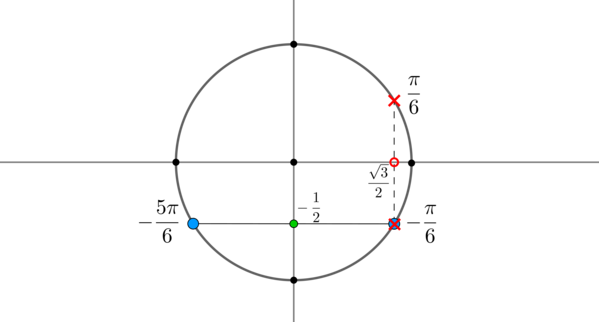
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x .

Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\) . Это точки \(A\) и \(B\) . Все точки, косинус которых меньше \(\dfrac12\) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\) , а конец — \(B\) .

Выберем в точке \(A\) любой угол, например, \(\dfrac<\pi>3\) . Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac<\pi>3\) , но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\) . Это угол \(\dfrac<5\pi>3\) . Тогда все числа из промежутка \(\left(\dfrac<\pi>3;\dfrac<5\pi>3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac<5\pi>3+2\pi n;-\dfrac<\pi>3+2\pi n\right), n\in\mathbb\) , т.к. у косинуса период \(2\pi\) .

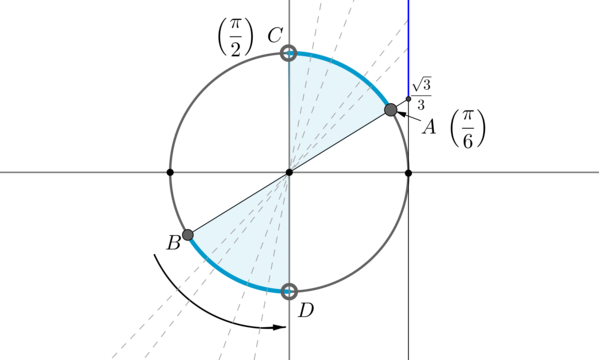
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm\, x \geq \dfrac<\sqrt<3>>3\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \dfrac<\sqrt<3>>3\) . Это точки \(A\) и \(B\) . Все точки, тангенс которых больше или равен \(\dfrac<\sqrt<3>>3\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac<\pi>2\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\dfrac<\pi>2\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\dfrac<\pi>2\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\dfrac<\pi>2+\pi n\Big), n\in\mathbb\) , т.к. у тангенса период \(\pi\) .

Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm\, x \leq \sqrt<3>\) .

Для начала отметим на окружности корни уравнения \(\mathrm\, x = \sqrt<3>\) . Это точки \(A\) и \(B\) . Все точки, котангенс которых меньше или равен \(\sqrt<3>\) , находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over\) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\) , тогда начало дуги — это угол \(\dfrac<\pi>6\) (угол должен быть меньше \(\pi\) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac<\pi>6;\pi\Big)\) . А все решения данного неравенства будут иметь вид \(\Big[\dfrac<\pi>6+\pi n;\pi+\pi n\Big), n\in\mathbb\) , т.к. период котангенса \(\pi\) .

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\) , если \(\cos x\ne \dfrac<\sqrt3>2\) .

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

Решением первого уравнения являются \(x_1=-\dfrac<\pi>6+2\pi n,\ x_2=-\dfrac<5\pi>6+2\pi n,\ n\in \mathbb\) , решением второго являются \(x\ne \pm \dfrac<\pi>6+2\pi n,\ n\in\mathbb\) . Отметим эти точки на окружности:

Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac<\pi>6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac<5\pi>6+2\pi n, n\in \mathbb\) .

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin &\sin<(\alpha+\pi n)>=\begin \sin \alpha, \text <при >n — \text< четном>\\ -\sin \alpha, \text <при >n — \text < нечетном>\end\\ &\cos<(\alpha+\pi n)>=\begin \cos \alpha, \text <при >n — \text< четном>\\ -\cos \alpha, \text <при >n — \text <нечетном>\end\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\mathrm\,(\alpha+\pi n)=\mathrm\,\alpha\\ &\sin<\left(\alpha+\dfrac<\pi>2\right)>=\cos\alpha\\ &\cos<\left(\alpha+\dfrac<\pi>2\right)>=-\sin \alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha\\ &\,\mathrm\,\left(\alpha+\dfrac<\pi>2\right)=-\,\mathrm\,\alpha \end\]

Пример 12. Решить систему \(\begin \cos x=\dfrac12\\ \sin x+\cos x>0\end\)

Решением уравнения являются \(x_1=\dfrac<\pi>3+2\pi n,\ x_2=-\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) . Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:

\(\sin x_1+\cos x_1=\dfrac<\sqrt3>2+\dfrac12>0\) , следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac<\sqrt3>2+\dfrac12 , следовательно, корень \(x_2\) нам не подходит.

Таким образом, решением системы являются только \(x=\dfrac<\pi>3+2\pi n,\ n\in\mathbb\) .

Алгебраический способ.

Пример 13. Найти корни уравнения \(\sin x=\dfrac<\sqrt2>2\) , принадлежащие отрезку \([0;\pi]\) .

Решением уравнения являются \(x_1=\dfrac<\pi>4+2\pi n, \ x_2=\dfrac<3\pi>4 +2\pi n, \ n\in\mathbb\) . Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq x_2\leq\pi\) :

\(0\leq \dfrac<\pi>4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\) . Таким образом, единственное целое значение \(n\) , удовлетворяющее этому неравенству, это \(n=0\) . При \(n=0\) \(x_1=\dfrac<\pi>4\) — входит в отрезок \([0;\pi]\) .

Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac<3\pi>4\) .

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\) .

Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\) , то есть нечетное число.

Пример: Решить уравнение \(3x+5y=2\) . Т.к. \(НОД(3,5)=1\) , то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\) :

Число \(\dfrac<2-2y>3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\) : \(0\) , \(1\) или \(2\) .
Если \(y\) при делении на \(3\) имеет остаток \(0\) , то оно записывается как \(y=3p+0\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2\cdot 3p>3=\dfrac23-2p\ne \text<целому числу>\]

Если \(y\) при делении на \(3\) имеет остаток \(1\) , то оно записывается как \(y=3p+1\) . Тогда \[\dfrac<2-2y>3=\dfrac<2-2(3p+1)>3=-2p=\text<целому числу>\]

Значит, этот случай нам подходит. Тогда \(y=3p+1\) , а \(x=\dfrac<2-2y>3-y=-5p-1\) .

Ответ: \((-5p-1; 3p+1), p\in\mathbb\) .

Перейдем к примеру:

Пример 14. Решить систему \[\begin \sin \dfrac x3=\dfrac<\sqrt3>2\\[3pt] \cos \dfrac x2=1 \end\]

Решим первое уравнение системы:

\[\left[ \begin \begin &\dfrac x3=\dfrac<\pi>3+2\pi n\\[3pt] &\dfrac x3=\dfrac<2\pi>3 +2\pi m \end \end \right.\quad n,m\in\mathbb \quad \Leftrightarrow \quad \left[ \begin \begin &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end \end \right.\quad n,m\in\mathbb\]

Решим второе уравнение системы:

\[\dfrac x2=2\pi k, k\in\mathbb \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb\]

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\) , при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\) :

\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]

Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\) , то данное уравнение не имеет решений в целых числах.

Найдем целые \(m\) и \(k\) , при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\) :

\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]

Данное уравнение имеет решение в целых числах. Выразим \(k=\frac<3m+1>2=m+\frac2\) .

Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\) .
Если \(m=2p+0\) , то \(\frac2=\frac<2p+1>2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\) , то \(\frac2=\frac<2p+1+1>2=p+1= \) целому числу.

Значит, \(m=2p+1\) , тогда \(k=3p+2\) , \(p\in\mathbb\) .

Подставим либо \(m\) , либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb\) .