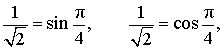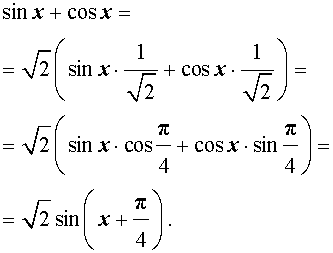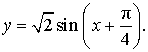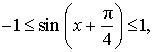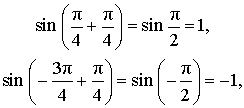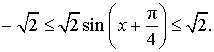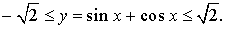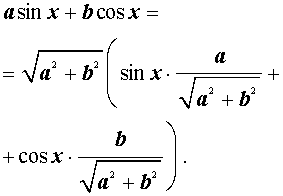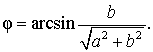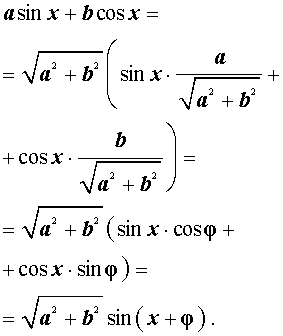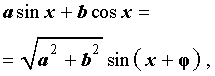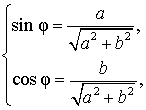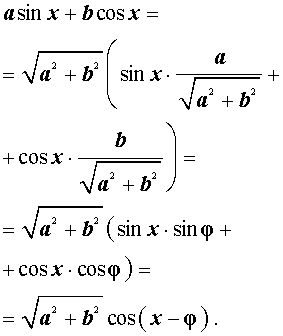Метод введения дополнительного угла (Метод введения вспомогательного аргумента)
Рассмотрим метод введения дополнительного угла на примере решения следующей задачи.
ЗАДАЧА . Найти наибольшее и наименьшее значения функции
| y = sin x + cos x. | (1) |
РЕШЕНИЕ . Заметив, что
преобразуем правую часть формулы (1):
Отсюда вытекает, что выражение (1) можно переписать в виде:
ОТВЕТ . Наибольшее значение функции (1) равно 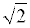
ЗАМЕЧАНИЕ . В рассмотренной задаче угол 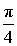
Теперь докажем формулу дополнительного угла (вспомогательного аргумента) в общем виде. Для этого рассмотрим выражение
| a sin x + bcos x | (2) |
где a и b – произвольные, отличные от нуля числа, и преобразуем его:
Введем дополнительный угол (вспомогательный аргумент) φ , у которого:
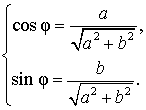 | (4) |
В случае, когда a и b являются положительными числами, в качестве дополнительного угла можно взять, например, угол
Тогда выражение (3) принимает вид:
Таким образом, мы получили формулу
которую и называют формулой дополнительного угла (вспомогательного аргумента).
Если же дополнительный угол, в отличие от формул (4), ввести по формулам
то выражение (3) примет вид
и мы получаем другой вид формулы дополнительного угла:
Метод введения вспомогательного угла
Преобразование выражения a sin х + b cos х путем введения вспомогательного угла
Лемма . Если сумма квадратов двух действительных чисел равна единице, то одно из этих чисел можно рассматривать как косинус, а другое как синус некоторого угла.
Другими словами, если а 2 + b 2 = 1, то существует угол φ, такой, что
Прежде чем доказывать эту лемму, поясним ее на следующем примере:
Поэтому существует угол φ, такой, что \( \frac<\sqrt3> <2>\) = cos φ; 1 /2 = sin φ.
В качестве φ в данном случае можно выбрать любой из углов 30°, 30° ± 360°, 30° ± 2 • 360° и т. д.
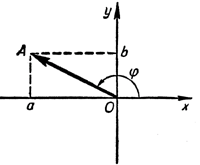
Рассмотрим вектор \(\vec<0А>\) с координатами (а, b). Поскольку а 2 + b 2 = 1, длина этого вектора равна 1. Но в таком случае его координаты должны быть равны cos φ и sin φ, где φ — угол, который образует данный вектор с осью абсцисс.
Итак, а = cos φ; b =sin φ, что и требовалось доказать.
Доказанная лемма позволяет преобразовать выражение a sin х + b cos х к более удобному для изучения виду.
Прежде всего вынесем за скобки выражение \(\sqrt
Но в таком случае
a sin х + b cos х = \(\sqrt
a sin х + b cos х = \(\sqrt
1) \( sin x + cos x = \sqrt2 (\frac<1> <\sqrt2>sin x + \frac<1><\sqrt2>cos x) = \sqrt2 (cos\frac<\pi><4>sin x + sin\frac<\pi><4>cos x ) =\\= \sqrt2(sinx + \frac<\pi><4>) \)
Полученную формулу sin x + cos x = \(\sqrt2(sinx + \frac<\pi><4>)\)полезно запомнить.
2) Если одно из чисел а и b положительно, а другое отрицательно, то выражение
a sin х + b cos х удобнее преобразовывать не к синусу суммы, а к синусу разности двух углов. Так,
$$ 3sinx — 4cosx = \sqrt<9+16>(\frac<3><\sqrt<9+16>>sinx — \frac<4><\sqrt<9+16>>cosx) =\\= 5(sinx\cdot\frac<3> <5>— cosx\cdot\frac<4><5>) = 5sin(x — \phi), $$
где под φ можно подразумевать любой угол, удовлетворяющий условиям:
В частности, можно положить φ = arctg 4 /3. Тогда получим:
3 sin х — 4 cos x = 5 sin (x — arctg 4 /3).
Тема 19. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Введение вспомогательного аргумента. Методы замены неизвестного. Способ преобразования произведения тригонометрических функций в сумму.
материал для подготовки к егэ (гиа) по алгебре (10 класс) по теме
Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным экзаменам по математике в вузы, проводимым как в форме письменных контрольных работ, так и в форме тестирований.
Имея многолетний положительный опыт подготовки школьников и абитуриентов к экзаменам по математике, проводимым в разных формах, считаю целесообразным поделиться своими разработками со всеми заинтересованными в них лицами.
Тема 19. «Тригонометрические уравнения. Введение вспомогательного аргумента. Методы замены неизвестного. Способ преобразования произведения тригонометрических функций в сумму» содержит теоретические сведения, систематизированный набор ключевых методов решения типовых задач, сопровождающихся подробным разбором решений. По каждому методу приводятся упражнения с ответами для закрепления изучаемого материала.
Материал будет полезен для использования учителями общеобразовательных учреждений на элективных курсах и факультативных занятиях по математике для подготовки учащихся к ЕГЭ, абитуриентов при подготовке к вступительным экзаменам в вузы.
Скачать:
| Вложение | Размер |
|---|---|
| tema_19._trigonometricheskie_uravneniya.metody_resheniya_7-9.docx | 83.21 КБ |
Предварительный просмотр:
Тема 19. Тригонометрические уравнения.
Введение вспомогательного аргумента. Методы замены неизвестного.
Способ преобразования произведения тригонометрических функций в сумму.
VII. Введение вспомогательного аргумента.
Этим методом решаются уравнения вида
Уравнение решается по следующему плану:
1) записываем уравнение в виде
Соответствующее значение существует, т.к. выполнено характеристическое свойство
3) уравнение принимает вид то есть — это простейшее уравнение.
Примеры. Решить уравнение.
Решение: тогда Перепишем исходное уравнение в виде . Далее необходимо учесть, что тогда рассматриваемое уравнение можно записать в виде а затем с помощью формулы синуса суммы перейти к уравнению
Тогда уравнение перепишем в виде
Полагая , приходим к уравнению
Так как (или ), то ( ).
- Найти число корней уравнения на интервале
Подсчитаем число корней, принадлежащих интервалу При
При и корни не принадлежат интервалу следовательно, число корней равно 4.
VIII. Методы замены неизвестного (подстановка).
Применение некоторых замен неизвестного приводит к упрощению соответствующих уравнений.
Примеры. Решить уравнение.
Решение. Сделаем замену, обозначив . Выразим из этой замены , получим . Итак, подставив в уравнение выражения и , получим квадратное уравнение . Следовательно, . Первое уравнение совокупности не имеет решений, так как Решим второе уравнение совокупности.
Замечание . Если тригонометрическое уравнение содержит разность синуса и косинуса и их произведение, то используют замену ,
Решение. Воспользуемся формулой и перепишем данное уравнение иначе
Обозначим . Получаем . Тогда . Второе уравнение совокупности решений не имеет. Решим
- Ответ:
- Ответ:
Ответ:
IX. Способ преобразования произведения тригонометрических функций в сумму.
Сущность способа поясним на примерах.
Пример. Решить уравнение
Решение. Применим к обеим частям уравнения формулу получим Воспользуемся формулой Получим
- Ответ:
- Ответ:
- Число корней уравнения на интервале равно.
http://razdupli.ru/teor/78_metod-vvedeniya-vspomogatelnogo-ugla.php
http://nsportal.ru/shkola/algebra/library/2014/04/04/tema-19-trigonometricheskie-uravneniya-vvedenie-vspomogatelnogo