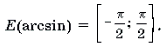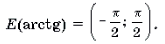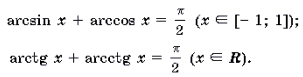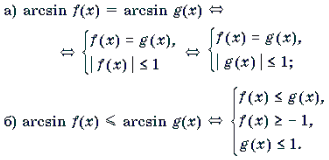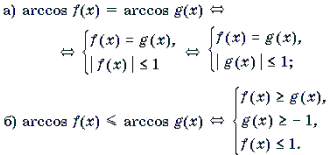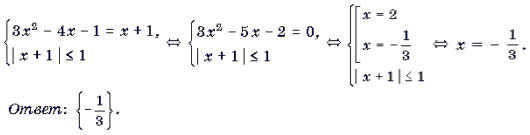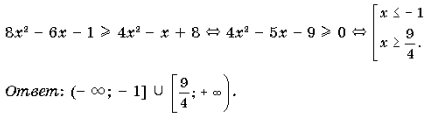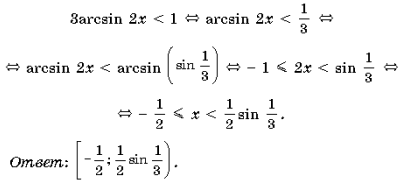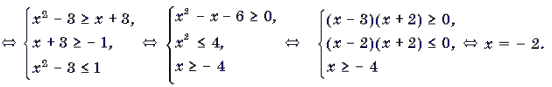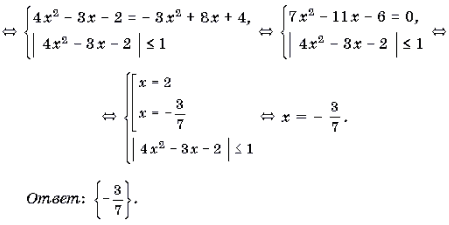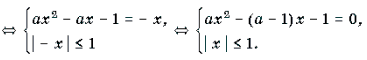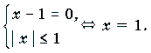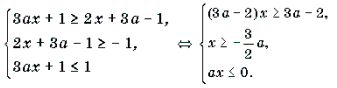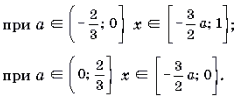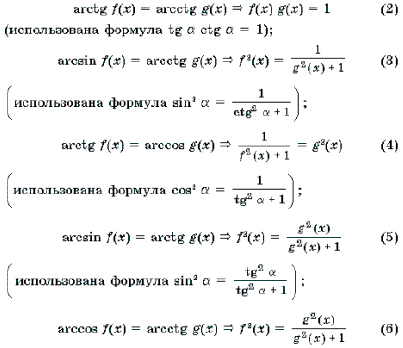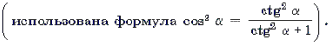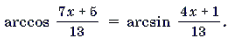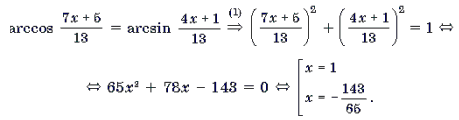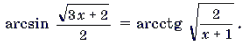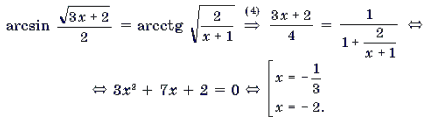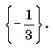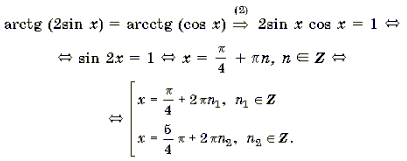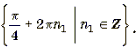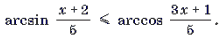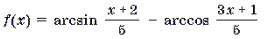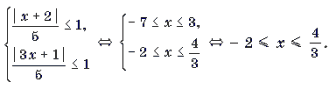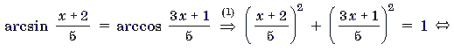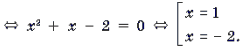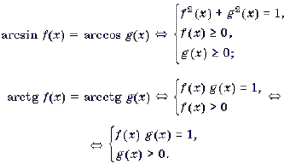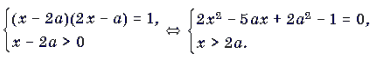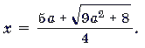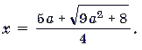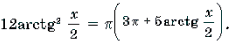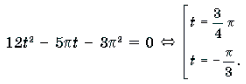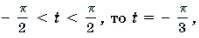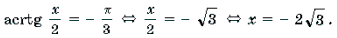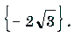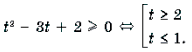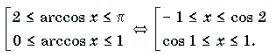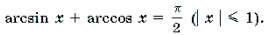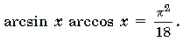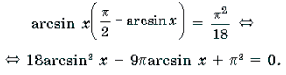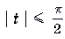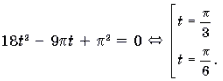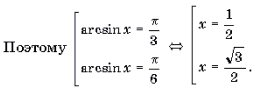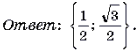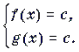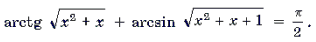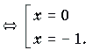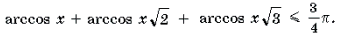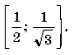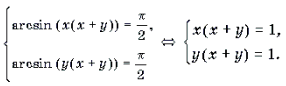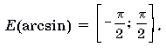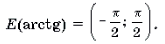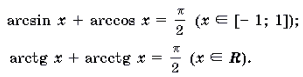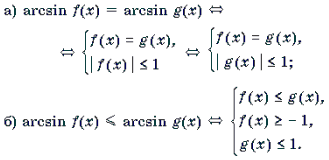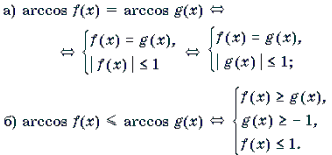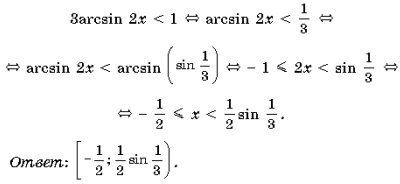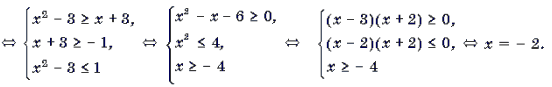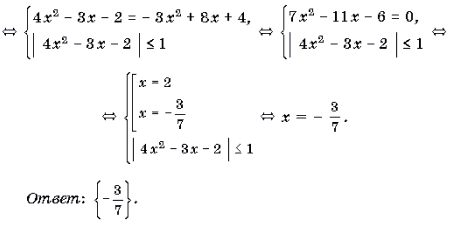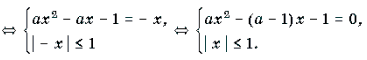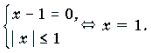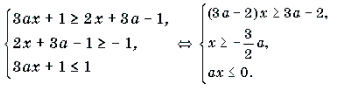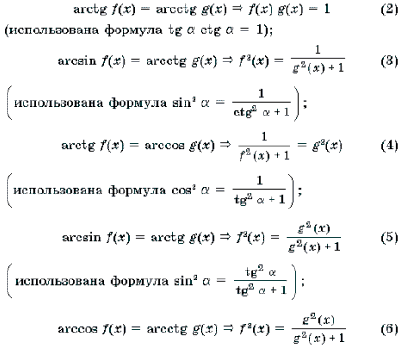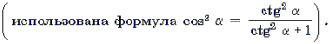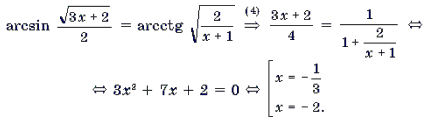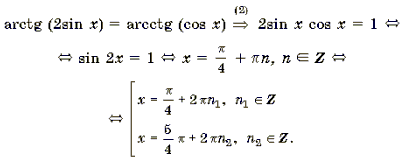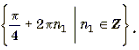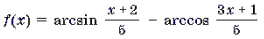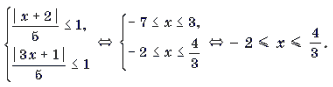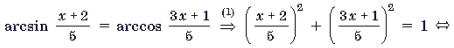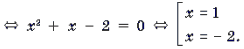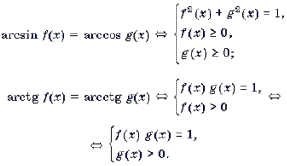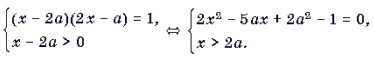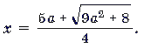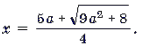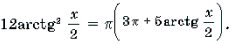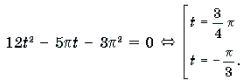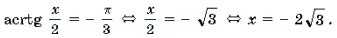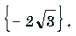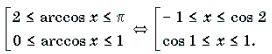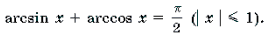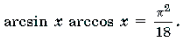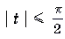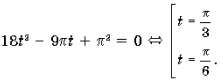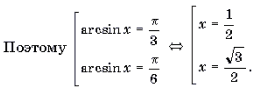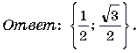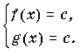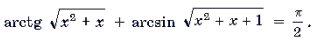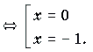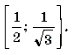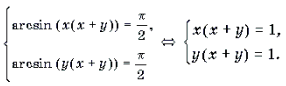Тригонометрические уравнения содержащие обратные тригонометрические функции

Уравнения и неравенства, содержащие обратные тригонометрические функции

Задачи, связанные с обратными тригонометрическими функциями, часто вызывают у школьников старших классов значительные трудности. Связано это, прежде всего, с тем, что в действующих учебниках и учебных пособиях подобным задачам уделяется не слишком большое внимание, и если с задачами на вычисление значений обратных тригонометрических функций учащиеся еще как-то справляются, то уравнения и неравенства, содержащие эти функции, нередко ставят их в тупик. Последнее не удивительно, поскольку практически ни в одном учебнике (включая учебники для классов с углубленным изучением математики) не излагается методика решения даже простейших уравнений и неравенств такого рода. Предлагаемая вашему вниманию статья посвящена методам решения уравнений и неравенств, содержащих обратные тригонометрические функции. Надеемся, что она окажется полезной для учителей, работающих в старших классах – как общеобразовательных, так и математических.

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);

4 Функция y = arcctg x определена и монотонно убывает на R;

Свойства монотонности и ограниченности являются ключевыми при решении многих уравнений и неравенств, содержащих обратные тригонометрические функции. Перейдем к рассмотрению методов решения этих уравнений и неравенств.

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

Решение уравнений и неравенств, левая и правая части которых представляют собой одноименные обратные тригонометрические функции различных аргументов, основывается, прежде всего, на таком свойстве этих функций, как монотонность. Напомним, что функции y = arcsin t и y = arctg t монотонно возрастают, а функции y = arccos t и y = arcctg t монотонно убывают на своих областях определения. Поэтому справедливы следующие равносильные переходы.

1 .

2 .

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

2) a № 0. В этом случае уравнение системы является квадратным. Его корни: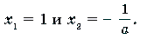
Так как | x | Ј 1, то 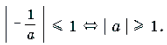. Если a = – 1, то x₂ = x₁ = 1. Если a О (– Ґ Ч ; – 1) И [1; Ґ ), то уравнение имеет два корня.

Ответ: при 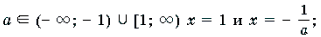при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

Решение. Неравенство равносильно системе

Решать последнюю систему можно графо-аналитическим методом, учитывая то, что при a > первое неравенство системы равносильно неравенству x і 1, при a – неравенству x Ј 1, при a = решением первого неравенства является любое действительное число. Множество всех точек (x; a) плоскости Oxa, удовлетворяющих системе, показано на рис. 1 штриховкой.

Ответ: при | a | > решений нет; при a = – x = 1;

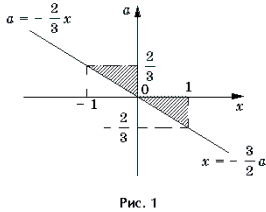
II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами. Эта группа задач является чуть более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Рассуждения здесь могут быть примерно следующими. Пусть требуется решить уравнение arcsin f(x) = arccos g(x). Предположим, что x₀ – решение этого уравнения. Обозначим arcsin f(x₀) = arccos g(x₀) через a. Тогда sin a = f(x₀), cos a = g(x₀), откуда f 2 (x₀) + g 2 (x₀) = 1. Итак, arcsin f(x) = arccos g(x) Ю f 2 (x) + g 2 (x) = 1. (1)

Рассуждая аналогично, можно получить следующие переходы:

Замечание 3. Корнем каждого из уравнений (1)–(4) может быть только такое число x₀, для которого f(x₀) і 0 и g(x₀) і 0. В противном случае множество значений левой и правой частей уравнения не пересекаются.

Пример 9. Решить уравнение

Корень 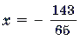является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

Ответ: .

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида 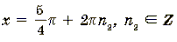являются посторонними.

Ответ:

При решении неравенств, левая и правая части которых представляют собой разноименные обратные тригонометрические функции, целесообразно использовать метод интервалов, а в некоторых случаях учитывать свойства монотонных функций.

Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

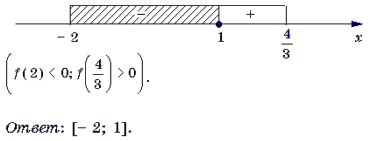
Корень x = – 2 является посторонним.

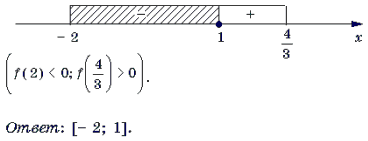
3) Решим неравенство f(x) Ј 0 методом интервалов.

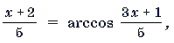
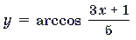
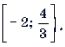
Замечание 4. Заметим, что найдя корень уравнения можно было не обращаться к методу интервалов, а воспользоваться тем, что функция является монотонно возрастающей, а функция монотонно убывающей на отрезке . Поэтому решением исходного неравенства является промежуток [– 2; 1]. Следует, однако, понимать, что метод интервалов является более универсальным, – ведь его можно применять и в тех случаях, когда использование свойств монотонных функций не приводит к искомому результату.

При решении уравнений и неравенств данного типа, содержащих параметры, становится актуальным вопрос о равносильности преобразований. Чтобы преобразования (1)–(4) сделать равносильными, следует учесть естественные ограничения, связанные с областями определения обратных тригонометрических функций и множествами их значений (см. замечание 3). Так, например,

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Графиком квадратного трехчлена f(x) = 2x 2 – 5ax + 2a2 – 1 является парабола, ветви которой направлены вверх. Поскольку f(2a) = – 1 2a. Это корень

Ответ: при любом a

III. Замена переменной

Некоторые уравнения и неравенства, содержащие обратные тригонометрические функции, можно свести к алгебраическим, сделав соответствующую замену переменной. При этом следует помнить о естественных ограничениях на вводимую переменную, связанных с ограниченностью обратных тригонометрических функций.

Пример 14. Решить уравнение

Решение. Обозначим 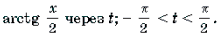После преобразований получим уравнение

Поскольку

откуда

Ответ:

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда

Поскольку 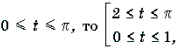откуда

Ответ: [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t,

Тогда

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Решение некоторых уравнений и неравенств, содержащих обратные тригонометрические функции, основывается исключительно на таких свойствах этих функций, как монотонность и ограниченность. При этом используются следующие теоремы.

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 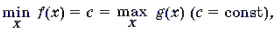то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

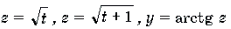
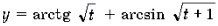
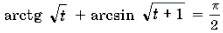
Функции являются монотонно возрастающими. Поэтому функция также является монотонно возрастающей. В силу теоремы 1 уравнение имеет не более одного корня. Очевидно, что t = 0 является корнем этого уравнения. Поэтому x 2 + x = 0

Пример 19. Решить неравенство

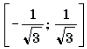
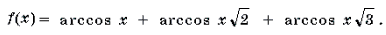
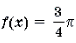
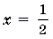
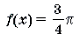
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок

Ответ:

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

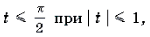
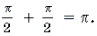
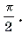
Решение. Поскольку arcsin то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе:

Решение последней системы не представляет труда.

Тригонометрические уравнения содержащие обратные тригонометрические функции

Вначале напомним важнейшие свойства обратных тригонометрических функций.

1 Функция y = arcsin x определена и монотонно возрастает на отрезке [– 1; 1];

arcsin (– x) = – arcsin x (x О [– 1; 1]);

2 Функция y = arccos x определена и монотонно убывает на отрезке [– 1; 1];

3 Функция y = arctg x определена и монотонно возрастает на R;

arctg (– x) = – arctg x (x О R);

4 Функция y = arcctg x определена и монотонно убывает на R;

I. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями

1 .

2 .

3 .

4 .

Замечание 1. Какой из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: | f(x) | Ј 1 (тогда используем первую систему), или | g(x) | Ј 1 (в этом случае используем вторую систему).

Пример 1. Решить уравнение arcsin (3x 2 – 4x – 1) = arcsin (x + 1).

Решение. Уравнение равносильно системе

Замечание 2. Решать неравенство, входящее в систему, вообще говоря, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении примера 1.

Пример 2. Решить неравенство arcctg (8x 2 – 6x – 1) Ј arcctg (4x 2 – x + 8).

Решение. Неравенство равносильно следующему:

Пример 3. Решить неравенство 3arcsin 2x

Пример 4. Решить неравенство arccos (x 2 – 3) Ј arccos (x + 3).

Пример 5. Решить уравнение arccos (4x 2 – 3x – 2) + arccos (3x 2 – 8x – 4) = p .

Решение. Так как p – arccos t = arccos (– t), то имеет место следующая цепочка равносильных преобразований:

arccos (4x 2 – 3x – 2) = p – arccos (3x 2 – 8x – 4) Ы
Ы arccos (4x 2 – 3x – 2) = arccos (– 3x 2 + 8x + 4) Ы

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 7. Решить уравнение с параметром a: arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

Рассмотрим два случая:

1) a = 0. В этом случае система примет вид:

Ответ : при при a = – 1 и a = 0 x = 1; при прочих a решений нет.

Пример 8. Решить неравенство с параметром a: arccos (3ax + 1) Ј arccos (2x + 3a – 1).

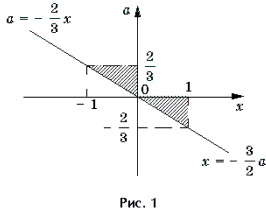
Решение. Неравенство равносильно системе

Ответ: при | a | > решений нет; при a = – x = 1;

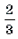
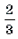
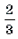
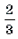
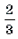
II. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями

Рассуждая аналогично, можно получить следующие переходы:

Пример 9. Решить уравнение

Корень является посторонним.

Пример 10. Решить уравнение

Корень x = – 2 является посторонним.

Ответ : .

Пример 11. Решить уравнение arctg (2sin x) = arcctg (cos x).

Корни вида 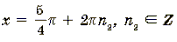являются посторонними.

Ответ :

Пример 12. Решить неравенство

Решение. Рассмотрим функцию

и решим неравенство f(x) Ј 0 методом интервалов.

1) Найдем D(f). Для этого решим систему

2) Найдем нули f(x). Для этого решим уравнение

Корень x = – 2 является посторонним.

3) Решим неравенство f(x) Ј 0 методом интервалов.

Пример 13. Решить уравнение с параметром a: arcctg (x – 2a) = arctg (2x – a).

Решение. Данное уравнение равносильно системе

Ответ: при любом a

III. Замена переменной

Пример 14. Решить уравнение

Решение. Обозначим 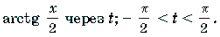После преобразований получим уравнение

Поскольку

откуда

Ответ :

Пример 15. Решить неравенство arccos 2 x – 3arccos x + 2 і 2.

Решение. Пусть arccos x = t, 0 Ј t Ј p . Тогда

Поскольку 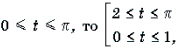откуда

Ответ : [– 1; cos 2] И [cos 1; 1].

Иногда свести уравнение или неравенство к алгебраическому можно с помощью тождества

Пример 16. Решить уравнение

Решение. Данное уравнение равносильно следующему:

Пусть arcsin x = t,

Тогда

IV. Использование свойств монотонности и ограниченности обратных тригонометрических функций

Теорема 1. Если функция y = f(x) монотонна, то уравнение f(x) = c (c = const) имеет не более одного решения.

Теорема 2. Если функция y = f(x) монотонно возрастает, а функция y = g(x) монотонно убывает, то уравнение f(x) = g(x) имеет не более одного решения.

Теорема 3. Если 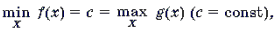то на множестве X уравнение f(x) = g(x) равносильно
системе

Пример 17. Решить уравнение 2arcsin 2x = 3arccos x.

Решение. Функция y = 2arcsin 2x является монотонно возрастающей, а функция y = 3arccos x – монотонно убывающей. Число x = 0,5 является, очевидно, корнем данного уравнения. В силу теоремы 2 этот корень – единственный.

Пример 18. Решить уравнение

Решение. Пусть x 2 + x = t. Тогда уравнение примет вид

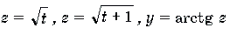
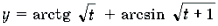
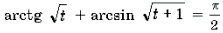
Пример 19. Решить неравенство

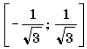
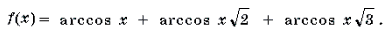
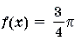
Решение. Левая часть неравенства представляет собой монотонно убывающую на отрезке функцию Уравнение в силу теоремы 1 имеет не более одного корня. Очевидно, что – корень этого уравнения. Поэтому решением неравенства является отрезок

Ответ :

Пример 20. Решить уравнение arcsin (x(x + y)) + arcsin (y(x + y)) = p .

Решение. Поскольку arcsin 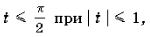то левая часть уравнения не превосходит Знак равенства возможен, лишь если каждое слагаемое левой части равно . Таким образом, уравнение равносильно системе:

Решение последней системы не представляет труда.

Уравнения и неравенства, содержащие обратные тригонометрические функции

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Обратные тригонометрические функции

Уравнения и неравенства

В данном материале уравнения и неравенства, содержащие обратные тригонометрические функции, по методам решения условно разделены на 4 группы, поэтому изложение материала производится в соответствии этого разбиения. Вначале перечислены основные свойства обратных тригонометрических функций и основные соотношения, которые используются при решении уравнений. В конце имеется набор упражнений для самостоятельной работы и приведены ответы.

Вначале напомним важнейшие свойства обратных тригонометрических функций.

Функция у = arcsin x

E(arcsin) = [- π /2;π /2]

arcsin 0 = 0, arcsin 1 = π /2,

является функцией нечетной, т.е.

arcsin(-x) = arcsin x; (| х |  1)

является функцией возрастающей

Функция у = arccos x

arccos 0 = π /2, arccos 1 = 0,

4) не является функцией ни четной, ни нечетной: arccos (-x) = π – arccos x; (|х |  1)

5) является функцией убывающей.

Функция у = arctg x

arctg 0 = 0, arctg  2/2 = π/4;

является функцией нечетной:

arctg (-x) = — arctg x;

является функцией возрастающей.

Функция у = arcctg x

Не является функцией ни четной, ни нечетной: arcctg(-x) = π – arcctg x

Является функцией убывающей.

sin(arcsin x) = x, при -1  x  1;

cos(arccos x) = x, при -1  x  1;

tg(arctg x) =x, при x  R

ctg(arcctg x) =x, при x  R

Формулы перехода к функциям другого наименования:

arcsin x = arccos = arctg x/ = arcctg /x, 0

arccos x = arcsin = arctg /x = arcctg x/ , 0

arctg x = arcsin x/ = arccos 1/ = arcctg 1/x, x>0

arcctg x = arcsin 1/ = arccos x/ = arctg 1/x, x>0

3. Основные тождества:

arcsin x + arccos x =π /2, при -1  x  1

arctg x + arcctg x = π /2 , при x  R

Применение метода замены переменной

Пример 1. Решить уравнение

2 arcsin 2 x – 7 arcsin x + 3 =0

Пусть arcsin x =t, | t |  π / 2

Откуда t = 3 или t = 1/2

Поскольку , | t |  π / 2 , то t = 1/2

Или arcsin x = 1/2 , x = sin1 / 2

Пример 2. Решить уравнение

arcsin 2 x + arccos 2 x = 5π 2 /36.

Пусть arcsin x =α, arccos x =β, | α |  π/2, 0  β  π;

По условию задания составим систему двух уравнений:

α 2 + β 2 = 5π 2 /36,

Решая, систему двух уравнений с двумя неизвестными получаем что, β = π /3 или β = π / 6

Или arccos x = π /3 или arccos x = π / 6

x = 1 / 2 или х =  3 / 2

Пример 3. Решить неравенство

arccos 2 x – 3 arccos x + 2  2

Решение. Пусть arccos x = t, 0  t  π. Тогда

Решая, квадратичное неравенство имеем:

Поскольку 0  t  π , то  2  t  π

Откуда  2  arccos x  π   — 1  x  cos 2

 0  arccos x  1  cos 1  x  1.

Ответ : [-1; cos 2]  [cos 1; 1].

Решить следующие уравнения методом замены переменной:

arcsin 2 x – π /2arcsin x + π 2 /18 = 0

arctg 2 x + arcctg 2 x = π 2 /8

6 arctg 2 x – 5 arctg x + 1 = 0

12 arctg 2 x/2 = π (3 π + 5 arctg x/2)

arcsinx  arccosx = π 2 /18

arctgx  arcctgx = -5π 2 /18

2. Уравнения и неравенства, содержащие одноименные обратные тригонометрические функции

Решение этих уравнений и неравенств основывается на таком свойстве обратных тригонометрических функций, как монотонность. Напомним, что функции y = arcsin x и y = arctg x монотонно возрастают, а функции y = arccos x и y = arcctg x монотонно убывают. Поэтому справедливы следующие равносильные переходы:

a) arcsin f(x) = arcsin g(x) 

б ) arcsin f(x)  arcsin g(x)   f(x)  -1,

а ) arccos f(x) = arccos g(x) 

б ) arccos f(x)  arccos g(x)   g(x)  -1,

3 . а ) arctg f(x) = acrtg g(x)  f(x) = g(x);

б ) arctg f(x)  arctg g(x)  f(x)  g(x).

4. а ) arcctg f(x) = accrtg g(x)  f(x) = g(x);

б ) arcctg f(x)  arcctg g(x)  f(x)  g(x).

Замечание. Какое из двух равносильных систем пользоваться при решении уравнений 1а) и 2а), зависит от того, какое неравенство проще: |f(x)|  1 (тогда используем первую систему), или |g(x) |  1 (в этом случае используем вторую систему).

Пример 10. Решить неравенство

2 arcsin x/2  π /3

arcsin x/ 2  π /6

arcsin x/ 2  arcsin 1/ 2

С учетом ОДЗ –2  х  1

Пример 11. Решить уравнение

arcsin (2x -15) = arcsin (x 2 — 6x — 8)

Учитывая, вышеприведенные равносильные преобразования имеем:

2х – 15 = х 2 – 6х – 8,   x 2 – 8x + 7 – 0, 

| 2x – 15|  1  | 2x – 15 |  1

Замечание. Решать неравенство, входящее в систему, не обязательно. Достаточно проверить, удовлетворяют ли неравенству найденные корни уравнения, как это и было сделано при решении уравнения 11.

Пример 12. Решить уравнение

arccos (4x 2 – 3x – 2) + arccos ( 3x 2 – 8x – 4) = π.

Решение. Так как π – arccos t = arccos (-t ), то имеет место следующая цепочка равносильных преобразований:

arccos ( 4x 2 – 3x – 2) = π – arccos ( 3x 2 – 8x – 4) 

arccos ( 4x 2 – 3x – 2) = arccos (-3x 2 + 8x + 4) 

 4x 2 – 3x – 2 = -3x 2 + 8x + 4,   7x 2 – 11x – 6 – 0,  |4x 2 – 3x – 2 |  1  |4x 2 – 3x – 2 |  1

Пример 13. Решить неравенство

arctg (5x 2 – 3x) > arctg (5x – 3).

Это неравенство равносильно неравенству:

( 5x 2 – 3x) > (5х – 3),

х (5х – 3) – (5х – 3) > 0,

Решение находится за корнями:

x > 1 или x  ; 0,6)  (1;  ).

Пример 14. Решить неравенство

arcsin (x 2 – x) > arcsin (3x – 4).

Это неравенство равносильно системе неравенств:

Решим первое неравенство системы:

Решим второе неравенство системы:

(1 —  5)/2  х  (1 +  5)/2.

Решим третье неравенство системы: х  1.

Объединяя, полученные результаты имеем

Аналогичные равносильные преобразования используются и при решении задач с параметрами.

Пример 15. Решить уравнение с параметром а:

arcsin (ax 2 – ax + 1) + arcsin x = 0.

Решение. Уравнение равносильно уравнению

arcsin (ax 2 – ax + 1) = — arcsin x 

 arcsin (ax 2 – ax + 1) = arcsin (-x) 

 ax 2 – ax + 1 = -1,   ax 2 – (a – 1)x – 1 = 0,

Рассмотрим два случая:

а =0. В этом случае система примет вид:

а  0. В этом случае уравнение системы является квадратным. Его корни: х₁ = 1 и х₂ = -1/a. Так как |x |  1, то | -1/a |  1  |a |  1. Если а = -1, то х₂ = х₁ = 1.

Если а  ( —  ; -1)  [1;  ), то уравнение имеет два корня.

Ответ: при а  (-  ; -1)  [1;  ) х = 1 и х = — 1/a;

при а = -1 и а = 0 х = 1;

при прочих а решений нет.

Решить следующие уравнения и неравенства:

16. 2 arccos x/2 ≥ π /2.

17. arccos (x 2 – 4x +3) > π /2.

18. arcsin (2x 2 – 9x +8 )/2 π /6

19. arcsin (5x – 3) π /3

20. arccos (3x + 2) = arccos ( 5x + 3).

21. arcctg (x 2 +2x) = arcctg (8x –5)

22. arccos (2x –1) arcsin (5x –3)

24. arctg x/2 + arctg x/3 = arctg x

3. Уравнения и неравенства, содержащие разноименные обратные тригонометрические функции.

При решении уравнений и неравенств данного вида пользуются известными тригонометрическими тождествами. Эта группа задач является более сложной по сравнению с предыдущей. При решении многих уравнений такого рода бывает целесообразно не обсуждать вопрос о равносильности преобразований, а сразу переходить к уравнению-следствию и после его решения делать необходимую проверку. Например, требуется решить уравнение

arcsin f(x) = arccos g(x).

Предположим, что х₀ – решение этого уравнения. Обозначим arcsin f(х₀) = arccos g(х₀) через α. Тогда sin α = f(х₀), cos α = g(х₀), откуда

arcsin f(x) = arccos g(x)  f 2 (х₀) + g 2 (х₀) = 1.

Пример 25. Решить уравнение:

arcsin 5x = arccos 12x

Решение. Используем формулу:

arcsin f(x) = arccos g(x)   f 2 (х₎ + g 2 (х) = 1,

Условия f(x)  0, g(x)  0 появляются так, как в противном случае, множество значений правой и левой частей уравнения не пересекаются.

Исходя, из вышеприведенной системы имеем:

(5х) 2 + (12х) 2 = 1,   25х 2 + 144 х 2 = 1, 

169х 2 = 1,  х = ± 1/13,

Пример 26. Решить неравенство

arccos x > arctg x.

Решение. Решим неравенство методом интервалов. Рассмотрим функцию f(x) = arccos x – arctg x и решим неравенство f(x) > 0. Областью определения этой функции является отрезок [-1;1]

Найдем нули функции: arccos x = arctg x

Используя формулу cos 2  = 1/(1 + tg 2  ) перейдем к системе:

x > 0; так как множество значений функций

y = arccos x и y = arc t g x совпадают при x > 0.

Решением первого уравнения системы будут значения х 2 = (  5 – 1)/2, но т.к. x > 0, то остается один нуль: х =  (  5 – 1)/2. Отметим его на координатной прямой:

Определим знаки в каждом интервале:

f(1) = arccos 1 – arctg 1 = — π /4

f(-1) = arccos(-1) – arctg(-1) = π + π /4 >0;

f(x) > 0 при -1  x  (  5 – 1)/2.

Пример 27. Решить уравнение

arcsin x = arccos(1 –2x).

Решение. Исходному уравнению равносильна система  sin(arcsin x) = sin(arccos(1 – 2x)),

Отсюда  х =  1 – (1 – 2х) 2 ,

Решить уравнения и неравенства:

28. arccos 4x = arcsin 3x;

29. arcsin x = arccos √1-x;

30. arcsin (x 2 – 2x) = arccos √1-x 2 ;

31. arcsin x = arcctg x;

Общий метод решения.

При решении уравнений и неравенств этого типа используются методы сведения их к алгебраическим. При их решении приходится использовать самые разные преобразования (которые могут быть не эквивалентными), поэтому необходимо сделать проверку каждого получившегося корня.

Пример 34. Решить неравенство

arcsinx ( π /2 – arcsin x )  0.

Решение. ОДЗ: | x |  1

Пусть arcsin x = t , | t |  π /2

Тогда неравенство перепишется

Данное неравенство равносильно совокупности:

С учетом условия | t |  π /2

-π/2  t  0, t = π /2

Вернемся к старой переменной:

— π /2  arcsin x  0, arcsin x = π/2

Пример 35. Решить уравнение

arccos x = 2 arctg (1 – x ).

Решение. ОДЗ: | x |  1

Обозначим arccos x через α , а arctg (1 – х) через β, тогда cos α = x , tg β = 1 – x . По условию задачи имеем систему:

Преобразуем второе уравнение системы:

Заменим tg  = t, тогда 1 – t 2 + t + t 3 – 1 – t 2 = 0,

t 3 – 2t 2 + t = 0,

 t = 0,   tg  = 0,   1 – x = 0,   x = 1,

 t = 1;  tg  = 1;  1 – x = 1;  x = 0.

Пример 36. Решить уравнение

arcsin (1 + 2 cos x ) + arccos (1 + 3 tg x ) = π /2.

Решение: Перепишем уравнение в виде:

arcsin(1 + 2cos x) = (π/2 — arccos(1 + 3tg x)),

Возьмем синусы обеих частей :

sin(arcsin(1 + 2cos x)) = sin(π/2 — arccos(1 + 3tg x)),

1 + 2cos x = 1 + 3tg x,

2 cos x – 3 tg x = 0,

2 cos 2 x – 3sin x = 0,

2 – 2 sin 2 x – 3sin x = 0,

2 sin 2 x + 3sin x – 2 = 0,

2 t 2 + 3 t – 2 = 0,

т.к. |t |  1, то t = 2 – посторонний корень,

следовательно t = 1/ 2;

x = 5π/6 + 2πn, n  Z

Проверка показывает, что серия корней

x = π/6 + 2πn, является посторонней.

Ответ: x = 5π/6 + 2πn, n  Z.

Решить уравнения и неравенства:

37. arcsin x = 2 arctg2x/3;

38. arcsin (x 2 – 3x + 0,5) = π /6;

39. arcsin (x 2 –2x +2) = π x /2;

40. arcsin 2x = 3 arcsin x;

41. arccos(x –1) = 2 arccos x;

42. arccos(3x – 4) = 2arctg(5 – 3x);

43. arcsin 2x + arccos(6x –2)  0;

В этом разделе представлены разные примеры, которые можно использовать как на уроках, так и при подготовке при поступлении в вузы.

Решить уравнение ( неравенство, систему).

44. arcsin ( x + 1) + arccos ( x – 1) = π /2;

45. arcsin(x + 1/x) + arctg(x 2 –1) = π/3;

46. arcsin 1/  x + arccos  (1-x) = π/2;

47. arcsin2x + arccos 2 x = π 2 /2;

48. arctg 3 x +arcctg 3 x = π 3 /24;

49. 3arctgx + 2arcctgx = π;

50. arcsin(1 – x) – 2arcsinx = π/2;

51. arctg(x 2 + 1) + arctg(x 2 –1) = π/4;

52. arcsin2x = 3arcsinx;

53. arctg(x –1)/x = 2arctg(x –1);

54. arcsin x + arcsin2x = π/2;

55.  arcsin x  arcsin y = π 2 /18,

 arccos x + arccos y = π/2;

56.  arcsin x + arccos y = π/2,

57.  arctg x + arctg y = π/3,

58.  arcsin x  arccos x = π 2 /18,

59.  arctg x  arcctg x = π 2 /16,

60.  arcctg x + arcctg y = π/2,

61. arcsin x > arcsin(1 — x);

62. arcsin(1 – x) + 2arcsin x > π/2;

63. arctg(x –1) + arctg x + arctg(x +) > arctg3x;

64. sin((arccos x)/5)= 1;

65. arctg(x 2 – 3x – 3) = -3π/4;

66. arctg(x + x 2 ) + arctg(x 2 – x) = π/4;

67. arctg3 x – arctg3 -x = π/6;

68. arccos (3ax + 1)  arccos(2x + 3a – 1);

69. arcsin x = arcsin(a 2 + a – 1)(x – 2a 2 – 3a +2);

источники:

http://www.sites.google.com/site/trigonometriavneskoly/obratnye-trigonometriceskie-uravnenia-i-neravenstva

http://infourok.ru/uravneniya-i-neravenstva-soderzhashie-obratnye-trigonometricheskie-funkcii-4451977.html