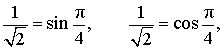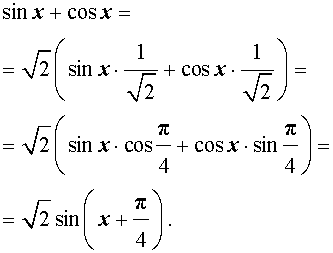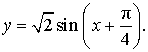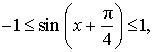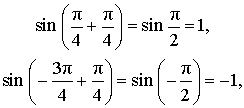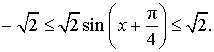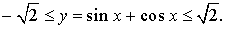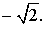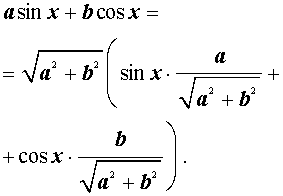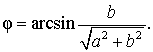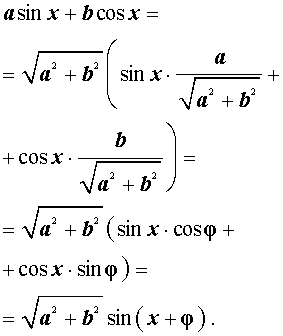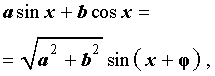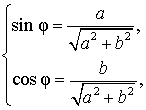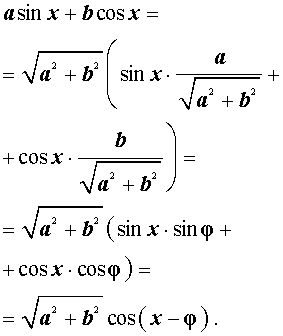Тригонометрические уравнения введение вспомогательного угла

Метод введения дополнительного угла (Метод введения вспомогательного аргумента)

Рассмотрим метод введения дополнительного угла на примере решения следующей задачи.

ЗАДАЧА . Найти наибольшее и наименьшее значения функции

РЕШЕНИЕ . Заметив, что

преобразуем правую часть формулы (1):

Отсюда вытекает, что выражение (1) можно переписать в виде:

ОТВЕТ . Наибольшее значение функции (1) равно , наименьшее значение функции (1) равно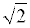

ЗАМЕЧАНИЕ . В рассмотренной задаче угол 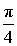и является дополнительным углом.

Теперь докажем формулу дополнительного угла (вспомогательного аргумента) в общем виде. Для этого рассмотрим выражение

где a и b – произвольные, отличные от нуля числа, и преобразуем его:

Введем дополнительный угол (вспомогательный аргумент) φ , у которого:

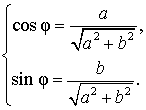(4)

В случае, когда a и b являются положительными числами, в качестве дополнительного угла можно взять, например, угол

Тогда выражение (3) принимает вид:

Таким образом, мы получили формулу

которую и называют формулой дополнительного угла (вспомогательного аргумента).

Если же дополнительный угол, в отличие от формул (4), ввести по формулам

то выражение (3) примет вид

и мы получаем другой вид формулы дополнительного угла:

Метод введения вспомогательного угла

Преобразование выражения a sin х + b cos х путем введения вспомогательного угла

Лемма . Если сумма квадратов двух действительных чисел равна единице, то одно из этих чисел можно рассматривать как косинус, а другое как синус некоторого угла.

Другими словами, если а 2 + b 2 = 1, то существует угол φ, такой, что

Прежде чем доказывать эту лемму, поясним ее на следующем примере:

Поэтому существует угол φ, такой, что \( \frac<\sqrt3> <2>\) = cos φ; 1 /₂ = sin φ.

В качестве φ в данном случае можно выбрать любой из углов 30°, 30° ± 360°, 30° ± 2 • 360° и т. д.

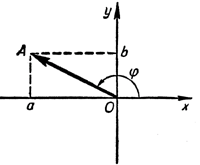
Рассмотрим вектор \(\vec<0А>\) с координатами (а, b). Поскольку а 2 + b 2 = 1, длина этого вектора равна 1. Но в таком случае его координаты должны быть равны cos φ и sin φ, где φ — угол, который образует данный вектор с осью абсцисс.

Итак, а = cos φ; b =sin φ, что и требовалось доказать.

Доказанная лемма позволяет преобразовать выражение a sin х + b cos х к более удобному для изучения виду.

Прежде всего вынесем за скобки выражение \(\sqrt\)

Но в таком случае

a sin х + b cos х = \(\sqrt\)(cos φ sin х + sin φ cos х) = \(\sqrt\) sin ( x + φ )

a sin х + b cos х = \(\sqrt\) sin (x + φ) , где угол φ определяется из условий

1) \( sin x + cos x = \sqrt2 (\frac<1> <\sqrt2>sin x + \frac<1><\sqrt2>cos x) = \sqrt2 (cos\frac<\pi><4>sin x + sin\frac<\pi><4>cos x ) =\\= \sqrt2(sinx + \frac<\pi><4>) \)

Полученную формулу sin x + cos x = \(\sqrt2(sinx + \frac<\pi><4>)\)полезно запомнить.

2) Если одно из чисел а и b положительно, а другое отрицательно, то выражение
a sin х + b cos х удобнее преобразовывать не к синусу суммы, а к синусу разности двух углов. Так,

$$ 3sinx — 4cosx = \sqrt<9+16>(\frac<3><\sqrt<9+16>>sinx — \frac<4><\sqrt<9+16>>cosx) =\\= 5(sinx\cdot\frac<3> <5>— cosx\cdot\frac<4><5>) = 5sin(x — \phi), $$

где под φ можно подразумевать любой угол, удовлетворяющий условиям:

В частности, можно положить φ = arctg 4 /₃. Тогда получим:

3 sin х — 4 cos x = 5 sin (x — arctg 4 /₃).

Тригонометрические уравнения введение вспомогательного угла

Тогда можно обозначить их соответственно $$ \cos \varphi \;и\;\sin \varphi $$ (здесь $$ \varphi $$- вспомогательный угол)
и наше уравнение принимает вид: $$ \cos \varphi \sin x + \sin \varphi \cos x = C$$,
где $$ \frac <<\sqrt >> = \cos \varphi ;\;\quad \frac <<\sqrt >> = \sin \varphi ;\quad \;\frac <<\sqrt >> = C$$.
Тогда $$ \sin (x + \varphi ) = C $$.

И его решение $$ x = ( — 1)^k \arcsin C — \varphi + \pi k,\;\quad k \in <\rm Z>$$,
где $$ \varphi = \arccos \frac <<\sqrt >> = \arcsin \frac <<\sqrt >> $$.

Заметим, что введенные обозначения $$ \cos \varphi \quad и\quad \sin \varphi $$ взаимно заменяемы.

Решить уравнение $$ \sqrt 3 \sin 3x — \cos 3x = 1 $$

Решение: Согласно теории $$ a = \sqrt 3 ;\;\quad b = — 1$$,
поэтому делим обе части уравнения на $$ \sqrt <3 + 1>= 2 $$.
$$ \frac<<\sqrt 3 >><2>\sin 3x — \frac<1><2>\cos 3x = \frac<1> <2>\Rightarrow \cos \frac<\pi ><6>\sin 3x — \sin \frac<\pi ><6>\cos 3x = \frac<1> <2>\Rightarrow \sin \left( <3x - \frac<\pi ><6>> \right) = \frac<1><2>$$.

Решая последнее уравнение получим ответ:
$$ — \frac<\pi > <6>+ 3x = ( — 1)^k \frac<\pi > <6>+ \pi k,\;\quad k \in <\rm Z>\Rightarrow x = ( — 1)^k \frac<\pi ><<18>> + \frac<\pi ><<18>> + \frac<<\pi k>><3>,\;\quad k \in <\rm Z>$$