Целое уравнение и его корни объяснение темы

Алгебра

План урока:

Целое уравнение и его степень

Ранее мы уже изучали понятие целого выражения. Так называют любое выражение с переменной, в котором могут использоваться любые арифметические операции, а также возведение в степень. Однако есть важное ограничение – в целом выражении переменная НЕ может находиться в знаменателе какой-нибудь дроби или быть частью делителя. Также переменная не может находиться под знаком корня. Для наглядности приведем примеры целых выражений:

(n 3 + 7)/5 (в знаменателе находится только число, без переменной);

А вот примеры нецелых выражений:

Отличительной особенностью целых выражений является то, что в них переменная может принимать любое значение. В нецелых же выражениях возникают ограничения на значения переменной, ведь знаменатель дроби не должен равняться нулю, в выражение под знаком корня не должно быть отрицательным.

Введем понятие целого уравнения.

Приведем примеры целых ур-ний:

0,75х 7 + 0,53х 6 – 45х = 18

Напомним, что в математике существует понятие равносильных уравнений.

Когда мы решаем ур-ния, мы в каждой новой строчке записываем ур-ние, равносильное предыдущему. Для этого используются равносильные преобразования (перенос слагаемых через знак «=» с противоположным знаком, деление обоих частей равенства на одинаковые числа и т. д.).

Можно доказать (мы этого делать не будем), что любое целое ур-ние можно возможно преобразовать так, чтобы получилось иное, равносильное ему ур-ние, где в левой части будет находиться многочлен, а справа – ноль. Для этого надо лишь раскрыть скобки и умножить ур-ние на какое-нибудь число, чтобы избавиться от дробей.

Пример. Преобразуйте целое ур-ние

так, чтобы слева стоял многочлен, а справа – ноль.

Решение. В ур-нии есть дроби со знаменателями 5 и 4. Если умножить обе части на 20 (это наименьшее общее кратное чисел 5 и 4), то дроби исчезнут:

Теперь раскроем скобки:

4(5х 3 – 3х 4 + 45х – 27х 2 ) – 40 = 10х 2 + 5х + 35

20х 3 – 12х 4 + 180х – 108х 2 – 40 = 10х 2 + 5х + 35

Осталось перенести все слагаемые влево и привести подобные слагаемые:

20х 3 – 12х 4 + 180х – 108х 2 – 40 – 10х 2 – 5х – 35 = 0

– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0

Получили ур-ние в той форме, которую и надо было найти по условию.

Ответ:– 12х 4 + 20х 3 – 118х 2 + 175х – 75 = 0

В математике любой полином можно обозначить как Р(х). Если ур-ние привели к тому виду, когда в одной части многочлен, а в другой ноль, то говорят, что получили ур-ние вида Р(х) = 0.

Получается, что решение целого уравнения всегда можно свести к решению равносильного ему ур-ния Р(х) = 0. Именно поэтому многочлены играют такую большую роль в математике

Напомним, что степенью многочлена называется максимальная степень входящего в его состав одночлена. Это же число является и степенью целого уравнения Р(х) = 0, а также степенью любого равносильного ему целого ур-ния.

Пример. Определите степень ур-ния

(х 3 – 5)(2х + 7) = 2х 4 + 9

Решение. Приведем ур-ние к виду Р(х) = 0. Для этого раскроем скобки:

(х 3 – 5)(2х + 7) = 2х 4 + 9

2х 4 + 7х 3 – 10х – 35 = 2х 4 + 9

Перенесем все слагаемые влево и приведем подобные слагаемые:

2х 4 + 7х 3 – 10х – 35 – 2х 4 – 9 = 0

7х 3 – 10х – 44 = 0

Получили в левой части многочлен 3-ей степени. Следовательно, и исходное ур-ние имело такую же степень

Приведем примеры ур-ний первой степени:

5,4568у + 0,0002145 = 0

Все они являются линейными ур-ниями, метод их решения изучался ранее. Они имеют 1 корень.

Приведем примеры ур-ний второй степени:

6t 2 + 98t – 52 = 0

Это квадратные ур-ния. У них не более двух действительных корней. Для их нахождения в общем случае надо вычислить дискриминант и использовать формулу

Квадратные и линейные ур-ния умели решать ещё в Древнем Вавилоне 4 тысячи лет назад! А вот с ур-ния 3-ей степени (их ещё называют кубическими уравнениями) оказались значительно сложнее. Приведем их примеры:

2х 3 + 4х 2 – 19х + 17 = 0

Лишь в 1545 году итальянец Джералимо Кардано опубликовал книгу, в которой описывался общий алгоритм решения кубических ур-ний. Он достаточно сложный и не входит в школьный курс математики. Его ученик, Лодовико Феррари, предложил метод решения ур-ний четвертой степени. В качестве примера такого ур-ния можно привести:

5х 4 + 6х 3 – 2х 2 – 10х + 1 = 0

Лишь в XIX веке было доказано, что для ур-ний более высоких степеней (5-ой, 6-ой и т. д.) не существует универсальных формул, с помощью которых можно было бы найти их корни.

Отметим, что если степень целого ур-ния равна n, то у него не более n корней (но их число может быть и меньше). Так, количество корней кубического уравнения не превышает трех, а у ур-ния 4-ой степени их не более 4.

Чтобы доказать это утверждение, сначала покажем способ составления уравнения Р(х) = 0, имеющего заранее заданные корни. Пусть требуется составить ур-ние, имеющее корни k₁, k₂,k₃,…k_n. Приравняем к нулю следующее произведение скобок:

Составленное ур-ние имеет все требуемые корни и никаких других корней. Действительно, произведение множителей может равняться нулю только в случае, если хотя бы один из множителей нулевой. Поэтому для решения ур-ния

надо каждую скобку приравнять к нулю:

х – k₁ = 0 или х – k₂ = 0 или х – k₃ = 0 или…х – k_n = 0

Перенесем второе слагаемое вправо в каждом равенстве и получим:

Чтобы вместо произведения скобок слева стоял многочлен, надо просто раскрыть скобки.

Пример. Составьте уравнение в виде Р(х) = 0, имеющее корни 1, 2, 3 и 4.

Запишем целое ур-ние, имеющее требуемые корни:

(х – 1)(х – 2)(х – 3)(х – 4) = 0

Будем поочередно раскрывать скобки, умножая 1-ую скобку на 2-ую, полученный результат на 3-ю и т.д.:

(х 2 – 3х + 2)(х – 3)(х – 4) = 0

(х 3 – 6х 2 + 11х – 6)(х – 4) = 0

х 4 – 10х 3 + 35х 2 – 50х +24 = 0

Получили ур-ние вида Р(х) = 0. Для проверки вычислений можно подставить в него числа 1, 2, 3 и 4 и убедиться, что они обращают ур-ние в верное равенство.

Ответ: х 4 – 10х 3 + 35х 2 – 50х +24 = 0

Заметим, что в рассмотренном примере, когда мы перемножали многочлены, мы получали новый полином, чья степень увеличивалась на единицу. Мы перемножили 4 скобки (х – k₁), а потому получили полином 4 степени. Если бы мы перемножали, скажем, 10 таких скобок, то и многочлен бы получился 10-ой степени. Именно поэтому ур-ние n-ой степени не более n корней.

Действительно, предположим, что какое-то ур-ние n-ой степени имеет хотя бы (n + 1) корень. Обозначим эти корни как k₁, k₂,k₃,…k_n, k_n+1 и запишем уравнение:

Оно, по определению, равносильно исходному ур-нию, ведь оно имеет тот же набор корней. Слева записаны (n + 1) скобок, поэтому при их раскрытии мы получим полином степени (n + 1). Значит, и исходное ур-ние на самом деле имеет степень n + 1, а не n. Получили противоречие, которое означает, что на самом деле у уравнения n-ой степени не более n корней.

Особо акцентируем внимание на том факте, что если корнями уравнения являются некоторые числа k₁, k₂,k₃,…k_n, то этому ур-нию равносильна запись (х – k₁)(х – k₂)(х – k₃)…(х – k_n) = 0

Этот факт будет использован далее при решении ур-ний.

Решение уравнений методом подбора корня

Необязательно преобразовывать ур-ние, чтобы найти его корни. Одним из приемов решения целых уравнений является метод подбора корня. Ведь если надо доказать, что какое-то число – это корень ур-ния, достаточно просто подставить это число в ур-ние и получить справедливое равенство!

Пример. Докажите, что корнями ур-ния

х 3 – 2х 2 – х + 2 = 0

являются только числа (– 1), 1 и 2.

Решение. Подставим в ур-ние каждую из предполагаемых корней и получим справедливое равенство. При х = – 1 имеем:

(– 1) 3 – 2(– 1) 2 – (– 1) + 2 = 0

При х = 1 получаем:

1 3 – 2•1 2 – 1 + 2 = 0

Наконец, рассмотрим случай, когда х = 2

2 3 – 2•2 2 – 2 + 2 = 0

Исходное ур-ние имеет 3-ю степень, поэтому у него не более 3 корней. То есть других корней, кроме (– 1), 1 и 2 , у него нет.

Конечно, просто так подобрать корни довольно тяжело. Однако есть некоторые правила, которые помогают в этом. Для начала введем понятие коэффициентов уравнения.

Понятно, что ур-ние Р(х) = 0 в общем виде можно записать так:

Числа а₀, а₁, а₂,…а_nи называют коэффициентами уравнений.

Например, для уравнения

5х 4 – 7х 3 + 9х 2 – х + 12 = 0

Если одна из слагаемых «пропущено» в уравнении, то считают, что коэффициент перед ним равен нулю. Например, в ур-нии

нет слагаемого с буквенной частью х 2 . Можно считать, что ур-ние равносильно записи

х 3 + 0х 2 + 2х – 15 = 0

где слагаемое х 2 есть, но перед ним стоит ноль. Тогда коэффициент а₁ = 0.

Для обозначения первого коэффициента а₀ может использоваться термин старший коэффициент, а для последнего коэффициента а_n – термин «свободный член» или «свободный коэффициент».

Изучение коэффициентов ур-ния помогает быстрее подобрать корень. Существует следующая теорема:

Докажем это утверждение. Пусть m – это целый корень уравнения с целыми коэффициентами

Тогда можно подставить туда число m и получить верное равенство:

Поделим обе его части на m и получим

Справа – целое число (ноль), значит, и сумма чисел слева также целая. Все числа а₀m n –1 , a₁m n –2 , а_n–1, очевидно, целые (так как и целыми являются и m, и все коэффициенты). Значит, и число а_n/m должно быть целым. Но это возможно лишь в том случае, если m является делителем числа а_n.

Из доказанной теоремы следует, что при подборе корней ур-ния достаточно рассматривать только те из них, которые являются делителями свободного члена. При этом следует учитывать и отрицательные делители.

Пример. Найдите целые корни уравнения

2х 4 – х 3 – 9х 2 + 4х + 4 = 0

Решение. Все коэффициенты ур-ния – целые, а потому целый корень должен быть делителем свободного члена, то есть числа 4. Делителями четверки являются 1 и (– 1), 2 и (– 2), 4 и (– 4). Подставляя каждое из этих чисел в ур-ние, получим верные равенства только для чисел 1, 2 и (– 2):

2•1 4 – 1 3 – 9•1 2 + 4•1 + 4 = 2 – 1 – 9 + 4 + 4 = 0

2•2 4 – 2 3 – 9•2 2 + 4•2 + 4 = 32 – 8 – 36 + 8 + 4 = 0

2•(– 2) 4 – (– 2) 3 – 9•(– 2) 2 + 4(– 2) + 4 = 32 + 8 – 36 – 8 + 4 = 0

Таким образом, только эти числа и могут быть целыми корнями ур-ния. Так как мы рассматриваем ур-ние 4 степени, то, возможно, у него помимо 3 целых корней есть ещё один дробный.

Пример. Решите ур-ние

0,5х 3 + 0,5х + 5 = 0

Решение. У ур-ния дробные коэффициенты. Умножим обе части равенства на 2 и получим ур-ние с целыми коэффициентами:

0,5х 3 + 0,5х + 5 = 0

(0,5х 3 + 0,5х + 5)•2 = 0•2

Попытаемся подобрать целый корень ур-ния. Он должен быть делителем свободного члена, то есть десятки. Возможными кандидатами являются числа 1 и (– 1), 2 и (– 2), 5 и (– 5), 10 и (– 10). Подходит только корень х = – 2:

(– 2) 3 + (– 2) + 10 = – 8 – 2 + 10 = 0

Обратим внимание, что в левой части ур-ния стоит сумма функций, возрастающих на всей числовой прямой: у = х 3 и у = х + 10. Значит, и вся левая часть х 3 + х + 10 монотонно возрастает. Это значит, что у ур-ния есть только один корень, и мы его нашли ранее подбором.

Ещё быстрее можно узнать, является ли единица корнем уравнения.

Докажем это. Подставим в ур-ние

значение х = 1. Так как единица в любой степени равна самой единице, то получим:

Получили равенство, в котором слева стоит сумма коэффициентов, в справа – ноль. Если сумма коэффициентов действительно равна нулю, то равенство верное, а, значит, единица является корнем ур-ния.

Пример. Укажите хотя бы 1 корень ур-ния

499х 10 – 9990х 7 + 501х 6 – 10х 5 + 10000х 4 – 1000 = 0

Решение. Заметим, что при сложении коэффициентов ур-ния получается 0:

499 – 9990 + 501 – 10 + 10000 – 1000 = (499 + 501 – 1000) + (10000 – 9990 – 10) = 0 + 0 = 0

Следовательно, единица является его корнем.

Решение уравнений с помощью разложения многочлена на множители

Если в уравнении вида P(x) = 0в левой части удается выполнить разложение многочлена на множители, то дальше каждый из множителей можно отдельно приравнять к нулю.

Пример. Решите ур-ние

Решение. Степень х 4 можно представить как (х 2 ) 2 , а 16 – как 4 2 . Получается, что слева стоит разность квадратов, которую можно разложить на множители по известной формуле:

(х 2 – 4)(х 2 + 4) = 0

Приравняем каждую скобку к нулю и получим два квадратных ур-ния:

х 2 – 4 = 0 или х 2 + 4 = 0

х 2 = 4 или х 2 = – 4

Первое ур-ние имеет два противоположных корня: 2 и (– 2). Второе ур-ние корней не имеет.

Предположим, что у ур-ния 3-ей степени есть 3 корня, и подбором мы нашли один из них. Как найти оставшиеся корни? Здесь помогает процедура, известная как «деление многочленов в столбик». Продемонстрируем ее на примере. Пусть надо решить ур-ние

100х 3 – 210х 2 + 134х – 24 = 0

Можно заметить, сумма всех коэффициентов ур-ния равна нулю:

100 – 210 + 134 – 24 = 0

Следовательно, первый корень – это 1.

Предположим, что у исходного ур-нияР(х) = 0 есть 3 корня, k₁, k₂и k₃. Тогда ему равносильно другое ур-ние

Мы нашли, что первый корень k₁ = 1, то есть

Обозначим как P₁(x) = 0 ещё одно ур-ние, корнями которого будут только числа k₂ и k₃. Очевидно, что корнями ур-ния

Будут числа 1, k₂ и k₃. Его корни совпадают с корнями исходного ур-ния, а потому запишем

(х – 1)•P₁(x) = 100х 3 – 210х 2 + 134х – 24

Поделим обе части на (х – 1):

Итак, если «поделить» исходное ур-ние на х – 1, то получим какой-то многочлен Р₁(х), причем решением уравнения P₁(x) = 0 будут оставшиеся два корня, k₂и k₃. Деление можно выполнить в столбик. Для этого сначала запишем «делимое» и «делитель», как и при делении чисел:

Смотрим на первое слагаемое делимого. Это 100х 3 . На какой одночлен нужно умножить делитель (х – 1), чтобы получился полином со слагаемым 100х 3 ? Это 100х 2 . Действительно, (х – 1)100х 2 = 100х 3 – 100х 2 . Запишем слагаемое 100х 2 в результат деления, а результат его умножения на делитель, то есть 100х 3 – 100х 2 , вычтем из делимого:

Теперь вычтем из делимого то выражение, которое мы записали под ним. Слагаемые 100х 3 , естественно, сократятся:

(100х 3 – 210х 2 ) – (100х 3 – 100х 2 ) = 100х 3 – 210х 2 – 100х 3 + 100х 2 = – 110х 2

Далее снесем слагаемое 134х вниз:

На какое слагаемое нужно умножить (х – 1), что получился полином со слагаемым (– 110х 2 ). Очевидно, на (– 110х):

(х – 1)(– 110х 2 ) = –110х 2 + 110х

Запишем в поле «ответа» слагаемое (– 110х 2 ), а под делимый многочлен – результат его умножения на (х – 1):

При вычитании из (–110х 2 + 134х) полинома (–110х 2 + 110х) остается 24х. Далее сносим последнее слагаемое делимого многочлена вниз:

Выражение х – 1 нужно умножить на 24, чтобы получить 24х – 24. Запишем в поле «ответа» число 24, а в столбике произведение 24(х –1) = 24х – 24:

В результате в остатке получился ноль. Значит, всё сделано правильно. С помощью деления столбиком мы смогли разложить полином 100х 3 – 210х 2 + 134х – 24 на множители:

100х 3 – 210х 2 + 134х – 24 = (х – 1)(100х 2 – 110х + 24)

Теперь перепишем исходное ур-ние с учетом этого разложения:

100х 3 – 210х 2 + 134х – 24 = 0

(х – 1)(100х 2 – 110х + 24) = 0

Теперь каждую отдельную скобку можно приравнять нулю. Получим ур-ние х – 1 = 0, корень которого, равный единице, мы уже нашли подбором. Приравняв к нулю вторую скобку, получим квадратное ур-ние:

100х 2 – 110х + 24 = 0

D =b 2 – 4ас = (– 110) 2 – 4•100•24 = 12100 – 9600 = 2500

Итак, мы нашли три корня ур-ния: 1; 0,3 и 0,8.

В данном случае мы воспользовались следующим правилом:

Пример. Решите уравнение

2х 3 – 8х 2 + 16 = 0

Решение. Все коэффициенты целые, а потому, если у уравнения есть целый корень, то он должен быть делителем 16. Перечислим эти делители: 1, – 1, 2, – 2, 4, – 4, 8, – 8, 16, – 16. Из всех них подходит только двойка:

2•2 3 – 8•2 2 + 16 = 16 – 32 + 16 = 0

Итак, первый корень равен 2. Это значит, что исходный многочлен можно разложить на множители, один из которых – это (х – 2). Второй множитель найдем делением в столбик. Так как в многочлене 2х 3 – 8х 2 + 16 нет слагаемого с буквенной часть х, то искусственно добавим её:

2х 3 – 8х 2 + 16 = 2х 3 – 8х 2 + 0х + 16

Теперь возможно деление:

Получили, что 2х 3 – 8х 2 + 16 = (х – 2)(2х – 4х – 8)

С учетом этого перепишем исходное ур-ние:

2х 3 – 8х 2 + 16 = 0

(х – 2)(2х – 4х – 8) = 0

х – 2 = 0 или 2х – 4х – 8 = 0

Решим квадратное ур-ние

D =b 2 – 4ас = (– 4) 2 – 4•2•(– 8) = 16 + 64 = 80

В 8 классе мы узнали, что если у квадратного ур-ния ах 2 + bx + c = 0 есть два корня, то многочлен ах 2 + bx + c можно разложить на множители по формуле

где k₁ и k₂– корни квадратного ур-ния. Оказывается, такое же действие можно выполнять с многочленами и более высоких степеней. В частности, если у кубического ур-ния есть 3 корня k₁, k₂ и k₃, то его можно разложить на множители по формуле

Пример. Разложите на множители многочлен 2х 3 – 4х 2 – 2х + 4.

Решение. Целые корни этого многочлена (если они есть), должны быть делителем четверки. Из всех таких делителей подходят три: 1, (– 1) и 2:

2•1 3 – 4•1 2 – 2•1 + 4 = 2 – 4 – 2 + 4 = 0

2•(– 1) 3 – 4•(– 1) 2 – 2•(– 1) + 4 = – 2 – 4 + 2 + 4 = 0

2•2 3 – 4•2 2 – 2•2 + 4 = 16 – 16 – 4 + 4 = 0

Значит, многочлен можно разложить на множители:

2х 3 – 4х 2 – 2х + 4 = 2(х + 1)(х – 1)(х – 2)

Возникает вопрос – почему перед скобками нужна двойка? Попробуем сначала перемножить скобки без ее использования:

(х + 1)(х – 1)(х – 2) = (х 2 – 1)(х – 2) = х 3 – 2х 2 – х + 2

Получили не тот многочлен, который стоит в условии. Однако ур-ние

х 3 – 2х 2 – х + 2 = 0

имеет те же корни (1, 2 и (– 1)), что и ур-ние

2х 3 – 4х 2 – 2х + 4 = 0

Дело в том, что это равносильные ур-ния, причем второе получено умножением первого на два:

2•(х 3 – 2х 2 – х + 2) = 2х 3 – 4х 2 – 2х + 4

Надо понимать, что хотя ур-ния 2х 3 – 4х 2 – 2х + 4 = 0 и х 3 – 2х 2 – х + 2 = 0, по сути, одинаковы, многочлены в их левой части различны. Заметим, что при перемножении скобок (х – k₁), (х – k₂), (х – k₃) и т.д. всегда будет получаться полином, у которого старший коэффициент равен единице. Поэтому, чтобы учесть этот самый коэффициент, надо домножить произведение скобок на него:

2х 3 – 4х 2 – 2х + 4= 2•(х 3 – 2х 2 – х + 2) = 2(х + 1)(х – 1)(х – 2)

Ответ: 2(х + 1)(х – 1)(х – 2).

Графический метод решения уравнений

Любое ур-ние с одной переменной можно представить в виде равенства

где у(х) и g(x) – некоторые функции от аргумента х.

Построив графики этих функций, можно примерно найти точки их пересечений. Они и будут соответствовать корням уравнения.

Пример. Решите графически уравнение

Решение. Строить график уравнения х 3 – х 2 – 1 = 0 довольно сложно, поэтому перенесем слагаемое (– х 2 – 1) вправо:

Построим графики у = х 3 и у = х 2 + 1 (второй можно получить переносом параболы у = х 2 на единицу вверх):

Видно, они пересекаются в точке, примерно соответствующей значению х ≈ 1,4. Если построить графики уравнения более точно (с помощью компьютера), то можно найти, что х ≈ 1,46557.

Ответ: х ≈ 1,46557

Конечно, графический метод решения уравнений не является абсолютно точным, однако он помогает быстро найти примерное положение корня. Также с его помощью можно определить количество корней уравнения. В рассмотренном примере был только 1 корень.

Пример. Определите количество корней уравнений

б) х 3 – 2х + 0,5 = 0

Решение. Перенесем два последних слагаемых вправо в каждом ур-нии:

Построим графики функций у = х 3 , у = х + 3 и у = 2х – 0,5:

Видно, что прямая у = х + 3 пересекает график у = х 3 в одной точке, поэтому у первого ур-ния будет 1 решение.Прямая у = 2х – 0,5 пересекает кубическую параболу в трех точках, а потому у второго ур-ния 3 корня.

Ответ: а) один корень; б) три корня.

Решение дробно-рациональных уравнений

До этого мы рассматривали только целые ур-ния, где переменная НЕ находится в знаменателе какого-нибудь выражения. Однако, если в ур-нии есть выр-ние, содержащее переменную в знаменателе, или присутствует деление на выр-ние с переменной, то его называют дробно-рациональным уравнением.

Приведем несколько примеров ур-ний, считающихся дробно-рациональными:

С помощью равносильных преобразований любое дробно-рациональное ур-ние возможно записать в виде отношения двух полиномов:

Дробь равна нулю лишь тогда, когда ее числитель равен нулю, а знаменатель – не равен. Таким образом, нужно сначала решить ур-ние Р(х) = 0 и потом проверить, что полученные корни не обращают полином Q(x) в ноль.

Обычно для решения дробно-рациональных уравнений используют такой алгоритм:

1) Приводят все дроби к единому знаменателю, умножают на него ур-ние и получают целое ур-ние.

2) Решают полученное целое ур-ние.

3) Исключают из числа корней те, которые обращают знаменатель хотя бы одной из дробей в ноль.

Пример. Решите ур-ние

Умножим обе части равенства на знаменатель 1-ой дроби:

2х 2 – 3х – 2 = х 2 (х – 2)

Раскроем скобки и перенесем все слагаемые в одну сторону:

2х 2 – 3х – 2 = х 3 – 2х 2

х 3 – 2х 2 – 2х 2 + 3х + 2 = 0

х 3 – 4х 2 + 3х + 2 = 0

У ур-ния могут быть только те целые корни, которые являются делителями двойки. Из кандидатов 1, – 1, 2 и – 2 подходит только двойка:

2 3 – 4•2 2 + 3•2 + 2 = 8 – 16 + 6 + 2 = 0

Нашли один корень, а потому исходный многочлен можно поделить в столбик на (х – 2):

Получили, что х 3 – 4х 2 + 3х + 2 = (х – 2)(х 2 – 2х – 1)

Тогда ур-ние примет вид:

(х – 2)(х 2 – 2х – 1) = 0

х – 2 = 0 или х 2 – 2х – 1 = 0

Решим квадратное ур-ние:

D =b 2 – 4ас = (– 2) 2 – 4•1•(– 1) = 4 + 4 = 8

Мы нашли все 3 корня кубического ур-ния. Теперь надо проверить, не обращают ли какие-нибудь из них знаменатели дроби в исходном ур-нии

в ноль. Очевидно, что при х = 2 знаменатель (х – 2) превратится в ноль:

Это значит, что этот корень надо исключить из списка решений. Такой корень называют посторонним корнем ур-ния.

Также ясно, что два остальных корня не обращают знаменатель в ноль, а потому они НЕ должны быть исключены из ответа:

Пример. Найдите все корни ур-ния

Решение. Если сразу привести выражение слева к общему знаменателю 4(х 2 + х – 2)(х 2 + х – 20), то получится очень длинное и неудобное выражение. Однако знаменатели довольно схожи, поэтому можно провести замену. Обозначим х 2 + х как у:

Тогда уравнение примет вид

Приведем дроби к общему знаменателю 4(у – 2)(у – 20):

Знаменатель должен равняться нулю:

4(у – 20) + 28(у – 2) + (у – 2)(у – 20) = 0

4у – 80 + 28у – 56 + у 2 – 20у – 2у + 40 = 0

у 2 + 10у – 96 = 0

Решаем квадратное ур-ние:

D =b 2 – 4ас = (10) 2 – 4•1•(– 96) = 100 + 384 = 484

Получили, что у₁ = – 16, а у₂ = 6. Произведем обратную замену:

х 2 + х = – 16 или х 2 + х = 6

х 2 + х + 16 = 0 или х 2 + х – 6 = 0

Дискриминант 1-ого ур-ния отрицателен:

D =b 2 – 4ас = (1) 2 – 4•1•(16) = 1– 64 = – 63

А потому оно не имеет решений. Решим 2-ое ур-ние:

D = b 2 – 4ас = (1) 2 – 4•1•(– 6) = 1+ 24 = 25

Нашли два корня: 2 и (– 3). Осталось проверить, не обращают ли они знаменатели дробей в ур-нии

в ноль. Подстановкой можно убедиться, что не обращают.

При решении дробно-рациональных ур-ний может использоваться и графический метод.

Пример. Сколько корней имеет уравнение

Решение. Построим графики функций у = х 2 – 4 и у = 2/х:

Видно, что графики пересекаются в 3 точках, поэтому ур-ние имеет 3 корня.

Конспекты уроков по алгебре в 9 классе по теме «Целое уравнение и его корни»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выберите документ из архива для просмотра:

Выбранный для просмотра документ УРОК1,2 на конкурс.docx

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №14

села Орловки Буденновского района»

Конспекты уроков по алгебре в 9 классе

по теме «Целое уравнение и его корни»

2012-2013 уч. год

Тема урока: «Целое уравнение и его корни».

обобщить и углубить сведения об уравнениях;

ввести понятие целого уравнения и его степени, его корней;

рассмотреть способ решения целого уравнения с помощью разложения на множители;

развитие математического и общего кругозора, логического мышления, умение анализировать, делать вывод;

воспитывать самостоятельность, четкость и аккуратность в действиях.

Учебник: Алгебра. 9 класс: учебник для общеобразовательных учреждений/ [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А. Теляковского.- 16-е изд. – М.: Просвещение, 2010

Оборудование: компьютер с проектором, презентация «Целые уравнения»

Сообщение темы урока, цели.

Сегодня мы познакомимся с новым видом уравнений – это целые уравнения. Научимся их решать.

Запишем в тетради число, классная работа и тему урока: «Целое уравнение, его корни».

2.Актуализация опорных знаний.

Ответы: 1)х = -2; 2) х =1/2; 3) х = -4, +4; 4) х = -8; 5) корней нет; 6) х = 0

— определите степень каждого многочлена:

38х 5 +8-3 y 7 y -76х 6 9х-76х 2 +12

3.Формирование новых понятий.

Беседа с учениками:

Что такое уравнение? (равенство, содержащее неизвестное число)

Какие виды уравнений вы знаете? (линейные, квадратные)

Приведите примеры линейных уравнений, квадратных.

-Сколько корней может иметь линейное уравнение?) (один, множество и ни одного корня)

1)5х=0 2) 0 y =3 в)6х-2=4

-Какое из этих уравнений имеет один корень? (не имеет корней, имеет множество решений)

-Сколько корней может иметь квадратное уравнение?

Отчего зависит количество корней? (от дискриминанта)

-В каком случае квадратное уравнение имеет 2 корня?( Д>0)

— В каком случае квадратное уравнение имеет 1 корень? (Д=0)

— В каком случае квадратное уравнение не имеет корней? ( Д 0)

-Дадим определение данному типу уравнений, но для начала вспомним, какие выражения называются целыми? (Целые выражения это такие, которые состоят из умножения, сложения, вычитания выражений содержащих переменную, а также деления на число)

Целое уравнение – это уравнение левая и правая часть, которого является целым выражением. (читают вслух).

Приведем примеры целых уравнений:

Приведите и запишите свой пример целого уравнения (попросить нескольких учеников записать на доске свои уравнения)

-Из рассмотренных линейных и квадратных уравнений, мы видим, что количество корней не больше его степени.

-Как вы думаете, можно ли не решая уравнения, определить количество его корней? (возможные ответы детей)

-Познакомимся с правилом определения степени целого уравнения?

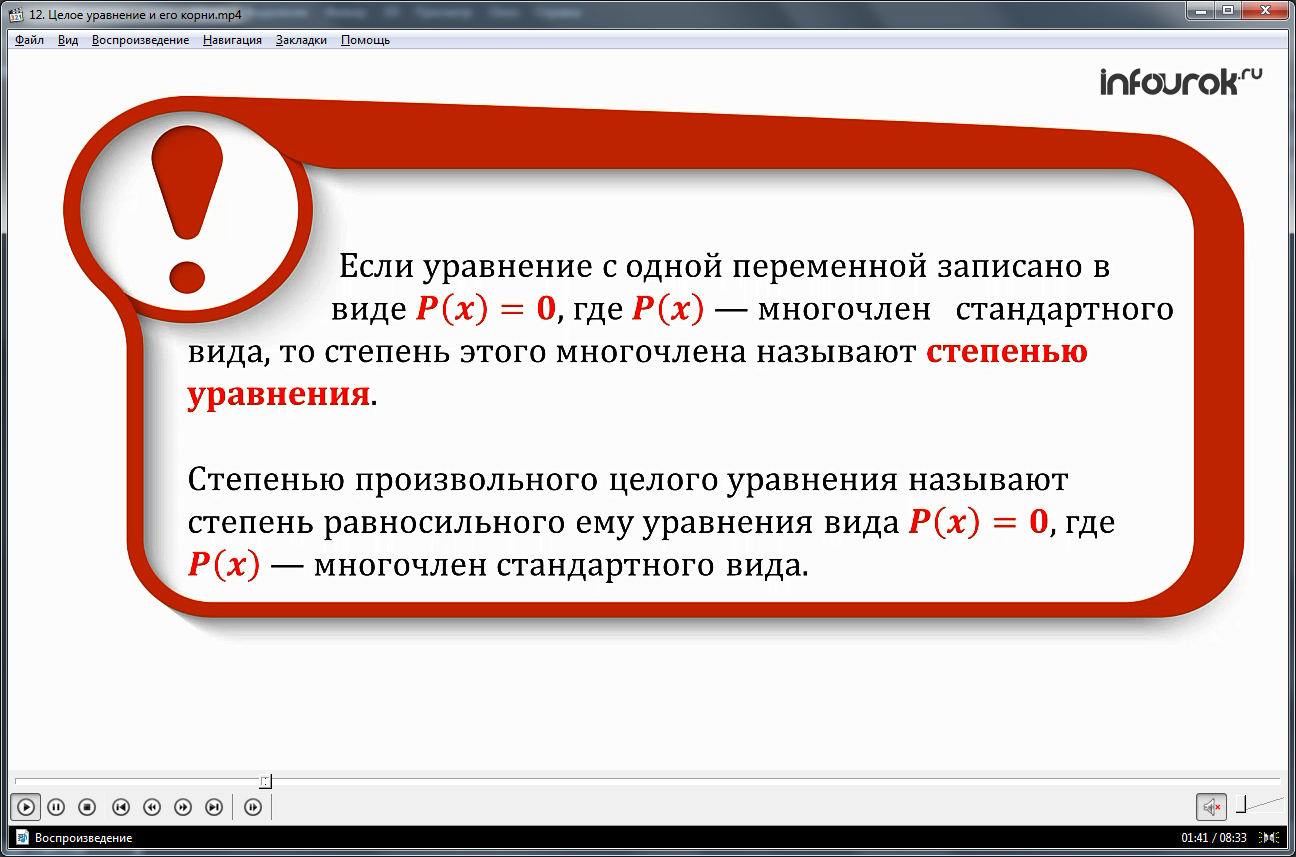
Если уравнение с одной переменной записано в виде Р(х)=0, где Р(х)- многочлен стандартного вида, то степень этого многочлена называют степенью уравнения. Степенью произвольного целого уравнения называют степень равносильного ему уравнения вида Р(х)=0, где Р(х)- многочлен стандартного вида.

Уравнение n ой степени имеет не более n корней.

Например: 1)4х 4 -5х 2 +1=0; 2)(х-2)(х+2)=0

-Являются ли эти уравнения целыми?

-Записаны ли эти уравнения в виде Р(х)=0?

-Степень какого уравнения можно определить сразу? (1)

-Сколько корней может иметь это уравнение?

-Что нужно сделать со вторым уравнением, чтобы определить его степень?

( заменить ему равносильным и записать в виде Р(х)=0)

— Замените это уравнение ему равносильным и запишите в виде Р(х)=0

-Определите степень полученного уравнения

— Сколько корней может иметь 2 уравнение?

Целое уравнение можно решить несколькими способами:

способы решения целых уравнений

разложение на множители графический введение новой

(Записывают схему в тетрадь)

Сегодня мы рассмотрим один из них: разложение на множители на примере следующего уравнения: ( на доске объясняет учитель , ученики записывают в тетрадь решение уравнения)

-Как называется способ разложения на множители, с помощью которого можно левую часть уравнения разложить на множители? (способ группировки). Разложим левую часть уравнения на множители, а для этого сгруппируем слагаемые, стоящие в левой части уравнения.

-Когда произведение множителей равно нулю? (когда хотя бы один из множителей равен нулю). Приравняем к нулю каждый множитель уравнения.

Решим полученные уравнения

-Сколько корней мы получили? (запись в тетради)

4.Формирование умений и навыков. Практическая часть.

работа по учебнику №265( устно а-в, г-д- запись в тетради)

Какова степень уравнения и сколько корней имеет каждое из уравнений:

Ответы: а) 5, б) 6, в) 5, г) 2, д) 1, е) 1

№ 266 (решение у доски с объяснением)

№ 268 (решение у доски с объяснением)

Докажите, что уравнение не имеет корней:

Запишем уравнение в виде 5 x 6 +6 x 4 + x 2 =–4.

В левую часть уравнения х входит только в четной степени, следовательно, число неотрицательное, а в правой части — число отрицательное, значит, уравнение корней не имеет.

Закрепление теоретического материала:

Какое уравнение с одной переменной называется целым? Приведите пример.

Как найти степень целого уравнения? Сколько корней имеет уравнение с одной переменной первой, второй степени?

— Дайте оценку своей работе и прикрепите цветной магнит на доске.

1)Отлично, вопросов нет …

2)Хорошо, но могу лучше …

Пока испытываю трудности …

7. Домашнее задание:

Тема урока: «Целое уравнение и его корни».

дать понятие биквадратного уравнения и способа его решения;

развивать умение определять степень целого уравнения, его корни;

рассмотреть способ решения целого уравнения третьей степени с помощью введения новой переменной;

развивать умение самостоятельно выбирать рациональный способ решения целого уравнения;

развитие математического и общего кругозора, логического мышления; умения ставить перед собой цель и делать выводы, выполнять безошибочно необходимые арифметические вычисления; развивать внимательность, собранность и аккуратность.

воспитывать самостоятельность, четкость и аккуратность в действиях.

развитие способности проявлять себя в различных социальных ролях- исполнителя, эксперта, исследователя, помощника; обучение культуре общения в коллективе .

Учебник: Алгебра. 9 класс: учебник для общеобразовательных учреждений/ [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А. Теляковского.- 16-е изд. – М.: Просвещение, 2010

Оборудование: компьютер с проектором, презентация «Целые уравнения»

Сообщение темы урока, цели.

-Сегодня на уроке мы продолжим работу по теме» Целое уравнение и его корни», познакомимся с новым способом решения целых уравнений. В тетрадях записываем число, классная работа, тему урока

2.Актуализация опорных знаний.

-Какое уравнение называется целым?

-Являются ли эти уравнения целыми? Почему? (т.к их левые и правые части являются целыми выражениями, то эти уравнения-целые)

-Найдите корни данных уравнений и определите их степень.

(х-5)(х+1)(3х-6) =0 ( корни :-1;2;5; 3степень)

х(х 2 -4)=0 (корни:-2;0;2; 3 степень)

(х 2 +49)(х+3)=0 (корень -3; 3 степень)

(2х-4)(х 3 -1)=0 (корни:1;2; 4 степень)

(х 3 +1)(х 2 -25)=0 (корни:-5;-1;5; 5 степень)

-Какими способами можно решать целые уравнения?

-В чём заключается сущность способа разложения на множители?

-Как вы думаете, всегда ли возможно решить целое уравнение этим способом?

3 . Изучение нового материала

1)решим уравнение (х 2 -5х+4)(х 2 -5х+6)=120 (1)

-Как будем решать это уравнение?

(раскроем скобки, перенесём все члены уравнения в левую часть, приведём подобные)

запись в тетрадях и на доске х 4 -10х 3 +6х 2- 5х 3 +25х 2 -30х+4х 2 -20х+24-120=0

х 4 -10х 3 +35х 2 -50х-96=0

-Знаем ли мы способ решения уравнения четвёртой степени? (ответы детей)

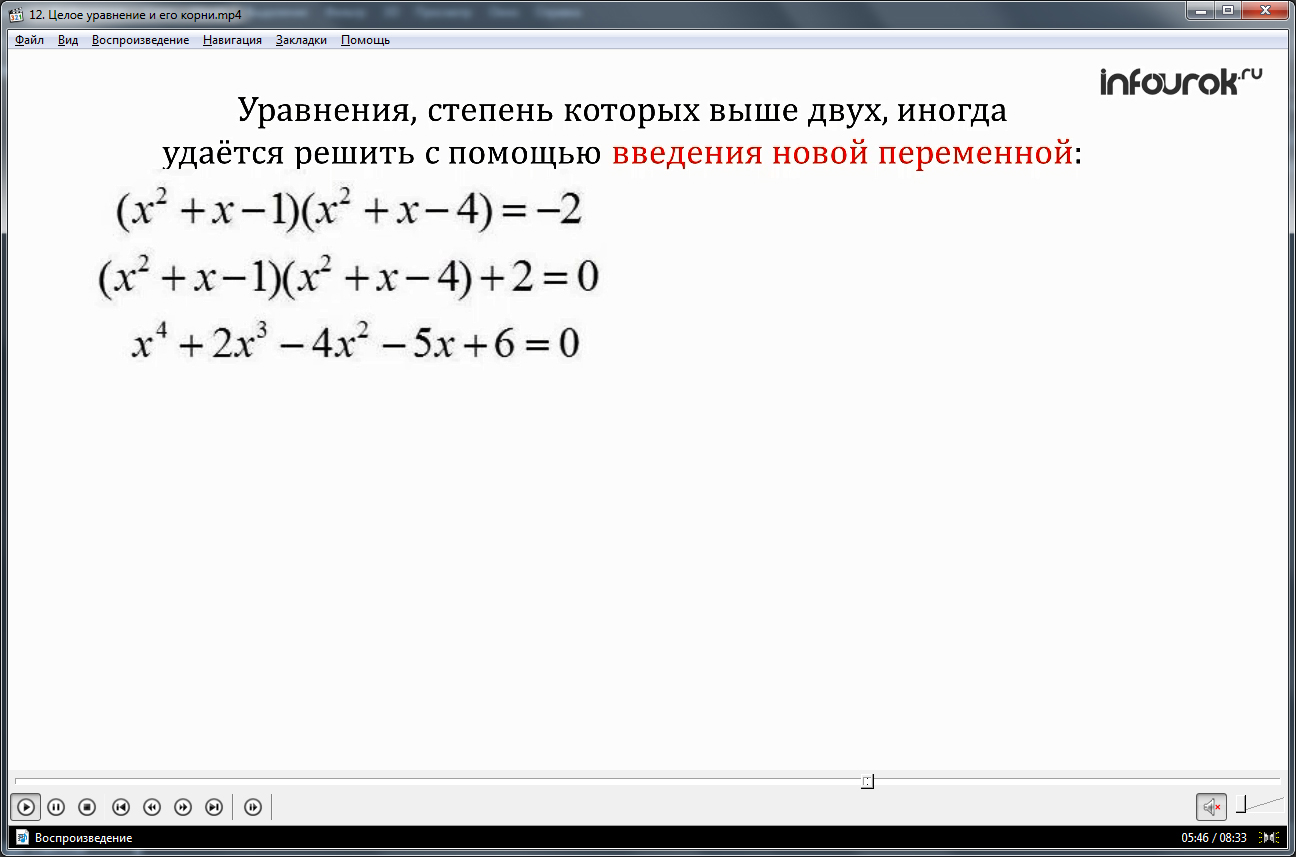
— Уравнения, степень которых выше двух, иногда удаётся решить, введя новую переменную

-Что особенного в уравнении (1)?

-В левой части уравнения (1) переменная х входит только в выражение х 2 -5х.

-Сколько раз повторяется это выражение? (дважды)

Это позволяет решить это уравнение с помощью введения новой переменной

(учитель объясняет и записывает решение на доске, а дети в тетради)

(х 2 -5х+4)(х 2 -5х+6)=120

1.Введём новую переменную y =х 2 -5х.

2.Получим уравнение (у+4)(у+6)=120.

3.Решим данное уравнение: у 2 +6у+4у+24-120=0

Д=10 2 -4 1 (-96)=100+384=484 0, 2 корня

у=

у=

4.Вернёмся к замене:

х 2 -5х=6 и х 2 -5х=-16

х 2 -5х-6=0 х 2 -5х+16=0

Д=(-5) 2 -4 1 (-6)=49 0, Д=(-5) 2 -4 1 16=-41 ,

2 корня нет корней

х=

х=

-Составим алгоритм решения уравнений, приводимых к квадратным :

Алгоритм решения уравнений, приводимых к квадратным :

Ввести замену переменной.

Составить квадратное уравнение с новой переменной и решить его

Вернуться к замене переменной.

Решить получившиеся уравнения.

Сделать вывод о количестве корней.

2)рассмотрим уравнение 9х 4 -10х 2 +1=0

-Определите степень этого уравнения

-Можно ли решить это уравнение уже изученными способами?

-Для решения уравнений четвёртой степени, имеющих вид ах 4 + b х 2 +с=0 используют метод введения новой переменной. Дадим определение уравнений этого вида.

Уравнения вида ах 4 + b х 2 +с=0 , где а 0, являющиеся квадратными относительно х 2 , называют биквадратными .

Решим уравнение 9х 4 -10х 2 +1=0

1.Введём новую переменную: у=х 2 .

2. Получим уравнение: 9у 2 -10у+1=0

Далее учащиеся самостоятельно решают полученное уравнение в тетрадях , 1 ученик у доски для последующей проверки)

Д=(-10) 2 -4 9 100-36=64

у =

у=

у ₁ = или у ₂ =1

Вернёмся к замене: х 2 = или х 2 =1

х ₁ = ;х ₂ =- х ₃ =1; х ₄ =-1.

Ответ: — ; -1; ;1.

4.Закрепление изученного материала:

работа по учебнику№277(а),№278(а) (используя индивидуальные карточки и с алгоритмом решения уравнений, приводимых к квадратным)

(х 2 +3) 2 -11(х 2 +3)+28=0. Пусть х 2 +3=у

Д=(-11) 2 -4

у=

Вернёмся к замене: х 2 +3=7 или х 2 +3=4

х 4 -5х 2 -36=0. Пусть х 2 =у.

Тогда у 2 -5у-36=0

Д=(-5) 2 —

у=

у=

Вернёмся к замене: х 2 =9 или х 2 =-4

-Дайте определение биквадратного уравнения. Объясните, как решают биквадратные уравнения?

-Уравнения каких степеней мы рассмотрели?

Для курса высшей математики известны формулы для нахождения корней третьей и четвёртой степени, однако они сложны и громоздки и не имеют практического применения. Для уравнений пятой и более высоких степеней формул не существует. Это было доказано в 19 веке Нильсом Абелем и Эваристом Галуа.

анкета для учащихся (смотри приложение)

составить и решить уравнения высших степеней на данные методы решения (по 2 уравнения)

Урок «Целое уравнение и его корни»

Краткое описание документа:

Видеоурок «Целое уравнение и его корни» дает представление о целом уравнении, видах таких уравнений, приведении уравнения к стандартному виду, решении подобных уравнений. Задача данного видеоурока – облегчить усвоение материала по данной теме, формировать умения решать задания, в которых используются целые уравнения, способствовать запоминанию учебного материала.

Оформление наглядного материала в виде урока дает возможность заменить учителя в части подачи стандартного блока нового материала, освободить учителя для углубления индивидуальной работы. Видеоматериал помогает сконцентрировать внимание учащихся на освоении нового материала, помогает глубже его понять и лучше запомнить.

Видеоурок начинается с представления темы урока. На экране отображается определение целого уравнения, содержащего одну переменную, как уравнения, обе части которого представляют собой целые выражения. Ниже приведены примеры таких уравнений: (х 5 -2) 2 +х 3 =х 10 -3(х-2), х 3 (х 3 -36)=2(х+8)-2. Далее рассматривается преобразование уравнений, при котором все его слагаемые переносятся из правой части в левую, раскрываются скобки и приводятся подобные слагаемые. После этого уравнение принимает вид, в котором левая его часть представляет собой многочлен, а правой части – 0. Отмечается, что в ходе преобразований получается уравнение, равносильное данному. К тому же уравнение, к которому приведено исходное, в общем виде можно записать: Р(х)=0, где Р(х) – многочлен стандартного вида.

Рассмотренные примеры подводят к общему выводу о том, что любое целое уравнение, содержащее одну переменную, может быть приведено к виду Р(х)=0, где Р(х) – многочлен, степень которого является степенью данного уравнения. То есть степень некоторого произвольного целого уравнения может быть определена после приведения его к равносильному уравнению вида Р(х)=0 и равна степени многочлена Р(х).

Далее рассматривается уравнение первой степени – такое уравнение, которое приводится к виду ах+b=0 с одной переменной х, числами а и b, при этом а≠0. Корень данного уравнения находится по формулех=-b/a. Отмечается, что такое уравнение имеет один корень.

Также предлагается рассмотреть решение уравнения второй степени, которое приводится к виду ах 2 +bx+c=0, содержащее переменную х, некоторые числа а, b, c, при этом а≠0. Известен способ нахождения корней данного уравнения путем вычисления дискриминанта. На экране отображается формула нахождения дискриминанта для уравнения второй степени: D=b 2 -4ac. В зависимости от значения дискриминанта, может быть два корня уравнения – D>0, один – для D=0, или корни отсутствуют D 3 +bx 2 +cх+d=0 и ах 4 +bx 3 +cх 2 +dх+e=0. В каждом из этих уравнений имеется одна переменная х, коэффициент при старшей степени a≠0, остальные коэффициенты – некоторые числа. Уточняется, что уравнение третьей степени не может иметь более трех корней, а уравнение четвертой степени имеет не более четырех корней. В качестве дополнительной информации ученикам сообщается, что формулы для нахождения корней уравнений третьей и четвертой степени существуют, но они громоздкие и неудобные в применении, а для уравнений пятой степени и выше формул для нахождения корней не существует. Однако решить такие уравнения иногда удается при помощи специальных приемов, которые позволяют упростить выражение и найти корни.

На примере демонстрируется один из способов, как можно найти корни уравнения, не применяя сложных формул нахождения корней.Описывается, каким образом решение некоторых уравнений можно найти с помощью разложения многочлена на множители. Уравнение х 3 -27x 2 -х+27=0 раскладывается на множители, выведя за скобки общий множитель (х-27). В результате преобразований получим произведение (х-27)(х-1)(х+1)=0 Полученное уравнение сводится к нахождению решений трех уравнений х-27, х-1, х+1. Из этих уравнений легко найти корни х₁=27, х₂=1, х₃=-1.

Далее рассматривается еще один способ решения уравнений высокой степени – способ введения новой переменной. Применение способа описывается на примере решения уравнения (х 2 +х-1)(х 2 +х-4)=-2. Сначала все члены уравнения переносятся в левую часть, раскрываются скобки. После данный преобразований получается многочлен стандартного вида 4 степени. Однако, подметив особенность данного уравнения – то, что в исходном уравнении есть одинаковые части х 2 +х, вводим новую переменную для обозначения этого выражения: х 2 +х=у. после подстановки новой переменной в уравнение, получим уравнение вида (у-1)(у-4)=-2. После приведения уравнения к стандартному виду получается обычное квадратное уравнение, корнями которого будут у₁=2, у₂=3. Значение корней у подставим в выражение для определения значения искомых х. Нахождение корней уравнения сводится к решению двух уравнений х 2 +х=2 и х 2 +х=3. В результате вычислений будут найдены корни данных уравнений будут х₁=1, х₂=-2, х₃≈1,3, х₄≈-2,3. Отмечается, что данным способом нередко решают уравнения четвертой степени вида ax 4 +bx 2 +c=0, в которых х является переменной, a, b, c – некоторыми числами, где а≠0. На экране дается определение биквадратного уравнения как уравнения четвертой степени вида ax 4 +bx 2 +c=0са≠0.

Для закрепления полученных знаний о решении уравнений способом введения новых переменных предлагается рассмотреть решение биквадратного уравнения 16х 4 -8х 2 +1=0. Вводится новая переменная у=х 2 . После ее введения образуется квадратное уравнение, имеющее один корень у=0,25. После подстановки значение новой переменной в выражение для ее определения можно найти корни уравнения х₁=0,5 и х₂=-0,5.

Видеоурок«Целое уравнение и его корни» подробно и наглядно представляет учащимся материал по данной теме, поэтому может быть использован учителем не только на уроке в школе, но также при дистанционном обучении, рекомендуется для самостоятельного освоения темы.