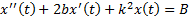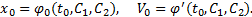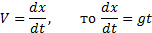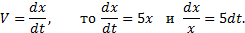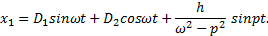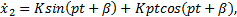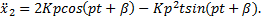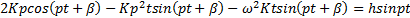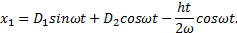Лекции по теме «Дифференциальные уравнения» Е.Н.01 Математика.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Департамент образования и науки Приморского края
Краевое государственное автономное
профессиональное образовательное учреждение
«Региональный технический колледж»
Учебная дисциплина Е.Н.01 МАТЕМАТИКА
Преподаватель высшей квалификационной категории учебной дисциплины
Лекции изложены в доступном пониманию виде и могут быть использованы студентами при самостоятельной подготовке к занятиям.
Изложение теоретического материала по теме сопровождается рассмотрением большого количества примеров и задач, что позволит подготовиться к выполнению практической работы. В конце лекции представлены вопросы, необходимые для самоподготовки и темы для самостоятельного изучения.
Пособие поможет обучающимся освоить тему «Дифференцированные уравнения» курса высшей математики, подготовиться к сдаче зачётов и экзаменов.
Лекции по теме «Дифференцированные уравнения» рекомендованные для всех специальностей в образовательных учреждениях среднего профессионального образования.
Раздел 1. Дифференциальное и интегральное исчисление
Тема 1.2. Обыкновенные дифференциальные уравнения
1.Задачи, приводящие к дифференциальным уравнениям. Общее и частное решение.
2.Дифференциальные уравнения с разделяющими переменными.
3.Линейные дифференциальные уравнения 1 порядка.
4.Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами.
1. Задачи, приводящие к дифференциальным уравнениям. Общее и частное решение.
Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этих функций. Если независимая переменная одна, то уравнение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется уравнением в частных производных.
Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения.
х+ уу’=0 – обыкновенное дифференциальное уравнение 1 порядка.
— 4 xy = — обыкновенное дифференциальное уравнение 2-го порядка.
О: Решением дифференциального уравнения называется такая дифференцируемая функция у=(х), которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.
О: Общим решением дифференциального уравнения 1-го порядка у’= f ( x ;у) в области D называется функция у=(х,С), обладающая следующими свойствами:
1)она является решением данного уравнения при любых действительных значениях произвольной постоянной С;
2)для любого начального условия у(х 0 ) = у 0 такого, что (х 0 ;у 0 ) , существует единственное значение С=С 0 , при котором решение у=(х,С 0 ) удовлетворяет заданному начальному условию.
О: Всякое решение у=(х,С 0 ), получающееся из общего решения у=(х,С) при конкретном значении С=С 0 , называется частным решением.
О: Задача, в которой требуется найти частное решение уравнения у’ = f ( x ; y ), удовлетворяющих начальному условию у(х 0 ) = у 0 , называется задачей Коши.
Построенный на плоскости хОу график всякого решения у=(х) данного дифференциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению (х;С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С, а частному решению, удовлетворяющему начальному условию у(х 0 ) = у 0 , — кривая этого семейства, проходящая через точку (х 0 ;у 0 ).
2. Дифференциальные уравнения с разделяющими переменными
О: Дифференциальное уравнение вида
называется уравнением с разделяющими переменными.
Если f 2 ( x ) ≠ 0 и 1 ( y ) ≠ 0, то его можно представить в виде
В результате почленного интегрирования получаем
Пример 1. Решить уравнение у’ = .
Решение. f 2 ( x ) = x , 1 ( y ) = у, = , ydx = xdy . Разделяя переменные, получаем = . Интегрируя, = + С 1 |, С 1 0 или = + С 1 .
Потенцируя, находим | у| = | С 1 | |х |, что эквивалентно уравнению у = С 1 х. Полагая С 1 = С, окончательно получаем у = Сх.
Пример 2. Найти общее решение дифференциального уравнения
(1 + е 2х ) у 2 dy = е х dx и частное решение, удовлетворяющее начальному условию у(0) = 0.
Решение. Разделим переменные: у 2 dy = . Почленно интегрируя,
Получим : у 3 = arctg е х + С, или у 3 = 3 arctg е х + C , или у = — общее решение дифференциального уравнения.
Найдем постоянную интегрирования С из условия у(0) = 0: 0 = + С или С = — . Частное решение имеет вид: у 3 = 3 arctg е х — ,
Пример 3. Найти общее решение дифференциального уравнения
х + у у ‘ = 0 и частное решение, удовлетворяющее начальному условию у(0) = 2.
Решение. Разделяя переменные и обозначая у’ = , получим
y = — x ydy = — xdx.
Почленно интегрируя, будем иметь = — + С или х 2 + у 2 = С — общее решение дифференциального уравнения. Найдем постоянную интегрирования С из условия у(0) = 2 : 0 + 4 = С С = 4. Частное решение имеет вид х 2 + у 2 = 4.
Замечание. Геометрической интерпретацией общего решения данного уравнения является семейство концентрических окружностей х 2 + у 2 = С
С центром в начале координат. Частное решение представляет собой конкретную окружность х 2 + у 2 = 4, проходящую через точку с координатами (0;2).
3.Линейные дифференциальные уравнения 1 порядка.
О: Дифференциальное уравнение вида у’ + Р(х) у = Q ( x ) называется линейным. Если Q ( x ) 0, то уравнение называется линейным неоднородным, а если Q ( x ) = 0, то – линейным однородным.
Общее решение линейного однородного уравнения у’ + Р(х) у = 0 легко получается разделением переменных
= — P (x) y = — P (x) y = — dx + = — y = C .
Пример 1. Найти общее решение уравнения у’ + 3у = е 2х .
Решение. Данное уравнение является линейным. Здесь р(х) = 3; f (х) = е 2х . Решаем сначала соответствующее однородное уравнение у’ + 3у = 0. Разделяя переменные = — 3 dx и интегрируя, находим
= — 3х + или у = С 1 е -3х = С е -3х .
Общее решение данного неоднородного уравнения будем искать в том же виде у = С(х) е -3х , только произвольную постоянную будем считать уже функцией от х. Здесь применен метод вариации постоянной. Дифференцируя, имеем у’ = С’ (х) е -3х – 3С(х) е -3х . Подставляя в данное уравнение выражения для у и у’, получаем
С’ (х) е -3х = е 2х , С’ (х) = е 5х или dC = е 5х d х, откуда С(х) = е 5х + С 2 , где С 2 – произвольная постоянная. Следовательно, общее решение данного уравнения имеет вид у = С(х) е -3х = ( е 5х + С 2 ) е -3х или у = е 2х + С 2 е -3х .
Найдем теперь общее решение данного уравнения методом подстановки. Положим у = uv . Тогда будем иметь y ‘ = u ‘ v + uv ‘.
Подставляя эти выражения в данное уравнение, получим
u ‘ v + uv ‘ + 3 uv = е 2х или u ‘ v + u ( v ‘ + 3 v ) = е 2х . ()
Теперь потребуем, чтобы выражение в скобках обратилось в нуль, т.е. чтобы v ‘ + 3 v = 0, откуда = — dx ; = — x ; = e — x ; v = e -3 x .
Подставляя найденное значение v в (), найдем u ‘ e -3 x = e 2 x ; du = e 5 x dx ;
u = е 5х + С. Но у = uv , поэтому у = е -3х ( е 5х + С ) или у = е 2х + С е -3х .
Пример 2. Найти общее решение дифференциального уравнения
ху’ + 2у = и частное решение, удовлетворяющее начальному условию
Подставляя у и у’ в исходное уравнение, будем иметь
x v u’ + x u v’ + 2u v = ; u ( x v’ + 2v ) + x v u’ = .
Решим оставшееся уравнение:
x v u’ = xv = x = = 1 du = dx u = x + C.
Общее решение уравнения имеет вид y = u v = .
Найдем частное решение: 1 = С = 6 у = .
4.Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами.
некоторые постоянные действительные числа, называется линейным однородным уравнением второго порядка с постоянными коэффициентами.
Теорема. Если у 1 (х) и у 2 (х) — два линейно независимых частных решения уравнения 0 у» + 1 у’ + 2 у = 0, то у = С 1 у 1 + С 2 у 2 есть общее решение этого уравнения (С 1 и С 2 — произвольные постоянные ).
Теорема. Частное решение линейного однородного уравнения второго порядка с постоянными коэффициентами 0 у» + 1 у’ + 2 у = 0
может быть найдено в виде у = е kx .
Доказательство. После нахождения у’ = k e kx , y » = k 2 e kx и подстановки в уравнение, получим 0 k 2 e kx + 1 k e kx + 2 e kx = 0 e kx ( 0 k 2 + 1 k + 2 ) = 0.
Поскольку е kx 0, то 0 k 2 + 1 k + 2 = 0.
Это квадратное уравнение определит те значения k , при которых у = е kx
будет решением дифференциального уравнения. Оно называется характеристическим уравнением.
Случай 1. Корни k 1 и k 2 квадратного уравнения действительны и различны ( k 1 k 2 ) ( D 0). Получим два частных линейно независимых решения у 1 = ; у 2 = . Общее решение исходного однородного дифференциального уравнения будет иметь вид: у = С 1 + С 2 .
Пример 3. Найти общее решение уравнения у» – 3у’ +2у’ =0.
Решение. Составляем характеристическое уравнение, заменяя у» на k 2 , у’ на k , а у на 1. Получаем k 2 — 3 k + 2 = 0; k 1 = 1; k 2 = 2 y = C 1 e x + C 2 e 2 x .
Случай 2. Корни k 1 и k 2 квадратного уравнения действительны и одинаковы ( k 1 = k 2 = k = — ( D = 0).
В этом случае общее решение имеет вид:
у = C 1 e kx + C 2 х e kx = ( C 1 + C 2 x ) e kx .
Пример 4. Найти общее решение уравнения у» – 2у’ + 1 = 0.
Решение. Соответствующее характеристическое уравнение имеет вид
k 2 – 2 k + 1 =0. Корни уравнения k 1 = k 2 = 1 действительные и равные.
Этим корням соответствуют частные линейно независимые решения
у 1 = е х , у 2 = х е х ; = const . Общее решение уравнения имеет вид
у = С 1 е х + С 2 х е х = е х ( С 1 + С 2 х ).
Пример 5. Найти общее решение уравнения у» – 4у’ + 13 =0.
Решение. Соответствующее характеристическое уравнение имеет вид
k 2 – 4 k + 13 = 0. Корни уравнения k 1 = 2 + 3 i , k 2 = 2 – 3 i — комплексные.
Этим корням соответствуют частные линейно независимые решения у 1 = е 2х cos 3 x , y 2 = = е 2х sin 3 x . Общее решение уравнения имеет вид
у = е 2х ( С 1 cos 3 x + C 2 sin 3 x ).
У кого есть лекции дифференциальные уравнения
Лекция 13. Дифференциальные уравнения и методы их решения
В данной лекции рассматриваются следующие вопросы:
1. Основные понятия и определения.
2. Дифференциальные уравнения первого порядка с разделяющимися переменными.
3. Линейные уравнения второго порядка.
Изучение данных вопросов необходимо для изучения динамики точки, твердого тела и системы.
Основные понятия и определения.
Дифференциальным называется уравнение, содержащее производные неизвестной функции.
Обыкновенным называется такое дифференциальное уравнение, в котором неизвестная функция зависит от одного аргумента, например,
x » t +2 b x ‘ t + k 2 x t = B
Порядком дифференциального уравнения называется порядок наивысшей из производных, входящих в него (уравнение (1) – уравнение второго порядка). Решением дифференциального уравнения называется функция, при подстановке которой в это уравнение последнее обращается в тождество. Частным решением дифференциального уравнения называется любое из возможных его решений. Например, подстановкой в уравнение (1) значения x = А легко убедиться, что оно обращается в тождество при x = А = В/ k 2 . Это и есть одно из его частных решений.
Общим решением дифференциального уравнения называется совокупность всех его частных решений . Если уравнение второго порядка является интегрируемым, т.е. его общее решение можно записать в известных функциях, то оно будет иметь вид: x = φ ( t , C 1 , C 2 ) 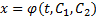
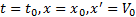
x 0 = φ 0 ( t 0 , C 1 , C 2 ), V 0 = φ ‘ ( t 0 , C 1 , C 2 ).
Дифференциальные уравнения первого порядка с разделяющимися переменными.
Если дифференциальное уравнение может быть представлено в виде Р ( x ) dx = Q ( t ) dt , где функция Р ( x ) зависит только от x , а функция Q ( t ) зависит только от t , то говорят, что переменные разделяются. В этом случае имеем
P x dx = Q t dt + C 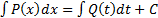
Пример 1. Точка движется прямолинейно со скоростью V = gt ( V в м / c , t в c ). Найти закон ее движения, если при t = 0 x 0 = 1 м.
V = dx dt , то dx dt = gt
и движение точки описывается дифференциальным уравнением с разделяющимися переменными: dx = gtdt . В результате интегрирования получаем: x = gt 2 / 2 + C . Подставив в это уравнение начальное условие x 0 = 1 м при t = 0, получим: С = 1 м. Следовательно, закон движения точки имеет вид: x = ( gt 2 /2 + 1) м.
Пример 2. Точка движется прямолинейно со скоростью V = 5x ( м/ c ). Найти закон движения точки, если при t = 0 x 0 = e ( м) .
V = dx dt , то dx dt =5 x и dx x =5 dt .
В результате интегрирования получаем: ln x = 5 t + C . Используя начальные данные, находим постоянную : С = ln e = 1 м. Следовательно, закон движения точки имеет вид x = e 5 t +1 ( м) .
Линейные уравнения второго порядка.
Линейным уравнением второго порядка называется уравнение вида
x » t + P ( t ) x ‘ t + Q ( t ) x t = R ( t ) 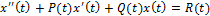
Если правая часть в этом уравнении равна нулю, т.е. R ( t ) = 0, уравнение называется однородным, в противном случае – неоднородным.
Общее решение неоднородного уравнения (2) x ( t ) складывается из общего решения x 1 ( t ) соответствующего однородного уравнения и какого-либо частного решения x 2 ( t ) неоднородного уравнения (2)
Для выполнения индивидуальных заданий необходимо уметь решать дифференциальное уравнение вида
x » t +2 b x ‘ t + k 2 x t = R t (4)
которое является линейным неоднородным уравнением второго порядка с постоянными коэффициентами. Для нахождения общего решения дифференциального уравнения (4) необходимо знать общее решение однородного линейного уравнения
которое ищется в виде x = x 1 = e λt 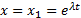
λ 2 =2 b λ + k 2 =0 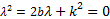
При решении данного уравнения возможны три случая:
1) k b , когда характеристическое уравнение (6) имеет два неравных действительных корня λ 1,2 =- b ± b 2 — k 2 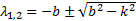
x 1 = C 1 e λ 1 t + C 2 e λ 2 t 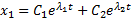
2) k = b, когда характеристическое уравнение (6) имеет два равных корня λ 1 = λ 2 =- b 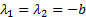
x 1 = C 1 e λ 1 t + C 2 t e λ 2 t 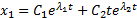
3) k > b , когда характеристическое уравнение (5) имеет два комплексных корня λ 1,2 =- b ± b 2 — k 2 = — b ± i k 1 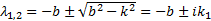
x 1 = C 1 e — bt + i k 1 t + C 2 e — bt — i k 1 t = e — bt ( C 1 e i k 1 t + C 2 e — i k 1 t ) 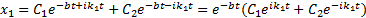
Далее, используя формулу Эйлера, e iα = cosα + isinα 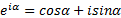
x 1 = e — bt ( D 1 sin k 1 t + D 2 cos k 1 t ) 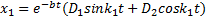
где D 1 , D 2 – некоторые постоянные.
В частном случае, когда b = 0 и k ≠0 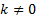
x 1 = D 1 sin k 1 t + D 2 cos k 1 t 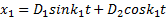
Для нахождения общего решения неоднородного дифференциального уравнения (4) необходимо еще найти какое-либо его частное решение. В индивидуальных заданиях встречаются варианты, в которых R ( t )= A = const и R ( t )= Acos ( pt + α 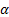
В случае, когда R ( t )= Acos ( pt + α 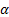
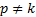
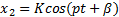
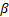
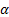
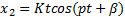
Пример 3. Решить уравнение x + ω 2 x =h sinpt 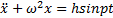
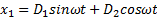
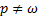
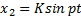
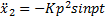
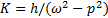
x 1 = D 1 sinωt + D 2 cosωt + h ω 2 — p 2 sinpt .
В случае, когда p = ω 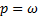
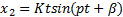
x 2 = Ksin pt + β + Kptcos ( pt + β ),
x 2 =2 Kpcos pt + β — K p 2 tsin ( pt + β ).
Подставляя эти функции в уравнение, находим
2 Kpcos pt + β — K p 2 tsin pt + β — ω 2 Ktsin pt + β =h sinpt
Отсюда, учитывая, что p = ω 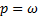
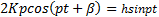
Это уравнение удовлетворяется тождественно, если
β = π /2 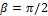
Следовательно, в данном случае общее решение имеет вид
x 1 = D 1 sinωt + D 2 cosωt — h t 2 ω cosωt .
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
http://www.teoretmeh.ru/dinamika13.htm