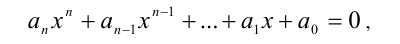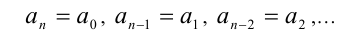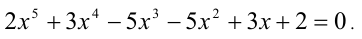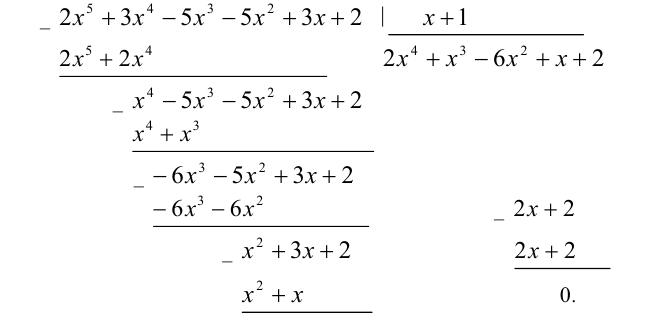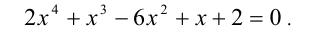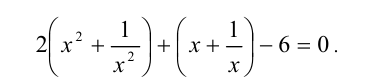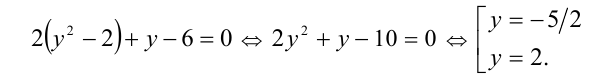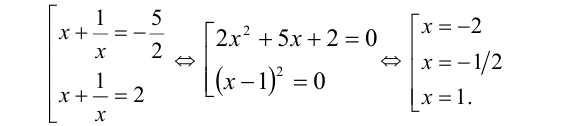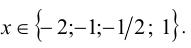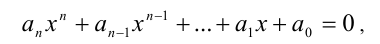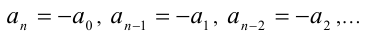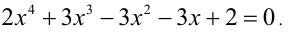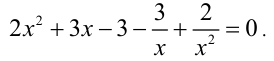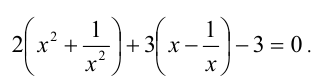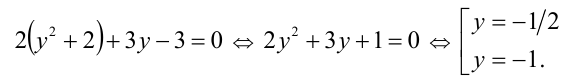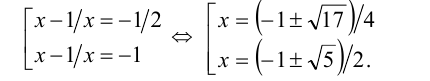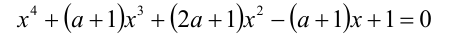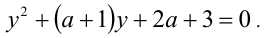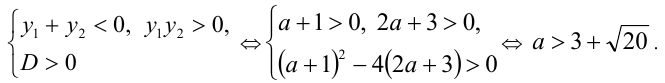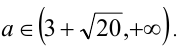Математика. Симметрические уравнения и примеры их решения.
Уравнения называются симметрическими уравнениями 3-й степени, если они имеют вид ах 3 + bx 2 + bх + a = 0.
Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства возвратных уравнений:
— У любого возвратного уравнения нечетной степени всегда есть корень, равный -1.
Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е. (х + 1)(ах 2 + (b – а)x + а) = 0, поэтому, х + 1 = 0 или ах 2 + (b – а)x + а = 0, первое уравнение и доказывает интересующее нас утверждение.
— У возвратного уравнения корней, равных нулю, нет.
в) При делении многочлена нечетной степени на (х + 1) частное является снова возвратным многочленом и это доказывается по индукции.
Уравнения называются симметрическими уравнениями 4-й степени, если они имеют вид ах 4 + bx 3 + сх 2 + bх + a = 0.
Алгоритм решения подобных уравнений таков:
а) Разделить обе части исходного уравнения на х 2 . Это действие не приведет к потере корня, ведь х = 0 решением заданного уравнения не является.
б) С помощью группировки привести уравнение к виду: а(x 2 + 1/x 2 ) + b(x + 1/x) + c = 0.
в) Ввести новую неизвестную: t = (x + 1/x).
Проделаем преобразования:t 2 = x 2 +2 + 1/x 2 . Если теперь выразить x 2 + 1/x 2 , то t 2 – 2 = x 2 + 1/x 2 .
г) Решить в новых переменных полученное квадратное уравнение: аt 2 + bt + c – 2a = 0.
д) Сделать обратную подстановку.
Пример.
6х 4 – 5х 3 – 38x 2 – 5х + 6 = 0.
Решение.
6х 2 – 5х – 38 – 5/х + 6/х 2 = 0.
6(х 2 + 1/х 2 ) – 5(х + 1/х) – 38 = 0.
Вводим t: подстановка (x + 1/x) = t. Замена: (x 2 + 1/x 2 ) = t 2 – 2, имеем:
6t 2 – 5t – 50 = 0.
t = -5/2 или t = 10/3.
Вернемся к переменной х. После обратной замены решим два полученных уравнения:
х 2 – 10/3 х + 1 = 0;
Ответ: -2; -1/2; 1/3; 3.
Симметрические уравнения и системы уравнений в подготовке к ОГЭ по математике
Муниципальное общеобразовательное учреждение «Лицей №3 им. П.А.Столыпина г. Ртищево Саратовской области»
«Симметрические уравнения и системы уравнений в подготовке к ОГЭ по математике»
Ракурс: математический объект
Быков Максим, ученик 9А класса
МОУ «Лицей № 3 им. П.А.Столыпина
г. Ртищево Саратовской области»
Мрыхина Маргарита Владимировна, учитель математики 1 категории
2.1 Симметрические многочлены
2.2 Применение симметрических многочленов в решении задач
2.3 Симметрические уравнения и способы их решения
2.4 Симметрические системы уравнений
Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека, и употреблялось скульпторами ещё в V веке до н. э.
Слово «симметрия» греческое. Оно означает «соразмерность», «пропорциональность», одинаковость в расположении частей и еще под словом «симметрия» понимается неизменность при какой либо операции не только предметов, но и физических явлений, математических формул, уравнений. Математики издавна стремились к красоте математических формул и справедливо считали, что красивая формула отличается от некрасивой тем, что в красоте больше симметрии.
Выдающийся математик Герман Вейль высоко оценил роль симметрии в современной науке:«Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство».
Понятие симметрии в школьном курсе математики изучается на уроках геометрии. Мне стало интересно: а есть ли симметрия в алгебре? Захотелось узнать и понять, как это математическая формула или уравнение является симметричными?
При подготовке к ОГЭ по математике при решении заданий второй части мы встречаемся с решением симметрических уравнений и систем уравнений и
чтобы поглубже разобраться в этом материале я и выбрал тему своей исследовательской работы «Симметрические уравнения и системы уравнений в подготовке к ОГЭ по математике»
Проблема: выяснить, как проявляется симметрия в алгебраических выражениях, уравнениях и системах уравнений
―Рассмотреть, какие выражения, уравнения и системы уравнений являются симметричными и каковы их способы решения.
―потренироваться в решении симметрических уравнений и систем уравнений
Актуальность моего исследования состоит в том, что те знания, которые я получил, я могу применять для решения более сложных задач в математике при подготовке к ОГЭ
―изучить необходимую литературу по выбранной теме
―ввести понятие симметрических многочленов, уравнений и систем уравнений
―рассмотреть решение практических заданий с симметрическими многочленами, рассмотреть решение симметрических уравнений и систем уравнений
― подготовить презентацию и поделиться ею с одноклассниками
2.1. Симметрические многочлены
Многочлен от x и y называют симметрическим, если он не изменяется при замене x на y, а y на x. Многочлен х 2 у+ху 2 — симметрический. А многочлен x 3 + 3y 2 не является симметрическим: при замене x на y, а y на x он превращается в многочлен y 3 + 3x 2 , который не совпадает с первоначальным. Приведу важнейшие примеры симметрических многочленов. Как известно из арифметики, сумма двух чисел не меняется при перестановке слагаемых, т. е. x + y = y + x для любых чисел x и y. Это равенство показывает, что многочлен x + y является симметрическим. Точно так же из переместительного закона умножения xy = yx следует, что произведение xy является симметрическим многочленом. Симметрические многочлены
x + y и xy являются самыми простыми. Их называют элементарными симметрическими многочленами от x и y.
Симметрическими являются следующие алгебраические выражения:
(a+b) 2 =a 2 +2ab+b 2
(a+d) 3 =a 3 +3a 2 b+3ab 2 +b 3
(a+b) 4 =a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4 , такназываемыебиномы .
Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Треугольник можно продолжать неограниченно. Он обладает симметриейотносительно вертикальной оси, проходящей через его вершину
2.2. Применение симметрических многочленов в решении задач
Простейшие симметрические выражения относительно корней квадратного уравнения встречаются в теореме Виета. Это позволяет использовать их при решении некоторых задач, относящихся к квадратным уравнениям. Рассмотрим ряд примеров.
Квадратное уравнение х 2 +рх+ q =0 имеет корни х1 и х2. Не решая этого уравнения, выразить через р и q сумму х1 2 +х2 2 .
Выражение х1 2 +х2 2 ― симметрическое относительно х1 и х2.
Дано квадратное уравнение x 2 + 6x − 10 = 0; составить новое квадратное уравнение, корнями которого являются квадраты корней данного уравнения.
Для решения этой задачи обозначим корни данного уравнения через x1 и x2, корни искомого — через y1 и y2, а коэффициенты искомого уравнения — через p и q. По теореме Виета x1 + x2 =− 6, х1х2= −10 и, также,
По условию задачи, имеем y1= x1 2 , y2= x2 2 , и потому
Таким образом, искомое квадратное уравнение имеет вид:
у 2 − 56y + 100 = 0.
2.3 Симметрические уравнения и способы их решения
В алгебре есть множество различных симметрических уравнений, степень которых 3 и выше. Я остановлюсь на некоторых из них.
1) Уравнение вида (х+а)(х+b)(х+с)(х+d)=А, где а+d=с+b называется симметрическим, например (х+1)(х+2)(х+4)(х+5)=40. Решение такого уравнения заключается в следующем: надо перемножить скобки, для которых выполняется условие а+ d = c + b , т.е. (х+1) умножим на (х+5), а (х+2) умножим на (х+4), тогда уравнение примет вид:
(х 2 +6х+5)(х 2 +6х+8)=40
Пусть у=х 2 +6х, тогда получим (у+5)(у+8)=40, у 2 +9у+40−40=0,
у(у+9)=0, откуда у=0 и у=−9
Произведя обратную замену, получим два уравнения
х 2 +6х=0 и х 2 +6х=−9, решая которые получим что х1=0, х2=−6, х3=−3.
Таким образом, корнями исходного уравнения являются числа: −6; −3; 0.
2) Уравнения вида ах 3 +bх 2 +bх+а=0, где а≠0 также называется симметрическим .
Часто решение таких уравнений сводится к преобразованию левой части этого уравнения в произведение.
Рассмотрим решение уравнения х 3 +2х 2 +2х+1=0
(х 3 +1)+(2х 2 +2х)=0, (х+1)(х 2 −х+1)+2х(х+1)=0, (х+1)(х 2 −х+1+2х)=0
(х+1)(х 2 +х+1)=0, откуда получим, что корнем уравнения является число −1.
При решении симметрических уравнений полезно знать следующее:
У любого симметрического уравнения нечетной степени всегда есть корень равный ―1.
У симметрических уравнений корней, равных нулю нет.
Если степень уравнения выше, чем 3, то способ решения другой .
Уравнение вида ах 4 + b х 3 +сх 2 + b х + а =0, где а≠0 − это симметрическое уравнение
2х 4 +7х 3 +9х 2 +7х+2=0.
Т.к. х=0 не является корнем уравнения, то разделим уравнение на х 2 , получим
2(х 2 + ) + 7 (х+ ) +9=0. Введем замену у= х+ , тогда х 2 + = у 2 −2, получим:
2у 2 +7у+5=0, это квадратное уравнение, его корни будут у1=−1 и у2=−2,5
Выполним обратную замену:
Решая эти уравнения, окончательно получим, что х=2 и х=0,5.
2.4. Симметрические системы уравнений
Система называется симметрической, если f(x, y) и g(x, y) — симметрические многочлены. Для решения симметрических систем пользуются заменой u = x + y, v = xy.
Решим систему уравнений:
Введем замену х+у= u , ху= v , получим
2 u =12, u =6, тогда v =5.
Выполним обратную замену:
Х=6―у, тогда ( 6―у )·у=5, решая это уравнение, получим у=5 и у=1, тогда соответственно х=1, у=5.
Рассмотрим решение системы :
Заменим х+у = u , ху = v , получим
Решая первое уравнение системы, получим v = ―4 и v =―3, тогда соответственно u =―1 и u =―2.
Выполняя обратную замену, получим совокупность систем
Рассмотрим следующую систему:
Введем замену х+у= u , ху= v
(х+у) 2 =х 2 +2ху+у 2 х 2 +у 2 = (х+у) 2 −2ху= u 2 −2 v , тогда получим
U 2+ u -72=0, откуда u =8 u = -9, тогда соответственно v=15, u=32.
Делая обратную замену, получим совокупность систем
Ответ: (3 ; 5 ), ( 5; 3 )
Выполняя данную работу, я узнал, что такое симметрические многочлены, уравнения, системы уравнений, остановился на решении некоторых симметрических уравнений и систем уравнений. Укрепил свои знания в решении симметрических уравнений и систем уравнений. Это позволит мне более качественно подготовится к выполнению заданий 2 части ОГЭ по математике.
Практическая значимость данной работы заключается в следующем:
я, изучив данный вопрос, получил дополнительные знания в области математики, укрепил свой интерес к этой науке.
Работа по данной теме оказалась интересной и полезной.
Болтянский В.Г. и др. Симметрия в алгебре. — М.: Наука, 1967.
Башмаков М.И. Уравнения и неравенства. — М.: Наука, 1971.
Черкасов О.Ю. и др. Математика: Справочник для старшеклассников и поступающих в вузы. — М.: АСТ-Пресс, 2001.
Симметрические и кососимметрические уравнения
Симметрические и кососимметрические уравнения
Симметрическим уравнением n -й степени называется алгебраическое уравнение вида
где равноотстоящие от концов многочлена коэффициенты равны, т.е.
Рассмотрим отдельно решение симметрических уравнений чётной и нечётной степеней [30].
Если 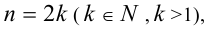
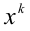
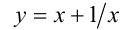
Если же 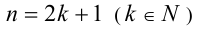
Пример №189.
Решить уравнение
Решение:
Очевидно, имеем симметрическое уравнение 5-й степени. Решаем его по изложенной выше схеме. Одним из корней уравнения будет число x = — 1. Найдём другие корни:
Решим симметрическое уравнение 4-й степени
Поделим для этого обе части уравнения на 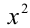
Обозначим у = x + (1/x), тогда
Выполняя обратную подстановку, получаем
Объединяя полученные решения, приходим к ответу:
Кососимметрическим уравнением n -й степени называется уравнение вида
где равноотстоящие от концов многочлена коэффициенты являются противоположными числами, т.е.
Решение кососимметрических уравнений чётной и нечётной степени во многом аналогично решению соответствующих симметрических уравнений.
Если 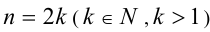
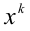
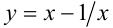
Если же 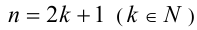
Пример №190.
Решить уравнение
Решение:
Это кососимметрическое уравнение 4-й степени. Поскольку x = 0 не является корнем уравнения, то поделим обе его части на 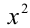
Перепишем последнее уравнение в виде
Положим у = х — (1/x), тогда получим
Выполняя обратную подстановку, получаем 4 решения
Пример №191.
Найти все значения параметра а , при которых уравнение
на промежутке 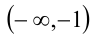
Решение:
Так как 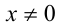
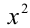
Поскольку функция у =x — (1/x) возрастает на промежутке 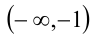
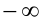
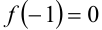
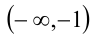
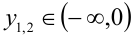
Ответ:
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://www.prodlenka.org/metodicheskie-razrabotki/262653-simmetricheskie-uravnenija-i-sistemy-uravneni
http://lfirmal.com/simmetricheskie-i-kososimmetricheskie-uravneniya/