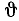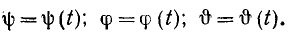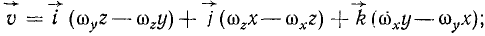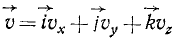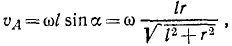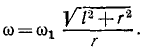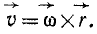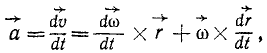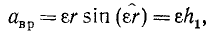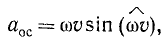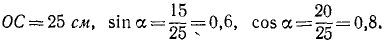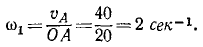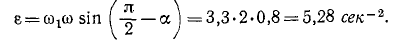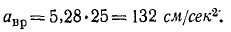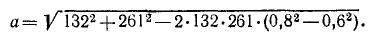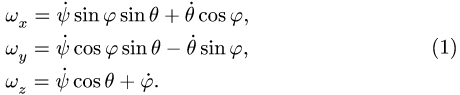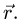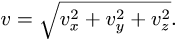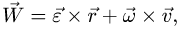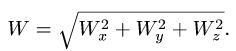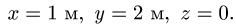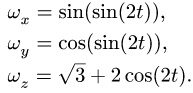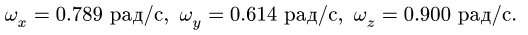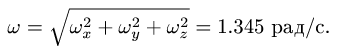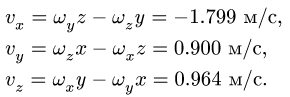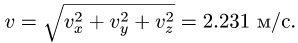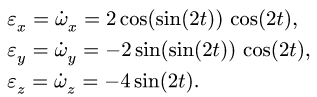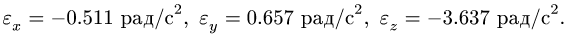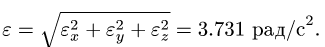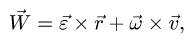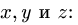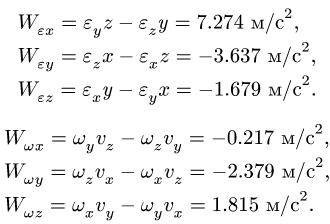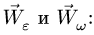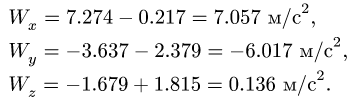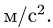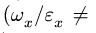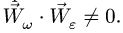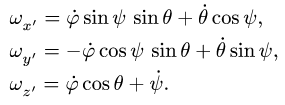Углы эйлера кинематические уравнения эйлера

Сферическое движение твердого тела в теоретической механике

Содержание:

Сферическое движение твердого тела:

Сферическим называют такое движение твердого тела, при котором точки тела описывают траектории, лежащие на сферах с одним и тем же неподвижным центром

Вращение тела вокруг точки

Пусть во время движения тела одна из его точек остается неподвижной. Тогда всякая другая точка тела может двигаться только по поверхности сферы, описанной вокруг неподвижной точки радиусом, равным расстоянию этой точки от неподвижной. Такое движение называют сферическим движением тела, или вращением вокруг неподвижной точки.

Положение тела, имеющего неподвижную точку, можно определить тремя независимыми углами

Углы Эйлера

Чтобы определить положение тела, имеющего неподвижную точку, построим две системы координатных осей с общим началом в этой точке О: основную xOyz и подвижную x’Oy’z’, неизменно связанную с движущимся телом (рис. 107). Три оси подвижной системы составляют 9 углов с тремя осями основной, но для определения положения тела, имеющего неподвижную точку, нет необходимости знать все 9 направляющих косинусов, так как они связаны известными из аналитической геометрии соотношениями, и независимых величин остается только три.

Положение тела, имеющего неподвижную точку, можно определить тремя независимыми углами. Эти углы обычно называют эйлеровыми.1 Ознакомимся с углами, предложенными Эйлером и применяемыми в астрономии, в гироскопии и во многих других науках.

Линией узлов называют линию ON пересечения плоскостей xОy и х’Оу’ основной и подвижной систем. Первый угол — угол прецессии ψ—лежит в плоскости хОу между неподвижной осью Ox и линией узлов. Его измеряют от оси Ox к оси ON против хода часов, если смотреть с оси Oz.

Второй—угол собственного вращения φ—лежит в плоскости х’Оу’ и его отмеривают от линии узлов до оси Ox’ против хода часовой стрелки, если смотреть с оси Oz’. Третий — угол

Во время движения тела эти углы изменяются. Чтобы задать уравнение сферического движения, надо представить их как некоторые непрерывные однозначные функции времени:

Предельное положение такой оси, вокруг которой следует повернуть твердое тело на бесконечно малый угол, чтобы перевести его из одного положения в другое, бесконечно близкое первому, называют мгновенной осью вращения

Мгновенная ось вращения

Положение тела в пространстве можно определить различными способами. В частности, для этого можно задать положение трех его точек. Применим этот способ для изучения сферического движения тела. За одну из этих точек примем неподвижную точку О (рис. 108, а), а две другие, А и В, выберем произвольно, но с условием, чтобы их скорости не были параллельны между собой.

Рассмотрим сначала точку А. Проведем прямую через точку А и неподвижную точку О. Согласно основной теореме кинематики твердого тела (77) проекции скоростей точек А и Q на АО должны быть равны. Но скорость точки О, а потому и ее проекция равны нулю. Скорость точки А нулю не равна, но проекция ее на ЛО должна равняться нулю, следовательно, скорость точки А перпендикулярна к АО. Если мы проведем через точки А и О плоскость (рис. 108, б) перпендикулярно к скорости точки А, то по той же теореме скорости точек этой плоскости должны быть перпендикулярны к прямым, соединяющим эти точки с неподвижной точкой О, т. е. перпендикулярны плоскости.

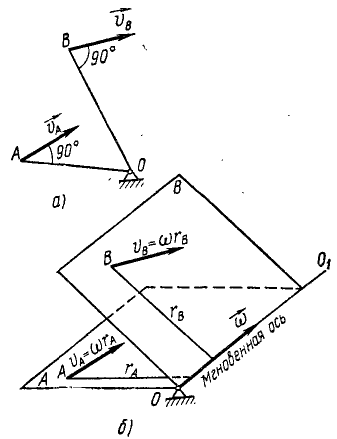
Рис. 108

Рассмотрим теперь точку В и повторим те же рассуждения. Если мы проведем через точки В и О плоскость В перпендикулярно к скорости точки В, то скорости точек этой плоскости должны быть перпендикулярны к плоскости В. Точки, лежащие на линии OO₁ пересечения плоскостей А и В, должны иметь скорости, перпендикулярные сразу к обеим пересекающимся плоскостям, что невозможно. Следовательно, скорости точек этой прямой OO₁ в данное мгновение равны нулю. Мы пришли к убеждению, что при движении тела с одной неподвижной точкой через эту точку всегда можно провести ось, скорости точек которой в данное мгновение равны нулю. Эту ось называют мгновенной осью вращения.

Если в движущемся теле существует ось, скорости точек которой в данное мгновение равны нулю, то скорости других его точек должны быть пропорциональны их расстояниям от оси. Таким образом, картина распределения скоростей в теле с одной неподвижной точкой оказалась на данное мгновение такой же, как и в теле, вращающемся вокруг неподвижной оси.

При изучении вращения тела вокруг неподвижной оси мы условились о направлении вектора угловой скорости. То же условие сохраняется на сферическое движение, где вектор угловой скорости ω направлен от неподвижной точки О по мгновенной оси вращения в такую сторону, чтобы вращение тела представлялось происходящим против хода часов, если смотреть с конца вектора ω, к точке О. Этот вектор можно переносить вдоль оси вращения, но нельзя перемещать параллельно оси. Глубокое отличие вектора угловой скорости при сферическом движении заключается в том, что он постоянно меняет свое направление.

В связи с этим другое толкование принимает и угловое ускорение. Изображая угловое ускорение тела при вращении вокруг оси вектором, мы направляли его в ту или иную сторону по вектору угловой скорости. При вращении тела относительно неподвижной точки дело обстоит иначе: направление угловой скорости меняется. Мы будем называть вектором углового ускорения тела вектор, характеризующий изменение в данное мгновение величины и направления угловой скорости тела

(97)

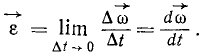
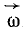
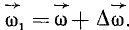
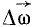
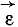
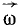
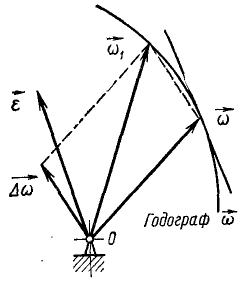
Направление этого вектора, вообще говоря, не совпадает с мгновенной осью вращения. Пусть, например, угловая скорость тела, имеющего неподвижную точку О (рис. 109) и не показанного на чертеже, в данное мгновение равна , а через малый промежуток времени Δt станет Разделив на Δt, мы получим вектор среднего углового ускорения тела. Если мы будем уменьшать промежуток времени Δt, оставляя неизменным его начало, то вектор среднего углового ускорения тела будет стремиться к своему предельному значению — вектору углового ускорения тела. Этот вектор проходит через неподвижную точку О и параллелен касательной к годографу вектора.

Рис. 109

При сферическом движении тела подвижный аксоид катится без скольжения по неподвижному

Аксоиды при сферическом движении

Положение мгновенной оси в теле, имеющем одну неподвижную точку, непрерывно меняется. Но в каждое мгновение ось имеет вполне определенное положение и всегда проходит через неподвижную точку О. Геометрическое место мгновенных осей вращения, проведенных в теле, представляет собой некоторую коническую поверхность и называется подвижным аксои-дом. Положение мгновенной оси вращения можно отметить и относительно неподвижных координат. Их геометрическое место относительно неподвижных координат, называемое неподвижным аксоидом, также является конической поверхностью с вершиной в той же неподвижной точке О. Оба конуса соприкасаются по мгновенной оси вращения. Сферическое движение тела можно представить как качение без скольжения подвижного аксоида по неподвижному.

Зависимость между проекциями скоростей точек тела, их координатами и проекциями угловой скорости выражается формулами Эйлера

Формулы Эйлера

Как было только что показано, скорость каждой точки K тела, имеющего неподвижную точку О, перпендикулярна к прямой КО и пропорциональна расстоянию KО sin α точки К от мгновенной оси вращения (рис. 110), т. е.

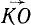
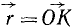
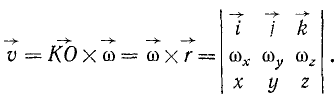
Таким образом, при сферическом движении, как и при вращательном, скорость всякой точки тела можно рассматривать как момент вектора угловой скорости тела относительно этой точки. Проведем из какой-либо точки К тела вектор в неподвижную точку О, принятую нами за начало отсчета. Этот вектор равен по модулю, но направлен противоположно радиусу-вектору точки K относительно начала отсчета О. Момент вектора угловой скорости относительно точки K представим векторным произведением и запишем в виде определителя третьего порядка, как это мы делали (см. 17 и 17′) в статике при определении момента силы:

Раскладывая этот определитель по элементам первой строки:

раскладывая скорость точки по осям координат:

и сравнивая оба равенства, мы можем выразить проекции скорости точки через проекции угловой скорости тела и координаты точки:

(98)

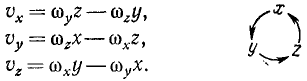
Эти соотношения, очень напоминающие знакомые нам выражения (23) момента силы относительно оси, отличаются от них не только тем, что вектор силы заменен вектором угловой скорости, но и знаками. Круговой заменой букв в любой из трех формул (98) можно получить две остальные. Эти формулы имеют применение при определении проекций скоростей точек тела, совершающего сферическое движение или вращение вокруг неподвижной оси. В частном случае, если тело вращается вокруг оси Oz, то проекции угловой скорости ω_x = ω_y = 0, a ω_z=ω, мы получаем формулы (89).

Задача №1

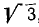
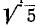
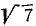
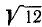
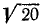
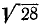
Тело движется вокруг неподвижной точки — начала координат. В некоторое мгновение угловая скорость его изображается вектором, проекции которого на координатные оси равны , , . Найти скорость точки К тела, определяемой координатами , ,.

Решение. Подставляя данные в формулы Эйлера, получим

Ответ. υ = 0. В этот момент времени мгновенная ось проходит через точки О и К.

Задача №2

Ось OA мельничного бегуна (рис. 111) вращается равномерно вокруг вертикальной оси с угловой скоростью ω₁. Длина оси OA=l, радиус бегуна равен r. Пренебрегая скольжением бегуна, определить вектор его угловой скорости.

Решение. Движение бегуна можно рассматривать как вращение около неподвижной точки О. Бегун катится без скольжения, поэтому скорость точки C соприкосновения его с горизонтальной плоскостью равна нулю, и, следовательно, в каждое мгновение ось, проходящая через точки О и С, есть мгновенная ось вращения. Центр бегуна (точка А) движется вокруг вертикальной оси, проходящей через О, с постоянной по величине скоростью

Но точка А принадлежит бегуну, а потому ее скорость в то же время является вращательной скоростью вокруг мгновенной оси вращения ОС. Опуская из А перпендикуляр на мгновенную ось, получаем

где ω—угловая скорость бегуна, а а — угол AОС. Из двух выражений υ_A находим ответ.

Ответ.

Ускорение всякой точки тела, совершающего сферическое движение, состоит из вращательного и осестремительного ускорений

Чтобы получить ускорение какой-либо точки К тела, находящегося в сферическом движении, продифференцируем по времени вектор ее скорости

(99)

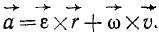
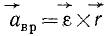
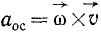
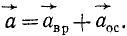
Таким образом, ускорение каждой точки К тела, имеющего одну неподвижную точку О, состоит из векторной суммы двух ускорений: вращательного ускорения и осестремительного ускорения
. В общем случае оба эти ускорения не перпендикулярны друг другу, что необходимо учесть при их суммировании (рис. 112, а).

(99 / )

Эту формулу называют формулой Ривальса.

Чтобы лучше уяснить чему равны и как направлены эти ускорения, обратимся к чертежу.

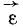
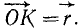
Вращательное ускорение (рис. 112, б) выражается векторным произведением углового ускорения и радиуса вектора Следовательно, оно направлено перпендикулярно плоскости, образованной этими векторами, и по модулю равно

где h₁—длина перпендикуляра, опущенного из точки К на прямую, по которой направлено угловое ускорение ε. Из формулы (100) в частности следует, что эта прямая обязательно должна проходить через неподвижную точку О, потому что в противном случае точка О имела бы неравное нулю вращательное ускорение, т. е. стала бы подвижной.

Осестремительное ускорение по модулю равно

но этот синус равен единице, так как векторы угловой и вращательной скорости взаимно перпендикулярны. Модуль же вектора вращательной скорости υ = ωh, где h—длина перпендикуляра, опущенного из точки К на мгновенную ось вращения, а потому

Направлено осестремительное ускорение перпендикулярно векторам угловой скорости тела и вращательной скорости точки К, т. е. по прямой h от точки К к мгновенной оси вращения.

Задача №3

Найти скорость и ускорение точки В конического катка, равномерно катящегося без скольжения по горизонтальной конической кольцевой опоре (рис. 113). Диаметр катка BC = 30 см, OA = 20 см, скорость центра катка υ_А = 40 см/ceκ и направлена перпендикулярно плоскости чертежа на читателя.

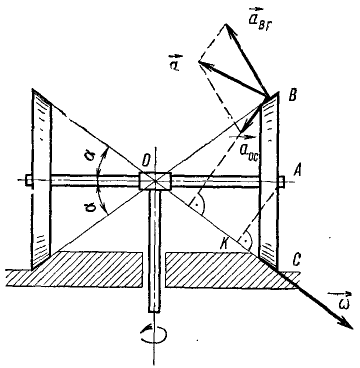
Рис. 113

Решение. Мгновенная ось проходит через неподвижную точку О и точку С, скорость которой в данное мгновение равна нулю, потому что каток катится без скольжения. Вектор угловой скорости ω направлен по мгновенной оси. Модуль его определим, разделив скорость точки А на расстояние АК от мгновенной оси. Из треугольника OAC находим OC 2 = OA 2 + АС 2 = 625. Тогда

Имея эти данные, находим угловую скорость:

Чтобы найти скорость точки В, надо угловую скорость помножить на расстояние точки В от мгновенной оси h = OB sin 2α =25 . 2 . 0,6 . 0,8 =24 см. Скорость точки В перпендикулярна плоскости чертежа, направлена на читателя и по модулю равна 79,2 см/сек.

Найдем теперь вектор углового ускорения. Каток катится равномерно, величина угловой скорости не изменяется, но меняется ее направление, и конец вектора угловой скорости описывает годограф—окружность радиуса ω sin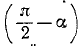. Угловая скорость ω₁, с которой поворачивается вектор угловой скорости ω, равна угловой скорости, с которой поворачивается ось OA во время движения катка:

Вектор углового ускорения равен скорости годографа вектора угловой скорости. Он направлен перпендикулярно плоскости чертежа на читателя, но приложен в неподвижной точке О:

Чтобы определить вращательное ускорение точки В, надо помножить угловое ускорение в на длину перпендикуляра h₁ -BO = 25 см:

Направлен вектор вращательного ускорения перпендикулярно вектору углового ускорения и плечу ВО и в такую сторону, чтобы вектор е указывал против хода часовой стрелки, если смотреть с конца вектора а_вр . Следовательно, вектор а_вр лежит в плоскости BOC и перпендикулярен ВО.

Осестремительное ускорение по модулю равно произведению квадрата модуля угловой скорости на длину перпендикуляра h, опущенного из точки В на мгновенную ось, и направлено к оси:

α_oc = 3,3 2 ∙24 = 261 см/сек.

Угол между векторами вращательного и осестремительного ускорений равен 2α. Полное ускорение точки В определим, применив теорему косинусов

Ответ: υ_B= 79 см/сек, а_в = 257 см/сек 2 .

Скорость и ускорение точки тела

Постановка Задачи. Твердое тело совершает сферическое движение по закону, заданному в углах Эйлера 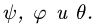Найти скорость и ускорение точки, положение которой дано относительно подвижных осей координат.

1. Воспользуемся кинематическими уравнениями Эйлера для определения проекций угловой скорости на подвижные оси координат

2. Находим проекции скорости 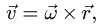на подвижные оси относительно которых задан радиус-вектор точки

3. Вычисляем модуль скорости

4. Дифференцируя по времени t проекции угловой скорости, получаем компоненты углового ускорения 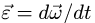в подвижных осях.

5. Ускорение точки представляем в виде векторной суммы

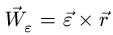
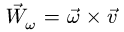
где — вращательное, a — осестремительное ускорение.

6. Находим модуль ускорения

Пример. Твердое тело совершает сферическое движение по закону, заданному в углах Эйлера 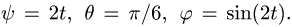При t = 1 с найти скорость и ускорение точки, положение которой относительно подвижных координат задано координатами

Углы 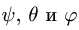даны в рад. Решение

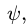
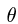
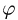
1. Зная зависимости угла прецессии угла нутации и собственного вращения от времени, воспользуемся кинематическими уравнениями Эйлера (1) для определения проекций угловой скорости на подвижные оси координат. Подставляя в (1) заданные функции, получаем

При t = 1 вычисляем

Модуль угловой скорости тела

2. Вычисляем проекции скорости точки на подвижные оси:

3. Модуль скорости точки

4. Дифференцируя пo t проекции угловой скорости, получаем компоненты углового ускорения тела в подвижных осях:

При t = 1 получаем

Модуль углового ускорения

5. Ускорение точки представляем в виде векторной суммы:

Гл. 10. Сферическое движение тела

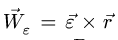
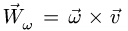
где — вращательное, a — осестремительное ускорение. Вычисляем отдельно их проекции на оси

Компоненты ускорения получаем, суммируя

6. Модуль ускорения 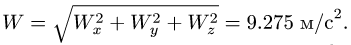Ответы занесем в таблицу. Скорости — в м/с, ускорения — в

Замечание 1. При сферическом движении тела векторы угловой скорости и углового ускорения не лежат на одной прямой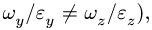а вектор осестремительного ускорения в общем случае не перпендикулярен вектору вращательного ускорения. В этом можно убедиться, вычислив скалярное произведение

Замечание 2. Кинематические уравнения Эйлера для определения проекций угловой скорости на неподвижные оси координат имеют вид

• Плоско-параллельное движение твердого тела
• Движение твердого тела, имеющего неподвижную точку
• Движение твердого тела
• Сложение движений точки
• Произвольная пространственная система сил
• Центр параллельных сил и центр тяжести
• Поступательное движение твердого тела
• Вращение твердого тела вокруг неподвижной оси

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Кинематические уравнения Эйлера и зависимость проекции вектора угловой скорости

Кинематические уравнения Эйлера

• Установить зависимость проекции вектора угловой скорости на неподвижные оси на теле, углы Эйлера , 0, p и их производные по времени. Определяется тремя углами Объект с фиксированной точкой O движется относительно координатной оси Ox1yizi (рис. 136). Система движущихся осей Oxyz прикреплена к движущемуся телу, и ее движение характеризует движение рассматриваемого тела относительно оси Oxlylzl.

Положение движущейся системы координат относительно неподвижной системы координат и, следовательно, положение самого движущегося тела Эйлера: , 0, p Изменение угла прецессии относительно оси Ox и линии узла, являющегося пересечением координатной плоскости и Ohu соответственно ОК Это означает, что угловая скорость fG направлена вдоль этой оси, а тело вращается вокруг оси прецессии Oz, перпендикулярной линии, образующей угол.

Нахождение фигуры равновесия нити на поверхности в случае, когда существует силовая функция, также приводится к определению максимума или минимума некоторого определенного интеграла. Людмила Фирмаль

Когда угол сочленения 0 между осями координат Oz и Oz изменяется, тело вращается вокруг линии узлов OK, перпендикулярных этим осям, с угловой скоростью b. d единичный вектор, направленный на положительную сторону линии узла. Если соответствующий угол поворота , образованный осью координат Ox и узловой линией OK, изменяется, объект, угловая скорость которого pk и 1c является единичным вектором оси Oz, центрируется на соответствующей оси Oz вращения, перпендикулярной этим линиям. Вращение происходит.

При изменении углов Эйлера , 0 и движение тела можно рассматривать как комплекс, состоящий из трех поворотов вокруг пересекающихся осей Oz OK и Oz угловых скоростей bj и e соответственно. Комбинация этих трех вращений соответствует вращению тела вокруг мгновенной оси с угловой скоростью d, направленной вдоль этой оси. По теореме о сложении вращения вокруг пересекающихся осей d = ^ 1 + 0 + + (16) Определяет проекцию вектора угловой скорости th на подвижную координатную ось Oxyz, прикрепленную к телу.

• Движение тела рассматривается относительно фиксированной системы отсчета Ox, y, z. При проецировании векторной суммы справа от (16) на оси Oxyz каждый член вектора должен проецироваться на эти оси. Вектор угловой скорости c 1c ориентирован вдоль оси Oz и перпендикулярен двум другим осям Ox и Oy, что дает этой оси проекцию, равную p. Рис. 137 Ох и ах на оси Угловая скорость 0i, направленная вдоль линии узла, находится в плоскости осей переноса Ox и Oy, проекция на ось Ox равна 0cos p, а проекция на ось Oy ( 0sin p).

Знак минус для проекции на ось Oy установлен потому, что расположение оси, показанное на рисунке, имеет отрицательный компонент, когда вектор 0p разложен. Направление оси Oy. Вектор проекции 0 перпендикулярен оси Oz, а проекция на эту ось равна нулю. Чтобы спроецировать вектор фА , Сначала его нужно разложить на две вертикальные составляющие на координатной оси Oxyz. Один ориентирован вдоль оси Oz, а другой в плоскости вертикальных осей Ox и Oy. У нас есть = pcos0 + sin0 (17) Где T единичный вектор в направлении вдоль линии OL. При проецировании вектора fG каждый вектор с правой стороны (17) должен проецироваться на эти оси на осях координат. Вектор fso0 k дает проекцию x cos0 только на ось Oz.

Наоборот, по закону равенства действия и противодействия, рука будет испытывать со стороны точки давление, направленное вниз и равное абсолютному весу по интенсивности и направлению. Людмила Фирмаль

Осталось спроецировать вектор 0 нахождения в плоскости координатных осей Ox и Oy. На этих осях. Поскольку линии узла перпендикулярны координатным осям Oz и Ozt и, таким образом, также перпендикулярны линиям, линия узла OK также располагается в плоскости этих осей (рис. 1371, линия OL, на которую направлен вектор проекции sin0 T, и Линии узлов перпендикулярны друг другу), поскольку угол p между осями OL Ox и OK, расположенными в плоскости этих осей, представляет собой угол между осями Oy и OL, перпендикулярными им Проекция вектора fwO Г на Oy равна i sin0cos p, а ось Oh— isin0sin p.

Рассматривая проекцию вектора, полученную из правой части (17), объединяя проекции на оси координат векторов, содержащихся в правой части (16), получается уравнение движения Эйлера. Косинус угла оси прецессии Ozt выражается с помощью координатной оси Oxyz, прикрепленной к движущемуся телу через угол Эйлера. Вектор угловой скорости направлен вдоль оси прецессии Ozt. Следовательно, коэффициент в уравнении Сожа является вычисленным косинусом вышеуказанного угла. Покажите их для краткости, 2, 3, y = cos (z ,, Ax) = sin0sin p; Y2 = cos (z1 ,, p) = sin0cos p; (18) y3 = cos (z, Az) = cos0.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Магия тензорной алгебры: Часть 12 — Параметры Родрига-Гамильтона в кинематике твердого тела

Введение

Наконец-то мы подошли к довольно интересной теме — выбору параметров, однозначно определяющих ориентацию твердого тела в пространстве. Исторически наиболее популярными являются углы поворота — они в первую очередь упоминаются в классических учебниках теоретической механики.

Рис.1. Углы Эйлера — параметры, знакомые каждому, кто занимался компьютерной графикой и моделированием пространственного движения тел. И каждый, кому они знакомы, знает, насколько проблематичным бывает их использование.

Обычно углы поворота используют совместно с декартовой системой координат, при этом говорят, что связанная система координат может быть совмещена с базовой путем трех последовательных поворотов вокруг её осей. При этом каждый следующий поворот осуществляется вокруг оси, полученной после предыдущего поворота. Кроме того, следующий поворот не должен происходить вокруг оси, относительно которой совершен предыдущий поворот. В связи с этим существует 12 различных комбинаций углов поворота, самыми известными из которых являются углы Эйлера (рисунок 1). Базовую систему координат поворачивают на угол вокруг оси Z (угол прецессии), затем на угол вокруг оси X (угол нутации), и снова вокруг оси Z на угол (угол собственного вращения) до совмещения её со связанной системой координат.

Использование углов Эйлера всем хорошо — их число совпадает с числом вращательных степеней свободы твердого тела, а значит они не порождают избыточных уравнений связей. Но, даже не прибегая к громоздким формулам, по рисунку 1, можно догадаться, где кроется проблема.

Рис. 2. Знаменитые кинематические уравнения Эйлера. Я, в своё время, хлебнул с ними долгих и кропотливых отладок

Существует два значения угла нутации, при которых происходит вырождение кинематических уравнений Эйлера (рисунок 2) — и . Предположим, что угол нутации принял одно из этих значений — тогда угол прецессии и угол собственного вращения описывают поворот вокруг одной и той же оси Z и принципиально неразличимы друг от друга. При использовании кинематических уравнений Эйлера мы получаем ноль в знаменателе и NaN в фазовых координатах. Приплыли, процедура интегрирования рухнула.

Другой вариант углов поворота — самолетные углы: — рыскание, — тангаж и — крен (рисунок 3).

Рис. 3. Самолетные углы — один из практических способов определения ориентации летательного аппарата в пространстве

Данные параметры поворота вырождаются при тангажах , при этом неразличимы становятся крен и рыскание. Матерые симуляторщики знают, как сходит с ума КПП при выходе на крутые тангажи.

Все возможные комбинации углов поворота имеют вырождение. Для моделирования и закладки в алгоритмы систем управления ориентацией область их применения ограничивается критическими значениями параметров. В прошлой статье мы показали, что не подходят и параметры конечного поворота, а использование непосредственно компонентов тензора поворота затрудняется излишне глубокими зависимостями между ними, что порождает высокий порядок системы уравнений движения.

Однако, ещё великий Леонард Эйлер ввел в рассмотрение четыре параметра, которые не имеют вырождения. На его публикацию по этому поводу тогдашний научный мир особого внимания не обратил. Данная идея, независимо от Эйлера была развита Олидом Родригом, а в работах Уильяма Гамильтона получила окончательное теоретическое обоснование. Встречайте —

1. Кватернионы и действия над ними

Кватернионом называют число вида

где называют компонентами кватерниона. Сами числа (1) образуют множество гиперкомплексных чисел , включающее в себя все действительные числа и множество комплексных чисел . Математики эпохи, когда работал Гамильтон, уже знали о комплексных числах и о том, как построенные на их основе методы позволяют решать задачи планиметрии и естественным было желание расширить понятие комплексного числа для применения подобных методов к пространственным задачам. Проблема была в том, что добавление второй мнимой единицы не решало проблемы. Гамильтону пришла в голову мысль, что подобные расширенные комплексные числа могут быть не трех-, а четырехкомпонентными. Работая в этом направлении, в порыве вдохновения на одной из прогулок он вывел правило умножения таких чисел, что окончательно сложило мозаику новорожденной теории.

Так вот, перемножение кватернионов сводится к алгебраической операции перемножения сумм, с той лишь разницей, что требуется определить правила умножения мнимых единиц. Традиционно, каждая из мнимых единиц возведенная в квадрат дает -1

а их попарные произведения хорошо описываются диаграммой

Рис. 4. Диаграмма перемножения мнимых единиц в кватернионе

смысл которой прост — если перемножать пары мнимых единиц в порядке, указанном стрелкой, то получается третья мнимая единица со знаком «+». Если порядок перемножения изменить на противоположный — получится третья мнимая единица со знаком «-«. Не напоминает правило векторного перемножения ортов в декартовых координатах? Это оно и есть, то есть мы получаем

Пользуясь этими правилами перемножим два кватерниона

Ого! Не слабо, но мы смело приводим подобные слагаемые

и, ну наверняка вы видите тут до боли знакомые действия над векторами. Пусть у нас будут заданы векторы

тогда каждый кватернион можно представить парой скаляр-вектор

а результат их умножения

Не трудно просто сравнить эту формулу с результатом умножения, которое мы выполнили, при этом считая мнимые единицы ортами декартова базиса. Таким образом, кватернионы включают в себя и векторы трехмерного пространства, и например, кватернионы вида и , будут скалярами, и их произведение эквивалентно произведению скалярных величин

А кватернионы вида и называются векторными кватернионами, и их произведение

дает скалярное, со знаком минус, и векторное произведение составляющих их векторов.

Из-за наличия в результате произведения векторного умножения, операция умножения кватернионов не коммутативна

Ну и надо ли говорить, что обнуляя два последних коэффициента у каждого из кватернионов мы получим произведение комплексных чисел? Думаю не стоит, ибо мы не погружаемся в комплексную область, а если и говорим о комплексных числах, то там где это требуется.

Не стану так же говорить о том, что сложение кватернионов и умножение их на число аналогично соответствующим операциям в комплексной области. А вот о чем надо поговорить, так о сопряжении кватерниона

о связанной с ним операции вычисления нормы

и операции вычисления обратного кватерниона

И ещё одно полезное свойство, касающееся сопряжения произведения кватернионов

Кроме того, норма обратного кватерниона — величина обратная норме исходного

Эти операции имеют непосредственное отношение к тому, для чего в наши дни используют гиперкомплексные числа

2. Кватернион как линейный оператор поворота

Теперь посмотрим на вот такой фокус. Пусть — один кватернион, а — другой кватернион. Докажем небольшую теорему

Преобразование вида не меняет нормы кватерниона .

Проверяется это утверждение прямым вычислением

Действительно, норма кватерниона не изменяет при подобном преобразовании. А если кватернион будет векторным кватернионом, то не изменится норма вектора, которым он определяется. То есть описанное преобразование над вектором, не меняет его длины, оно будет ортогональным, или преобразованием поворота! Дело за малым — выяснить, вокруг какой оси и на какой угол происходит поворот, определяемый конкретным кватернионом. Для этого возьмем (нам ведь никто не мешает так сделать) и представим кватернион в виде

Величину, стоящую в скобках называют вензором (не путать с тензором!) кватерниона. Поупражняемся над его векторной частью

Никто не мешает делать нам эквивалентных преобразований, вот мы и делаем их. Теперь введем замену

На каком основании? Да на том, что сумма квадратов этих величин всегда даст единицу, а если это так, то никто не мешает представить данные величины как синус и косинус некоторого угла. Почему угол делим на два? Нам так хочется, потом это нам пригодится, ведь угол можно взять произвольный. Исходя из введенной замены мы можем переписать кватернион в виде

Заметим, что вектор , введенный нами, является единичным, так как

В довершении позволим себе ещё одно допущение — пусть кватернион будет единичным, то есть

Теперь аккуратно выполним ортогональное преобразование над векторным кватернионом

Теперь умножим результат (2) на обратный кватернион

Для того чтобы не загромождать текст «крокодилами» вычислим отдельно скалярную

и векторную часть

результата преобразования. В конечном итоге, на основании формул (3) и (4), проведя не сложные тригонометрические упрощения, приходим к выводу, что на выходе получается некоторый вектор

Так это же… формула конечного поворота Родрига! Выходит, что преобразование

которое, с учетом того, что для единичного кватерниона операция вычисления обратного кватерниона эквивалентна сопряжению, можно переписать в виде

эквивалентно повороту вектора вокруг оси, задаваемой ортом на угол . Угол поворота и вектор, вокруг которого происходит вращение можно рассчитать по компонентам кватерниона, исходя из замен, введенных нами выше.

Выводы

Мы убедились, что единичный кватернион, компоненты которого построены по формулам

определяет конечный поворот. Четыре параметра, которые мы привели и есть те самые параметры Родрига-Гамильтона, которые однозначно определяют ориентацию твердого тела в пространстве и не вырождаются при любых параметрах вращения. Например, если мы обнулим угол поворота, то орт оси вращения так же станет равен нулю. При повороте на любой конечный угол мы всегда можем рассчитать положение оси поворота.

Что же, а за окном тем временем рассвело… План данной статьи был несколько иным, и мы ни слова не сказали о тензорах. Да оно и к лучшему, зато мы теперь имеем четкое представление о том, что за хитрые параметры ориентации будем использовать в дальнейшем.