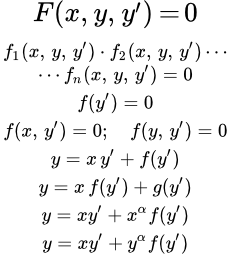Укажите дифференциальные уравнения не разрешенные относительно производной

Дифференциальные уравнения первого порядка, не разрешенные относительно производной

Дифференциальные уравнения, которые удается разрешить относительно производной

Сначала нужно проверить, не удастся ли уравнение решить относительно производной. Если уравнение удается разрешить относительно производной, то оно сводится к одному из ранее рассмотренных типов.

Пример

Решить уравнение:
(1)

Решим это уравнение относительно производной. Возводим уравнение (1) в квадрат:
.
Или:
;
.
Поскольку , то 1″ style=»width:57px;height:20px;vertical-align:-11px;background-position:-362px -390px»> .
Извлекаем квадратный корень. Получаем два значения:
(2) .
Из уравнения (1) следует, что 0″ style=»width:62px;height:20px;vertical-align:-10px;background-position:-300px -390px»> .
Поэтому при 1″ style=»width:46px;height:14px;vertical-align:-7px;background-position:-452px -0px»> , 0″ style=»width:51px;height:20px;vertical-align:-10px;background-position:-446px -247px»> . В уравнении (2) выбираем верхний знак “+”.
При , . В уравнении (2) выбираем нижний знак “–”.

Интегрируем, применяя таблицу интегралов:
(3) .
Поскольку верхний знак “+” относится к 1″ style=»width:46px;height:14px;vertical-align:-7px;background-position:-452px -0px»> , а нижний знак “–” относится к , то
.
Тогда
.

Теперь объясним, как мы вынесли за знак логарифма в (3).
Применим формулу:
.
Приравняем модули левой и правой частей:
.
Подставим ; :
;
;
;
.
Логарифмируем, применяя свойства логарифмов:
.
Отсюда
.

Дифференциальные уравнения, допускающие разложение на множители

Также нужно проверить, не удастся ли представить уравнение в виде произведения множителей:
.
Если такое разложение возможно, то последовательно решают уравнения, составленные из сомножителей:
;
;
;
.
.

Виды не разрешенных уравнений, допускающих решение

Далее приведены виды не разрешенных относительно производной дифференциальных уравнений первого порядка, допускающих решение.

Уравнения, не содержащие x и y

Это уравнения, которые не содержат в явном виде независимую и зависимую переменные:
.
См. Уравнения, содержащие только производную.

Уравнения, не содержащие x или y

Это уравнения, которые не содержат в явном виде либо независимую переменную , либо зависимую переменную :
; или .
См. Уравнения, не содержащие одну из переменных в явном виде.

Дифференциальные уравнения 1-го порядка,
не разрешенные относительно производной

Уравнения 1-го порядка n-ой степени относительно производной

Пусть имеем дифференциальное уравнение

Решаем это уравнение относительно . Пусть

— вещественные решения уравнения (1).

Общий интеграл уравнения (1) выразится совокупностью интегралов:

где есть интеграл уравнения .

Таким образом, через каждую точку области, в которой принимает вещественные значения, проходит интегральных линий.

Пример 1. Решить уравнение .

Решение. Разрешим это уравнение относительно :

Пример 2. Решить уравнение .

Решение. Разрешим уравнение относительно переменной :

Положим , где — параметр; тогда получим Дифференцируя, найдем . Но так как , то будем иметь

Рассмотрим два случая:

1) , откуда , где — произвольная постоянная. Подставляя значение , получаем общее решение данного уравнения:

В равенстве нельзя заменить на и интегрировать полученное уравнение (так как при этом появится вторая произвольная постоянная, чего не может быть, поскольку рассматриваемое дифференциальное уравнение является уравнением первого порядка).

2) , откуда . Подставляя, получим еще одно решение .

Проверим, нарушится ли свойство единственности в каждой точке решения , т.е. является ли оно особым (см. часть 1.11). Для этого возьмем на интегральной кривой произвольную точку , где . Будем теперь искать решение, которое содержится в общем решении и график которого проходит через точку . Подставляя координаты этой точки в общее решение , будем иметь

откуда . Это значение постоянной подставим в . Тогда получим частное решение

которое не совпадает с решением . Для этих решений имеем соответственно . При обе производные совпадают. Следовательно, в точке нарушается свойство единственности, т. е. через эту точку проходят две интегральные кривые с одной и той же касательной. Так как произвольно, то единственность нарушается в каждой точке решения , а это означает, что оно является особым.

2°. Уравнения вида f(y,y’)=0 и f(x,y’)=0

Если уравнения и легко разрешимы относительно , то, разрешая их, получим уравнения с разделяющимися переменными. Рассмотрим случаи, когда эти уравнения не разрешимы относительно .

А. Уравнение вида разрешимо относительно :

Полагаем , тогда . Дифференцируя это уравнение и заменяя на , получим

Получаем общее решение уравнения в параметрической форме

Пример 3. Решить уравнение , где — постоянные.

Решение. Положим , тогда , или . Отсюда и .

Общим решением будет .

Б. Если уравнение вида неразрешимо (или трудно разрешимо) как относительно , так и относительно , но допускает выражение и через некоторый параметр :

то поступаем следующим образом. Имеем . С другой стороны, , так что и ; отсюда

Таким образом, получаем общее решение данного дифференциального уравнения в параметрической форме

Пример 4. Решить уравнение .

Решение. Полагаем , тогда имеем

Отсюда , общее решение .

В. Уравнение вида . Пусть это уравнение разрешимо относительно , то есть .

Полагая , получим . Но и, следовательно, , так что

Таким образом — общее решение уравнения в параметрической форме ( — параметр).

Замечание. В формулах нельзя рассматривать как производную. В них является просто параметром.

Пример 5. Решить уравнение .

Решение. Положим , тогда

Итак, — общее решение.

Аналогично случаю Б можно пытаться решать уравнение методом введения параметра .

3°. Уравнения Лагранжа

Уравнение Лагранжа имеет вид

Полагая , дифференцируя по и заменяя на , приводим это уравнение к линейному относительно как функции . Находя решение этого последнего уравнения , получаем общее решение исходного уравнения в параметрической форме:

Кроме того, уравнение Лагранжа может иметь еще особые решения вида , где — корень уравнения .

Пример 6. Проинтегрировать уравнение .

Решение. Полагаем , тогда . Дифференцируя, находим

Получили уравнение первого порядка, линейное относительно ; решая его, находим

Подставляя найденное значение в выражение для , получим окончательно

Уравнения Клеро

Уравнение Клеро имеет вид .

Метод решения тот же, что и для уравнения Лагранжа. Общее решение уравнения Клеро имеет вид

Уравнение Клеро может иметь еще особое решение, которое получается исключением из уравнений .

Пример 7. Проинтегрировать уравнение .

Решение. Полагая , получаем . Дифференцируя последнее уравнение и заменяя на , найдем

Приравнивая нулю первый множитель, получаем , откуда и общее решение исходного уравнения есть , однопараметрическое семейство прямых. Приравнивая нулю второй множитель, будем иметь . Исключая из этого уравнения и из уравнения , получим — это тоже решение нашего уравнения (особое решение).

С геометрической точки зрения кривая есть огибающая семейства прямых, даваемых общим решением (рис. 14).

Дифференциальные уравнения, не разрешенные относительно производной.

Дифференциальные уравнения, не разрешенные относительно производной.

F(x,y,y’)=0

1. Из уравнения F(x,y,y’)=0 выразить y’ через x и y. Получится одно или несколько уравнений вида y’=f(x,y), каждое из которых надо решить.

Пример.

у’ 2 -y 2 =0

y’=y и y’=-y

dy/y=dx и dy/y=-dx

ln|y|=x+lnC и ln|y|=-xlnD

y=Ce x и y=De -x

2. Метод параметра (простейший вариант метода).

Пусть уравнение F(x,y,y’)=0 можно разрешить относительно y.

y=f(x,y’).

Введем параметр p=y’=dy/dx

Тогда y=f(x,p)

Возьмем полный дифференциал от обеих частей, заменив dy через pdx, получим

Если решение этого уравнения найдено в виде x=φ(p), то получим решение исходного уравнения в параметрической форме:

Пример

y=ln(1+y’ 2 )

p=y’=dy/dx, y=ln(1+p 2 )

При делении на р потеряли решение у=0

3. Если уравнение F(x,y,y’)=0 можно разрешить относительно х:

x=f(y,y’), то также как в 2 вводим параметр p=y’=dy/dx

4. Уравнение Лагранжа

y=xφy’+Ψ(y’)

и уравнение Клеро

y=xy’+Ψ(y’)

являются частными случаями, рассмотренными в пункте 2.

5) Немного об особых решениях. Решение y=φ(х) уравнения F(x,y,y’)=0 называется особым, если через каждую его точку, кроме этого решения, проходит и другое ршение, имеющее в этой точке ту же касательную, что и решение φ(х), но не совпадающее сним в сколь угодно малой окрестности этой точки. Пусть F(x,y,y’), δF/δy и δF/δy’ непрерывны. Тогда любое особое решение уравнения F(x,y,y’)=0 удовлетворяет и уравнению δF(x,y,y’)/δy’=0.

Чтобы отыскать особые решения, надо из системы

исключить y‘. Полученное уравнение называется дискриминантной кривой. Для каждой ветви дискриминантной кривой надо проверить, является ли эта ветвь решением и если является, то будет ли оно особым (т.е. нарушается ли единственность в каждой его точке).

Пример.

y=xy’-y 2 — Уравнение Клеро

p=y’=dy/dx, y=xp-p 2

pdx=pdx+xdp-2pdp

(x-2p)dp=0

dp=0, p=c, следовательно

x=2p, y=xp-p 2

y=Cx-C 2 или y=(x 2 /2)-(x 2 /4)

y=x 2 /4-особое решение

y=x 2 /4 решение исходного уравнения. Докажем, что особое.

Берем произвольную точку на решении y=x 2 /4, например (x_o,x 2 _o/4). найдем С, при котором прямая y=Cx-C 2 также проходила через эту точку x 2 _o/4=Cx_o-C 2 , следовательно C=x_o/2, т.е. y=(x_o/2)x-(x 2 _o/4).