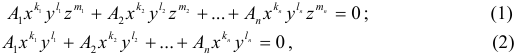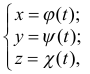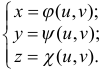Укажите какие уравнения определяют алгебраические поверхности

Алгебраические линии и поверхности

Общее понятие об уравнениях

Алгебраической поверхностью (линией) называется множество, которое в какой-нибудь декартовой системе координат может быть задано уравнениями поверхности (1) и линии (2):

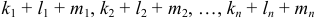
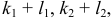
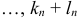
где все показатели степени — целые неотрицательные числа, а наибольшая из сумм для поверхности и для линии называется степенью уравнения, или порядком поверхности (линии).

Всякая неалгебраическая линия (поверхность) называется трансцендентной.

Теорема. Если поверхность (линия) в некоторой декартовой системе координат может быть задана уравнением вида (1) или (2), то и в любой другой декартовой системе координат она может быть задана уравнением того же вида, имеющим ту же степень. То есть порядок алгебраической линии (поверхности) является инвариантным.

Инвариантом называется всякая величина, не меняющаяся при изменении системы координат.

Представим себе, что линия — это траектория движущейся точки. В каждый момент времени нам известно положение точки, т.е. ее координаты относительно выбранной заранее системы координат. Тогда мы приходим к параметрическим уравнениям линии

где — параметр.

По аналогии параметрические уравнения поверхности имеют вид

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Алгебраические уравнения поверхностей

Напомним, что многочленом степени одной переменной называется выражение вида

где — действительные числа (коэффициенты многочлена), — старший коэффициент, — свободный член. Степень многочлена обозначается .

Многочленом трех переменных называется выражение вида

называется степенью многочлена трёх переменных.

Алгебраической поверхностью называется множество точек, которое в какой-либо аффинной системе координат может быть задано уравнением вида

где — многочлен трех переменных .

Уравнение вида (4.11) называется алгебраическим уравнением с тремя неизвестными. Степенью уравнения (4.11) называется степень многочлена . Одна и та же поверхность может быть задана уравнением вида (4.11) с многочленами разных степеней. Порядком алгебраической поверхности называется наименьшая из степеней этих многочленов.

Всякую неалгебраическую поверхность называют трансцендентной.

В примере 4.1,а,б,в,г — поверхности алгебраические: а — первого порядка. б,в,г — второго порядка. Примером трансцендентной поверхности служит цилиндрическая поверхность (см. рисунок), образующие которой, параллельные оси , пересекают координатную плоскость в точках синусоиды . Эту линию нельзя задать уравнением вида (4.11).

Теорема (4.1) об инвариантности порядка алгебраической поверхности

Если в некоторой аффинной системе координат в пространстве поверхность задана уравнением (4.11), то и в любой другой аффинной системе координат эта поверхность задается уравнением того же вида (4.11) и той же степени. Другими словами, порядок алгебраической поверхности является инвариантом (остается неизменным в любой аффинной системе координат).

Теорема доказывается аналогично теореме 3.1.

В аналитической геометрии в пространстве изучаются:

– алгебраические поверхности первого порядка , описываемые алгебраическим уравнением первой степени с тремя неизвестными

– алгебраические поверхности второго порядка , описываемые алгебраическим уравнением второй степени с тремя неизвестными

1. Теорема 4.1 фактически выражает свойство многочленов: при линейной невырожденной замене переменных

где , степень многочлена не изменяется.

2. Алгебраическое уравнение (4.11) может не иметь действительных решений. Например, в пространстве нет точек, координаты которых удовлетворяют уравнению . Однако в области комплексных чисел, согласно основной теореме алгебры, любое алгебраическое уравнение имеет решения. Поэтому каждое алгебраическое уравнение (4.11) вида , где задает некоторую алгебраическую поверхность в трехмерном комплексном пространстве (см. пункт 2 замечаний 2.9). Если все точки этой поверхности вещественные (действительные), т.е. а то поверхность называют вещественной (действительной). В противном случае поверхность называют мнимой.

3. Алгебраическими неравенствами с тремя неизвестными называются неравенства вида

где — многочлен трех переменных . Степенью алгебраического неравенства называется степень многочлена .

4. Многочлены первой степени и алгебраические уравнения (неравенства) первой степени называются линейными.

5. Многочлен второй степени

называется также квадратичной функцией трех переменных; многочлен

называется квадратичной формой (квадратичной частью функции), многочлен — линейной формой (линейной частью функции), коэффициент — свободным членом. По сравнению со стандартной записью многочлена некоторые коэффициенты квадратичной функции удвоены для удобства выполнения алгебраических преобразований.

6. Квадратичную функцию (см. пункт 5) можно записать:

а) в матричном виде

где — матрица квадратичной функции; — расширенный (дополненный единицей) столбец переменных;

б) выделяя квадратичную и линейную части:

где — матрица квадратичной формы, — столбец коэффициентов линейной формы, — столбец переменных.

Матрицы и называются также матрицами малой и большой квадратичных форм квадратичной функции .

7. Многочлены второй степени и алгебраические уравнения (неравенства) второй степени называются квадратичными (квадратными).

8. Теорема 4.1, разумеется, справедлива для прямоугольных систем координат на плоскости. Напомним, что преобразования прямоугольных систем координат являются ортогональными (см. пункт 5 замечаний 2.3). Поэтому соответствующие этим преобразованиям линейные замены переменных (см. пункт 1) с ортогональной матрицей называются ортогональными (неоднородными при или однородными при ). Далее, как правило, будут рассматриваться уравнения, записанные в прямоугольной системе координат .

Уравнения и основные понятия

Определения.

Пусть в пространстве задана декартова прямоугольная система координат. Рассмотрим сферу радиуса \(r\), центр которой находится в точке \(P\) с координатами \((a, b, c)\). Сфера — множество всех точек, отстоящих от центра на одно и то же расстояние \(r\). Обозначим через \((x, y, z)\) координаты некоторой точки \(M\) и выразим через них равенство \(|\overrightarrow|=r\):
$$
\sqrt<(x-a)^<2>+(y-b)^<2>+(z-c)^<2>>=r.\label
$$
Возводя в квадрат обе части равенства, мы придадим ему более удобную форму
$$
(x-a)^<2>+(y-b)^<2>+(z-c)^<2>=r^<2>.\label
$$
Очевидно, что это равенство выполнено для всех точек сферы и только для них. Следовательно, его можно рассматривать как запись определения сферы при помощи координат. Равенство \eqref называется уравнением сферы в рассматриваемой системе координат.

Приведем пример из геометрии на плоскости. Графиком функции \(f\) называется линия \(L\), состоящая из точек, координаты которых связаны соотношением \(y=f(x)\). Если нас интересует в первую очередь линия, а не функция, то можно считать, что соотношение \(y=f(x)\) есть уравнение линии \(L\).

Вообще, под уравнением множества \(S\) в некоторой системе координат следует понимать выражение определения множества \(S\) через координаты его точек, то есть высказывание, верное для координат всех точек множества и неверное для координат точек, ему не принадлежащих.

Часто уравнению множества точек в планиметрии можно придать вид \(F(x, y)=0\), а в стереометрии — вид \(F(x,y,z)=0\), где \(F\) — функция соответственно двух или трех переменных. Уравнение сферы \eqref имеет такой вид, если мы перенесём член \(r^<2>\) в левую часть равенства.

Может случиться, что уравнение какого-либо множества удобнее записать в виде неравенства. Например, шар, ограниченный сферой с уравнением \eqref, имеет уравнение
$$
(x-a)^<2>+(y-b)^<2>+(z-c)^ <2>\leq r^<2>.\nonumber
$$
Однако напрасно было бы надеяться разделить множества на такие, которые задаются равенствами, и такие, которые задаются неравенствами. Действительно, равенство
$$
\Phi(x, y, z)=F(x,y,z)-|F(x, y , z)|=0\nonumber
$$
задает то же множество, что и неравенство \(F(x,y,z) \geq 0\).

Следует подчеркнуть зависимость уравнения от системы координат. При изменении системы координат меняются координаты точки, а потому уравнения одного и того же множества в разных системах координат, вообще говоря, различны.

Приведем несколько утверждений касательно свойств уравнений множеств.

• Если \(P_\) и \(P_\) — уравнения множеств \(S\) и \(T\), то уравнение пересечения \(S \cap T\) есть высказывание, состоящее в том, что \(P_\) и \(P_\) верны одновременно. Такое высказывание обозначается \(P_ \wedge P_\). В случае, когда \(P_\) и \(P_\) — равенства, содержащие координаты точки, \(F_(x, y, z)=0\) и \(F_(x, y, z)=0\), уравнение пересечения есть система уравнений
  $$
  F_(x, y, z)=0, F_(x, y, z)=0.\nonumber
  $$
• Если \(P_\) и \(P_\) — уравнения множеств \(S\) и \(T\), то уравнение объединения \(S \cup T\) — высказывание, состоящее в том, что из \(P_\) и \(P_\) верно хотя бы одно. Такое высказывание обозначается \(P_ \vee P_\).
• В случае, когда \(P_\) и \(P_\) — равенства, содержащие координаты точки, \(F_(x, y, z)=0\) и \(F_(x, y, z)=0\), уравнение объединения можно написать в виде
  $$
  F_(x, y, z) F_(x, y, z)=0.\nonumber
  $$
• Если \(P_\) и \(P_\) — уравнения множеств \(S\) и \(T\), и \(S\) есть подмножество \(T\), то из \(P_\) следует \(P_\).
• Множества \(S\) и \(T\) совпадают тогда и только тогда, когда их уравнения эквивалентны, то есть из \(P_\) следует \(P_\), а из \(P_\) следует \(P_\).

Проиллюстрируем два последних утверждения. Уравнения \eqref и \eqref эквивалентны. Переходя от \eqref к \eqref, мы можем не ставить двойного знака перед корнем, так как \(r \geq 0\). Наоборот, уравнение
$$
z-c=\sqrt-(x-a)^<2>-(y-b)^<2>>\label
$$
не эквивалентно уравнению \eqref. Действительно, хотя возведением в квадрат можно получить \eqref из \eqref, при извлечении корня из \eqref мы получаем
$$
z-c=\pm\sqrt-(x-a)^<2>-(y-b)^<2>>.\nonumber
$$
Это означает, что равенство \eqref выполнено не только для точек, удовлетворяющих \eqref, но и для точек, удовлетворяющих уравнению
$$
z-c=-\sqrt-(x-a)^<2>-(y-b)^<2>>.\label
$$
Уравнение \eqref следует также и из \eqref. Таким образом, уравнения \eqref и \eqref определяют части сферы — “верхнюю” и “нижнюю” полусферы.

Иногда два последних утверждения считают определениями отношений “следует” и “эквивалентно” для уравнений.

Алгебраические линии и поверхности.

Определения алгебраической поверхности и линии.

Алгебраической поверхностью называется множество точек, которое в какой-нибудь декартовой системе координат может быть задано уравнением вида
$$
A_<1>x^>y^>z^>+…+A_x^>y^>z^>=0,\label
$$
где все показатели степени — целые неотрицательные числа. Наибольшая из сумм \(k_<1>+l_<1>+m_<1>, …, k_+l_+m_\) называется степенью уравнения, а также порядком алгебраической поверхности.

Это определение означает, в частности, что сфера, уравнение которой в декартовой прямоугольной системе координат имеет вид \eqref, является алгебраической поверхностью второго порядка.

Алгебраической линией на плоскости называется множество точек плоскости, которое в какой-нибудь декартовой системе координат может быть задано уравнением вида
$$
A_<1>x^>y^>+…+A_x^>y^>=0,\label
$$
где все показатели степени — целые неотрицательные числа. Наибольшая из сумм \(k_<1>+l_<1>, …, k_+l_\) называется степенью уравнения, а также порядком алгебраической линии.

Совсем не обязательно, что алгебраическая поверхность является поверхностью в привычном нам смысле. Например, уравнению \(x^<2>+y^<2>+z^<2>+1=0\) не удовлетворяют координаты ни одной точки, уравнение
$$
(x^<2>+y^<2>+z^<2>)[(x-1)^<2>+(y-1)^<2>+(z-1)^<2>]=0\nonumber
$$
определяет две точки, уравнение \(y^<2>+z^<2>=0\) определяет линию (ось абсцисс). Такое же замечание надо сделать и об алгебраических линиях.

Теоремы о порядке алгебраических линий и поверхностях в различных декартовых системах координат.

Приведенные определения имеют существенный недостаток. Именно, не известно, какой вид имеет уравнение поверхности в какой-нибудь другой декартовой системе координат. Если же уравнение и имеет в другой системе координат уравнение вида \eqref, то порядок какого из этих уравнений мы будем называть порядком поверхности? Те же вопросы возникают и об алгебраических линиях. Ответом служат следующие теоремы, которые имеют одинаковые доказательства (будем доказывать вторую теорему).

Алгебраическая поверхность порядка \(p\) в любой декартовой системе координат может быть задана уравнением вида \eqref порядка \(p\).

Алгебраическая линия порядка \(p\) на плоскости в любой декартовой системе координат может быть задана уравнением вида \eqref порядка \(p\).

Для доказательства перейдем от системы координат \(O, \boldsymbol_<1>, \boldsymbol_<2>\), о которой шла речь в определении, к произвольной новой системе координат \(O’, \boldsymbol’_<1>, \boldsymbol’_<2>\). Старые координаты \(x, y\) связаны с новыми координатами \(x’, y’\) формулами:
$$
x=a_<1>^<1>x’+a_<2>^<1>y’+a_<0>^<1>,\\ y=a_<1>^<2>x’+a_<2>^<2>y’+a_<0>^<2>.\label
$$

Чтобы получить уравнение линии в новой системе координат, подставим в ее уравнение \(F(x, y)=0\) выражения \(x\) и \(y\) через \(x’\) и \(y’\). При умножении многочленов их степени складываются. Поэтому \((a_<1>^<1>x’+a_<2>^<1>y’+a_<0>^<1>)^\) — многочлен степени \(k\) относительно \(x’\) и \(y’\), а \((a_<1>^<2>x’+a_<2>^<2>y’+a_<0>^<2>)^\) — многочлен степени \(l\). Таким образом, каждый одночлен вида \(Ax^y^\) есть многочлен степени \(k+l\) относительно \(x’\) и \(y’\). Степень суммы многочленов не выше максимальной из степеней слагаемых. (Она окажется ниже, если члены с максимальными степенями уничтожатся.)

Итак, мы доказали пока, что алгебраическая линия в любой декартовой системе координат может быть задана уравнением \(G(x’, y’)=0\) вида \eqref, причем степень многочлена \(G(x’, y’)\) не больше степени многочлена \(F(x, y)\), то есть степень уравнения не повышается. Нам осталось доказать, что степень уравнения не может и понизиться, а потому не меняется при переходе к другой системе координат.

Поэтому, если мы подставим в \(G(x’, y’)\) выражения \(x’\) и \(y’\) через \(x\) и \(y\), полученные решением уравнений \eqref, мы получим многочлен \(F(x, y)\). Если бы степень \(G\) была меньше степени \(F\), это означало бы, что при переходе от системы координат \(O’, \boldsymbol’_<1>, \boldsymbol’_<2>, \boldsymbol’_<3>\), к системе \(O, \boldsymbol_<1>, \boldsymbol_<2>, \boldsymbol_<3>\) степень уравнения повысилась, чего, как мы видели, быть не может.

Понятие инварианта и цель курса аналитической геометрии.

Порядок алгебраической линии — первый встретившийся нам пример инварианта. Вообще, инвариантом называют всякую величину, не меняющуюся при изменении системы координат. Только инвариантные комбинации величин (коэффициентов, показателей и так далее), входящих в уравнение линии или поверхности, характеризуют ее геометрические свойства, не зависящие от ее расположения относительно системы координат. Какой геометрический смысл имеет порядок линии, мы увидим в конце главы.

Свойство неизменности порядка не относится к различным уравнениям, которые линия или поверхность могут иметь в одной и той же системе координат. Хотя такие уравнения и эквивалентны, среди них могут быть уравнения различных степеней и даже не получаемые приравниванием многочлена нулю. Действительно, следующие три уравнения задают окружность радиуса 1 в декартовой прямоугольной системе координат:
$$
\sqrt+y^<2>>=1,\ x^<2>+y^<2>-1=0,\ (x^<2>+y^<2>-1)^<2>=0.\nonumber
$$

Принято считать, что эквивалентные уравнения вида \eqref, имеющие разные степени, задают разные алгебраические линии (хотя соответствующие множества точек и совпадают). Например, говорят, что последнее из приведенных выше уравнений задает “сдвоенную окружность”.

Теперь мы можем указать основной предмет курса аналитической геометрии. Это — исследование линий и поверхностей первого и второго порядка, которые доступны для изучения средствами элементарной алгебры.

Однако перед этим полезно рассмотреть некоторые более общие уравнения. Мы будем говорить о линиях и поверхностях. Формулирование их общих определений не входит в нашу задачу. Читатель, который любит, чтобы все было точно определено, может под ними понимать соответственно алгебраическую линию и поверхность, однако все результаты имеют место и в более общем случае.

Уравнения, не содержащие одной из координат.

Рассмотрим частный случай уравнения поверхности \(F(x,y,z)=0\), когда левая часть уравнения не зависит от одной из переменных, например, от \(z\), и уравнение имеет вид \(F(x, y)=0\). Пусть точка \(M_<0>(x_<0>, y_<0>, z_<0>)\) лежит на поверхности. Тогда все точки с координатами \(x_<0>, y_<0>, z\) при любых \(z\) также лежат на поверхности. Легко заметить, что все точки с координатами такого вида заполняют прямую, проходящую через \(M_<0>\) в направлении вектора \(\boldsymbol_<3>\). Таким образом, вместе со всякой точкой \(M_0\) на поверхности лежит прямая, проходящая через \(M_0\) в направлении вектора \(\boldsymbol_<3>\).

Поверхность, которая состоит из прямых линий, параллельных заданному направлению, называется цилиндрической поверхностью или цилиндром, а прямые линии — ее образующими (рис. 5.1). Линию, лежащую на поверхности и пересекающую все образующие, называют направляющей.

Рис. 5.1

Таким образом, мы показали, что уравнение, не содержащее одной из координат, определяет цилиндр с образующими, параллельными соответствующей координатной оси.

В качестве примера рекомендуем читателю нарисовать поверхность, заданную уравнением \(x^<2>+y^<2>=r^<2>\) в декартовой прямоугольной системе координат в пространстве. Эта поверхность — прямой круговой цилиндр. Еще один вопрос, над которым стоит подумать: как выглядят множества, уравнения которых не содержат двух из трех координат, то есть имеют, например, вид \(F(x)=0\)?

Однородные уравнения. Конусы.

Пусть для каждой тройки чисел \((x, y, z)\) из области определения функции \(F(x,y,z)\) и для каждого числа \(\lambda\) тройка чисел \((\lambda x, \lambda y, \lambda z)\) также принадлежит области определения. Кроме того, пусть \(F(\lambda x, \lambda y, \lambda z)=\lambda^ F(x,y,z)\), где \(s\) — натуральное число. Тогда \(F\) называется однородной функцией степени \(s\).

Рассмотрим поверхность, определяемую в некоторой декартовой системе координат уравнением \(F(x,y,z)=0\), где \(F\) — однородная функция. Если точка \(M\) с координатами \((x, y, z)\) принадлежит поверхности, то при любом \(\lambda\) точка \(P(\lambda x, \lambda y, \lambda z)\) также принадлежит поверхности. Радиус-векторы точек \(M\) и \(P\) коллинеарны, и потому точка \(P\) лежит на прямой \(OM\) (рис. 5.2).

Поверхность, которая состоит из прямых линий, проходящих через фиксированную точку, называется конической поверхностъю или конусом. Прямые линии называются ее образующими, а точка — вершиной конуса (рис. 5.2). Линию, лежащую на поверхности, не проходящую через вершину и пересекающую все образующие, называют направляющей.

Рис. 5.2

Мы доказали, что уравнение \(F(x,y,z)=0\), где \(F\) — однородная функция, определяет конус с вершиной в начале координат.