Логарифмические уравнения в задаче C1
18 февраля 2014
В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.
Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.
Замечание по поводу логарифмический уравнений
Перед тем как переходить непосредственно к уравнению, хочу поделиться небольшой исторической справкой. Дело в том, что ЕГЭ по математике в том виде, котором нам предстоит его сдавать, существует в России уже не первый год. И то уравнение, которое вы сейчас видите на своих экранах, появилось в контрольно-измерительных материалах уже давно.
Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения, но при этом не могут понять: с чего им вообще начинать и как подступиться к логарифмам? Такая проблема может возникнуть даже у сильных, хорошо подготовленных учеников.
В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:
А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.
Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются — правила преобразования логарифмических выражений. Зная их, вы без труда разберетесь даже с самыми навороченными уравнениями в ЕГЭ по математике.
И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!
Решение логарифмического уравнения в задаче C1
Итак, решаем уравнение:
В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:
. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c одержали, обязательно нужно привести к уравнению вида:
Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:
- Слева у нас стоит сумма двух чисел, одно из которых вообще не является логарифмом.
- Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.
Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения, к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.
Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.
Сумма логарифмов и логарифм произведения
Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:
log a f ( x ) + log a g ( x ) = log a f ( x ) · g ( x )
Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:
Здесь нужно понимать: когда мы говорим «Любое основание b », то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения, а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:
Давайте посмотрим, что происходит в нашем случае:
Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:
Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания. Переходим к следующему шагу.
Правила вынесения степеней из логарифма
Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:
Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.
С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:
Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/ k .
Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:
Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n ), окажется в числителе. А то, что было степенью у основания, a k , отправится в знаменатель.
И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.
Вынесение степени из основания логарифма
Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:
Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:
Наконец, перепишем исходное уравнение с учетом новых коэффициентов:
log2 2(9 x 2 + 5) = log2 (8 x 4 + 14)
Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.
Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.
Деление дроби на дробь: дополнительные соображения
Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:
Давайте разберемся, что такое дробь. Запишем:
А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:
Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.
Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.
Избавление от знака логарифма
Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:
2(9 x 2 + 5) = 8 x 4 + 14
Давайте раскроем скобки слева. Получим:
18 x 2 + 10 = 8 x 4 + 14
Перенесем все из левой части в правую:
8 x 4 + 14 − 18 x 2 − 10 = 0
Приведем подобные и получим:
8 x 4 − 18 x 2 + 4 = 0
Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:
4 x 4 − 9 x 2 + 2 = 0
Перед нами обычное биквадратное уравнение, и его корни легко считаются через дискриминант. Итак, запишем дискриминант:
D = 81 − 4 · 4 · 2 = 81 − 32 = 49
Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x , а x 2 , потому что у нас биквадратное уравнение. Итак, наши варианты:
Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная. И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.
Теперь расписываем второй корень нашего биквадратного уравнения:
Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:
Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!
Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9 x 2 + 5 (эта функция всегда положительна), либо 8 x 4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.
Прекрасно, теперь переходим ко второй части задачи.
Отбор корней логарифмического уравнения на отрезке
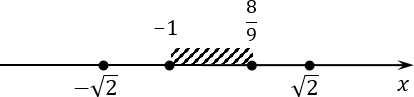
Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:
Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.
Иррациональные корни
Начнем с иррациональных корней. Заметим, что 8/9 x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.
Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:
Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.
Давайте отметим подходящие корни на оси координат:
Окончательным ответом будут два корня: 1/2 и −1/2.
Сравнение иррациональный чисел: универсальный алгоритм
В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:
Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:
Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.
Как это делается? Делаем то же самое, что и с обычными неравенствами:
- Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак. Вот такая галочка V изменилась бы на такую — Λ.
- Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат, чтобы избавится от радикала.
Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.
При решении это оформляется вот таким образом:
Теперь это все легко сравнивается. Дело в том, что 64/81 a или b , именно логарифм, равный другому логарифму.
Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т.д.) мы сведем это уравнение именно к каноническому.
Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:
- Привести все свободные элементы к логарифму;
- Затем эти логарифмы сложить;
- В полученной конструкции все логарифмы привести к одному и тому же основанию.
В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!
Методическая разработка урока по теме «Логарифмические уравнения»
Разделы: Математика
Цели урока:
- Повторение основных приемов преобразования и методов решения логарифмических уравнений; акцентирование внимания учащихся на возможных ошибках в решении логарифмических уравнений.
- Расширение знаний темы “Логарифмические уравнения” посредством знакомства с уравнениями, содержащими знак модуля.
- Развитие познавательных способностей посредством содержания и формы проведения урока, развития вариативного мышления, развития общеучебных навыков, работа с книгой, с компьютером.
- Развитие коммуникативных навыков, развитие монологической речи, умение критически мыслить, отстаивать свою точку зрения.
- Организация на урок /5 минут/.
- Повторение теоретического материала по теме “ Равносильные уравнения. Решение логарифмических уравнений”:
а) устная работа (просмотр презентаций, обсуждение теоретических вопросов) / 7–8 минут/;
б) диктант с последующей проверкой /5–7 минут/. - Работа учащихся с карточками (нахождение ошибок) (самостоятельно), обсуждение решений уравнений /10-12 минут/.
- Совместная работа учащихся и учителя (решение уравнений в тетрадях и у доски) /10 минут/.
- Подготовка к экзаменам:
а) разбор уравнений, решения которых заранее подготовлены учителем для просмотра через плазменный экран и решаемого учеником /15 минут/;
б) самостоятельная работа учащихся (по карточкам разного уровня сложности) /20минут/. - Итог урока, выставление оценок /2 минуты/.
I этап урока — организационный
Учитель сообщает учащимся тему урока, цель и добавляет, что во время урока они будут пользоваться раздаточным материалом, находящимся на партах.
II. Повторение теоретического материала по теме: “ Равносильные уравнения. Решение логарифмических уравнений”
Для того, чтобы решать логарифмические уравнения, следует повторить необходимые для этого теоретические сведения:
Выступление I ученика
Приложение 1 показ слайдов демонстрационной презентации с четкими формулировками:
- слайд №1-определение равносильных уравнений;
- слайд № 2 – определение уравнения следствия;
- слайд № 3 – область допустимых значений уравнения
- слайд №4- что понимают под логарифмическим уравнением;
Диктант (с последующей взаимопроверкой)
Возможные ответы: “+”-да , “-” — нет
| Вариант 1 | Вариант 2 |
| Верно ли утверждение: | Верно ли утверждение: |
| Если 4 х =7, то х=log47 |
Если log525=x, то х=2
Если log381=x, то х=4
lgxlg5=3 и lg(x+5)=3
lg
lgx+lg(x 3 -1)= 2 и lg(x(x 3 -1))=2

Выступление II ученика
Приложение2 показ слайдов демонстрационной презентации с основными видами логарифмических уравнений:
- слайд №1–
;
- слайд №2 –
;
- слайд №3 – в уравнении логарифмы с разными основаниями;
- слайд №4–
;
- слайд №5– метод введения новой переменной.
1. Укажите промежуток, которому принадлежит больший корень уравнения ln(х — 5) 2 = 0.
2. Найдите произведение корней уравнения 1- lg(x 2 +1) = 0.
3. Укажите промежуток, которому принадлежат корни уравнения log0,5(x — 9) = 1 + log0,55.
4. Укажите промежуток, которому принадлежит корень уравнения log4(x — 5) = log255.
Задание 1 2 3 4 Номер ответа 4 2 1 2
III. Работа учащихся с карточками. Объяснение ошибок
Учащимся на отдельных листах предлагаются уравнения с решениями, содержащими ошибки. Необходимо обнаружить эти ошибки, объяснить их и выполнить решение предложенных уравнений правильно (допускается решение уравнения иным способом после обнаружения ошибки в приведенном варианте решения).
Обсуждение решения уравнений
В задаче 1 для преобразования выражения 






В задаче 2 при преобразовании выражения log3 (x + 4) 2 пропущен знак модуля.
В задаче 3 преобразование дроби 
В задаче 4 при преобразовании основания логарифма был поставлен знак модуля, однако, поскольку показатель степеней нечетный, то такое преобразование привело к расширению множества решений (-2 — посторонний корень для исходного уравнения).
В решении задачи 5 нарушено условие монотонности соответствующей функции (если f— монотонная функция и а ЄDf, bЄ Df, то f (a) = f(b) а = b) .
IV. Решение уравнений
Этот этап урока может быть организован различно: учащиеся выполняют самостоятельно решение уравнений с последующей проверкой, кто-то из учащихся показывает решение на доске и пр.
V. Подготовка к экзаменам
а) разбор решения уравнений
Приложение 3) показ слайдов демонстрационной презентации с решениями уравнений:
слайд №1- решение уравнения
слайд № 2- найдите абсциссы всех точек пересечения графиков функций 
слайд № 3- решение уравнения |log2х — 1| = (4 — 8x) (log2x — 1).
б) самостоятельная работа учащихся (каждый из учащихся может сам проверить свой уровень подготовки к ЕГЭ по данной теме. Ученикам предлагается тест, содержащий задания трех уровней сложности).
1. Решите уравнение log3(x+2)=3
2. Укажите промежуток, которому принадлежит корень уравнения log12(x+3)= log12(6-5x)
3. Найдите сумму корней уравнения 

5. Найдите произведение корней уравнения
1.Решите уравнение log11(2x+1)=2
2. Укажите промежуток, которому принадлежит корень уравнения –log5(4-х)= log152-1
3. Найдите сумму корней уравнения
2) 
3) 
4)
4. Напишите целые корни уравнения
Решите уравнение 3
1. Решите уравнение log0,5(2x-0,75)=2
2. Укажите промежуток, которому принадлежит корень уравнения
1) (-4;2); 2) (-2, 0); 3) (0;0,5); 4) (0,5;4)
3. Решите уравнение log3х+14
4. Найдите наибольший корень уравнения log3¦х+2¦+9= log3(х+2) 4
5. Решите уравнение
задания 1 2 3 4 5 Вариант 1 3 1 2 16 1 Вариант 2 3 1 2 49 -2 Вариант 3 4 2 81 25 -1
Проверка выполнения тестов на оценку. Анализ выполнения тестов.
VI. Подведение итогов урока
Учитель еще раз обращает внимание на те типы уравнений и теоретические факты, которые вспоминали на уроке, рекомендует выучить их. Отмечает наиболее успешную работу на уроке отдельных учащихся, при необходимости выставляет отметки. Каждый из учащихся проверил свой уровень подготовки к ЕГЭ по теме “Логарифмические уравнения” и делает для себя соответствующие выводы.
Решите уравнение (1—6).
1. 

3. log2 (x 2 + 10х + 25) = 2.
4.
Урок-презентация «Решение логарифмических уравнений и неравенств»
Урок систематизации знаний и умений учащихся по теме» Решение логарифмических уравнений и неравенств». Цель урока: систематизировать знания учащихся по применению свойств функции при решении задач; продолжить развитие вычислительных навыков и логического мышления; воспитание умения работать в группе, создание положительной мотивации учения.
В ходе урока учащиеся повторят: применение свойств функции при решении уравнений и неравенств; алгоритм проверки корней уравнений.
Просмотр содержимого документа
«Урок-презентация «Решение логарифмических уравнений и неравенств» »
Алгебра 11 класс «Логарифмические уравнения и неравенства»
Урок составила учитель математики
ОСШГ № 2 г. Актобе
Власова Наталья Николаевна
«Чтобы переварить знания, надо поглощать их
- Систематизация знаний и умений учащихся по применению свойств логарифмической функции при решении задач
- Развитие вычислительных навыков и логического мышления
- Воспитание умения работать в группе, создание положительной мотивации учения
- Свойства логарифмов и логарифмической функции, применяемые при решении логарифмических уравнений.
- Проверка полученных корней при решении логарифмических уравнений
- Свойства логарифмической функции применяемые при решении логарифмических неравенств


Контроль знаний и умений учащихся по теме: «Логарифмические уравнения и неравенства» с помощью теста
1.Найдите произведение корней уравнения: log π (x 2 + 0,1) =0
1) — 1,21; 2) — 0,9; 3) 0,81; 4) 1,21.
2. Укажите промежуток, которому принадлежат корни уравнения log 0,5 (x – 9 ) = 1 + log 0,5 5 1) ( 11; 13 ); 2) ( 9; 11 ); 3) ( -12; -10 ); 4) [ -10; -9 ].
3. Укажите промежуток, которому принадлежит корень уравнения log 4 (4 – х ) + log 4 x = 1 1) ( -3; -1 ); 2) ( 0; 2 ); 3) [ 2; 3 ]; 4) [ 4; 8 ].
4. Найдите сумму корней уравнения log √3 x 2 = log √3 ( 9x – 20 ) 1) — 13; 2) — 5; 3) 5; 4) 9.
5. Укажите промежуток, которому принадлежит корень уравнения log 1/3 (2х – 3 ) 5 = 15 1) [ -3; 2 ); 2) [ 2; 5 ); 3) [ 5; 8 ); 4) [ 8; 11 ).

6. . Укажите промежуток, которому принадлежит корень уравнения lg ( х + 7 ) – lg ( х + 5 ) = 1 1) ( -∞; -7 ); 2) ( -7; -5 ); 3) ( -5; -3 ); 4) ( 0; +∞).
7. Решите неравенство log 3 ( 4 – 2х ) = 1 1) ( -∞; 0,5 ]; 2) ( -∞; 2 ]; 3) [ 2; + ∞ ); 4) [ 0,5; + ∞ ).
8. Решите неравенство log π ( 3х + 2 )
9. Решите неравенство log 1/9 ( 6 – 0,3х ) -1 1) ( -10; +∞ ); 2) (-∞; -10 ); 3) ( -10; 20 ); 4) ( -0,1; 20 ).
10. Найдите число целых отрицательных решений неравенства lg ( х + 5 )
1.Найдите произведение корней уравнения: lg (x 2 + 1) = 1 1) — 99; 2) — 9; 3) 33; 4) -33.
2. Укажите промежуток, которому принадлежит корень уравнения log 4 (x – 5 ) = log 25 5 1) ( -4; -2 ); 2) ( 6; 8 ); 3) ( 3; 6 ); 4) [ -8; -6 ].
3. Укажите промежуток, которому принадлежит корень уравнения lоg 0,4 (5 – 2х ) — lоg 0,4 2 = 1 1) ( -∞; -2 ); 2) [ -2; 1 ]; 3) [ 1; 2 ]; 4) ( 2; +∞).
4. Найдите сумму корней уравнения lg (4x – 3 ) = 2 lg x 1) — 2; 2) 4; 3) -4; 4) 2.
5. Укажите промежуток, которому принадлежит корень уравнения log 2 (64х² ) = 6 1) [ 5; 7]; 2) [ 9; 11 ]; 3) ( 3; 5 ); 4) [ 1; 3 ].

6 . . Укажите промежуток, которому принадлежит корень уравнения lоg 2 ( х — 1 )³ = 6 log 2 3 1) [ 0; 5 ); 2) [ 5; 8 ); 3) [ 8; 11 ); 4) [ 11; 14 ).
7. Решите неравенство log 0,8 ( 0,25 – 0,1х ) -1 1) ( -∞; 2,5 ); 2) ( -10; 2,5); 3) ( 2,5; + ∞); 4) ( -10; + ∞).
8. Решите неравенство log 1,25 (0,8х + 0,4 )
9. Решите неравенство log 10/3 ( 1 – 1,4х )
10. Найдите число целых решений нер-ва lоg 0,5 ( х — 2 ) = — 2 1) 5; 2) 4; 3) бесконечно много; 4) ни одного.
http://urok.1sept.ru/articles/565266
http://kopilkaurokov.ru/matematika/presentacii/urok-priezientatsiia-rieshieniie-logharifmichieskikh-uravnienii-i-nieravienstv
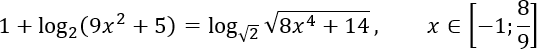
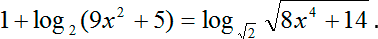
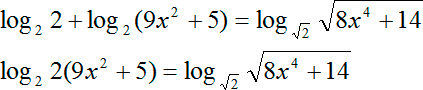
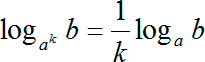
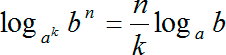
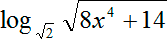
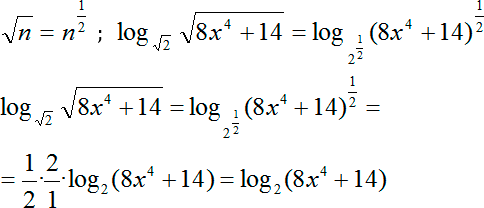
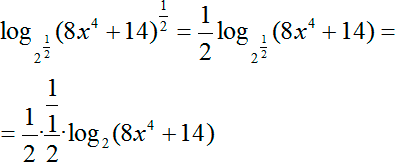
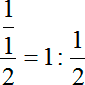
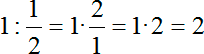
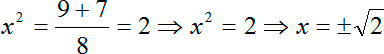


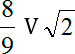
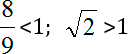
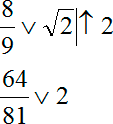

 ;
; ;
; ;
;






















