Умф классификация уравнений в частных производных

Классификация уравнений математической физики (линейных дифференциальных уравнений с частными производными второго порядка)

Многие задачи механики, физики, технологии приводят к исследованию дифференциальных уравнений с частными производными второго порядка, называемых уравнениями математической физики.

Дифференциальные уравнения математической физики,которые мы будем изучать, – это линейные уравнения второго порядка. Как указано ранее уравнение называют линейным, если оно первой степени относительно искомой функции и всех ее производных и не содержит их произведений, то есть если это уравнение может быть записано в виде уравнения (18.1)

Общепринята следующая классификация уравнения (18.1). Принадлежность уравнения к тому или иному типу определяется коэффициентами при старших производных.

Обозначим 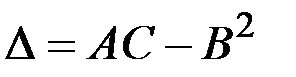– дискриминант уравнения. В зависимости от знака функции Δ уравнение (18.1) относится в данной области к одному из следующих типов:

Δ 0 – эллиптический тип;

Δ не сохраняет постоянного знака – смешанный тип.

Замечание. В уравнении (18.1) независимыми переменными являются координаты x и y. Во многих задачах одной из двух независимых переменных является время и уравнение (18.1) можно записать через x и t (см. табл. 1).

B = C = 0; Δ = 0 – это уравнение параболического типа.

В уравнении Лапласа

–

A = 1, B = 0, C = 1, Δ = AC – B 2 > 0 – это уравнение эллиптического типа.

–

уравнение смешанного типа в любой области P, содержащей точки оси 0X. При y 0 – эллиптического типа, при y = 0 – линии параболичности.

Докажите самостоятельно, что уравнение

– гиперболического типа.

Краевые условия

Дифференциальные уравнения с частными производными имеют в общем случае бесчисленное множество решений. Поэтому, если физический процесс описывается с помощью уравнения с частными производными, то для однозначной характеристики этого процесса необходимы какие то дополнительные условия. Эти дополнительные данные состоят из краевых, то есть граничных и начальных условий.

Граничные условия заключаются в том, что указываются значения неизвестной функции u на концах промежутка изменения координаты (в задаче о линейной теплопроводности это концы стержня, в задачах о колебаниях струны – это концы струны и т.д.).

Условия, относящиеся к начальному моменту времени, называются начальными.

В каком же случае задаются какие краевые условия? Для того, чтобы лучше понять это, следует рассмотреть понятие стационарного и нестационарного процессов.

Нестационарными называются задачи, решение которых зависит не только от пространственных координат (x, y, z), но и от времени t. Эти задачи связаны с процессами, протекающими во времени. Например, это процессы распространения тепла, процессы диффузии, колебательные (волновые) процессы, процессы распространения электрических волн и ряд других.

Основными дифференциальными уравнениями математической физики, описывающими нестационарные процессы, являются уравнение теплопроводности

(18.2)

и волновое уравнение

(18.3)

Уравнение (18.2) является уравнением параболического типа, а уравнение (18.3) – гиперболического. Постановка задач для уравнений этих типов характеризуется наличием как граничных, так и начальных условий.

Начальные условия состоят в задании в момент времени t = 0 значений искомой функции u и ее производной (в гиперболическом случае) или только значений самой функции (в параболическом случае).

Таким образом, для уравнения теплопроводности ставится одно начальное условие (то есть условие при t = 0)

а для волнового уравнения – два:

(0, x, y, z) = ψ(x, y, z). (18.6)

В случае, если процесс протекает в неограниченной области (область называется неограниченной, если хотя бы одна из координат ее точек может быть сколь угодно большой, например бесконечный стержень, бесконечная струна и т.д.), то задаются лишь начальные условия (задача Коши).

В случае, если задача ставится для конечного интервала, то должны быть заданы и начальные и граничные условия. Тогда говорят о смешанной задаче.

Для описания стационарных процессов обычно используют уравнения эллиптического типа. Время t в эти уравнения не входит. Такими оказываются уравнения стационарного температурного поля, электростатического поля и т.д. Для задач такого типа ставятся только граничные условия, то есть указывается поведение неизвестной функции на контуре области (см.таблицу 1).

В рассматриваемых нами задачах математической физики именно физические соображения подсказывают, какие дополнительные условия следует поставить в той или иной задаче, чтобы получить единственное ее решение, отвечающее характеру изучаемого процесса.

Важнейшие линейные дифференциальные уравнения математической физики

Тип	Физический смысл	Одномерное уравнение	Многомерное уравнение	Дополнительные (краевые) условия
Гиперболический	Волны (струны, мембраны, течение жидкости) затухающие волны			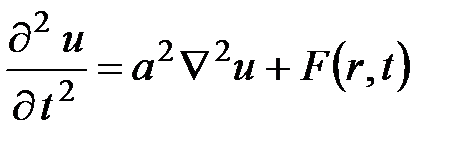Граничные условия; начальные условия для u и
Параболи- ческий	Уравнения теплопроводности, диффузии			Граничные условия; начальное условие для u
Эллиптический	Статический случай			Только граничные условия

– оператор Лапласа.

Классификация дифференциальных уравнений с частными производными.

Для решения многих практических задач необходимо рассматривать так называемые линейные или вполне линейные уравнения в частных производных:

Дифференциальное уравнение с частными производными II порядка с двумя независимыми переменными. A,B,C,D,E.F.G – функции от независимых переменных х и у, имеющие непрерывные частные производные.

Уравнение (1) всегда может быть приведено к одному из трёх стандартных канонических форм:

— если B 2 -4AC 2 -4AC = 0, то уравнение (1) — параболическое;

— если B 2 -4AC > 0, то уравнение (1) – гиперболическое.

К уравнениям с частными производными приводят задачи газодинамики, теплопроводности, процессов переноса в газах, квантовой механики и др.

Полная постановка математической задачи содержит дифференциальное уравнение, а также дополнительные условия, позволяющие выделить единственное решение семейства интегральных поверхностей.

Дополнительные условия называются начальными, если они определяют искомую функцию и её производные в начальный момент времени.

Условия, относящиеся к фиксированным значениям координат, называются краевыми или граничными.

— Граничные условия I рода определяют значения функции на границе области её изменения;

— Граничные условия II рода определяют значения градиента функции на границе области её изменения;

— Граничные условия III рода определяют зависимость функции и её градиента на границе области изменения функции, т.е. в граничных точках пространства записывается дифференциальное уравнение.

Решение дифференциального уравнения с частными производными при заданных начальных условиях называется нестационарной краевой задачей.

Решение дифференциального уравнения с частными производными при заданных граничных условиях называется стационарной краевой задачей.

Пример 1.Исследования стационарных процессов различной физической природы (колебания, теплопроводность, фильтрация и др.) приводят к уравнению эллиптического типа (уравнение Пуассона: ;

Уравнение Лапласа: ).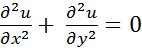

Решение ищется в некоторой области G, на границе этой области Г могут быть заданы краевые условия:

— первого рода —u(x;y)_Г = φ(x;y);

— второго рода — |_г = φ₁(x;y);

— третьего рода — + α₁u = φ₂(x;y); n – нормаль к линии Г.

Пример 2. Примером параболического уравнения может служить уравнение теплопроводности однородного стержня, которое имеет вид:

а 2 – const.

В начальный момент времени t = t₀ для внутренних точек стержня задаётся начальное распределение температуры: u(x;t₀) = φ(x), φ(x) – известная функция. Начальное условие не обеспечивает однозначности решения, т.к. распределение температуры u(x;t) в стержне для последующих моментов времени t > t₀ существенно зависит от того, в каком состоянии находится концы стержня: х=0 и х=l.

Тогда краевые условия запишутся так:

ψ₁(t), ψ₂(t) – известные функции.

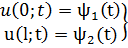
Пример 3.Волновое уравнение для описания колебаний натянутой струны является примером гиперболического уравнения: 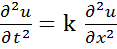, k = const.

В начальный момент времени t = t₀ обычно задаётся форма струны и распределение скорости её точек: u(x;t₀) = φ₁(x), |_г = φ₂(x), φ₁(x), φ₂(x) – известные функции, определённые на 0

Дифференциальные уравнения в частных производных¶

Дифференциальные уравнениями в частных производных с дополнительными уравнениями, выражающими граничные и начальные условия описывают большинство физических процессов. В общем случае линейное дифференциальное уравнение в частных производных второго порядка имеет вид

Классификация проводится в соответствии с характеристическими кривыми второго порядка для данных уравнений. По соотношению значений a, b и c уравнение относят к эллиптическим, параболическим или гиперболическим в данной точке. Тип ДУ определяется знаком выражения, называемого дискриминантом: \(D(x,y) = b^2-4ac\) .

• Если \(D(x, y) , дифференциальное уравнение является эллиптическим в точке (x, y).
• Если \(D(x, y) = 0\) , дифференциальное уравнение является параболическим в точке (x, y).
• Если \(D(x, y) > 0\) , дифференциальное уравнение является гиперболическим в точке (x, y).

Если коэффициенты a, b, c постоянные и значение D не зависит от точки, то в зависимости от знака D уравнение является полностью эллиптическим, гиперболическим или параболическим. В случае если коэффициенты не являются постоянными, для одного и того же уравнения возможны области, в которых оно является уравнением разного типа.

Эллиптические уравнения¶

Эллиптическими уравнениями являются уравнения Лапласа и Пуассона, возникающие в теории потенциала для электрического поля. Так же к уравнению этого тапа сводятся многие стационарные (установившиеся) решения параболических и гиперболических задач.

Простейший вид Эллиптического уравнения:

Такими уравнения описываются стационарное распределение температуры в процессе теплопереноса и стационарное распределение концентрации при диффузии. К уравнению Лапласа приводят и многие другие задачи, например, задача о распределении электростатического поля в однородной непроводящей среде в отсутствие электрических зарядов. В общем случае в векторной форме уравнение Пуассона имеет вид:

где \(u(x, y, z)\) – искомая функция; \(A(x, y, z)\) , \(f(x, y, z)\) – некоторые функции независимых переменных. Функция А описывает «коэффициент распространения» величины u и может являться тензорной величиной в случае анизотропной среды. Функция f это функция источников – скалярная величина, показывающая плотность «скорости появления» величины u в единице объема. В качестве величин, входящих в это уравнение могут использоваться, температура, коэффициент теплопроводности, плотность тепловых источников или потенциал эл. поля, диэлектрическая проницаемость и плотность зарядов и т.д

Параболические уравнения¶

Параболические уравнения появляются в нестационарных задачах теплопроводности, диффузии, иногда параболические задачи получаются из гиперболических уравнений (параболическое приближение в оптике) и т. д. Уравнение теплопроводности, например, имеет вид:

В первом слагаемом коэффициенты это плотность и удельная теплоемкость, во втором слгаемом – коэффициент теплопроводности, правая часть – плотность источников тепла.

Гиперболические уравнения¶

Гиперболические уравнения, часто называют волновыми уравнениями, т.к. с их помощью описывается распространения волн (упругих, электро — магнитных, сдвиговых). К этому же типу уравнений относится уравнение Шредингера квантовой механики.

Начальные и граничные условия¶

Из курса высшей математики известно, что дифференциальные уравнения, как правило, имеют бесконечное множество решений. Это связано с появлением в процессе интегрирования констант, при любых значениях которых решение удовлетворяет исходному уравнению. Решение задач физики связано с нахождением зависимостей от координат и времени определенных физических величин, которые, безусловно, должны удовлетворять требованиям однозначности, конечности и непрерывности. Иными словами, любая задача физики предполагает поиск единственного решения (если оно вообще существует). Поэтому математическая формулировка физической задачи должна помимо основных дифференциальных уравнений, описывающих искомые функции, включать дополнительные уравнения (дифференциальные или алгебраические), описывающие искомые функции на границах рассматриваемой области в любой момент времени и во всех внутренних точках области в начальный момент времени. Эти дополнительные уравнения называют соответственно граничными и начальными условиями задачи. Условия, относящиеся к точкам пространства, называются граничными. Обычно это неизменные условия, накладываемые на значение функции или на ее производную (поток через границу) на границе рассматриваемой области. Начальные условия – условия о значениях физической величины в начальный момент времени. Только после задания обоих типов условий можно получить описание развития процесса во времени. Для ДУЧП редко решают задачи, когда условия внутри области заданы для различных моментов времени, т.к. это сильно усложняет и без того не простую процедуру поиска решения.