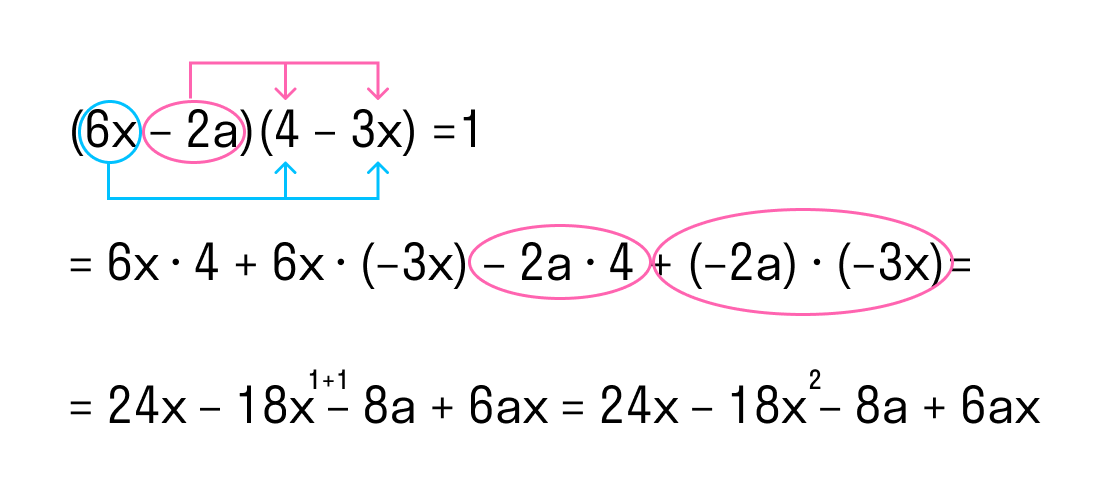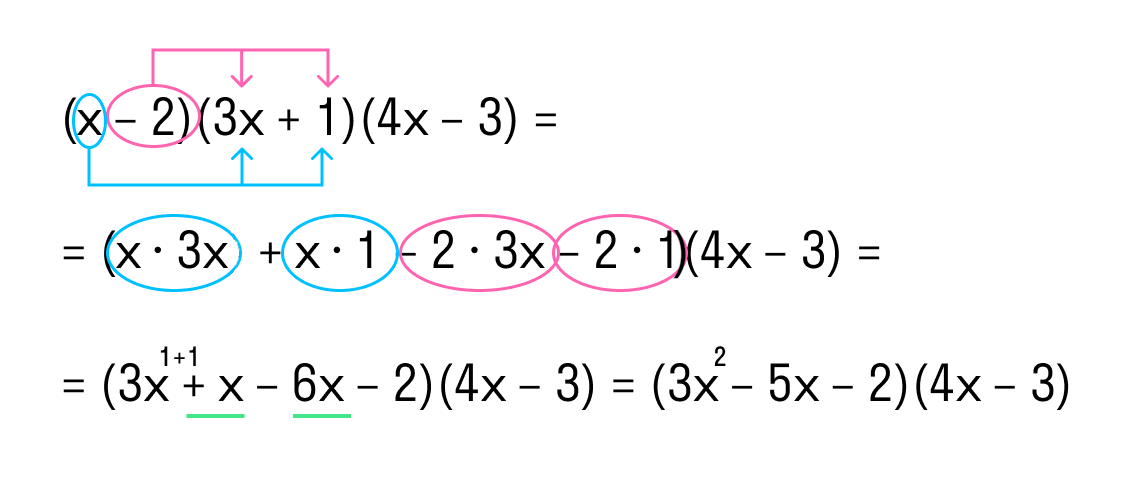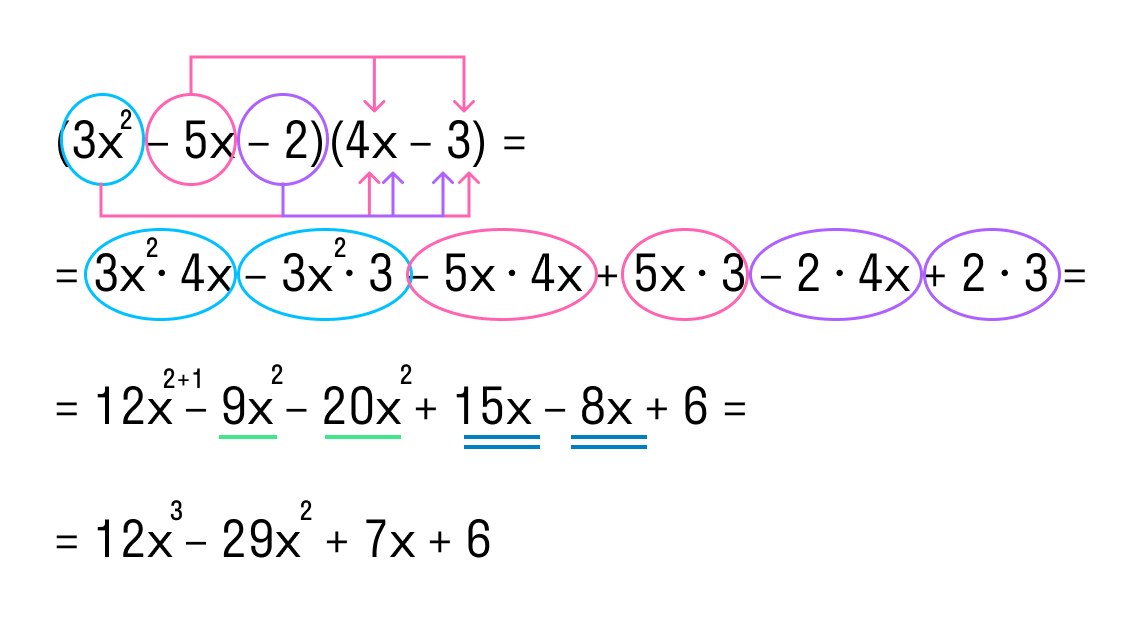Умножение многочлена на многочлен решить уравнение

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Упрощение многочлена.
Умножение многочленов.

С помощью данной математической программы вы можете упростить многочлен.
В процессе работы программа:
— умножает многочлены
— суммирует одночлены (приводит подобные)
— раскрывает скобки
— возводит многочлен в степень

Программа упрощения многочленов не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы вы могли проконтролировать свои знания по математике и/или алгебре.

Данная программа может быть полезна учащимся общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Произведение одночлена и многочлена. Понятие многочлена

Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
\( 5a^4 — 2a^3 + 0,3a^2 — 4,6a + 8 \)
\( xy^3 — 5x^2y + 9x^3 — 7y^2 + 6x + 5y — 2 \)

Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.

Например, многочлен
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 \)
можно упростить.

Представим все слагаемые в виде одночленов стандартного вида:
\( 8b^5 — 2b \cdot 7b^4 + 3b^2 — 8b + 0,25b \cdot (-12)b + 16 = \)
\( = 8b^5 — 14b^5 + 3b^2 -8b -3b^2 + 16 \)

Приведем в полученном многочлене подобные члены:
\( 8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 \)
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных. Такие многочлены называют многочленами стандартного вида.

За степень многочлена стандартного вида принимают наибольшую из степеней его членов. Так, двучлен \( 12a^2b — 7b \) имеет третью степень, а трехчлен \( 2b^2 -7b + 6 \) — вторую.

Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени. Например:
\( 5x — 18x^3 + 1 + x^5 = x^5 — 18x^3 + 5x + 1 \)

Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.

Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:

Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.

Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.

Преобразование (упрощение) произведения одночлена и многочлена

С помощью распределительного свойства умножения можно преобразовать (упростить) в многочлен произведение одночлена и многочлена. Например:
\( 9a^2b(7a^2 — 5ab — 4b^2) = \)
\( = 9a^2b \cdot 7a^2 + 9a^2b \cdot (-5ab) + 9a^2b \cdot (-4b^2) = \)
\( = 63a^4b — 45a^3b^2 — 36a^2b^3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \( (a + b)^2, \; (a — b)^2 \) и \( a^2 — b^2 \), т. е. квадрат суммы, квадрат разности и разность квадратов. Вы заметили, что названия указанных выражений как бы не закончены, так, например, \( (a + b)^2 \) — это, конечно, не просто квадрат суммы, а квадрат суммы а и b. Однако квадрат суммы а и b встречается не так уж часто, как правило, вместо букв а и b в нем оказываются различные, иногда довольно сложные выражения.

Выражения \( (a + b)^2, \; (a — b)^2 \) нетрудно преобразовать (упростить) в многочлены стандартного вида, собственно, вы уже встречались с таким заданием при умножении многочленов:
\( (a + b)^2 = (a + b)(a + b) = a^2 + ab + ba + b^2 = \)
\( = a^2 + 2ab + b^2 \)

Полученные тождества полезно запомнить и применять без промежуточных выкладок. Помогают этому краткие словесные формулировки.

\( (a + b)^2 = a^2 + b^2 + 2ab \) — квадрат суммы равен сумме квадратов и удвоенного произведения.

\( (a — b)^2 = a^2 + b^2 — 2ab \) — квадрат разности равен сумме квадратов без удвоенного произведения.

\( a^2 — b^2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Умножение многочлена на многочлен

О чем эта статья:

Определение многочлена

Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.

Одночлен — это произведение чисел, переменных и степеней.

Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.

Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.

Как привести многочлен к стандартному виду:

1. Привести к стандартному виду все одночлены, которые входят в многочлен.
2. Привести подобные члены.

Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:

Правило умножения двучленов:

(a + b) * (c + d) = ac + ad + bc + bd.

Правило умножения двучлена на трехчлен:

(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.

Правило перемножения трехчленов:

(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc.

Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.

Правило умножения многочлена на многочлен

Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:

• Возьмем два многочлена (a + b) и (c + d) и выполним их умножение.
• Сначала составим их произведение: (a + b)(c + d).
• Теперь обозначим (c + d) как x. После этой замены произведение примет вид: (a + b)x.
• Выполним умножение многочлена на одночлен: (a + b)x = ax + bx.
• Проведем обратную замену x на (c + d):
  a(c + d) + b(c + d). Преобразуем: ac + ad + bc + bd.
• Как изменилось произведение исходных многочленов:
  (a + b)(c + d) = ac + ad + bc + bd.
  Как раз так и выглядит формула умножения многочлена на многочлен.

Правило умножения многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.

Алгоритм умножения многочлена на многочлен:

1. Первый член первого многочлена умножить на каждый член второго многочлена. Второй член первого многочлена умножить на каждый член второго многочлена. И так далее.
2. Сложить полученные произведения.
3. Преобразовать полученную сумму в многочлен стандартного вида.

Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).

• Умножим последовательно первый одночлен 6x из первой скобки на оба одночлена второй скобки.
• Уумножим второй одночлен −2a первой скобки на оба одночлена второй скобки.

Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x 2 – 8a + 6ax.

Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).

• Умножим первый многочлен на второй. Результат запишем в скобках.
  
• Перемножим получившийся многочлен и третий многочлен. Приведем подобные одночлены.
  

Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x 3 – 29x 2 + 7x + 6.

Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры умножения многочлена на многочлен

Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.

Пример 1. Выполнить умножение многочленов:
2 − 3x и x 2 − 7x + 1.

Запишем произведение: (2 − 3x)(x 2 − 7x + 1).

Составим сумму произведений каждого члена многочлена (2 − 3x) на каждый член многочлена (x 2 − 7x + 1). Для этого первый член первого многочлена «2» умножим на каждый член второго многочлена: 2x 2 , 2(−7x) и 2*1.

Теперь второй член первого многочлена «−3x» умножим на каждый член второго многочлена: −3xx 2 , −3x(−7x) и −3x*1.

Из полученных выражений составим сумму: 2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1.

Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.

Осталось полученную сумму преобразовать в многочлен стандартного вида:

2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1 = 2x 2 − 14 x + 2 − 3x 3 + 21x 2 − 3x = (2x 2 + 21x 2 ) + (−14x − 3x) + 2 − 3x 3 = 23x 2 − 17x + 2 − 3x 3 .

Получается, что (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Ответ: (2 − 3x)(x 2 − 7x + 1) = 23x 2 − 17x + 2 − 3x 3 .

Пример 2. Найти произведение трех многочленов:
x 2 + xy − 1, x + y и 2y − 3.

Запишем их произведение: (x 2 + xy − 1)(x + y)(2y − 3).

Умножим первые два многочлена:

(x 2 + xy − 1)(x + y) = x 2 x + x 2 y + xyx + xyy − 1x − 1y = x 3 + 2x 2 y + xy 2 − x − y.

Таким образом: (x 2 + xy − 1)(x + y)(2y − 3) = (x 3 + 2x 2 y + xy 2 − x − y)(2y − 3).

Снова выполним умножение двух многочленов:

(x 3 + 2x 2 y + xy 2 − x − y)(2y − 3) = x 3 2y + x 3 (−3) + 2x 2 y 2 y + 2x 2 y(−3) + xy 2 2y + xy 2 (−3) − x 2 y − x(−3) − y 2 y − y(−3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Ответ: (x 2 + xy − 1)(x + y)(2y − 3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Правила перемножения многочленов между собой

Что такое многочлен

Начать изучение темы умножения многочленов стоит с разбора основных терминов и их особенностей, которые также пригодятся при делении.

Одночленом называют произведение, компонентами которого являются числа, переменные и степени.

Многочлен является выражением в алгебре, составленным в форме суммы или разности нескольких одночленов.

2 x + 4 x y 2 + x + 2 x y 2

В действительности, многочлен всегда состоит из суммы одночленов. К примеру:

3 x − 5 y − 2 x = 3 x + ( − 5 y ) + ( − 2 x )

В связи с этим, при совершении самостоятельных действий с многочленами учитывают знаки одночленов, которые входят в состав сложного выражения.

Члены многочлена — одночлены, которые входят в состав этого многочлена.

Двучлен — многочлен, состоящий из пары членов.

Трехчлен — многочлен, состоящий из трех членов.

Свободный член многочлена — обычное число без буквенной части, которое входит в состав многочлена.

3 x + 5 y + z + 7 — многочлен, где 7 — свободный член.

В качестве многочленов можно представить любые выражения с числами.

Стандартный вид многочлена является представлением многочлена, как суммы из одночленов стандартного вида, в которой отсутствуют подобные одночлены.

Алгоритм приведения многочлена в стандартный вид:

1. Приведение всех его одночленов в стандартный вид.
2. Приведение подобных членов.

Подобные слагаемые, входящие в состав многочлена, носят название подобных членов многочлена. Под приведением подобных слагаемых, из которых состоит многочлен, понимают приведение подобных членов этого многочлена, обладающих по определению идентичной буквенной составляющей.

В качестве тренировки попробуем привести многочлен к стандартному виду:

2 x + 4 x y 2 + x − x y 2

В первую очередь следует привести подобные члены, роль которых в данном примере отведена 2 х и х , 4 x y 2 и — x y 2 :

2 x + 4 x y 2 + x − x y 2 = 3 x + 3 x y 2

В полученном выражении отсутствуют подобные члены. Таким образом, удалось получить многочлен стандартного вида:

Многочлены характеризуются определенной степенью. Сформулируем алгоритм. В процессе определения степени одночлена выполняют следующие действия:

• приведение многочлена к стандартному виду;
• определение одночлена с большей степенью по сравнению с остальными одночленами.

Ранее был преобразован многочлен из 2 х и х , 4 x y 2 и — x y 2 . В результате получили многочлен стандартного вида 3 x + 3 x y 2 . Первый одночлен обладает степенью 1, а второй — 2. Поэтому данный многочлен называют многочленом второй степени. Данная информация пригодится на уроках алгебры.

Степень многочлена стандартного вида — максимальная из имеющихся степеней одночленов, которые входят в состав данного многочлена.

В некоторых заданиях необходимо сначала привести к стандартному виду одночлены, а затем многочлен, из которых он состоит. К примеру, имеется многочлен:

3 x x 4 + 3 x x 3 − 5 x 2 x 3 − 5 x 2 2 x

На первом этапе следует привести к стандартному виду одночлены:

3 x x 4 + 3 x x 3 − 5 x 2 x 3 − 5 2 2 x = 3 x 5 + 3 x 4 − 5 x 5 – 5 x 3

Полученный многочлен допустимо записать в стандартном виде с помощью приведения его подобных членов в уравнении:

3 x x 4 + 3 x x 3 − 5 x 2 x 3 − 5 2 2 x = 3 x 5 + 3 x 4 − 5 x 5 – 5 x 3 = − 2 x 5 + 3 x 4 − 5 x 3

Требуется привести многочлен к стандартному виду:

3 a b + 4 c c + a b + 3 c 2

На первом шаге приведем второй одночлен к стандартному виду. Получим:

3 a b + 4 c c + a b + 3 c 2 = 3 a b + 4 c 2 + a b + 3 c 2

Затем следует выполнить приведение подобных членов:

3 a b + 4 c 2 + a b + 3 c 2 = 4 a b + 7 c 2

В результате можно записать многочлен в стандартном виде:

Особенности умножения многочлена на многочлен

Существуют принципы, согласно которым выполняют умножение одночленов, двучленов и трехчленов:

1. ( a + b ) × ( c + d ) = a c + a d + b c + b d .
2. ( a + b + c ) × ( x + y ) = a x + b x + c x + a y + b y + c y .
3. ( a + b + c ) 2 = a 2 + b 2 + c 2 + 2 a b + 2 a c + 2 b c .

Умножение многочленов предполагает умножение каждого члена, который входит в состав одного многочлена, на каждый член из членов, принадлежащих второму многочлену. Далее полученные результаты необходимо суммировать и привести полученное выражение к многочлену стандартного вида при наличии такой возможности.

Рассмотрим правило на практическом примере:

Согласно алгоритму, требуется каждый из членов первого многочлена ( х + 3 ) перемножить со всеми членами, входящими в состав второго многочлена. Целесообразно обратиться в процессе вычислений к распределительному закону умножения:

( a + b ) c = a c + b c

Применительно к этой задаче, роль переменной с играет многочлен ( у + 4 ) , который включает в себя пару членов у и 4. Сначала найдем произведение ( х + 3 ) и у, далее умножим ( х + 3 ) на 4. Для исключения ошибок предположим, что член 4 временно отсутствует:

( x + 3 ) ( y + 4 ) = x y + 3 y

Затем найдем произведение ( х + 3 ) и 4. Поступим аналогично с предыдущим расчетом:

Выполним вычисления, продолжая расчеты в начальном выражении:

( x + 3 ) ( y + 4 ) = x y + 3 y + 4 x + 12

Разберем второй способ выполнения умножения многочленов. В процессе попробуем каждый их членов одного многочлена перемножить с другим многочленом полностью, а затем, суммировать полученные выражения:

( x + 3 ) ( y + 4 ) = x ( y + 4 ) + 3 ( y + 4 )

Результат преобразований выглядит, как произведение одночлена и многочлена. Вычислим:

( x + 3 ) ( y + 4 ) = x ( y + 4 ) + 3 ( y + 4 ) = x y + 4 x + 3 y + 12

Результат получился такой же, как в решении задачи первым способом. Отличается лишь порядок, в котором расположены члены.

У арифметической операции умножения многочлена на многочлен имеется геометрический смысл. Представим себе некий прямоугольник с длиной а и шириной b:

Найти площадь этой геометрической фигуры можно путем умножения его сторон:

При увеличении сторон прямоугольника на х и у получим:

После того как стороны достроены, следует выделить цветом полученные прямоугольники:

Далее определим площадь для нового прямоугольника. Целесообразно рассчитать площадь каждого маленького прямоугольника и суммировать полученные результаты:

a b + x b + a y + x y

Данное выражение аналогично расчету площади прямоугольника, когда длину умножают на ширину:

В результате получилось справедливое равенство:

( a + x ) ( b + y ) = a b + x b + a y + x y

Рассмотрим пример, в котором стороны прямоугольника имеют числовые значения. Предположим, что длина геометрической фигуры составляет 6 см, ширина равна 3 см. В дальнейшем увеличим длину прямоугольника на 2 см, а к ширине прибавим 1 см.

После построения дополнительных прямоугольников выделим их цветом для наглядности:

Общая площадь прямоугольника составит:

( 6 + 2 ) ( 3 + 1 ) = 32

6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 32

( 6 + 2 ) ( 3 + 1 ) = 6 × 3 + 2 × 3 + 6 × 1 + 2 × 1 = 18 + 6 + 6 + 2 = 32

Если пересчитать по клеточкам на рисунке, то получим 32 квадратных сантиметра:

Правило и алгоритм умножения многочлена на многочлен

Вывести правило, согласно которому умножают многочлены, можно с помощью наглядного примера. Представим, что необходимо перемножить пару многочленов:

Введем х , чтобы обозначить ( c + d ) . Получим:

Умножим многочлен на одночлен:

( a + b ) x = a x + b x

Заменим обратно х на многочлен и выполним преобразования:

a ( c + d ) + b ( c + d ) = a c + a d + b c + b d

Таким образом, получилась формула, по которой умножают один многочлен на другой многочлен:

( a + b ) ( c + d ) = a c + a d + b c + b d

Заметим, что результатом произведения многочленов в любом случае является многочлен.

При умножении одного многочлена на другой многочлен следует каждый из членов первого многочлена умножить на каждый член второго многочлена, а полученные результаты суммировать.

Стандартный алгоритм умножения многочлена на многочлен:

1. Найти произведения первого многочлена и каждого члена второго многочлена. Перемножить второй член первого многочлена с каждым членом второго многочлена и так далее.
2. Вычислить сумму полученных в результате произведений.
3. Записать сумму, которая получилась в итоге, в виде стандартного многочлена.

Примеры решения задач по алгебре для 7 класса

Умножить многочлен a + b на многочлен c + d.

Дополним многочлены скобками и составим произведение:

Перемножим члены многочленов, согласно правилу:

( a + b ) ( c + d ) = a c + b c + a d + b d

Ответ: a c + b c + a d + b d

Найти произведение многочленов:

( − x − 2 y ) ( x + 2 y 2 )

Перемножим члены многочленов:

( − x − 2 y ) ( x + 2 y 2 ) = − x 2 − 2 x y − 2 x y 2 − 4 y 3

В процессе умножаем многочлен ( − x − 2 y ) на первый член многочлена ( x + 2 y 2 ) , которым является x :

( − x − 2 y ) ( x + 2 y 2 ) = − x 2

После результата знак не ставим и сразу приступаем к следующему умножению (−x − 2y) на второй член многочлена ( x + 2 y 2 ) , которым является 2 y 2 :

( − x − 2 y ) ( x + 2 y 2 ) = − x 2 − 2 x y − 2 x y 2

Далее следует перемножить − 2 y и 2 y 2 , что дает в результате − 4 y 3 . Таким образом:

( − x − 2 y ) ( x + 2 y 2 ) = − x 2 − 2 x y − 2 x y 2 − 4 y 3

Ответ: − x 2 − 2 x y − 2 x y 2 − 4 y 3

Требуется умножить многочлены:

( 4 a 2 + 2 a b − b 2 ) ( 2 a − b )

Найдем произведение каждого члена первого многочлена и каждого члена второго многочлена:

( 4 a 2 + 2 a b − b 2 ) ( 2 a − b ) = 8 a 3 + 4 a 2 b − 2 a b 2 − 4 a 2 b – 2 a b 2 + b 3

Приведем подобные слагаемые:

( 4 a 2 + 2 a b − b 2 ) ( 2 a − b ) = 8 a 3 − 4 a b 2 + b 3

Ответ: 8 a 3 − 4 a b 2 + b 3

Нужно умножить многочлены:

Заметим, что перед скобками находится знак минуса. Он играет роль коэффициента, равного -1. В результате перемножаются три сомножителя:

Воспользуемся сочетательным законом умножения. Согласно этому правилу, выражение, включающееся в себя несколько сомножителей, вычисляется в любом порядке. Применительно к нашей задаче, получим:

− 1 ( a + b ) ( с − d ) = − 1 ( a c + b c − a d − b d )

− 1 ( a + b ) ( с − d ) = − 1 ( a c + b c − a d − b d ) = − a c − b c + a d + b d

− 1 ( a + b ) ( с − d ) = ( − a − b ) ( с − d ) = − a c − b c + a d + b d

Ответ: − a c − b c + a d + b d

Нужно найти произведение многочленов:

x 2 ( x + 5 ) ( x − 3 )

Умножим многочлены ( x + 5 ) и ( x − 3 ) . Далее полученный многочлен умножим на x 2 :

x 2 ( x + 5 ) ( x − 3 ) = x 2 ( x 2 + 5 x – 3 x – 15 ) = x 4 + 5 x 3 – 3 x 3 – 15 x 2 = x 4 + 2 x 3 – 15 x 2