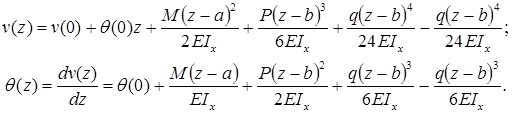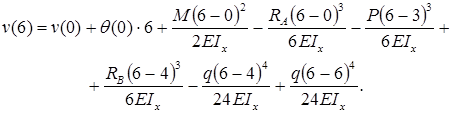Универсальное уравнение упругой линии стержня

Метод начальных параметров. Универсальное уравнение упругой линии балки

В отличие от предыдущего метода в предлагаемом методе начальных параметров (МНП) независимо от количества силовых участков балки приходится находить только две произвольные постоянные интегрирования – прогиб и угол поворота в начале координат (y₀, θ₀). Это достигается путем применения следующих правил при составлении уравнения моментов:

— начало координат выбирается в одном из крайних сечений балки и является общим для всех ее участков;

— внешний сосредоточенный момент М включается в уравнение изгибающих моментов в виде произведения на множитель вида (z – а) 0 , равный единице (здесь а – абсцисса сечения, где действует внешний момент М);

— в случае завершения действия распределенной нагрузки на некотором участке, ее продолжают до конца рассматриваемого участка, а для обеспечения исходного равновесия вводят “компенсирующую” нагрузку обратного направления;

— операции интегрирования или дифференцирования уравнений на всех участках следует выполнять, применяя прием Клебша, т.е. не раскрывая скобок.

С учетом названных правил составляется и решается ДУУЛБ применительно к заданной расчетной схеме балки. Тогда в конечном виде для балки, имеющей большое количество участков с различными внешними нагрузками, общее универсальное уравнение упругой линии балки (УУУЛБ) будет следующим:

После дифференцирования (2.15) получают универсальное уравнение углов поворота балки (УУУПБ)

где y₀, θ₀ – геометрические начальные параметры, т.е. прогиб и угол поворота в начале координат; определяются из граничных условий;

М₀, Q₀ – статические начальные параметры, т.е. изгибающий момент и поперечная сила в начале координат; они определяются по схеме нагружения балки или из уравнений ее равновесия;

M_i, F_i, q_i – момент, сосредоточенная сила и распределенная нагрузка в i-м сечении балки соответственно; они включаются в уравнение со своими знаками в соответствии с «правилом зонтика» для изгибающего момента;

k_i – величина, характеризующая неравномерно распределенную нагрузку, например, треугольную или трапециевидную; определяется как тангенс угла наклона неравномерной нагрузки, k = tg a ;

Рассмотрим общий порядок определения перемещений методом начальных параметров на примере расчетной схемы некоторой балки (рисунок 2.7), который сводится к следующему:

1 Выбирается начало координат в одном из крайних сечений балки (лучше в левом), которое является общим для всех участков.

2 Для последнего силового участка балки составляется универсальное уравнение упругой линии балки (УУУЛБ)

3 Определяются начальные параметры УУУЛБ:

— геометрические начальные параметры

-статические начальные параметры определяются из уравнений равновесия

4 Все найденные начальные параметры подставляются в исходное УУУЛБ:

путем дифференцирования которого получают универсальное уравнение углов поворота балки (УУУПБ)

5 Определяются искомые перемещения точек балки путем подстановки в соответствующее уравнение числовых значений абсцисс заданных точек. При этом отбрасываются те слагаемые соответствующих универсальных уравнений, которые учитывают внешние нагрузки, приложенные за пределами рассматриваемого участка.

Изложенный выше метод начальных параметров является достаточно простым и универсальным, т.к. позволяет находить линейные и угловые перемещения любых точек балки, с большим количеством силовых участков и с разнообразной нагрузкой. Однако этот метод имеет следующие недостатки:

— он не применим для балок с ломаной осью, рамных систем и кривых брусьев;

— он не позволяет определять перемещения точек балки в произвольных направлениях, не считая вертикального.

Для устранения этих недостатков в курсе сопротивления материалов широко применяются так называемые энергетические способы.

Дата добавления: 2015-02-10 ; просмотров: 300 ; Нарушение авторских прав

Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

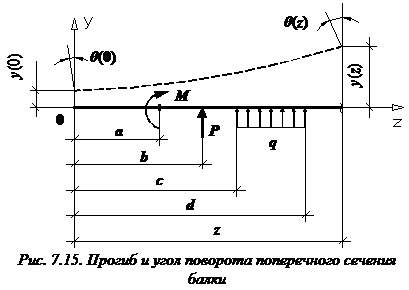
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб 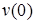и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Уравнение упругой линии балки на примере

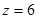
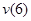
Определим прогиб балки на консоли при м, то есть . Запишем универсальное уравнение упругой линии балки :

Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: .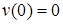

Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.

,

.

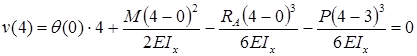
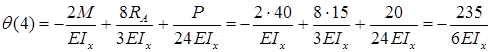
Прогиб консоли при z=6м:

Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).

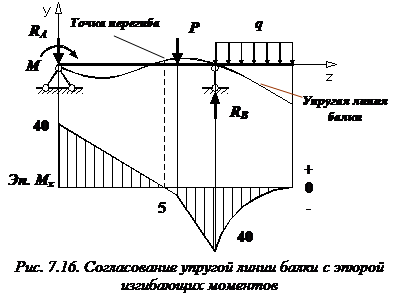
Примерный вид упругой линии балки показан на рис. 7.16.

Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.

Лекция 8

Статические моменты площади.

Осевые, полярный и центробежные моменты инерции плоской фигуры.

Главные оси и главные моменты инерции.

Моменты инерции простых фигур.

Изменение моментов инерции при параллельном переносе и повороте осей координат.

Алгоритм определения главных центральных осей и вычисления главных центральных осевых моментов инерции.

Особенности расчёта геометрических характеристик тонкостенных сечений.

Лекция 9

Виды изгиба стержня.
Внутренние силовые факторы и дифференциальные зависимости при прямом поперечном изгибе.
Чистый прямой изгиб.
Гипотезы о напряжённом и деформированном состоянии.
Вывод основных зависимостей при прямом чистом изгибе.
Касательные напряжения при поперечном изгибе.
Расчёт на прочность по допускаемым напряжениям.
Рациональные формы поперечных сечений балок.

Лекция 10

Дифференциальное уравнение оси изогнутого стержня.
Универсальное уравнение упругой линии.
Расчёт на жёсткость.

Лекция 11

Косой изгиб и внецентренное растяжение и сжатие стержней большой жёсткости.
Определение напряжений и перемещений.
Расчёт на прочность и жёсткость.
Оценка влияния поперечных и продольных сил.
Понятие о ядре сечения.

Лекция 12

Потенциальная энергия деформации стержня при произвольном нагружении.
Определение напряжений.
Принцип Лагранжа для деформируемого твёрдого тела.
Теорема Лагранжа.
Теорема Кастилиано.

Лекция 13

Определение перемещений с помощью интеграла Мора.
Способ Верещагина вычисления интеграла Мора.

Лекция 14

Расчёт винтовых цилиндрических пружин.

Лекция 15

Статически неопределимые стержневые системы.
Понятие о степенях свободы и связях.
Метод сил.
Коэффициенты канонических уравнений.
Определение перемещений в статически неопределимых системах.
Способы проверки правильности решения.