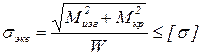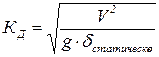Перемещения и деформации

Первоначальная длина стержня равна l. После приложения растягивающей силы длина стержня стала l1. Величина 
1. Абсолютным укорочением в направлении оси x
2. Средним удлинением
4. Абсолютным удлинением

Задание № 1.4.2.
Под действием системы внешних сил точки тела меняют положение в пространстве. Полное перемещение точки тела А в общем случае …
Варианты ответа:
1. Можно разложить на две составляющие по направлениям координатных осей
2. Является скалярной величиной
4. Можно разложить на три составляющие по направлениям координатных осей




Задание № 1.4.3.
Количественная мера изменения геометрических размеров в окрестности точки называется…
1. Деформированным состоянием в точке
2. Абсолютным удлинением стержня
3. Полным перемещением точки
4. Линейной деформацией







Величина 
Задание № 1.4.4.
В результате действия внешних сил на деформируемое тело точка К заняла новое положение К1. Вектор 
1. Угловой деформацией
2. Проекцией вектора перемещения
3. Линейной деформацией
4. Полным перемещением

В результате действия внешних сил на деформируемое тело точка К заняла новое положение К1. Вектор 
Задание № 1.4.5.
Упрощение, на основании которого при составлении уравнений равновесия тело, после нагружения внешними силами рассматривают как недеформированное, называется…
1. Условием неразрывности деформаций
2. Принципом независимости действия сил
4. Принципом начальных размеров
Ответ верный!Все твердые тела под действием внешних сил деформируются, то есть меняют свои размеры. Для подавляющего большинства тел перемещения точек являются малыми по сравнению с геометрическими размерами тела. На основании малости перемещений в методику анализа внутренних сил в теле вводят упрощение. Это упрощение носит название «принцип начальных размеров».

Угловым перемещением сечения (см. рис.) является величина…
3.

Ответ верный!При плоском изгибе поперечное сечение стержня, в общем случае, имеет два перемещения: линейное (прогиб 


[1] ДЕ — дидактическая единица — одна из предметных тем, подлежащих обязательному освещению в процессе подготовки специалистов, обучающихся по данной дисциплине (предмету).
с пояснениями
Дата добавления: 2014-11-28 ; просмотров: 4774 ; Нарушение авторских прав
ДЕ №1 ВВЕДЕНИЕ В КУРС
1. Основные понятия, введения допущения и принципы
2. Модели прочностной надежности
3. Внутренние силы и напряжения.
4. Перемещение и деформация.
ДЕ №2 РАСТЯЖЕНИЕ И СЖАТИЕ
5. Продольная сила. Напряжения и деформации
6. Испытание конструкционных материалов на растяжение и сжатие.
7. Механические свойства материалов
8. Расчеты стержней на прочность и жесткость
ДЕ №3 СДВИГ. КРУЧЕНИЕ
9. Чистый сдвиг. Расчет на сдвиг (срез)
10. Крутящий момент. Деформации и напряжения
11. Расчет на прочность при кручении.
12. Расчет на жесткость при кручении
ДЕ №4 НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ТОЧКЕ
13. Виды напряженного состояния
14. Оценка прочности материала при сложном напряженном состоянии. Теории прочности
15. Деформированное состояние в точке. Связь между деформациями и напряжениями
16. Напряженное состояние в точке. Главные площадки и главные напряжения
ДЕ №5 ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ СТЕРЖНЕЙ (-МГ)
17. Статические моменты. Центр тяжести плоской фигуры
18. Осевые момента инерции. Зависимость между моментами инерции при параллельном переносе осей
19. Главные оси и главные моменты инерции
20. Моменты инерции простых и сложных сечений
ДЕ №6 ПЛОСКИЙ ПРЯМОЙ ИЗГИБ
21. Поперечная сила, изгибающий момент и их эпюры
22. Напряжения в поперечном сечении стержня при плоском изгибе
23. Расчет балок на прочность
24. Перемещения при изгибе. Расчет балок на жесткость
ДЕ №7 СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
25. Определение перемещений с помощью интегралов Мора. Правило Верещагина
26. Статическая неопределимость. Степень статической неопределенности
28. Расчет простейших статически неопределимых систем
ДЕ №8 УСТОЙЧИВОСТЬ ПРЯМЫХ СТЕРЖНЕЙ
29. Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
30. Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
31. Влияние условий закрепления концов стержня на величину критической силы
32. Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость
ДЕ №9 СЛОЖНОЕ СОПРОТИВЛЕНИЕ ДЛЯ СТЕРЖНЕЙ (-АК)
33. Виды нагружения стержней
34. Пространственный косой изгиб
35. Изгиб с растяжением-сжатием
36. Изгиб с кручением
ДЕ №10 СОПРОТИВЛЕНИЕ ДИНАМИЧЕСКИМ И
ПЕРИОДИЧЕСКИ МЕНЯЮЩИМСЯ ВО ВРЕМНИ НАГРУЗКАМ (-ДП, -АК?)
37. Расчеты на прочность с учетом сил инерции
38. Прочность при ударных нагрузках
39. Расчеты на прочность при колебаниях
40. Расчеты на прочность при напряжениях, периодически меняющихся во времени
- Основные понятия, введения допущения и принципы
Свойство материала тела восстанавливать свои первоначальные размеры после снятия внешних сил называется
В соответствии с принципом независимости действия сил (принцип суперпозиции)
результат действия системы сил равен сумме результатов действий каждой силы в отдельности
Сопротивление материалов – это наука о методах расчета элементов инженерных конструкций на…
прочность, жесткость и устойчивость
Механическое свойство, характеризующее способность материала сопротивляться его разрушениюподдействием внешних сил, называется…
Утверждение, что напряжения и перемещения в сечениях, удаленных от места приложения внешних сил, не зависят от способа приложения нагрузки, называется…
Способность конструкции, элементов конструкции сопротивляться внешним нагрузкам в отношении изменения формы и размеров называется…
- Модели прочностной надежности
Если не учитывается конкретная структура материала (зернистая, кристаллическая и др.), и считается, что материал непрерывно заполняет весь объем элемента конструкции, то материал обладает свойством
Материал, у которого механические свойства во всех направлениях одинаковы, называется
Тело, длина которого l существенно превышает характерные размеры поперечного сечения (ширины и высоты) b и h , называется
Величины, служащие мерой механического действия одного материального тела на другое, называются
внешними силами (нагрузками)
Внешние силы, действующие на элемент конструкции, подразделяют на
сосредоточенные, распределенные и объемные силы
Объект, освобожденный от особенностей, несущественных при решении данной задачи, называется
В сопротивлении материалов относительно структуры и свойств материала принимаются гипотезы
сплошности, однородности, изотропности и идеальной упругости материала
Положение, согласно которому материал полностью заполняет весь объем тела, называется …
Разделение тела на части под действием внешних нагрузок называется…
- Внутренние силы и напряжения.
Вектор полного напряжения на данной площадке р раскладывают на составляющие (на нормаль к площадке и на плоскость этой площадки). Эти составляющие называют
нормальными (σ) и касательными ( 
Приращение сил взаимодействия между частицами (частями) тела, возникающих при его нагружении, называется
Составляющие главного вектора R и главного момента М внутренних сил по координатным осям X, Y, Z называют
внутренними силовыми факторами или внутренними усилиями в сечении стержня
Проекция главного вектора R внутренних сил на ось (Х или У), лежащую в плоскости сечения, называется
поперечной силой Qx (или Qy )
Суммарный момент относительно оси стержня всех внутренних сил, действующих в поперечном сечении, называется
Силы взаимодействия между частями рассматриваемого тела называются
Для определения внутренних силовых факторов, действующих в сечении тела, используется
Векторная величина, которая характеризует интенсивность распределения внутренних сил по сечению тела, называется
полным напряжением в точке
В системе СИ напряжение измеряется в
- Перемещение и деформация
Под действием системы внешних сил точки тела меняют положение в пространстве. Полное перемещение точки тела А в общем случае …
можно разложить на три составляющие по направлениям координатных осей
Угловым перемещением сечения (см. рис.) является величина
φ его поворота относительно одной из поперечных осей
Количественная мера изменения геометрических размеров в окрестности точки называется
В результате действия внешних сил на деформируемое тело точка К заняла новое положение К1. Вектор КК1 называется
Упрощение, на основании которого при составлении уравнений равновесия тело, после нагружения внешними силами рассматривают как недеформированное, называется…
принципом начальных размеров
Первоначальная длина стержня равна l. После приложения растягивающей силы длина стержня стала l1. Величина Δl = l1 – l называется
Отношение абсолютного удлинения Δl (укорочения) стержня к первоначальной длине l называется
Отношение абсолютного сдвига ΔS к расстоянию между сдвигающимися плоскостями a называется…
При линейном напряженном состоянии Закон Гука выражается зависимостью
Деформации (линейные ε и угловые γ) считаются практически
малыми, если они не превосходят…
- Продольная сила. Напряжения и деформации
Продольная сила N на участке равна сумме сил слева (или справа) от участка. Удобно рассчитывать N от свободного конца, чтобы не вычислять реакцию опоры.
Абсолютное удлинение ΔL стержня с длиной L и площадью сечения А равно
ΔL = N·L/(E·A). Часто встречается круглое сечение A=π·d 2 /4.
Продольная деформация ε на участке равна ε= N·/(E·A).
Знак деформации или удлинения (растягивающая или сжимающая) зависят от знака продольной силы.
Из гипотезы плоских сечений следует, что вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения нормальные напряжения σ при растяжении − сжатии прямолинейных стержней распределяются по площади поперечного сечения равномерно и равны σ=N/A.
Распределение напряжений по длине стержня, как и N, зависит от приложенных сил.
- Испытание конструкционных материалов на растяжение и сжатие.
Материал является хрупким, если образец из него разрушается при очень малых остаточных деформациях. (от 0,1 до 5%). Вид разрушенн0го образца (чугун) после испытания представлен на рисунке.



Диаграммой растяжения образца является диаграмма
После испытаний образца длиной L0 на растяжение относительное остаточное удлинение при разрыве δ в процентах составляет δ=100·(L-L0 )/ L0, где L- длина расчетной (без шейки) части после разрыва.
Относительное остаточное сужение после разрыва 
Чем меньше δи 
Чугун и сталь–материалы изотропные. Примером анизотропного материала являетсядревесина
Механические свойства материалов
На диаграмме растяжения 

точка D – пределу прочности — ( 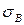
Максимальная сила разрыва 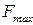

До предела пропорциональности модуль упругости постоянный и равен 
Допускаемое напряжение [s] для материала будет равно 

Конструкционные материалы делятся на хрупкие и пластичные в зависимости от величины относительного остаточного удлинения при разрыве.( 0,05 (или 5%))
Коэффициентом Пуассона 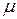
Наклеп (нагартовка) – повышение упругих свойств материала в результате предварительного пластического деформирования.
Модуль сдвига 






Модуль сдвига связан с модулем упругости и коэффициентом Пуассона зависимостью 
- Расчеты стержней на прочность и жесткость
Допускаемая нагрузка при растяжении или сжатии равна произведению допускаемого напряжения на площадь сечения.
Расчет на жесткость обычно 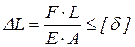

В задачах на фермы усилия в стержнях определяются их условия равновесия узлов.
Во многих задачах тестов усилие в стержнях находят из уравнения равновесия моментов относительно шарнирной опоры.
В стержнях из хрупких материалов необходимо отдельно определять допускаемые напряжения на растяжение и сжатие (бетон, чугун) и условие прочности 
- Чистый сдвиг. Расчет на сдвиг (срез)
Чистым сдвигом называют напряженное состояние, когда на гранях выделенного элемента возникают только касательные напряжения.
Правило, согласно которому на взаимно перпендикулярных площадках элемента, выделенного из тела, касательные напряжения равны по величине и направлены к общему ребру (или от него), называю законом парности касательных напряжений
Закон Гука при сдвиге выражается зависимостью 

Угловая деформация или угол сдвига 
В практических расчетах вводится допустимое касательное напряжение среза 


- Крутящий момент. Деформации и напряжения
Деформацию стержня, при которой в поперечных сечениях возникает только крутящий момент, называют кручением.
При кручении длина стержня не меняется (приближенно).
При деформации кручение угол взаимного поворота двух сечений, отнесенный к расстоянию между ними, называется относительным углом закручивания 
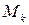
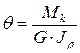
Угол закручивания 

Касательные напряжения при кручении стержня круглого поперечного сечения на радиусе 

Максимальные касательные напряжения в стержне диаметром d вычисляются по формуле 

Крутящий момент в сечении определяется как сумма внешних моментов справа или слева от сечения. Проще считать от свободного конца, не вычисляя реактивный момент в опоре.
- Расчет на прочность при кручении
Условие прочности при кручении 

для кольца 
Напряженное состояние при кручении – чистый сдвиг.
Для круга из условия прочности при кручении 
Для пластичного материала 
При проектном расчете должны быть известны максимальный крутящий момент и допускаемое напряжение – нужно определить диаметр.
При проверочном расчете должны быть известны максимальный крутящий момент, допускаемое напряжение и диаметр – нужно проверить условие прочности.
12. Расчет на жесткость при кручении
Жесткостью поперечного сечения круглого стержня при кручении называется выражение 
Условие жесткости при кручении стержня круглого поперечного сечения, с неизменным по длине диаметром имеет вид 


Если задан допустимый угол взаимного поворота двух сечений на расстоянии L 
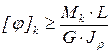
ДЕ №4
13. Виды напряженного состояния
Напряженное состояние называется линейным, если на двух взаимно перпендикулярных площадках отсутствуют напряжения. Типичные примеры: растяжение стержня, опасная точка (точка на поверхности) при изгибе стержня, одна площадка не нагружена, а на остальных равны произведение нормальных напряжений и квадрат касательного .
Напряженное состояние называется плоским, если на одной площадке отсутствуют напряжения.
Типичные примеры: стержень.
 |


Типичный пример: кручение стержня.
Общий подход: вычисляем инварианты напряженного состояния 


Тогда: линейное напряженное состояние — 
плоское напряженное состояние — 
Чистый сдвиг —
Вопрос «указать вид напряженного состояния» в конкретном случае нагружения стержня решается указанием напряжений, соответствующих растяжению, изгибу или кручению с учетом закона парности напряжений.
- Оценка прочности материала при сложном напряженном состоянии. Теории прочности
В точке всегда существуют три взаимно перпендикулярные площадки, на которых отсутствуют касательные напряжения (см. п. 16) – главные площадки. Нормальные напряжения на этих площадках – главные напряжения 
Состояние, при котором происходит качественное изменение свойств материала, переход от одного механического состояния к другому, называется предельным напряженным состоянием
Напряжение, которое следует создать в растянутом стержне, чтобы его состояние было равноопасно с заданным напряженным состоянием, называют эквивалентным напряжением.
Условия прочности в точке: эквивалентное напряжение 
Эквивалентное напряжение вычисляется по одной из теорий (гипотез) прочности.
· Согласно теории наибольших касательных напряжений (третья теория прочности для пластичных материалов),

для стержней по напряжениям в поперечном сечении 
для круглых стержней без учета растяжения 
· Согласно теории наибольших относительных линейных деформаций (вторая теория прочности для хрупких материалов),

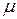
· Согласно теории потенциальной энергии формоизменения (четвертая теория прочности для пластичных материалов)
для стержней по напряжениям в поперечном сечении 
для круглых стержней без учета растяжения 
· Согласно теории Мора (пятая теория прочности, применяется для материалов с разной прочностью на растяжение и сжатие).

где 

При сравнении различных напряженных состояние наиболее опасным считается такое, при котором эквивалентное напряжение по выбранной теории прочности максимально.
Число, показывающее, во сколько раз следует одновременно увеличить все компоненты напряженного состояния, чтобы оно стало предельным, называется коэффициентом запаса для данного напряженного состояния.
Два напряженных состояния называются равно опасными, если они имеют одинаковые коэффициенты запаса.
- Деформированное состояние в точке. Связь между деформациями и напряжениями
Совокупность линейных и угловых деформаций, возникающих по различным осям и в различных плоскостях, проходящих через данную точку тела, называют деформированным состоянием в точке.
Компоненты тензора деформаций в произвольных осях 

Три взаимно перпендикулярные оси, в системе которых отсутствуют угловые деформации, называют главными осями деформированного состояния.
Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций носит название обобщенного закона Гука
Главные (линейные) деформации связаны с главными напряжениями зависимостями:



Относительное изменение объема равно

Удельная потенциальная энергия деформации изменения формы определяется выражением

- Напряженное состояние в точке. Главные площадки и главные напряжения
Совокупность напряжений, возникающих на множестве площадок, проходящих через рассматриваемую точку, называют напряженным состоянием в точке.
Площадки в исследуемой точке напряженного тела, на которых касательные напряжения равны нулю, называют главными площадками.
В растянутом стержне главные площадки совпадают с поперечным и продольными сечениями.
Значения главных напряжений определяют из решения кубического уравнения 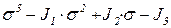
При чистом сдвиге (кручении) главные напряжения равны 
Тензор напряжений – этосовокупность нормальных и касательных компонентов напряжений на трех взаимно-перпендикулярных элементарных плоскостях, проходящих через точку тела.
Максимальные касательные напряжения в точке действуют в плоскости главных напряжений 


Угол наклона 

- Статические моменты. Центр тяжести плоской фигуры
Статические моменты площади фигуры относительно оси x, y определяется интегралами:


Упрощенное вычисление – произведение площади сечения на расстояние от оси до центра тяжести сечения. Для сложной фигуры – сумма соответствующих произведений составляющих фигур.
Ось, относительно которой статический момент площади сечения равен нулю, называется центральной. Центральные оси пересекаются в центре тяжести сечения. Общий подход к определению расстояния от центра тяжести сечения до оси:


Центр тяжести треугольника лежит на пересечении медиан, т.у. отстоит от основания на 1/3 высоты.
Центр тяжести полуокружности отстоит от диаметра на 
- Осевые момента инерции. Зависимость между моментами инерции при параллельном переносе осей
Осевые моменты инерции площади фигуры относительно оси x, y определяется интегралами:


Для простых сечений:
Прямоугольник высотой 



— относительно сторон 

Равнобедренный треугольник высотой 



— относительно основания 
Окружность диаметром d — относительно центральной оси 
Полуокружность диаметром d относительно центральных осей 

Для сложной фигуры из k простых 
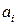
- Главные оси и главные моменты инерции
Главными называются оси, относительно которых центробежный момент инерции

Или: оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями. Главные оси инерции можно провести через любую точку плоской фигуры.
Если одна из осей является осью симметрии – оси главные. Сумма моментов инерции при повороте осей не меняется.
В главных осях моменты инерции экстремальны относительно повернутых. Как следствие, при равных главных моментах инерции все повернутые оси главные.
- Моменты инерции простых и сложных сечений
Вся теория изложена выше.
- Поперечная сила, изгибающий момент и их эпюры
Связь поперечной силы и погонной нагрузки 
Связь изгибающего момента и поперечной силы 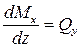
Поперечная сила Qy в произвольном поперечном сечении стержня численно равна алгебраической сумме проекций на ось y всех внешних сил, расположенных по одну сторону от рассматриваемого сечения.
Момент 
Правило знаков для поперечной силы Qy и изгибающего момента Мz изображено на рисунке… .
- Напряжения в поперечном сечении стержня при плоском изгибе
При плоском поперечном изгибе нормальные напряжения по ширине сечения балки распределяются равномерно.
При плоском изгибе стержня нормальные напряжения по высоте поперечного сечения имеют линейный закон распределения; равны нулю на нейтральной линии и достигают максимума в точках, наиболее удаленных от нее.
Нормальные напряжения в точке с координатой 

Максимальные нормальные напряжения в сечении определяются формулой 
где момент сопротивления 


Вывод формулы для определения нормальных напряжений при чистом изгибе основывается на гипотезе плоских сечений и гипотезе об отсутствии взаимного надавливания продольных слоев балки.
Касательные напряжения при плоском поперечном изгибе определяются по формуле 



Для прямоугольного сечения
Направление касательных напряжений соответствует направлению суммы внешних сил слева от сечения. Направление касательных напряжений в продольном сечении определяется по закону парности касательных напряжений.
- Расчет балок на прочность
Расчет ведется по нормальным напряжениям (т.к. касательные для не тонкостенных балок значительно меньше нормальных).
Проверка на прочность по касательным напряжениям необходима в случае, если короткие балки нагружены перпендикулярно продольной оси силами, имеющими большое значение; материал балки плохо сопротивляется сдвиговым деформациям; ширина поперечного сечения балки в районе нейтральной оси мала.
Для пластичных материалов с одинаковой прочностью на растяжение и сжатие (сталей) 

Для хрупких материалов с разной прочностью на растяжение и сжатие (чугунов) расчет ведут отдельно для сжатых и растянутых слоёв.
Лучше работать на изгиб при данных условиях закрепления и нагружения будет балка, у которой сечение ( 

Полная проверка прочности балки при изгибе включает в себя проверку по нормальным напряжениям, проверку по касательным напряжениям и проверку по главным напряжениям.
Наиболее выгодным с точки зрения экономии массы является сечение, у которого при равенстве моментов сопротивления минимальное отношение площадей. При конкретном 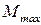
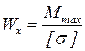

В общем случае поперечного изгиба 
- Перемещения при изгибе. Расчет балок на жесткость
В сечении возникают прогибы 
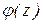
В опоре прогиб равен нулю. При 


В общем случае прогиб и угол поворота в точке А определяются по способу Верещагина: 







В частных случаях:
· При равномерной погонной нагрузке на шарнирную балку в ее центре 
· В точке приложения силы F на шарнирную балку в центре 
· В точке приложения силы F на консольную балку на свободном конце 
· В точке приложения момента 

Во многих простых задачах полезно изобразить вид прогиба и ответить на поставленные вопросы. Например:

Аналогично во многих других простых задачах.
- Определение перемещений с помощью интегралов Мора. Правило Верещагина
Для определения перемещений (обобщенных) при плоском изгибе применяется интеграл Мора 
При поперечном изгибе более точная формула (с учетом сдвига от поперечной силы) —
Если стоит задача определения полного перемещения 



26. Статическая неопределимость. Степень статической неопределенности
Степень статической неопределимости – число дополнительных связей 
Связи иногда разделяют на внешние 

Защемление — 
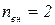

Врезанный шарнир внутри контура — 
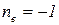

Число связей, при котором достигается кинематическая неизменяемость системы, носит название_ необходимого числа связей. В плоской конструкции число необходимых связей, обеспечивающих равновесие, равно 3.
В плоской конструкции 
Система (исходная), освобожденная от дополнительных связей, статически определимая и кинематически неизменяемая, носит название основной системы.
Число отброшенных дополнительных связей равно 
Реакции отброшенных связей обозначаются 
Для определения 

Система канонических уравнений имеет вид 








Физический смысл системы канонических уравнений состоит в том, что они являются уравнениями совместности деформаций.
Последовательность расчета методом сил:
а) определяется степень статической неопределимости 
б) составляется основная система,
в) записываются (и решаются) канонические уравнения.
После чего может решаться статически определимая эквивалентная система.
28. Расчет простейших статически неопределимых систем
Расчет в общем случае производится в следующем порядке:
- Строятся эпюры внутренних сил от системы внешних сил (
при изгибе,
при кручении или
при растяжении) и эпюры от единичных сил (
при изгибе,
при кручении или
при растяжении).
- Методом Верещагина вычисляются
и
.
В первом случае определяются площадь 





Во втором случае определяются площадь 




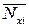

- Решается система канонических уравнений и вычисляются значения
.
- При необходимости (по условию задачи) в эквивалентной системе строятся эпюры внутренних сил, и в опасной точке вычисляются напряжения и проводится расчет на прочность или жесткость.
- Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое напряжение. Гибкость стержня
Свойство системы сохранять свое состояние при внешних воздействиях называется устойчивостью.
Критическая сила сжатого стержня – наименьшее значение осевой сжимающей силы, способной удержать стержень в изогнутом состоянии (в состоянии потере устойчивости). Другое определение – значение сжимающей силы, при которой стержень теряет способность сохранять прямолинейную форму равновесия.
Критическая сила сжатого стержня в пределах закона Гука определяется по формуле Эйлера 
где 
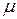
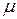
Типичные частные случаи: 

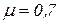


Критическим напряжением называется напряжение, возникающее в поперечном сечении сжатого стержня при воздействии нагрузки, вызывающей потерю устойчивости стержня – критической силы.
Критическое напряжение вычисляется по формуле

где 
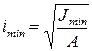
- Формула Эйлера для критической силы сжатого стержня и пределы ее применимости
Вывод формулы Эйлера основан на допущении, что деформации подчиняются закону Гука.
Использование формулы Эйлера является корректным при выполнении неравенства 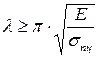

или при условии 
Для стержня из малоуглеродистой стали формула Эйлера применима, если 
В формулу Эйлера входит величина 
Формой потери устойчивости стержня при шарнирном опирании его концов является синусоида.
31. Влияние условий закрепления концов стержня на величину критической силы
Влияние заключается в изменении величины 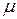
Форму потери устойчивости в простых задачах легко представить, учитывая что:
в опоре прогиб равен нулю,
в защемлении угол поворота равен нулю.
32. Устойчивость за пределом пропорциональности. Расчет сжатых стержней на устойчивость
График зависимости критического напряжения от гибкости, когда напряжение в стержне не превышает предела пропорциональности, имеет вид гиперболы.
Расчет на устойчивость за пределом пропорциональности имеет смысл, если 

Допускаемое напряжение на устойчивость связано с допускаемым напряжением на сжатие зависимостью 
Коэффициент пропорциональности 

Стержень теряет устойчивость за пределами упругости, если его гибкость меньше предельной


Для стали 


Для стали 3, например, при пределе текучести 



В последних тестах для углеродистых сталей по Ясинскому принято
При равных площадях сечения наиболее выгодным с точки зрения устойчивости является сечение с большим минимальным моментом инерции, так как имеет большую критическую силу.
33. Виды нагружения стержней
Приводим все действующие в сечении силы и моменты к главным центральным осям и определяем их проекции – внутренние силовые факторы 
Различают следующие виды нагружения стержней:
· Внецентренное сжатие – например, сжатие равнодействующей силой, приложенной на расстоянии от центра тяжести сечения; в общем случае ( 
· Изгиб с растяжением- сжатием – тоже при любом знаке N;
· Косой изгиб – например, изгиб равнодействующей силой, проходящей через центр тяжести сечения или парой сил (моментом) не в плоскости каждой из главных осей, в общем случае ( 
· Изгиб – например, изгиб равнодействующей силой, проходящей через центр тяжести сечения и совпадающей с одной из главных осей или парой сил (моментом) в плоскости одной из главных осей , в общем случае ( 
· Изгиб с кручением — изгиб равнодействующей силой, не проходящей через центр тяжести сечения и параллельной одной из главных осей, в общем случае ( 
· Косой изгиб с кручением — изгиб равнодействующей силой, не проходящей через центр тяжести сечения и не параллельной одной из главных осей , в общем случае ( 
34. Пространственный косой изгиб
Уравнение нулевой линии 
Моменты имеют одинаковый знак при одинаковом повороте против вокруг оси если смотреть с конца оси и наоборот. При одинаковом знаке моментов нулевая линия проходит через первый и третий квадрант, при разном знаке – через второй и четвертый.
Опасная точка – максимально удалена от нулевой линии.
35. Изгиб с растяжением-сжатием
Обратите внимание на обозначение осей в задачах . Левая система координат.
Что точно – знак напряжений .
Нормальные напряжения 
36. Изгиб с кручением
Вид напряженного состояния при кручении с изгибом стержня круглого поперечного сечения плоское.
В точке поверхности действуют нормальное и касательное напряжения, направленные по правилам изгиба и кручения. Учесть закон парности касательныхнапряжений.
Условие прочности по третьей гипотезе для круглого сечения
Условие прочности по четвертой гипотезе для круглого сечения
37. Расчеты на прочность с учетом сил инерции
Если к активным и реактивным силам, действующим на тело, которое движется ускоренно, добавить силы инерции, то полученная система сил будет самоуравновешенной и должна удовлетворять уравнениям равновесия статики – принцип Даламбера.
Основные задачи требуют учета центробежных сил при вращении в расчетной схеме. Сами же расчеты на прочности проводятся как обычно (см. выше).
38. Прочность при ударных нагрузках
Учет ударных нагрузок состоит в умножении статических нагрузок – веса ударяющего тела- на динамический коэффициент 
При падении с высоты Н тела весом Рстатическое , который в статике привел бы к прогибу δстатическое в точке падения,

При горизонтальном ударе того же тела со скоростью V
39. Расчеты на прочность при колебаниях
Расчеты ведутся аналогично п. 38. Отличие в том, что динамический коэффициент обозначается иначе (в примерах 
При колебаниях напряжения переменны во времени и меняются циклически. Амплитуда динамических напряжений больше статического напряжения от наибольшей величины возмущающей силы в 
Среднее напряжение цикла равно статическому значению.
В расчетах на выносливость (усталость) коэффициент концентрации напряжений отличается от обычного в том случае, если амплитуда напряжений рассчитывается без учета 
Запас по нормальным напряжениям
Частота собственных колебаний в одномассовой системе определяется по формулам 
40. Расчеты на прочность при напряжениях, периодически меняющихся во времени
Выносливость зависит от максимального 



а также от коэффициента ассиметрии цикла 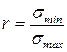




Асимптота кривой — предел выносливости 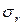
Пределом выносливости 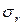

Стандартные испытания проводят при 


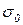





Выносливость обеспечивается при расположении рабочих значений напряжений ниже ломанной 3-2-4.
Запас прочности при 

Равновесие произвольной пространственной системы сил – решение задачи
Порядок решения задач на равновесие с произвольной пространственной системой сил
Чтобы решить задачу на равновесие твердого тела с произвольной пространственной системой сил, надо выбрать прямоугольную систему координат и, относительно нее, составить уравнения равновесия.
Уравнения равновесия, для произвольной системы сил, распределенных в трехмерном пространстве, представляют собой два векторных уравнения:
векторная сумма сил, действующих на тело, равна нулю
(1) ;
векторная сумма моментов сил, относительно начала координат, равна нулю
(2) .
Пусть Oxyz – выбранная нами система координат. Спроектировав уравнения (1) и (2) на оси этой системы, получим шесть уравнений:
суммы проекций сил на оси xyz равны нулю
(1.x) ;
(1.y) ;
(1.z) ;
суммы моментов сил относительно осей координат равны нулю
(2.x) ;
(2.y) ;
(2.z) .
Здесь мы считаем, что на тело действуют n сил, включая силы реакций опор.
Пусть произвольная сила , с компонентами , приложена к телу в точке . Тогда моменты этой силы относительно осей координат определяются по формулам:
(3.x) ;
(3.y) ;
(3.z) .
Таким образом, порядок решения задачи, на равновесие с произвольной пространственной системой сил, следующий.
- Отбрасываем опоры и заменяем их силами реакций. Если опорой является стержень или нить, то сила реакции направлена вдоль стержня или нити.
- Выбираем прямоугольную систему координат Oxyz .
- Находим проекции векторов сил на оси координат, , и точек их приложения, . Точку приложения силы можно перемещать вдоль прямой, проведенной через вектор силы. От такого перемещения значения моментов не изменятся. Поэтому выбираем наиболее удобные для расчета точки приложения сил.
- Составляем три уравнения равновесия для сил (1.x,y,z).
- Для каждой силы, по формулам (3.x,y,z), находим проекции моментов силы на оси координат.
- Составляем три уравнения равновесия для моментов сил (2.x,y,z).
- Если число переменных больше числа уравнений, то задача статически неопределима. Методами статики ее решить нельзя. Нужно использовать методы сопротивления материалов.
- Решаем полученные уравнения.
Упрощение расчетов
В некоторых случаях удается упростить вычисления, если вместо уравнения (2) использовать эквивалентное условие равновесия.
Сумма моментов сил относительно произвольной оси AA′ равна нулю:
(4) .
То есть можно выбрать несколько дополнительных осей, не совпадающих с осями координат. И относительно этих осей составить уравнения (4).
Далее приводится пример, в котором удается упростить вычисления за счет соответствующего выбора осей.
Пример решения задачи на равновесие произвольной пространственной системы сил
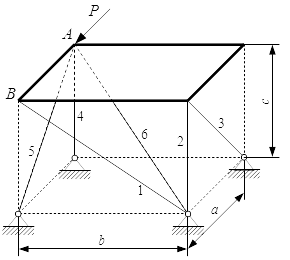
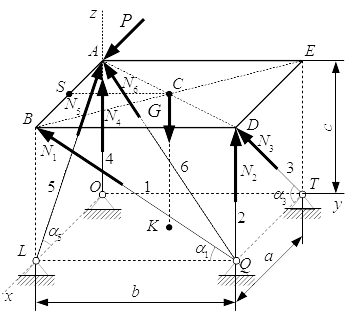
Найти реакции стержней, поддерживающих тонкую однородную горизонтальную плиту в трехмерном пространстве. Система крепления стержней показана на рисунке. На плиту действуют: сила тяжести G; и сила P, приложенная в точке A, направленная вдоль стороны AB.
Дано:
G = 28 kН ; P = 35 kН ; a = 7,5 м ; b = 6,0 м ; c = 3,5 м .
Решение задачи
Сначала мы решим эту задачу стандартным способом, применимым для произвольной пространственной системы сил. А затем получим более простое решение, основываясь на конкретной геометрии системы, за счет выбора осей при составлении уравнений равновесия.
Решение задачи стандартным способом
Этот метод хоть и приведет нас к довольно громоздким вычислениям, но он применим для произвольной пространственной системы сил, и может применяться в расчетах на ЭВМ.
Отбросим связи и заменим их силами реакций. Связями здесь являются стержни 1–6. Вводим вместо них силы , направленные вдоль стержней. Направления сил выбираем наугад. Если мы не угадаем с направлением какой-либо силы, то получим для нее отрицательное значение.
Проводим систему координат Oxyz с началом в точке O .
Находим проекции сил на оси координат.
Для силы имеем:
.
Здесь α 1 – угол между LQ и BQ . Из прямоугольного треугольника LQB :
м ;
;
.
Силы , и параллельны оси z . Их компоненты:
;
;
.
Для силы находим:
.
Здесь α 3 – угол между QT и DT . Из прямоугольного треугольника QTD :
м ;
;
.
Для силы :
.
Здесь α 5 – угол между LO и LA . Из прямоугольного треугольника LOA :
м ;
;
.
Сила направлена по диагонали прямоугольного параллелепипеда. Она имеет следующие проекции на оси координат:
.
Здесь – направляющие косинусы диагонали AQ :
м ;
;
;
.
Выбираем точки приложения сил. Воспользуемся тем, что их можно перемещать вдоль линий, проведенных через векторы сил. Так, в качестве точки приложения силы можно взять любую точку на прямой TD . Возьмем точку T , поскольку для нее x и z — координаты равны нулю:
.
Аналогичным способом выбираем точки приложения остальных сил.
В результате получаем следующие значения компонентов сил и точек их приложений:
; (точка B );
; (точка Q );
; (точка T );
; (точка O );
; (точка A );
; (точка A );
; (точка A );
; (точка K ).
Составляем уравнения равновесия для сил. Суммы проекций сил на оси координат равны нулю.
;
;
.
Составляем уравнения равновесия для моментов сил. Суммы моментов сил относительно осей координат равны нулю.
;
;
;
В этой системе шесть уравнений и шесть неизвестных. Далее сюда можно подставить численные значения и получить решение системы, используя математическую программу вычисления системы линейных уравнений.
Но, для этой задачи, можно получить решение без использования средств вычислительной техники.
Эффективный способ решения задачи
Мы воспользуемся тем, что уравнения равновесия можно составлять не единственным способом. Можно произвольным образом выбирать систему координат и оси, относительно которых вычисляются моменты. Иногда, за счет выбора осей, можно получить уравнения, которые решаются более просто.
Воспользуемся тем, что, в равновесии, сумма моментов сил относительно любой оси равна нулю. Возьмем ось AD . Сумма моментов сил относительно этой оси равна нулю:
(П7) .
Далее заметим, что все силы, кроме пересекают эту ось. Поэтому их моменты равны нулю. Не пересекает ось AD только одна сила . Она также не параллельна этой оси. Поэтому, чтобы выполнялось уравнение (П7), сила N 1 должна равняться нулю:
N 1 = 0 .
Теперь возьмем ось AQ . Сумма моментов сил относительно нее равна нулю:
(П8) .
Эту ось пересекают все силы, кроме . Поскольку сила не параллельна этой оси, то для выполнения уравнения (П8) необходимо, чтобы
N 3 = 0 .
Теперь возьмем ось AB . Сумма моментов сил относительно нее равна нулю:
(П9) .
Эту ось пересекают все силы, кроме , и . Но N 3 = 0 . Поэтому
.
Момент от силы относительно оси равен произведению плеча силы на величину проекции силы на плоскость, перпендикулярную оси. Плечо равно минимальному расстоянию между осью и прямой, проведенной через вектор силы. Если закручивание происходит в положительном направлении, то момент положителен. Если в отрицательном – то отрицательный. Тогда
.
Отсюда
kН .
Остальные силы найдем из уравнений (П1), (П2) и (П3). Из уравнения (П2):
N 6 = 0 .
Из уравнений (П1) и (П3):
kН ;
kН
Таким образом, решая задачу вторым способом, мы использовали следующие уравнения равновесия:
;
;
;
;
;
.
В результате мы избежали громоздких расчетов, связанных с вычислениями моментов сил относительно осей координат и получили линейную систему уравнений с диагональной матрицей коэффициентов, которая сразу разрешилась.
N 1 = 0 ; N 2 = 14,0 kН ; N 3 = 0 ; N 4 = -2,3 kН ; N 5 = 38,6 kН ; N 6 = 0 ;
Знак минус указывает на то, что сила N 4 направлена в сторону, противоположную той, которая указана на рисунке.
Автор: Олег Одинцов . Опубликовано: 13-11-2017
http://life-prog.ru/1_53597_s-poyasneniyami.html
http://1cov-edu.ru/mehanika/statika/ravnovesie-prostranstvennoj-sistemy-sil/


 Механические свойства материалов
Механические свойства материалов



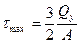


 при растяжении).
при растяжении).