Уравнение абсолютного движения жидкости в подвижной системе координат
В работе под термином «среда» понимается жидкость или газ. Однако, исходя из интуитивных соображений, мы будем употреблять термин «жидкость». Ниже перечислены гидродинамические ограничения, при выполнении которых возможно аналитическое исследование необходимых условий оптимальности для задач, упомянутых во введении. Предполагается, что выбрана инерциальная система, а в ней — правая прямоугольная декартова система координат .
Предположим, — вектор скорости частицы жидкости в точке в момент , и , , — компоненты . Первые два ограничения сводятся к следующему.
L1. Жидкость несжимаема.
С учетом уравнения неразрывности это ограничение эквивалентно тому, что скорость объемной деформации равна нулю:
L2. Выполняется обобщенная гипотеза Ньютона [22]
где — линейный оператор, определяемый тензором напряжений, — скалярное поле давления, — коэффициент динамической вязкости, — тождественное преобразование, — производная Фреше, — сопряженный оператор.
Пусть в жидкости движется ограниченных размеров тело с достаточно гладкой границей . Одним из постулатов механики жидкости является условие прилипания: вблизи поверхности тела векторы скорости частиц жидкости совпадают с векторами скорости соответствующих точек поверхности тела. Из этого условия и ограничения L1 вытекает, что в случае поступательного движения на поверхности тела выполняется равенство [22]
где — единичный вектор внешней нормали к поверхности в точке
Напряжение на площадке поверхности тела подсчитывается по формуле , где — единичный вектор внешней нормали к площадке . Отсюда с учетом (2.2) получится формула для главного вектора сил, действующих со стороны жидкости на поверхность движущегося тела (гидродинамических сил):
Формула для главного момента гидродинамических сил получается аналогично. Cогласно (2.3), если тело движется поступательно, формула (2.4) сводится к равенству
Далее понадобится так называемая подвижная система координат
с началом в центре инерции тела и осями, жестко связанными с телом.
Для нахождения главного вектора и главного момента необходимо вычислить на поверхности тела давление и производную Фреше вектора скорости движения жидкости. Последнее связано с решением некоторой граничной задачи для векторного уравнения Навье-Стокса. Ниже это уравнение выписано в подвижной системе координат с осями, параллельными соответствующим осям системы (считается, что тело движется поступательно). Пусть — вектор скорости движения тела и — радиус-вектор его центра инерции. Для векторов абсолютных скоростей движения жидкости и давления в подвижной системе координат примем обозначения
Тогда уравнение Навье-Стокса имеет вид
где — напряженность поля силы тяжести, — плотность жидкости, — коэффициент кинематической вязкости.
Теперь упомянутая выше граничная задача сводится к нахождению решения системы уравнений в частных производных, состоящей из уравнения (2.6) и уравнения неразрывности . Это решение должно удовлетворять условию прилипания , а также естественному условию вида .
Обтекание называется установившимся, если поле его абсолютных скоростей в подвижной системе не изменяется с течением времени. Ясно, что в случае поступательного движения тела стационарное обтекание возможно лишь при условии, что .
Ниже приведены формулы для силы лобового сопротивления, действующей на однородный шар, в стационарных случаях, рассмотренных Стоксом и Озееном.
Метод Стокса пренебрегает в уравнении (2.6) напряженностью гравитационного поля и слагаемым . В результате для величины силы сопротивления движению шара получается выражение , где есть величина вектора скорости , — радиус шара. Для последующих обобщений этому выражению удобно придать форму
Здесь , — коэффициент лобового сопротивления, — число Рейнольдса.
Подход Озеена по-прежнему пренебрегает действием гравитационных сил и квадратичными членами инерции, но полностью учитывает скорость движения шара в уравнении Навье-Стокса. Получается следующий приближенный результат:
Пусть тело обладает осью симметрии. Тогда в случае движения, в процессе которого его ось симметрии не покидает заданной плоскости, например, вертикальной плоскости , согласно теоремам статики абсолютно твердого тела система сил воздействия жидкости на тело может быть приведена к равнодействующей, называемой гидродинамической силой. Как принято (см., например, [23]), точка пересечения оси симметрии с линией действия гидродинамической силы называется центром давления. Эту силу обычно разлагают на две составляющие, первая из которых имеет направление, коллинеарное вектору скорости движения центра инерции тела а вторая — направление, перпендикулярное . Первую составляющую называют силой лобового сопротивления, а вторую — подъемной силой.
Пусть — единичные орты системы координат . Далее понадобится преобразование, ставящее в соответствие вектору вектор . Пусть — величина вектора скорости центра масс тела , — величина силы лобового сопротивления, — величина подъемной силы. Справедливо утверждение, которое удобно для последующих ссылок сформулировать в виде леммы.
Лемма 1.1. Сила лобового сопротивления и подъемная сила рассчитываются по формулам
где — единичный вектор, направление которого совпадает с осью симметрии тела.
Представление (2.7) (или (2.8)) для величины действующей на шар силы лобового сопротивления выбрано так, чтобы коэффициент был безразмерной величиной. Это представление можно сохранить для величины стационарной силы лобового сопротивления и в рассматриваемом случае, т.е.
Аналогично, величина стационарной подъемной силы представима в виде
Здесь — площадь проекции тела на плоскость, перпендикулярную вектору скорости движения его центра инерции.
Согласно теории динамического подобия коэффициенты и зависят только от формы тела, чисел Рейнольдса и Фруда.
Далее рассматриваются системы из осесимметричных тел (называемых звеньями). Введем еще одно ограничение.
L3. Движение систем происходит в объеме жидкости либо большой протяженности, либо заключенном внутри твердых границ.
В рамках перечисленных ограничений коэффициент является [11] функцией только формы тела, числа Рейнольдса и, возможно, угла атаки между вектором скорости перемещения центра инерции тела и его осью симметрии, т.е. форма, . Для определения угла атаки можно использовать формулу
Обращаясь к случаю нестационарного обтекания, следует отметить, что Буссинеск обобщил подход Стокса на случай неравномерного поступательного движения шара и получил формулу для силы лобового сопротивления [19], которая в терминах операции обобщенного дифференцирования и обобщенной свертки [18] (обозначаемой ниже символом « ») имеет вид
Здесь приняты обозначения
Первый член формулы (2.13) — инерционная составляющая сопротивления, соответствующая так называемой присоединенной массе, а второй, , представляет стационарную формулу Стокса.
Если сила лобового сопротивления и подъемная сила могут быть достаточно точно описаны при помощи формул (2.9)-(2.11), то обтекание называют квазистационарным [11].
Далее работа гидродинамических сил рассматривается как оценка качества процесса управления. В разделе 3 показано, что решение задачи об оптимальном перемещении шара в предположении квазистационарности обтекания приводит к относительной ошибке в оптимальных энергетических затратах всего лишь порядка 0,02 % (предполагается, что числа Рейнольдса ). Нестационарность обтекания может быть частично учтена путем введения присоединенной массы [11,12].
Гипотеза 1. Оптимальное перемещение системы порождает квазистационарное обтекание ее звеньев.
Лемма 1.2. Пусть выполнены ограничения L1-L3 , справедлива гипотеза 1 и коэффициент лобового сопротивления каждого звена системы является однородной функцией степени чисел Рейнольдса, соответствующих оптимальному движению системы. Тогда для каждого звена величина силы лобового сопротивления является однородной функцией степени от величины скорости его центра инерции. То же самое верно и для подъемных сил.
Замечание. Для тел сферической или цилиндрической формы коэффициент лобового сопротивления является практически однородной функцией достаточно малых чисел Рейнольдса, когда он приблизительно обратно пропорционален им, а также достаточно больших чисел Рейнольдса, когда он незначительно зависит от них (в частности, такие числа образуют довольно протяженную левую полуокрестность числа ). В первом случае , а во втором .
Гипотеза 2. Оптимальные перемещения систем обладают следующим свойством: числа Рейнольдса, соответствующие каждому звену, таковы, что коэффициенты лобового сопротивления и подъемной силы звена являются однородными функциями некоторой степени этих чисел.
Уравнения движения в форме Ламба
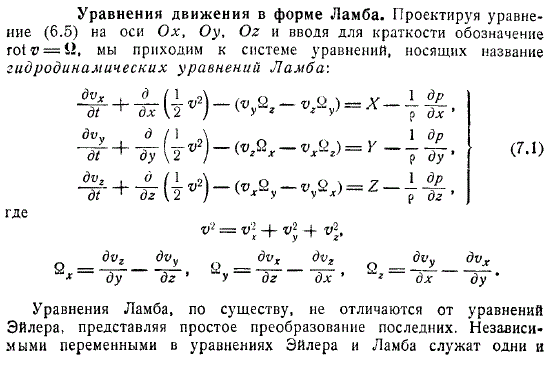



Форма Ламба
Если вы создадите уравнения на оси и введете нотацию для краткости, это будет система уравнений, называемая гидродинамическим уравнением. Уравнение по существу совпадает с уравнением Эйлера и представляет собой простое преобразование уравнения Эйлера. С преобразованием гидромеханики предыдущего абзаца, вы можете написать. Здесь простое число относительно производной означает, что производная происходит в движущейся системе координат.
Таким образом, уравнение относительного движения. В некоторых случаях, используя движущуюся систему координат, полезно рассмотреть абсолютное движение жидкости.Прежде всего, следует отметить, что если есть абсолютный остаток жидкости, то именно поэтому предыдущая формула приведет к соотношению, которое, конечно же, придется поставить.
Однако векторные формы уравнений движения эта идентичность может быть установлена непосредственно. Затем мы добавляем равенство и используем его. Теперь это с помощью этих уравнений предыдущие соотношения принимают.
Уравнения и расчёты
Это уравнение абсолютного движения жидкости в движущейся системе координат. Здесь также показано уравнение относительного движения жидкости и уравнение абсолютного движения жидкости, связанное с движущейся системой координат. Наряду с неподвижной системой координат вводится подвижная система координат, движение которой характеризуется вектором скорости подвижной системы координат и вектором угловой скорости этой системы координат.
| Для цилиндрических координат: | Для криволинейных координат: |
| tf,= 1, Н56 = г, /У3 = 1. | grad 45Vr — Vr4X |
| tf,= 3, Н43 = г, /У3 = 1. | grad 1Vr — Vr5X |
| tf,= 4, Н56 = г, /У3 = 1. | grad 86Vr — Vr8X |
| tf,= 5 Н97 = г, /У3 = 1. | grad 03Vr — Vr2X |
В данный момент уравнения движения в форме Лагранжа мы предполагаем, что обе системы координат совпадают друг с другом, и обозначим радиус вектор частицы жидкости через показывает относительный вектор скорости частицы жидкости, то есть ее скорость относительно движущейся системы координат.
Через транзита со скоростью транспорта вектор абсолютной скорости частицы жидкости. Относительное ускорение, выраженное является подобным и абсолютное ускорение частиц жидкости дает уравнение.
Происходит ускорение Кориолиса. Основные уравнения движения включают абсолютное ускорение. Таким образом, уравнение Эйлера относительного движения жидкости имеет следующие количество функций. Я также пишу уравнение с уравнением кривой.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Уравнения гидродинамики
Вы будете перенаправлены на Автор24
Гидродинамика – обширный и важный раздел гидравлики, исследующий основные законы движения идеальной жидкости и ее взаимосвязь с подвижными и неподвижными поверхностями.
Рисунок 1. Уравнение Бернулли. Автор24 — интернет-биржа студенческих работ
Движение физического вещества состоит из достаточно сложного перемещения отдельных атомов молекул. В целях упрощения длительного расчета вводится определение струйчатой модели стабильности. Согласно этой модели, весь поток включает в себя отдельные элементарные струйки, рассмотрение которых в отдельности дает шанс понять закономерности потока жидкости в целом.
С точки зрения математической формулировки движения текучих и постоянных сред, нет разницы между газом и жидкостью. Иногда жидкостью называют несжимаемое пространство, а газом называют среду, у которой начальная плотность существенно меняется со временем.
Жидкость – такое состояние физического пространства, при котором она быстро и легко деформируется под влиянием внутренних и внешних сил.
В отличие от твердого материального тела жидкость не оказывает особое сопротивления сдвиговым нагрузкам, и поэтому такому объему без труда можно придать любую форму. В то же время жидкость может самостоятельно сопротивляться нормальным напряжениям сжатия или растяжения, иногда даже намного сильнее, чем физические вещества. Данная особенность жидкости широко применяется в разнообразных гидравлических машинах и устройствах, например, в гидравлических домкратах и прессах.
Жидкость в основном характеризуется несколькими основными параметрами:
- плотность $ρ$;
- динамическая вязкость $μ$;
- теплоемкость $c$;
- теплопроводность $\lambda$.
Готовые работы на аналогичную тему
В гидродинамике исследуются математические модели течений газа и жидкости в разных условиях. Эти модели в первую очередь представляют собой концепции дифференциальных уравнений при частных и производных обстоятельствах.
Основные уравнения гидродинамики
Главными гидродинамическими уравнениями являются уравнение неразрывности или сплочённости сред, а также уравнение Бернулли.
Уравнение неразрывности представляет собой формулу стабильности расхода и записывается следующим образом:
$dQ_1 + dQ_2 = dQ = const$, где:
$Q_1, Q_2, Q$ – скорости начального движения частиц жидкости в различных живых сечениях струйки.
Для потока уравнение сплоченности сред будет выглядеть так:
Уравнение Бернулли считается фундаментальным законом гидродинамики. Оно устанавливает взаимосвязь между скоростью, давлением, и положение исследуемого элемента в пространстве. Посредством этого уравнения решается огромный круг сложных инженерных задач.
Для упрощения изучения общих и важных закономерностей, присущих постоянно движущейся жидкости, ее часто представляют в виде неизменной среды, не обладающей внутренней энергией и трением. Такую жидкость в физике называют идеальной.
Уравнение Бернулли для элементарной струйки идеальной жидкости чаще всего используется при расчетах и имеет следующий вид
- $Z$ – геометрический стабильный напор, или потенциальная удельная энергия начального положения;
- $\frac
$ — изометрический напор, или удельная сила давления; - $\frac<2>^<2><2g>$ — cкоростной напор, или кинетическая энергия.
Это уравнение также считается формулой закона сохранения и удержания энергии для движущейся жидкости. В этом заключается ее основной физический смысл.
При длительном движении реальной жидкости, обладающей определенной вязкостью, часть ее внутренней энергии автоматически затрачивается на преодоление сил трения. Этот показатель в виде тепла рассеивается в окружающую среду. Такое явление необратимо и в науке называется диссипацией. Диссипируемую величину в гидродинамике называют гидравлическими потерями.
Уравнения Навье-Стокса для несжимаемой жидкости
Рисунок 2. Уравнение Навье-Стокса. Автор24 — интернет-биржа студенческих работ
Плотность несжимаемой жидкости в любых ситуациях постоянна, в математической модели она выступает как изначальный заданный параметр. Уравнение неразрывности при этом имеет такой вид
Система уравнений всегда замкнута, так как содержит 4 формулы для трёх компонент скорости и давления.
В развернутой форме для компонент скоростного вектора $v = G$ в декартовой системе координат $ x, y, z$ уравнения Навье-Стокса для несжимаемой жидкости с постоянной вязкостью записывается так:
Взгляд на температуру как основную меру внутренней энергии, непосредственно связанную со скоростью движения атомов и молекул, используется в физике, а в гидродинамике был принят феноменологический метод, при котором исследуют макроскопические характеристики переноса тепла. В частности, вводится определение теплового потока между нагретыми частями сплошного пространства.
Тепловой поток $Q$ – это точное количество тепла, которое трансформируется в единицу времени $Q = \frac<Дж><сВт>$.
Плотность теплового постоянного потока $q = \frac$ – это протекающий через единицу площади поток.
Тепло в гидродинамике переносится разными механизмами:
- Молекулярная термодиффузия или теплопроводность. В горячей части определенной среды молекулы более подвижны, они возбуждают своим действием соседние, в результате чего повышается температура.
- Конвекция. Данный процесс вызван движением жидкости. Поток жидкости непосредственно переносит начальную температуру из одной части пространства в другую. Если среда нагрета равномерно, конвективного теплового поток не будет даже при наличии движения.
- Излучение. Это передача внутреннего тепла в виде электромагнитных волн. Например, тепло от раскаленной печки или солнечная энергия.
Закон Паскаля
В случае, когда все массовые силы отсутствуют, т.е. $g = 0$, из этих формул получается, что $p = 0$. откуда следует, что $p = const$. Это решение носит в науке название закона Паскаля, который предполагает, что в покоящейся жидкости (газе) при отсутствии массовых и постоянных сил давление постоянно.
Уравнение состояния идеального газа $p = ρRT$ , отсюда можно найти плотность газа в зависимости от начальной температуры
Это обыкновенное дифференциальное уравнение первого порядка для внутреннего давления $p = z $. Оно решается согласно принципу разделения переменных:
Закон Паскаля в гидродинамике даёт формулу изменения давления с высотой, если известно точное распределение температуры по заданной величине. В частном случае, это действует в случае, если считать атмосферу изотермической, когда $Т = const$.
Эта формула доказывает, что давление в изотермической атмосфере постепенно убывает с высотой по экспоненциальному закону.
http://lfirmal.com/uravneniya-dvizheniya-v-forme-lamba/
http://spravochnick.ru/fizika/mehanika_sploshnyh_sred/uravneniya_gidrodinamiki/




