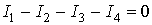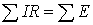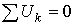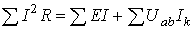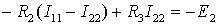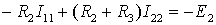Тема 4. баланс энергии ЭМП
Плотность ЭМ энергии и энергия, сосредоточенная в объеме. Мощность тепловых потерь и сторонних источников. Уравнение баланса для мгновенных значений мощности в дифференциальной и интегральной форме (теорема Умова – Пойнтинга). Физическая трактовка. Мощность, выходящая и входящая из объема через замкнутую поверхность. Вектор Пойнтинга. Мощность на входе приемника. Вектор Пойнтинга изотропного источника.
Средние за период значения энергетических характеристик гармонического ЭМП. Теорема Умова – Пойнтинга для комплексных мощностей. Комплексный вектор Пойнтинга. Уравнения баланса для активных и реактивных мощностей. Физическая трактовка. Скорость переноса энергии ЭМП.
Указания к теме
Поскольку ЭМ форма движения материи подчиняется закону сохранения энергии, непосредственно из системы уравнений Максвелла следует уравнение баланса энергии ЭМП (теорема Умова – Пойнтинга).
Необходимо учесть, что источником ЭМП является сторонняя сила, которую поддерживают посторонние по отношению к исследуемому полю источники. Сторонние источники не зависят от исследуемого поля и вводятся в основные уравнения ЭМП в виде дополнительных слагаемых.
При изучении этой темы важно уяснить физическое содержание каждого слагаемого уравнений баланса энергии как для некоторой области, так и для любой точки пространства. Необходимо рассмотреть различные виды балансов энергии (пассивный, нейтральный, активный) на примере LC-контура, чтобы уяснить связь между вектором Пойнтинга и движением энергии, ее излучением или поглощением, притоком или оттоком, скоростью движения энергии.
При изучении гармонических полей нужно обратить внимание на средние за период энергетические характеристики ЭМП, физическое содержание вещественной и мнимой частей вектора Пойнтинга.
Необходимо уяснить связь вектора Пойнтинга с мощностью, принимаемой антенной в дальней зоне приема, а также понять, почему плотность потока энергии изотропного источника убывает при удалении от него даже при отсутствии потерь в пространстве.
Основные сведения
После преобразования уравнений (2.5)–(2.8) [1–6] получаем дифференциальнуюформу теоремы Умова – Пойнтинга

После интегрирования по объему (4.1) и преобразований получаем
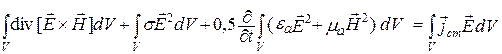
Каждое слагаемое в выражении (4.2) имеет размерность мощности
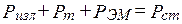
Уравнения (4.2)–(4.3) позволяют сформулировать теорему Умова –Пойнтинга: «Мощность стороннего источника в данном объеме расходуется на излучение, тепловые потери и изменение запаса энергии ЭМП» [1–3].
Мощность тепловых потерь (потерь проводимости) подчиняется закону Дж. Джоуля – Э. Ленца. Изменение запаса энергии имеет размерность мощности :

Вектор 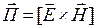
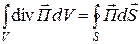
Вектор Пойнтинга указывает направление распространения излучения, а его модуль представляет собой плотность потока мощностиизлучения.
В комплексной форме уравнения (4.2) и (4.3) имеют вид [1]
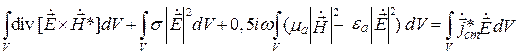
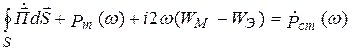
где 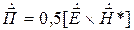
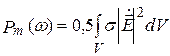
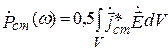
а 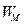
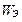
Выражение (4.6) – баланс комплексных мощностей в объеме V.
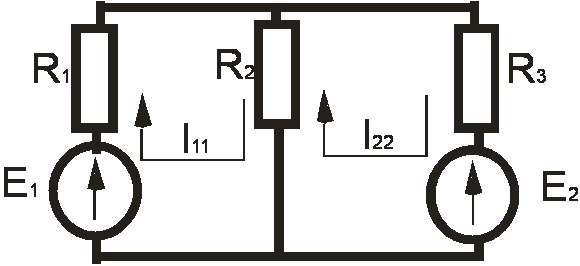
Рассмотрим баланс ЭМ энергии (4.3) в контуре, представляющем замкнутую электрическую цепь из элементов с сосредоточенными параметрами (рис. 4.1).

Выделим действительную и мнимую части уравнения (4.6)
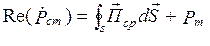
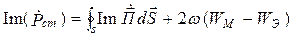
Действительная часть 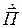
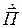
Из выражения (4.7) следует, что средняя мощность стороннего источника тратится на тепловые потери в объеме V и на создание ЭМП за пределами V.
Из выражения (4.8) следует, что реактивная мощность стороннего источника расходуется на создание потока реактивной мощности через границу V и на создание запаса реактивной энергии в объеме V. Реактивная мощность характеризует процесс обмена энергией между источником и цепью. При Pр > 0 энергия запасается в магнитном поле, а при Pр
Дата добавления: 2018-09-24 ; просмотров: 2086 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнение баланса энергии в локальной форме
Рассмотрим взаимные переходы форм энергии в некоторых типовых технологических устройствах.
Течение жидкости в трубопроводе. Учитывая отсутствие обмена энергией с внешней средой 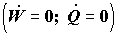
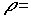
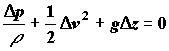
находящую многообразные приложения в технике.
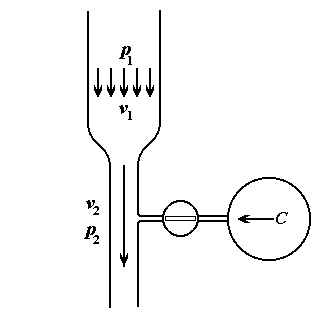
Рис.3.3. Схема действия водоструйного насоса; C– вакуумируемый сосуд.
Так, это уравнение характеризует изменение давления в потоке жидкости при сужении (расширении) трубопровода. Так как объемный расход несжимаемой жидкости через поперечное сечение трубы 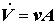
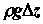
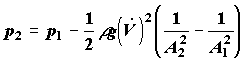
Последнее выражение объясняет действие водоструйного насоса (рис.3.3), показывая, что при заданных A1 и p1 могут быть достигнуты очень малые значения давления в струе p2 за счет, прежде всего, соответствующего уменьшения сечения струи A2, а также увеличения 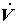
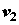
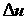
При 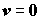
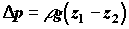
Еще один пример использования уравнения Бернулли – расчет скорости истечения жидкости из резервуара через свободное отверстие (например, в результате аварии) или через трубопровод в другой резервуар (рис. 3.4). В первом случае при одинаковом внешнем давлении 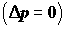
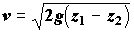
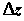
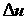
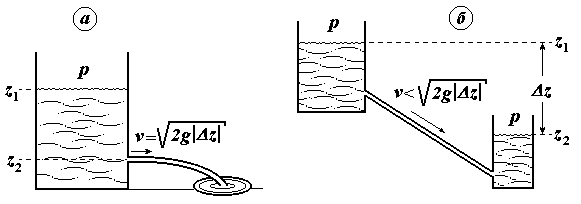
Гидротурбина и гидронасос. В гидротурбине происходит преобразование потенциальной энергии падающей воды через изменение ее кинетической энергии в механическую работу и с помощью электрогенератора – в электрическую работу;
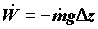
где 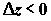
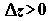
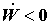
Теплообменный аппарат. В данном устройстве происходит нагревание (повышение энтальпии) одной движущейся среды за счет охлаждения (понижения энтальпии) другой путем теплообмена через разделяющие два потока перегородки.
Пусть массовый расход первого теплоносителя равен 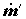
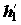
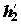
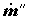
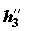
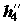
Обычно изменение механической энергии потоков в аппарате незначительно по сравнению с изменениями энтальпии, поэтому с большой точностью выполняется уравнение баланса
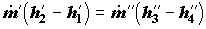
являющееся следствием (3.10) при 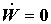
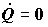
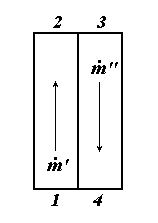
Рис.3.5. Схема противоточного теплообменного аппарата.
Адиабатный реактор. Как следует из уравнения (3.9), в адиабатном реакторе удельная энтальпия реакционной смеси сохраняется постоянной,
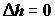
Если в реакторе протекает экзотермическая реакция, 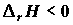
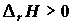
Газовая турбина и компрессор. В газовой турбине энтальпия разогретой смеси продуктов сгорания топлива с избытком воздуха трансформируется за счет адиабатического расширения в кинетическую энергию газов, которая в свою очередь преобразуется через вращение лопаток турбины в механическую работу; последняя с помощью генератора тока переводится в работу электрическую. В пренебрежении потерями теплоты в окружающую среду
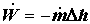
Этим же уравнением описывается работа газового компрессора в адиабатическом режиме (т.е. без внешнего охлаждения сжимаемой смеси); в этом случае электрическая или механическая работа расходуется на повышение энтальпии сжимаемого газа: 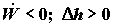
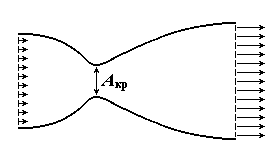
Реактивный двигатель. В реактивном двигателе раскаленные газы из камеры сгорания топлива направляются в сопло – сужающийся и затем расширяющийся канал рассчитанной конфигурации (рис. 3.6). В сужающейся части сопла газовая струя адиабатически расширяется и разгоняется до скорости, равной скорости звука, а в расширяющейся части ускоряется выше скорости звука. Газы приобретают высокую кинетическую энергию (и соответствующий импульс, который с противоположным знаком передается летательному аппарату) за счет результирующего уменьшения энтальпии исходной смеси топлива и окислителя:
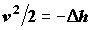
Рис.3.6. Схема сопла сверхзвукового реактивного двигателя;
Aкр– критическое сечение перехода через скорость звука.
Реакторы с внешним охлаждением или обогревом. В системах этого типа теплота, выделяемая в проточном реакторе в ходе экзотермической реакции, используется для нагревания внешнего теплоносителя, либо фазового превращения последнего. Например, промышленный реактор каталитического окисления аммиака включает в себя встроенный котел-утилизатор, в котором основная часть теплоты реакции утилизируется путем производства водяного пара. В противоположном случае проведения экзотермической реакции теплота подводится внешним теплоносителем. Преобразование химической и тепловой формы энергии в данных системах описывается тем же уравнением (3.13), что и обычный теплообмен.
К системам типа реактор-теплообменник по существу должны быть отнесены и многочисленные аппараты, в которых нагревание, фазовое или химическое превращение вещества производится за счет теплоты, выделяемой при сжигании в том же аппарате газообразного или жидкого топлива, как-то разного рода печи, паровые котлы, выпарные аппараты и т.п. (окисление топлива – наиболее широко используемая в технике и технологии химическая реакция).
Электронагревательные устройства. Нагревание рабочего вещества за счет джоулевой теплоты, выделяемой электронагревательными элементами, можно квалифицировать как потери электрической работы; баланс энергии в этом случае можно представить как
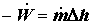
Электрохимический реактор. В электрохимических процессах происходит преобразование электрической, химической и тепловой форм энергии. В топливных элементах часть химической энергии исходных реагентов идет на выработку электрической энергии, а другая часть должна отводиться в виде теплоты внешним теплоносителем. Уравнение баланса энергии, суммарным образом характеризующее катодный и анодный процессы, может быть представлено в виде
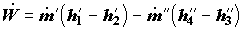
где 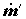
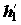
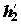
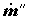
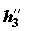
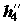
Во всех перечисленных выше примерах частные формы уравнений баланса потоков энергии выполняются с точностью до неучтенных в этих уравнениях и трудно измеряемых экспериментально потерь энергоресурсов. К последним относится рассеяние теплоты (также и холода) в окружающую среду через стенки аппаратуры и потери механической энергии на трение. Полноту целевого преобразования одной формы энергии в другую характеризует коэффициент преобразования энергии 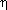
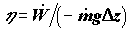
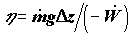
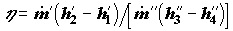
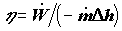
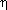
Коэффициент преобразования энергии, хотя и является важным количественным показателем эффективности функционирования технологической системы, не позволяет охарактеризовать процесс преобразования энергии с качественной стороны. На уровне балансов потоков энергии остается в стороне первостепенной важности вопрос о самой целесообразности перевода энергии из одной формы в другую. Этот вопрос может быть поставлен и решен лишь с привлечением второго начала термодинамики.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Уравнение баланса энергии в локальной форме

У73 Исследование оптимальных условий согласования на основе теории цепей постоянного тока: Учеб . п особие для студ. факультета нано – и биомедицинских технологий, обучающихся по направлению 550700 «Электроника и микроэлектроника» и специальностям 010600 «Физика твердого тела», 010400 «Физика», 014000 «Медицинская физика». 200100 «Материалы и компоненты твердотельной электроники», 014100 «Микроэлектроника и полупроводниковые приборы», 210104 «Микроэлектроника и твердотельная электроника», 202100 « Нанотехнология в электронике».
Учебное пособие представляет собой руководство к практическим занятиям по курсу «Теоретические основы радиоэлектроники». Содержит описание материала, знание которого необходимо при выполнении лабораторной работы по исследованию условий максимальной передачи мощности в линейных цепях постоянного тока.
Для студентов, обучающихся по направлению 550700 «Электроника и микроэлектроника» и специальностям 010600 «Физика твердого тела», 010400 «Физика», 014000 «Медицинская физика», 200100 «Материалы и компоненты твердотельной электроники», 014100 «Микроэлектроника и полупроводниковые приборы», 210104 «Микроэлектроника и твердотельная электроника», 202100 « Нанотехнология в электронике».
Рекомендуют к опубликованию:
Кафедра физики твердого тела физического факультета
Саратовского государственного университета, профессор, доктор физико-математических наук А. В. Скрипаль
УДК 621.315.592 ББК 22.379
ISBN 5-292-03602-1 © Горбатов С.С. , 2008
Саратовский государственный университет, 2008
§1. Законы Кир хгофа. Все электрические цепи подчиняются первому и второму законам (правилам) Кирхгофа.
Первый закон Кирхгофа можно сформулировать двояко:
1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю;
2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов.
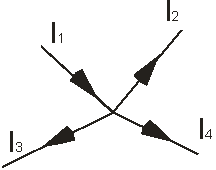
Так, применительно к рис. 1, если подтекающие к узлу токи считать положительными, а утекающие ‑ отрицательными, то согласно первой формулировке
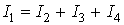
Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.
Если мысленно рассечь любую схему произвольной плоскостью и все находящееся по одну сторону от нее рассматривать как некоторый большой «узел», то алгебраическая сумма токов, входящих в этот «узел», будет равна нулю.
Второй закон Кирхгофа также можно сформулировать двояко:
1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме з . д. с. вдоль того же контура:
(в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:
Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.
§2. Соста вление уравнений для расчета токов в схемах с помощью законов Кирхгофа.
Законы Кирхгофа используют для нахождения токов в ветвях схемы. Обозначим число всех ветвей схемы в, число ветвей, содержащих источники тока, — вит и число узлов — у. В каждой ветви схемы течет свой ток. Так как токи в ветвях с источниками тока известны, то число неизвестных токов равняется в — в ит . Перед тем как составлять уравнения, необходимо произвольно выбрать:
а) положительные направления токов в ветвях и обозначить их на схеме;
б) положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа.
С целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми, например, по часовой стрелке.
Чтобы получить линейно независимые уравнения, по первому закону Кирхгофа составляют число уравнений, равное числу узлов без единицы, т. е. 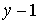
Уравнение для последнего 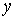
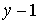
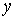
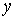
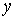
По второму закону Кирхгофа составляют число уравнений, равное числу ветвей без источников тока (в — в ит ), за вычетом уравнений, составленных по первому закону Кирхгофа, т. е. 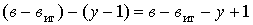
Составляя уравнения по второму закону Кирхгофа, следует охватить все ветви схемы, исключая лишь ветви с источниками тока. При записи линейно независимых уравнений по второму закону Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону Кирхгофа. Такие контуры условимся называть независимыми.
Требование, чтобы в каждый новый контур входила хотя бы одна новая ветвь, является достаточным, но не необходимым условием, а потому его не всегда выполняют. В таких случаях часть уравнений по второму закону Кирхгофа составляют для контуров, все ветви которых уже вошли в предыдущие контуры.
§3. Энергетический баланс в электрических цепях.
При протекании токов по сопротивлениям в последних выделяется тепло. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источниками питания.
Если направление тока 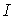
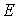
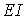
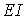
Если же направление тока 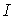
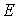
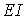
Уравнение энергетического баланса при питании только от источников э. д. с. имеет вид
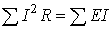
Когда схема питается не только от источников э. д. с., но и от источников тока, т. е. к отдельным узлам схемы подтекают и от них утекают токи источников тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Допустим, что к узлу а схемы подтекает ток 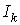
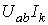
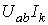
Для практических расчетов электрических цепей разработаны методы, более экономичные в смысле затраты времени и труда, чем метод расчета цепей по законам Кирхгофа. Рассмотрим эти методы.
§ 4 . М етод пропорциональных величин.
Согласно методу пропорциональных величин, в самой удаленной от источника э. д. с. ветви схемы (исходной ветви) произвольно задаемся некоторым током, например током в 1 А. Далее, продвигаясь к входным зажимам тп , находим токи в ветвях и напряжения на различных участках схемы. В результате расчета получим значение напряжения 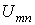
Так как найденное значение напряжения 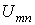
Метод пропорциональных величин, если рассматривать его обособленно от других методов, применим для расчета цепей, состоящих только из последовательно и параллельно соединенных сопротивлений и при наличии в схеме одного источника.
Однако этот метод можно использовать и совместно с другими методами (преобразование треугольника в звезду, метод наложения и т. п.), которые рассмотрены далее.
§ 5 . Метод контурных токов.
При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего определяют токи ветвей через контурные токи.
Таким образом, метод контурных токов можно определить как метод расчета, в котором за искомые принимают контурные токи. Число неизвестных в этом методе равно числу уравнений, которые необходимо было бы составить для схемы по второму закону Кирхгофа.
Следовательно, метод контурных токов более экономен при вычислительной работе, чем метод на основе законов Кирхгофа (в нем меньшее число уравнений).
Вывод основных расчетных уравнений проведем применительно к схеме рис. 3, в которой два независимых контура. Положим, что в левом контуре по часовой стрелке течет контурный ток 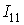
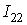
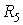
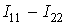
Для первого контура
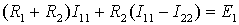
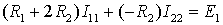
Для второго контура
В уравнении (б) множитель при токе 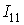
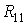
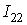
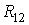
Перепишем эти уравнения следующим образом:
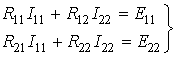
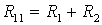
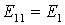
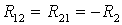
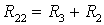
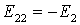
где 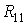
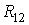
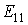
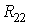
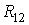
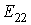
В общем случае можно сказать, что сопротивление смежной ветви между k и т контурами 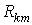
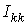
Если в схеме больше двух контуров, например три, то система уравнений выглядит следующим образом:
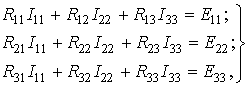
или в матричной форме:
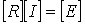
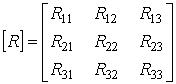
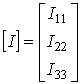
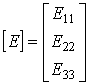
Рекомендуется для единообразия в знаках сопротивлений с разными индексами все контурные токи направлять в одну и ту же сторону, например все по часовой стрелке.
Если в результате решения системы уравнений какой-либо контурный ток окажется отрицательным, то это означает, что в действительности направление контурного тока обратно принятому за положительное.
В ветвях, не являющихся смежными между соседними контурами (например, в ветви с сопротивлениями 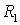
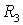
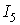
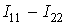
Если в электрической цепи имеется п независимых контуров, то число уравнений тоже равно п.
Общее решение системы п уравнений относительно тока 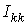
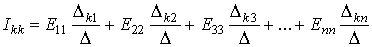

Алгебраическое дополнение 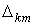

Если из левого верхнего угла определителя провести диагональ в его правый нижний угол (главная диагональ) и учесть, что 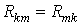
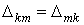
Формула (2) в ряде параграфов используется в качестве исходной при рассмотрении таких важных вопросов теории линейных электрических цепей, как определение входных и взаимных проводимостей ветвей, принцип взаимности, метод наложения и линейные соотношения в электрических цепях.
Составлению уравнений по методу контурных токов для схем с источниками тока присущи некоторые особенности. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источниками э.д.с . и сопротивлениями, и что эти токи известны и равны токам соответствующих источников тока. Уравнения составляют лишь для контуров с неизвестными контурными токами.
§ 6. Принцип наложения и метод наложения.
Чтобы составить общее выражение для тока в k -ветви сложной схемы, составим уравнения по методу контурных токов, выбрав контуры так, чтобы k — ветвь входила только в один k -контур (это всегда возможно).
Тогда ток в k -ветви будет равен контурному току 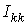
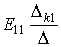
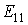
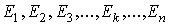
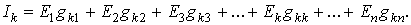
Если контуры выбраны таким образом, что какая-либо из э.д.с , например 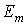
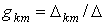
Уравнение (4) выражает собой принцип наложения.
Принцип наложения формулируется следующим образом: ток в k -ветви равен алгебраической сумме токов, вызываемых каждой из э.д.с . схемы в отдельности. Этот принцип справедлив для всех линейных электрических цепей.
Принцип наложения используется в методе расчета, получившем название метода наложения.
При расчете цепей по методу наложения поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из э.д.с , мысленно удаляя остальные из схемы, но оставляя в схеме внутренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения частичных токов. Заметим, что методом наложения нельзя пользоваться для подсчета выделяемых в сопротивлениях мощностей как суммы мощностей от частичных токов, поскольку мощность является квадратичной функцией тока ( 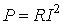
Так, если через некоторое сопротивление 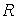
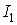
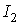
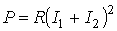
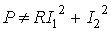
Уравнение баланса мощности 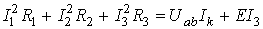
Пр актическая часть
Электрическая схема находится в файле «Схема 7». Она представляет собой линейный четырехполюсник со сложной внутренней структурой. В схеме имеется источник напряжения, подключенный на входе и приборы, измеряющие ток и напряжение в ветви, содержащей выходное сопротивление.
В файле «Схема 7» ( сохранить файл на компьютер и открыть, используя программу Electronic Workbench 512 ) изменяя сопротивление с номиналом 20 Ом в пределах от 20 Ом до 10000 Ом нарисовать график функции изменения мощности в данном диапазоне сопротивлений, используя показания вольтметра и амперметра, умножая ток на напряжение. Зависимость произведения тока на напряжение и является искомой зависимостью мощности, выделяемой в сопротивлении нагрузки. Экстремум данной функции достигается при сопротивлении, равном выходному сопротивлению исходного линейного четырехполюсника со сложной внутренней структурой. Его необходимо найти.
Изменить номиналы входящих в схему сопротивлений.
Повторить порядок выполнения задания 1.
1. Гоноровский И.С. Радиотехнические цепи и сигналы. Часть1.Сигналы. Линейные системы с постоянными и переменными параметрами. М. Советское радио. 1968г. 408с. ил
2. Атабеков Г. И. Теоретические основы электротехники, ч. I. Линейные электрические цепи. — М.: Энергия, 1978.
3. Белецкий А. Ф. Теория линейных электрических цепей. — М.: Радио и связь, 1986.
4. Теоретические основы электротехники, т. 1. Основы теории линейных цепей / Под ред. П. А. Ионкина . — М.: Высшая школа, 1976.
5. Теория линейных электрических цепей/Под ред. И. Г. Кляцкина . — М.: Высшая школа, 1973.
6. Лосев А. К. Линейные радиотехнические цепи.— М.: Высшая школа, 1971.
7. Матханов П. Н. Основы анализа электрических цепей. Линейные цепи. — М.: Высшая школа, 1981.
http://www.chem.msu.ru/rus/teaching/safonov/part010.html
http://elibrary.sgu.ru/uch_lit/%D0%9F%D0%BE%D1%81%D0%BE%D0%B1%D0%B8%D0%B5%2011.htm