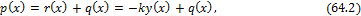Уравнение балки на упругом основании

Уравнение балки на упругом основании

В этом ИДЗ мы проведём полный расчёт балки на упругом основании (рис.1), находящейся под действием произвольной системы изгибающих моментов, сосредоточенных сил и равномерно распределённых нагрузок, расположенных в вертикальной плоскости.

Это пособие предназначено для студентов, изучающих курс сопротивления материалов. Прямо из этого пособия Вы можете посчитать своё ИДЗ, даже если у Вас нет на компьютере MATLAB. Если же у Вас есть MATLAB, перейдите на эту страницу: там у Вас есть возможность вмешаться в сценарий (программу) вычислений. Здесь же выполнение ИДЗ проводится по стандартному сценарию, который обычно используется в вузах при изучении курса сопромата.

Для правильной работы с этой страницей Ваш браузер должен поддерживать сценарии Java Script. Включите их.

Данное пособие позволит вам упростить выполнение ИДЗ. Как и любой помощник, оно не избавляет вас от необходимости думать. Используя это пособие, вы получите техническую помощь, избавитесь от досадных ошибок вычислений, но понимать существо проблемы вы всё равно должны. Но не пугайтесь: если вы смогли найти эту страницу в Internet, то разобраться в выполнении этого задания сможете наверняка.

Граничные условия на каждом краю могут быть одного из трёх типов:

Выберем систему координат так, как показано на рис.2.

Начало координат O поместим на левом краю, ось Oz направим вдоль оси балки, а оси Ox и Oy − вдоль главных центральных осей инерции. Все силовые факторы считаем действующими в плоскости yOz, как показано на рис.2.

Будем использовать правило знаков плюс-плюс-плюс-плюс:

• угол поворота сечения θ есть производная от вертикального перемещения w, взятая со знаком плюс;
• изгибающий момент в сечении M есть производная от угла поворота θ, умноженного на EJ_x, взятая со знаком плюс;
• перерезывающая сила в сечении Q есть производная от изгибающего момента M, взятая со знаком плюс;
• распределённая нагрузка q есть производная от перерезывающей силы Q, взятая со знаком плюс:

В соответствии с [1] выберем положительное направление прогиба w(z) вверх, в сторону положительного направления оси Oy, а отрицательное − вниз (рис.3).

Тогда положительные значения углов поворота θ(z) будут соответствовать возрастанию прогиба w(z), а отрицательные − убыванию (рис.4).

Изгибающий момент − это вторая производная от прогиба (с точностью до положительного множителя) и первая производная от угла поворота θ(z) (опять-таки с точностью до положительного множителя); поэтому положительное значение момента M(z) соответствует увеличению угла поворота θ(z), т.е. изгибу балочки выпуклостью вниз, а отрицательный M(z) − изгибу выпуклостью вверх (рис.5).

При построении эпюр мы будем разрезать балку в данном сечении z, отбрасывать левую часть и заменять её эквивалентной системой сил и моментов. Положительное значение M(z) (выпуклостью вниз) при этом даст момент, направленный по часовой стрелке (рис.6).

Поэтому в исходных данных сосредоточенные моменты будем задавать положительными, если они направлены по часовой стрелке.

Теперь рассмотрим правило знаков для перерезывающих сил. В соответствии с (3) положительной будем считать такую силу Q(z), которая соответствует возрастанию изгибающего момента M(z) при увеличении z. Наглядно представить себе увеличение вогнутости трудно, поэтому применим другое правило для определения знака Q(z). Заменим отрезанную левую часть такой силой, которая соответствует увеличению M(z) (рис.7). Т.к. момент равен произведению силы на плечо, то положительное значение сосредоточенной силы соответствует направлению её вверх. Такая сила стремится повернуть элемент балки по часовой стрелке.

И, наконец, выведем правило знаков для распределённой нагрузки q(z). Положительная q(z) соответствует возрастанию перерезывающей силы Q(z). На рис.8 показано положительное направление q(z): вверх. Именно такое направление q(z) соответствует возрастанию Q(z).

Итак, подытожим всё вышесказанное. При задании исходных данных будем считать:

• распределённую нагрузку q положительной, если она направлена вверх;
• сосредоточенную нагрузку F положительной, если она направлена вверх;
• сосредоточенный момент M положительным, если он направлен по часовой стрелке.

При построении эпюр будем руководствоваться формулами (1-4). Считаем:

• перемещение w положительным, если оно направлено вверх;
• положительный угол поворота θ соответствует возрастанию w;
• положительный изгибающий момент M соответствует возрастанию θ;
• положительная перерезывающая сила Q соответствует возрастанию M;
• положительная распределённая нагрузка q соответствует возрастанию Q.

Краткие теоретические сведения

В соответствии с [1] выведем дифференциальное уравнение изогнутой оси балки. Это уравнение имеет вид: вторая производная от изгибающего момента EJ_xw IV (z)) равна сумме всех распределённых нагрузок в данном сечении на единицу длины. Такими нагрузками будут внешние силовые факторы и реакция упругого основания. Коэффициент жёсткости упругого основания c − это сила, с которой действует упругое основание на единицу площади нижней поверхности балки при единичном прогибе основания. Поэтому размерность c будет Н/м 3 . Если обозначить ширину нижней поверхности балки через b, то

− это сила, с которой действует упругое основание на единицу длины балки при единичном прогибе. Размерность α будет Н/м 2 . Сила реакции упругого основания на единицу длины тогда будет равна αw, и направлена в сторону, противоположную прогибу. дифференциальное уравнение изогнутой оси балки на упругом основании имеет вид:

где q(z) − обобщённая внешняя нагрузка, учитывающая все силы и моменты. Дифференциальное уравнение (6) дополняется 4 граничными условиями: по 2 на левом и правом концах, в зависимости от условий закрепления.

Решение уравнения (6) удобно записывать через функции Крылова:

Эти функции обладают свойством:

Если ввести в рассмотрение приведённую длину:

то общее решение дифференциального уравнения (6) записывается в виде:

Здесь EJ_xw₀ − прогиб в левом сечении (с точностью до множителя EJ_x), EJ_xθ₀ − угол поворота левого сечения (также с точностью до множителя EJ_x), M₀ и Q₀ − изгибающий момент и перерезывающая сила в левом сечении. Во второй строке в 1-й и 2-й суммах a_k − точка приложения сосредоточенного момента или силы; в 3-й и 4-й суммах a_k − начало приложения распределённой нагрузки, в b_k − конец. В каждой из сумм суммирование проводится по всем силовым факторам, расположенным слева от текущего сечения.

Неизвестные начальные параметры EJ_xw₀, EJ_xθ₀, M₀ и Q₀ находятся из граничных условий. Всего таких условий 4: по 2 на каждом краю балочки. Составив соответствующую систему уравнений и решив её, мы найдём эти начальные параметры.

Далее последовательное дифференцирование выражения (10) даёт угол поворота:

и перерезывающую силу:

По выражениям (10-13) можно построить эпюры.

Ввод исходных данных

В данном методическом пособии можно использовать такие нагрузки:

• сосредоточенный момент;
• сосредоточенная сила;
• равномерно распределённая нагрузка.

На концах можно задавать такие условия закрепления:

• жёсткая заделка;
• свободное опирание (шарнир);
• свободный край.

Если в вашем вузе преподаватели задают студентам другие виды нагружения (распределённые моменты, линейную нагрузку и т.п.), промежуточные опоры или другие граничные условия (например, упругая заделка), − напишите мне, и мы вместе доработаем это пособие.

Исходными данными для выполнения этого ИДЗ являются длина балочки L, граничные условия, данные по двутавровому сечению, физические характеристики материала балки и упругого основания, и нагрузка на неё: значения M, F, q и точки (интервалы) их приложения. Заметим, что здесь сечение нужно задать заранее, его данные входят в коэффициенты дифференциального уравнения (6) через множитель α (5). Задайте исходные данные в нижеприведенных областях ввода.

Проверьте, правильно ли вы задали исходные данные. Если да, то идём дальше.

Нахождение начальных параметров

Наша балочка является статически неопределимой: неизвестные начальные параметры не могут быть найдены из уравнений статики. Они находятся из граничных условий. Для нахождения этих 4 неизвестных начальных параметров у нас есть столько же уравнений: по 2 каких-либо параметра на каждом краю балочки равны нулю − всего 4 уравнения.

В зависимости от вида граничных условий будут равны нулю:

1. в жёсткой заделке − перемещение и угол поворота;
2. при шарнирном закреплении − перемещение и изгибающий момент;
3. на свободном краю − изгибающий момент и перерезывающая сила.

Вначале найдём точки переключения аналитических выражений в формулах (10-13). Это будут: начало и конец балочки и точки приложения всех силовых факторов (для распределённой нагрузки q берём и начало, и конец приложения). Запишем также характеристики выбранного двутаврового сечения и другие необходимые для расчёта данные.

Запишем теперь систему уравнений для определения начальных параметров и решим её. Первые 2 уравнения − это граничные условия на правом конце балочки, а 3-е и 4-е уравнения − на правом конце.

Построение эпюр

Теперь, когда мы вычислили все необходимые данные для формул (10-13), строим эпюры перемещений, углов поворота, изгибающих моментов и перерезывающих сил. Вначале записываем аналитические выражения на каждом участке, а затем строим графики. Перемещения и углы поворота строим в натуральном масштабе.

Подбор сечения по условиям прочности

Найдём максимальный (по модулю) изгибающий момент M_max и сечение, в котором он достигается (опасное сечение).

находим максимальное нормальное напряжение в опасном сечении. Проверим теперь касательные напряжения. В каждом сечении они подсчитываются по формуле Журавского:

Как правило, касательные напряжения значительно меньше нормальных в одном и том же сечении, к тому же они достигаются на разных волокнах: нормальные − на крайних, а касательные − в середине сечения. Поэтому опасными является обычно нормальные напряжения.

Нарисуем распределение нормальных и касательных напряжений по сечению. Нормальные напряжения распределены линейно, а касательные − по параболе. Мы строим эпюру распределения касательных напряжений приближённо: заменяем двутавр набором прямоугольников. Вычисляем по формуле (15) напряжения в крайних волокнах тонкой вертикальной стойки и во внутренних волокнах широкой горизонтальной полки. На стойке строим параболу, а на короткой полке ограничимся прямолинейным отрезком. Рисуем сечение , распределение нормальных и касательных напряжений в опасном сечении (там, где достигается M_max), и распределение касательных напряжений в том сечении, где достигается Q_max.

Если максимальное напряжение не достигают допускаемого, можно подобрать более лёгкий двутавровый профиль из списка. А если, наоборот, превышает, выберите более тяжёлый.

Что делать дальше

Возможно, Вы захотите распечатать результаты. Если перебросить содержимое, например, в то формулы и графики исказятся, они сделаны не в виде рисунков, а в виде встроенных объектов. Поэтому лучше распечатывать страницу непосредственно из обозревателя.

Уравнение балки на упругом основании

Общие понятия.

К числу статически неопределимых балок может быть отнесена балка на упругом основании. Так называется балка, опирающаяся по всей своей длине (Рис.1) на упругое основание, оказывающее в каждой точке на балку реакцию, пропорциональную у — прогибу балки в этой точке. Коэффициент пропорциональности обозначается буквой k.

Введение предположения о пропорциональности реакций прогибу является приближением, хотя и достаточно близким к действительным условиям.

Рис.1. Расчетная схема балки на упругом основании.

Предложение ввести в расчет коэффициент пропорциональности к, именуемый «коэффициентом постели», было впервые сделано русским академиком Николаем Ивановичем Фуссом в 1801 году. Принимая это предположение, получаем, что интенсивность реакции основания в каждой точке сила равна ky и измеряется в единицах силы и длины; размерность коэффициента k при этом будет сила и квадрат длины. Будем считать, что основание оказывает реакцию при прогибах балки как вниз, так и вверх.

На практике задачи о расчете балки на упругом основании встречаются в железнодорожном деле (рельс, шпала), в строительстве — фундаменты различных сооружений, передающие нагрузку на грунт.

Статически неопределимой такая балка будет потому, что условие статики— сумма нагрузок равна всей реакции основания — не дает возможности установить распределение этой реакции по длине балки, а значит, вычислить изгибающие моменты и поперечные силы.

Интенсивность реакции в каждой точке связана с прогибами балки. Поэтому для решения задачи необходимо найти сначала уравнение изогнутой оси , а уже затем формулы для вычисления изгибающего момента и поперечной силы. Ход решения оказывается обратным обычному.

Найдем уравнение изогнутой оси для балки постоянного сечения, лежащей на упругом основании и нагруженной сосредоточенными силами . (Рис.1). Начало координат возьмем в любой точке, ось х направим вправо, ось у вертикально вверх. Направление нагрузок вверх будем считать положительным. Напишем обычное дифференциальное уравнение изгиба

Так как М(х) нам неизвестен, то постараемся связать прогибы непосредственно с нагрузкой, для этого дифференцируем дважды предыдущее уравнение:

где q(x)—интенсивность сплошной нагрузки, действующей на балку в сечении с абсциссой х.

Сплошной нагрузкой для нашей балки является лишь реакция упругого основания. Интенсивность ей пропорциональна прогибам; эта нагрузка направлена вверх, т. е. положительна, когда прогибы идут вниз, т. е. отрицательны, и наоборот. Таким образом, эта нагрузка имеет знак, обратный знаку прогибов:

Если обозначить , то общий интеграл уравнения (25.3) имеет вид: (25.4)

Постоянные А, В, С, D должны быть определены в каждом частном случае нагрузки и длины балки. Величина имеет измерение обратное длине.

Расчет бесконечно длинной балки на упругом основании, загруженной одной силой Р.

Наиболее просто решается задача об изгибе бесконечно длинной балки, нагруженной одной сосредоточенной силой (Рис.2). Помимо непосредственного практического значения решение этой задачи позволит путем последовательных приближений рассчитывать и балки конечной длины.

Рис.2. Расчетная схема балки бесконечной длины.

Начало координат расположим в точке приложения силы Р. Определим постоянные А, В, С и D. Так как вся реакция основания, равная силе Р должна быть конечной величиной, то прогибы балки в точках, бесконечно удаленных от точки приложения силы, должны обращаться в нуль:

При бесконечно больших значениях х два вторых слагаемых в правой части формулы (4) обращаются в нуль благодаря множителю , два же первых могут обратиться в нуль лишь при

и

Далее, по симметрии нагрузки и реакции основания, касательная к изогнутой оси в точке приложения силы должна идти параллельно оси абсцисс:

Дифференцируя (6), получаем:

Подставляя в это выражение и приравнивая результат нулю, находим:

таким образом, уравнения будут:

Для определения последней постоянной С имеем еще одно уравнение: нам известна величина поперечной силы в начале координат.

Разрезав балку сечением в точке О справа от силы Р и рассматривая правую часть балки, видим, что поперечная сита в этом сечении равна реакции основания, действующей на правую половину балки со знаком минус; так как реакция направлена вверх (для правой половины) и вся реакция основания равна Р, значит, поперечная сила в сечении при х = 0 равна

Но, с другой стороны

Вычисляем, пользуясь (8), и :

Подставляя (12) в (10) и приравнивая х нулю, получаем:

и

Теперь значения у и ее производных получают вид

Таким образом, напряженное состояние и деформации балки на упругом основании всецело определяются нагрузкой и коэффициентом , зависящим от соотношения жесткостей балки и упругого основания.

Уравнение балки на упругом основании

64. Балка на упругом основании

64.1. Дифференциальное уравнение оси изогнутой балки,

лежащей на сплошном упругом основании

В инженерной практике часто встречаются балочные элементы конструкций, лежащие на сплошном упругом основании . К таким конструкциям могут быть отнесены шпалы железнодорожного пути, ленточные фундаменты зданий, фундаменты плотин, опирающиеся на грунты, разного рода трубопроводы, уложенные на грунт или внутрь его и др. Кроме того, к таким конструкциям относятся также и рельсы, у которых число опор бесконечно вели­ко, а расстояние между ними мало по сравнению с длиной.

В машиностроении и различных других областях техники для многих конструкций в эксплуатационном режиме, находящихся в условиях сплошного контакта с другими изделиями, можно применить расчетную схему балки на упругом основании.

При расчетах таких элементов предполагается, что грунт обладает упругими свойствами и его деформация пропорциональна приложенной нагрузке. Кроме этой основной предпосылки, при расчете балок на упругом основании принимаются и другие допущения:

— трение между основанием и балкой отсутствует;

— между опорной поверхностью балки и основанием имеется неразрывная связь, вследствие чего в основании могут возникнуть растягивающие усилия;

— упругое основание по всей длине балки однородно и ширина постели балки постоянная;

Расчет балки на упругом основании в строгой постановке сводится к решению контактной задачи между конструкцией и осно­ванием. Сложность решения контактных задач в строгой постановке общеизвестна. Поэтому для решения инженерных задач, связанных с расчетом балки применяются приближенные подходы, суть которых заключается в следующем.

Предварительно устанавливается зависимость между реактивным отпором и осадкой поверхности основания. Одной из наиболее распространенных гипотез является гипотеза о пропорциональной зависимости между реакцией и осадкой — гипотеза Винклеровского основания.

На рис.64.1 показана деформация балки от внешней нагрузки, распределенной по произвольному закону. Реакция со стороны ос­нования в произвольной точке, при соблюдении условий проскальзывания на контактной поверхности между подошвой балки и основанием, принимается пропорциональной прогибу:

r x =- k ∙ y x , ( 64 .1)

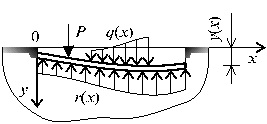
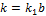где r( x) — реакция основания, приходящаяся на единицу длины балки, (Н/м); y( x) — просадка основания; k = k 1 b ; b — ширина подошвы балки; k₁ — коэффициент, характеризующий жесткость ос­нования и называемый коэффициентом податливости ос­нования или коэффициентом постели, [Па/м].

Этот коэффициент представляет собой отпор основания, при­ходящийся на 1 м 2 площади при просадке, равной единице. Знак минус в выражении (64.1) означает, что реакция противоположна направлению просадки.

Значения коэффициента постели k₁ для некоторых грунтовых и скальных оснований приведены в таблице 64.1.

Балка, лежащая на сплошном упругом основании, представляет собой статически неопределимую систему, так как одного условия равновесия – равенства внешней нагрузки всей общей реакции основания – недостаточно для установления закона распределения этой реакции по длине балки и для определения усилий в сечениях. Интенсивность реакции в каждой точке связана с прогибом балки, поэтому для решения задачи необходимо найти уравнение изогнутой оси балки, затем по этому уравнению определить закон распределения реактивных сил.

Таким образом, со стороны основания на балку действует сплошная распределенная нагрузка интенсивностью r( x). Суммар­ная интенсивность распределенной нагрузки, приложенной к балке при произвольном значении x определяется :

p x = r x + q x =- ky x + q x , ( 64 .2)

где q( x) — приложенная к балке, заданная распределенная нагрузка (например, вес погонной длины балки).

Таблица 64 .1. Значения коэффициента постели k₁ для различных грунтов