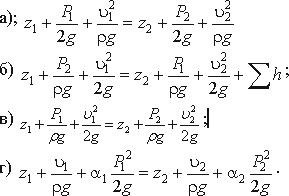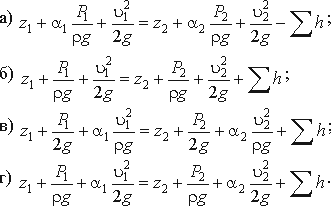Вопрос № 17. Уравнение Бернулли для идеальной жидкости.
Читайте также:
|
 |
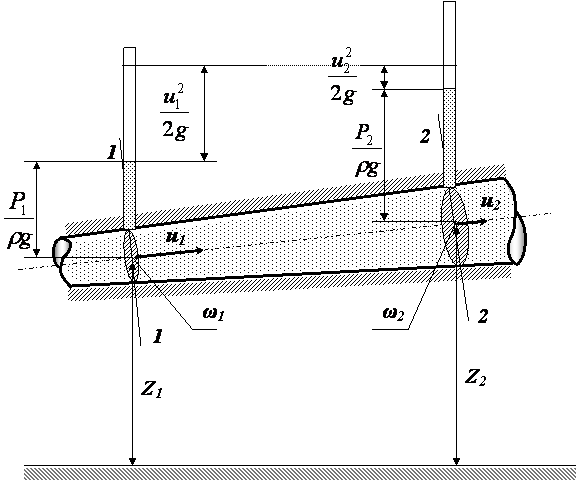
Все слагаемые уравнения Бернулли имеют размерность длины и их можно изобразить графически.
Значения 


Из уравнения Бернулли для струйки невязкой жидкости (и графика) следует, что гидродинамический напор по длине струйки постоянен.
Выше было получено уравнение Бернулли с использованием
энергетических характеристик жидкости. Суммарной энергетической характеристикой жидкости является её гидродинамический напор.
С физической точки зрения это отношение величины механической энергии к величине веса жидкости, которая этой энергией обладает. Таким образом, гидродинамический напор нужно понимать как энергию единицы веса жидкости. И для идеальной жидкости эта величина постоянна по длине. Таким образом, физический смысл уравнения Бернулли это закон сохранения энергии для движущейся жидкости.
Здесь с энергетической точки зрения (в единицах энергии, Дж/кг) gz — удельная потенциальная энергия положения; Р/r — удельная потенциальная энергия давления; gz + Р/r — удельная потенциальная энергия; u 2 /2 — удельная кинетическая энергия; и — скорость элементарной струйки идеальной жидкости.
Умножив все члены уравнения на удельный вес жидкости g, получим
gz — весовое давление, Па; P — гидродинамическое давление, Па; rи 2 /2 — динамическое давление Па; gH — полное давление, Па
Вопрос №19. Два режима движения жидкости. Число Рейнольдса.
В 1883 году английским учёным Осборном Рейнольдсом (1842-1912 гг.) было установлено, что критерием режима течения жидкости является безразмерная величина, представляющая собой отношение произведения средней скорости потока и линейного размера, характерного для живого сечения, к кинематической вязкости жидкости n.
Критерий режима течения жидкости называется числом Рейнольдса.
При течении жидкости в круглых трубах за характерный размер l объёма принимается внутренний диаметр трубы D, тогда
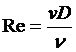
Пример. Установить, какой режим будет в трубе диаметра D=20 см, если средняя скорость 

Розв`язування. 
Опытные данные Рейнольдса показывают наличие трёх областей:
АК — ламинарной, ВК — переходной или неустойчивый, ВС — турбулентной ( рис. 41 ).
Точки К и В называются критическими точками, точками, в которых происходит смена режима течения.
Ниже точки К режим всегда ламинарный, выше точки В — турбулентный.
В зависимости от изменения скорости от малых значений к большим и от больших к малым ламинарный режим удерживается до точки В при увеличении скорости, или при уменьшении до точки К.
Значение числа Рейнольдса, соответствующее нижней критической точке К, называется нижним критическим числом Рейнольдса, число Re соответствует верхней критической точке — верхним критическим числом Рейнольдса.
Нижнее число Рейнольдса Re= 956.
Переход к турбулентному режиму зависит (помимо скорости течения, вязкости и характерного размера) от ряда факторов — источников питания трубопровода, шероховатости труб, местных сопротивлений и т.д. Верхнее число Рейнольдса обычно принимают равным Re= 5000.
На практике ламинарный режим встречается
1) при движении очень вязких жидкостей,
2) при движении жидкости в тонких ( капилярных ) трубах,
3) при движении воды в грунтах.
Турбулентный режим наблюдается значительно чаще: при движении в каналах, трубах и т.д.
Профиль скорости при ламинарном и турбулентном режиме течения
При ламинарном режиме жидкости движение как бы разделяется на бесконечно большое число тонких коаксиально расположенных относительно оси трубопровода слоёв.
Распределение скоростей по сечению имеет вид параболы. Скорость у стены равна нулю. При удалении от стенки скорости возрастают и достигают максимума на оси трубы.
Определим закон распределения скорости. Выделим объём жидкости в виде цилиндра радиуса r и длиной l и составим уравнение равновесия ( рис. 42 )

Движение установившееся, скорости на одном радиусе одинаковы.

С учётом гидравлического уклона


Проинтегрируем по сечению трубы, учитывая, что при r=r0 и u=0, получим закон распределения скоростей в сечении

Максимум скорости при r=0

Определим расход жидкости через трубу


Соотношение между максимальной и средней скоростью

Турбулентный режим движения жидкости характеризуется беспорядочным движением частиц. При этом режиме частицы жидкости движутся по произвольным траекториям и с различной скоростью. Скорость изменяется по величине и направлению около среднего значения.
Такое изменение скорости называется пульсацией скорости. Среднюю по времени скорость называют осреднённой скоростью. Связь между осреднённой и мгновенной скоростью может быть выражена зависимостью

где Т — период наблюдения.
Распределение скоростей течения в этом случае выглядит иначе, чем при ламинарном режиме( рис. 43 ).
 Рис. 43 1-ламинарная плёнка, 2-переходный слой, 3-ядро турбулентного потока Рис. 43 1-ламинарная плёнка, 2-переходный слой, 3-ядро турбулентного потока | В ламинарной пленке и переходном слое скорости течения изменяются так же, как при ламинарном режиме течения. В переходной зоне зарождаются вихри, обусловленные увеличением скорости движения, влиянием выступов шероховатости. |
Если выступы шероховатости меньше толщины ламинарной пленки, стенка будет гидравлически гладкой. При величине выступов выше толщины ламинарной пленки, неровности стенок будут увеличивать беспорядочность движения и стенка будет гидравлически шероховатой.
Возникающие в пограничном слое вихри проникают в центральную часть потока и образуют ядро турбулентного течения. В ядре потока происходит интенсивное и непрерывное перемешивание частиц жидкости.
Для описания профиля скорости в ядре течения турбулентного состояния используется логарифмический закон распределения скоростей

Величина коэффициента трения зависит от режима течения жидкости.
Опытами было установлено, что при течении жидкости возможны два режима: ламинарный и турбулентный.
 Рис. 39 Рис. 39 | При ламинарном режиме жидкость течёт слоями, не перемешиваясь ( рис. 39 ). |
 Рис. 40 Рис. 40 | При турбулентном частицы жидкости интенсивно перемешиваются ( рис. 40 ). |
Ламинарное и турбулентное течение жидкости можно наблюдать в стеклянной трубе В ( рис. 39, 40 ).
Питание трубы производится из бака, а скорость течения регулируется краном С. Для наблюдения за характером движения жидкости по тонкой трубке в трубу В подводится подкрашенная жидкость такой же плотности, как и движущаяся жидкость (например, чернило).
При малых скоростях в трубе В струйка продолжает двигаться, не перемешиваясь с остальной жидкостью, что указывает на ламинарный режим течения.
При больших скоростях в трубе струйка очень сильно перемешивается со всей жидкостью, что указывает на турбулентный режим.
Дата добавления: 2015-04-18 ; просмотров: 225 ; Нарушение авторских прав
Уравнение бернулли для идеальной жидкости имеет вид тест
3.1. Площадь поперечного сечения потока, перпендикулярная направлению движения называется
а) открытым сечением;
б) живым сечением;
в) полным сечением;
г) площадь расхода.
3.2. Часть периметра живого сечения, ограниченная твердыми стенками называется
а) мокрый периметр;
б) периметр контакта;
в) смоченный периметр;
г) гидравлический периметр.
3.3. Объем жидкости, протекающий за единицу времени через живое сечение называется
а) расход потока;
б) объемный поток;
в) скорость потока;
г) скорость расхода.
3.4. Отношение расхода жидкости к площади живого сечения называется
а) средний расход потока жидкости;
б) средняя скорость потока;
в) максимальная скорость потока;
г) минимальный расход потока.
3.5. Отношение живого сечения к смоченному периметру называется
а) гидравлическая скорость потока;
б) гидродинамический расход потока;
в) расход потока;
г) гидравлический радиус потока.
3.6. Если при движении жидкости в данной точке русла давление и скорость не изменяются, то такое движение называется
а) установившемся;
б) неустановившемся;
в) турбулентным установившимся;
г) ламинарным неустановившемся.
3.7. Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени называется
а) ламинарным;
б) стационарным;
в) неустановившимся;
г) турбулентным.
3.8. Расход потока обозначается латинской буквой
3.9. Средняя скорость потока обозначается буквой
3.10. Живое сечение обозначается буквой
3.11. При неустановившемся движении, кривая, в каждой точке которой вектора скорости в данный момент времени направлены по касательной называется
а) траектория тока;
б) трубка тока;
в) струйка тока;
г) линия тока.
3.12. Трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением называется
а) трубка тока;
б) трубка потока;
в) линия тока;
г) элементарная струйка.
3.13. Элементарная струйка — это
а) трубка потока, окруженная линиями тока;
б) часть потока, заключенная внутри трубки тока;
в) объем потока, движущийся вдоль линии тока;
г) неразрывный поток с произвольной траекторией.
3.14. Течение жидкости со свободной поверхностью называется
а) установившееся;
б) напорное;
в) безнапорное;
г) свободное.
3.15. Течение жидкости без свободной поверхности в трубопроводах с повышенным или пониженным давлением называется
а) безнапорное;
б) напорное;
в) неустановившееся;
г) несвободное (закрытое).
3.16. Уравнение неразрывности течений имеет вид
3.17. Уравнение Бернулли для идеальной жидкости имеет вид
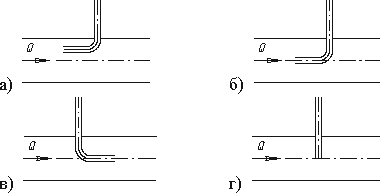
3.18. На каком рисунке трубка Пито установлена правильно
3.19. Уравнение Бернулли для реальной жидкости имеет вид
3.20. Член уравнения Бернулли, обозначаемый буквой z, называется
а) геометрической высотой;
б) пьезометрической высотой;
в) скоростной высотой;
г) потерянной высотой.
3.21. Член уравнения Бернулли, обозначаемый выражением 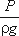
а) скоростной высотой;
б) геометрической высотой;
в) пьезометрической высотой;
г) потерянной высотой.
3.22. Член уравнения Бернулли, обозначаемый выражением 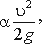
а) пьезометрической высотой;
б) скоростной высотой;
в) геометрической высотой;
г) такого члена не существует.
3.23. Уравнение Бернулли для двух различных сечений потока дает взаимосвязь между
а) давлением, расходом и скоростью;
б) скоростью, давлением и коэффициентом Кориолиса;
в) давлением, скоростью и геометрической высотой;
г) геометрической высотой, скоростью, расходом.
3.24. Коэффициент Кориолиса в уравнении Бернулли характеризует
а) режим течения жидкости;
б) степень гидравлического сопротивления трубопровода;
в) изменение скоростного напора;
г) степень уменьшения уровня полной энергии.
3.25. Показание уровня жидкости в трубке Пито отражает
а) разность между уровнем полной и пьезометрической энергией;
б) изменение пьезометрической энергии;
в) скоростную энергию;
г) уровень полной энергии.
3.26. Потерянная высота характеризует
а) степень изменения давления;
б) степень сопротивления трубопровода;
в) направление течения жидкости в трубопроводе;
г) степень изменения скорости жидкости.
3.27. Линейные потери вызваны
а) силой трения между слоями жидкости;
б) местными сопротивлениями;
в) длиной трубопровода;
г) вязкостью жидкости.
3.28. Местные потери энергии вызваны
а) наличием линейных сопротивлений;
б) наличием местных сопротивлений;
в) массой движущейся жидкости;
г) инерцией движущейся жидкоcти.
3.29. На участке трубопровода между двумя его сечениями, для которых записано уравнение Бернулли можно установить следующие гидроэлементы
а) фильтр, отвод, гидромотор, диффузор;
б) кран, конфузор, дроссель, насос;
в) фильтр, кран, диффузор, колено;
г) гидроцилиндр, дроссель, клапан, сопло.
3.30. Укажите правильную запись
3.31. Для измерения скорости потока используется
а) трубка Пито;
б) пьезометр;
в) вискозиметр;
г) трубка Вентури.
3.32. Для измерения расхода жидкости используется
а) трубка Пито;
б) расходомер Пито;
в) расходомер Вентури;
г) пьезометр.
3.33. Укажите, на каком рисунке изображен расходомер Вентури
3.34. Установившееся движение характеризуется уравнениями
3.35. Расход потока измеряется в следующих единицах
3.36. Для двух сечений трубопровода известны величины P1, υ1, z1 и z2. Можно ли определить давление P2 и скорость потока υ2?
а) можно;
б) можно, если известны диаметры d1 и d2;
в) можно, если известен диаметр трубопровода d1;
г) нельзя.
3.37. Неустановившееся движение жидкости характеризуется уравнением
3.38. Значение коэффициента Кориолиса для ламинарного режима движения жидкости равно
3.39. Значение коэффициента Кориолиса для турбулентного режима движения жидкости равно
3.40. По мере движения жидкости от одного сечения к другому потерянный напор
а) увеличивается;
б) уменьшается;
в) остается постоянным;
г) увеличивается при наличии местных сопротивлений.
3.41. Уровень жидкости в трубке Пито поднялся на высоту H = 15 см. Чему равна скорость жидкости в трубопроводе
Уравнение Бернулли
Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Уравнение Бернулли выглядит так:
Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.
Содержание статьи
Смысл уравнения Бернулли
По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.
Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.
В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.
Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.
Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.
Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную
Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.
В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид
Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.
Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.
Отсюда следует, что между напором и удельной энергией существует очень простая зависимость
где э – удельная энергия
Уравнение Бернулли для элементарной струйки реальной жидкости
Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.
При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.
Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет
Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается
Величина Э1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.
Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде
Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.
Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.
В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.
Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.
Слагаемое h1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— hлп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— hмп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости
Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет
Видео по теме
Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.
http://gidravl.narod.ru/test13.html
http://www.nektonnasos.ru/article/gidravlika/uravnenie-bernulli/

 . В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

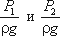 — удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
— удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;  — удельные кинетические энергии в тех же сечениях.
— удельные кинетические энергии в тех же сечениях.