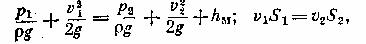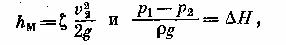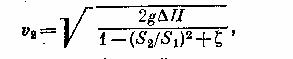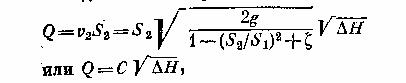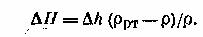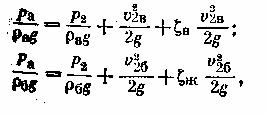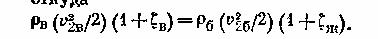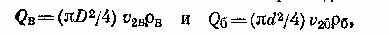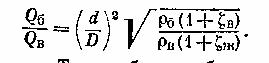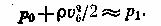Уравнение бернулли для потока реальной вязкой жидкости

Уравнение бернулли для потока реальной вязкой жидкости

6. Кинематика и динамика жидкости

(продолжение пятой лекции)

6.1 Уравнение Бернулли для потока реальной (вязкой) жидкости.

6.2 Мощность потока.

6.3 Коэффициент Кориолиса.

6.4 Гидравлические потери (общие сведения).

6.5 Местные потери.

6.6. Потери энергии на трение по длине

6.7.Примеры использования уравнения Бернулли в технике

6.1Уравнение Бернулли для потока реальной (вязкой) жидкости.

При переходе от струйки элементарной идеальной жидкости к потоку реальной (вяз­кой) жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность распределения скоростей по сечению, а также потери энергии. То и другое является следствием вязкости жидкости.

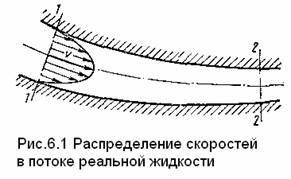
При движении вязкой жидкости вдоль твердой стенки в трубе, происхо­дит торможение потока из-за влияния вязкости, а также из-за действия сил молеку­лярного сцепления между жидкостью и стенкой. Поэтому наибольшего значения ско­рость достигает в центральной части потока, а по мере приближения к стенке она умень­шается почти до нуля. Получается распределение скоростей подобное тому которое показано на рис. 6.1.

Неравномерное распределение скоростей означает скольжение (сдвиг) одних слоев по другим, вследствие чего возникают касательные напряжения (напряжения трения). Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием . Это требует затрат энергии, поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивления и, следовательно, уменьшается вдоль потока.

Из-за неравномерного распределения скоростей при выводе уравнения Бернулли потока вязкой жидкости приходится вводить в рассмотрение среднюю по сечению скорость (см. лекцию №5), а также среднее значение удельной энергии жидкости в данном сечении. Измерения средней скорости потока практически выполнить проще и они могут быть сделаны с большей точностью.

Прежде чем приступить к рассмотрению уравнения Бернулли для потока вязкой жидкости сделаем следующее допущение: будем считать, что в пределах рассматриваемых поперечных сечений потока справедлив основной закон гидростатики, например, в первой форме, т. е. гидростатический напор в пределах рассматриваемых сечений есть величина одинаковая для всех точек данного сечения:

Предполагаем, что при движении жидкости отдельные струйки оказывают одна на другую в поперечном направлении такое же давление, как слои жидкости в неподвижном состоянии. Это может быть доказано в том случае, когда течение в данных поперечных сечениях является параллельно струйным. Поэтому именно такие (или близкие к ним) поперечные сечения и будем рассматривать.

6.2. Мощность потока

Введем понятие мощности потока. Мощностью потока в данном сечении будем называть полную энергию, которую проносит поток через это сечение в единицу времени. Так как в различных точках поперечного сечения потока частицы жидкости обладают различной энергией, сначала выразим элементарную мощность (мощность элементарной струйки) в виде произведения полной удельной энергии жидкости в данной точке на элементарный массовый расход dQ_m :

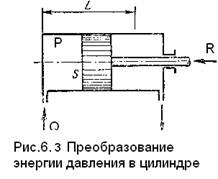
Рассмотрим мощность, как частное от деления работы на время. Выразим работу, как произведение давления на площадь, например гидроцилиндра, и путь, который проделывает поршень под действием этой силы.

Пусть площадь поршня равна s , его ход L , избыточное давление жидкости в левой полости цилиндра необходимое для преодоления силы F равно Р = F / S , избыточное давление по другую сторону поршня равно нулю. Преодолевая силу F при перемещении поршня из левого положения, давление совершает работу А = Р SL . Расход жидкости, которую необходимо подвести к цилиндру для совершения этой работы за время t , равен объему цилиндра, т. е. Q t = W = SL .Работа, выполняемая гидроцилиндром

N = F / dt = ( p * f * S )/ dt = p * Q – выражение для определения мощности гидравлического потока под действие силы Р.

Возьмем теперь третью форму уравнения Бернулли

умножим его на изменение массового расхода dQ_m .

Наличие в составе dQ_m плотности ρ преобразует третью форму у-я Бернулли(энергетическую) во вторую форму в виде суммы давлений, в результате получаем элементарную мощность потока.

Мощность всего потока найдем, как интеграл от предыдущего выражения по площади S :

N = ρ 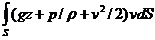(6.3)

Или, учитывая, сделанные допущения

N = ρ 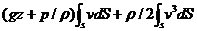(6.4)

Третья степень под интегралом получается при умножении квадрата скорости в сумме на скорость в первой степени.

6.3 Коэффициент Кориолиса

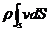
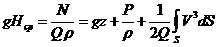
Найдем среднее по сечению значение полной удельной мощности жидкости делением этой величины на массовый расход, используя выражение для среднего массового расхода – ρ Q = , Q = v ср* S .), получим

(6.5)

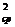
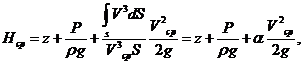
Поскольку среднюю скорость проще измерять, используем ее значение, умножив и разделив последний член на V , и получим, переходя к напорам, третья степень в знаменателе получается умножением на скорость в составе расхода

(6.6)

где α – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей и равный

(6.7)

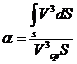
Если умножить числитель и знаменатель выражения (6.7) на ρ/2, можно убедиться, что коэффициент α представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечения, но при равномерном распределении скоростей, поскольку произведение dm = ρ* vdS –есть масса.

Для для течения вязкой жидкости скоростей (см. рис.6.1) коэффициент α не является величиной постоянной.

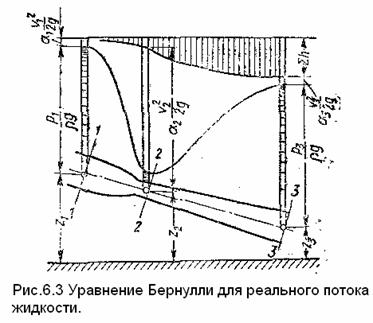
Возьмем два сечения реального потока, первое и второе, и обозначим средние значения полного напора жидкости в этих сечениях соответственно Н_ср1 и Н_ср2. Тогда

где Σ h _п — суммарная потеря полного напора на участке между рассматриваемыми сечениями.

Используя формулу для Нср, предыдущее уравнение можно переписать так:

(6.8)

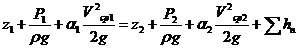
Это и есть уравнение Бернулли для потока вязкой жидкости. От аналогичного уравнения для элементарной струйки идеальной жидкости полученное уравнение отличается членом, представляющее собой потерю полного напора, и коэффициентами, учитывающим неравномерность распределения скоростей. Кроме того, скорости, входящие в это уравнение, являются средними по сечениям.

Уравнение Бернулли (6.8) и его формы применимы не только для жидкостей, но для газов при условии, что скорость их движения значительно меньше скорости звука.

Графически это уравнение можно представить диаграммой подобно тому, как это делали для идеальной жидкости, но с учетом потери напора. Последняя является некоторой высотой, которая неуклонно возрастает вдоль потока (рис. 1.27).

Для струйки идеальной жидкости уравнение Бернулли представляет собой закон сохранения механической энергии.

Для потока реальной жидкости уравнение Бернулли является уравнением баланса энергии с учетом потерь. Энергия, теряемая жидкостью на рассматриваемом участке течения, разумеется, не исчезает бесследно, превращаясь в другую форму — тепловую. Так как удельная теплоемкость жидкостей обычно велика по сравнению с потерями удельной энергии, а также ввиду того, что тепловая энергия непрерывно рассеивается, повышение температуры часто бывает практически малозаметным. Этот процесс преобразования механической энергии в тепловую является необратимым, т. е. таким, обратное течение которого (превращение тепловой энергии в механическую) невозможно

Уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единице его длины, называется гидравлическим уклоном.

Изменение удельной потенциальной энергии жидкости, отнесенное к единице длины, называется пьезометрическим уклоном. Очевидно, что в трубе постоянного диаметра с неизменным распределением скоростей указанные уклоны одинаковы.

6.4 Гидравлические потери (общие сведения).

Потери удельной энергии (напора), — гидравлические потери, зависят от формы и размеров трубопровода, скорости течения и вязкости жидкости.

При турбулентном движении гидравлические потери пропорциональны скорости во второй степени,

или в единицах давления

В это выражение входит безразмерный ζ коэффициент потерь, или коэффициент сопротивления.

Коэффициент потерь, таким образом, есть отношение величины потерянного напора к скоростному напору.

Гидравлические потери разделяют на местные потери и потери на трение по длине.

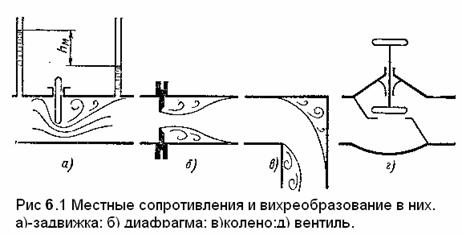
6.5.Местные потери энергии вызваны изменениями формы и размера трубопровода, вызывающими деформацию потока. Жидкости, протекая через местные сопротивления изменяет скорость и образует вихри. После отрыва потока от стенок вихри образуют области, в которых частицы жидкости движутся в основном по замкнутым траекториям.

Примерами местных сопротивлений устройства, изображенные на рис. 6.1. Здесь же показаны отрывы потока и вихреобразование.

Если диаметр трубы и, следовательно, скорость в ней изменяются по длине, то за расчетную скорость удобнее принимать большую из скоростей, т.е. ту, которая соответствует меньшему диаметру трубы.

Каждое местное сопротивление характеризует значение коэффициента сопротивления ζ, которое приближенно можно считать постоянным для данной формы местного сопротивления.

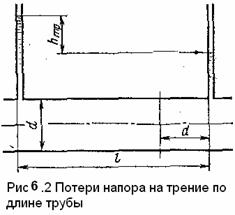
6.6. Потери энергии на трение по длине возникают в прямых трубах постоянного сечения, при равномерном течении, и возрастают пропорционально длине трубы (рис. 7. 2).

Эти потери обусловлены внутренним трением в жидкости. Потери напора на трение можно выразить по общей формуле (6.1) для гидравлических потерь, т. е.

Однако, удобнее коэффициент ζтр связать с относительной длиной трубы l / d .

Обозначим коэффициент потерь участка круглой трубы длиной l = d равной ее диаметру и обозначим его через λ. Для всей трубы длиной l и диаметром d не равным длине трубы, коэффициент потерь будет в l / d раз больше:

В результате формула (7.1) примет вид

(6.10)

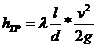
или в единицах давления

р_тр = λ* 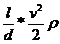. (6.11)

Формулу (6.10) называют формулой Вейсбаха — Дарси.

Коэффициент, входящий в выражение (6.2) называется коэффициент потерь на трение по длине λ , или коэффициентом Дарси.

(Физический смысл коэффициента λ. При равномерном движении в трубе длиной l и диаметром d , имеет место равновесие сил, действующих на объем: сил давления и силы трения. Это равновесие выражается равенством

где τ₀ — напряжение трения на стенке трубы.

Если учесть формулу (6.10), то

λ= ,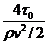

λ есть величина, пропорциональная отношению напряжения от силы трения на стенке трубы к динамическому давлению, определяемому по средней скорости.

Ввиду постоянства объемного расхода несжимаемой жидкости вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также остаются.

6.6. Применение уравнения Бернулли в технике

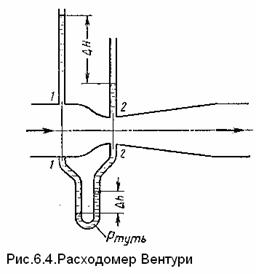
Расходомер Вентури — устройство, устанавливаемое в трубопроводах и выполняющее сужение потока — дросселирование (рис.6.4).

Расходомер состоит из двух участков — плавно сужающегося сопла и постепенно расширяющегося диффузора. Скорость потока в суженном месте возрастает, а давление падает. Возникает перепад давлений, который измеряется двумя пьезометрами или дифференциальным U -образным манометром. Эта разность связана с расходом.

В сечении 1-1 перед сужением скорость потока равна V ₁, давление Р₁, площадь сечения S ₁ , а в c ечении 2-2: V ₂, P ₂ , S ₂ , разность показаний пьезометров, присоединенных к сечениям ΔН.

Запишем для сечений 1-1 и 2-2 потока уравнение Бернулли и уравнение расхода, считая распределение скоростей равномерным.

где h м — потеря напора между сечениями 1-1 и 2-2.

найдем из этой системы уравнений одну из скоростей, например,

отсюда объемный расход

где С — величина постоянная для данного расходомера.

Зная величину С, можно найти расход в трубопроводе по формуле. Коэффициент С можно определить теоретически, но лучше найти его экспериментально при тарировании расходомера.

Вместо пьезометров для измерения перепада давлений в расходомере применяют дифференциальный манометр. Принимая что над ртутью в трубках находится та же жидкость, плотностью ρ, можно записать

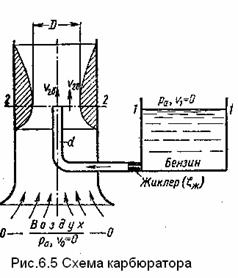
Карбюратор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешивания его с потоком воздуха (рис. 6.5). Поток воздуха засасываемого в двигатель, сужается в том месте, где установлен распылитель бензина (обрез трубки диаметром d ). Скорость воздуха этом сечении возрастает, а давление по закону Бернулли падает. Благодаря пониженному давлению бензин вытекает в поток воздуха.

Надем соотношение между массовыми расходами бензина Q б и воздуха Q в при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2-2) и жиклера ζж (сопротивлением бензотрубки пренебрегаем).

Записав уравнение Бернулли для потока воздуха (сечение 1-1 и 2-2), а затем для потока бензина (сечение 1-1 и 2-2), получим (при z ₁= z ₂‚ и α= 1):

Учитывая, что массовые расходы

Таким образом, обеспечивается постоянство соотношения расходов бензина и воздуха. Однако, следует иметь в виду приближенный характер данного решения.

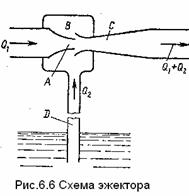
Струйный насос (эжектор) состоит из плавно сходящегося насадка А (рис.6.6), осуществляющего сжатие потока, и постепенно расширяющейся трубки С, установленной на некотором расстоянии от насадка в камере В.

Вследствие увеличения скорости потока в струе на выходе из насадка и по всей камере В значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно в камере В давление обычно меньше атмосферного, т. е. возникает разрежение (вакуум). Под действием разрежения жидкость из нижнего резервуара всасывается по трубе D в камеру В, где происходят слияние и дальнейшее перемешивание двух потоков.

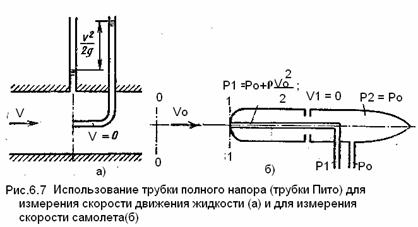
Трубка полного напора ( трубка Пито) служит для измерения скорости в трубе (рис. 1.34). Если установить в этом потоке трубку, повернутую под углом 90°, отверстием навстречу потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре на высоту равную скоростному напору.

Объясняется это тем, что скорость v частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно, увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито и пьезометре, легко определить скорость жидкости в данной точке. На этом же принципе основано измерение скорости полета самолета. На рис.1.35 показана схема самолетной скоростной трубки (насадка) для измерения малых по сравнению со скоростью звука скоростей полета.

Запишем уравнение Бернулли для струйки , которая набегает на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где v =0), получаем

Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, р₂ ≈ р₀ , следовательно, из предыдущего имеем

Уравнение Бернулли

Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Уравнение Бернулли выглядит так:

Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.

Содержание статьи

Смысл уравнения Бернулли

По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.

Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.

В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.

Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.

Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.

Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную

Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.

В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид

Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.

Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.

Отсюда следует, что между напором и удельной энергией существует очень простая зависимость

где э – удельная энергия

Уравнение Бернулли для элементарной струйки реальной жидкости

Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.

При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.

Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет

Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается

Величина Э_1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.

Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h_1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде

Уравнение Бернулли для потока реальной жидкости

Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.

Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.

В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.

Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.

Слагаемое h_1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— h_лп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— h_мп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости

Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет

Видео по теме

Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.

Гидродинамика. Уравнение Бернулли для потока реальной жидкости.

При трансформации закономерности Бернулли для идеальной жидкости к уравнению потока реальной жидкости требуется принимать во внимание неравномерность разделения скоростей по сечению потока и потери энергии жидкости на внутреннее трение, что объясняется вязкостью жидкости.

В реальной жидкости вязкость формирует сопротивление движению жидкости. Это вызывает появление дополнительных потерь напора (энергии потока).

Распределение скоростей элементарных струек в потоке обычно величины не определенные, для этого в уравнение Бернулли добавляют поправочный коэффициент α.

Коэффициент α принято называть коэффициентом кинетической энергии или коэффициентом Кориолиса. Он характеризует неравномерное распределение скоростей в живом сечении потока, и равняется соотношению кинетической энергии, рассчитанной по реальным скоростям сечения, к той же энергии, вычисленной по средней скорости в этом же сечении потока. Следовательно, указанный коэффициент применяется для преобразования результатов расчетов по средней скорости в соответствие с реальными скоростями.

При турбулентном типе (со значительным перемешиванием, выравнивающим скорости на всех участках потока) кинетическая энергия практически равна полученной через среднюю скорость. Среднее значение коэффициента α берем на промежутке 1,05 – 1,11.

При ламинарном типе (перемешивание отсутствует) неравномерность поля скоростей достаточно велика и кинетическая энергия в 2 раза больше, чем вычисленная по средней скорости, α = 2.

Формула Бернулли для двух сечений потока реальной жидкости записывают так:

.

Закономерность Бернулли для потока реальной жидкости с физической точки зрения демонстрирует уравнение энергетического баланса. Теряемая энергия трансформируется в тепловую.