Уравнение бернулли для простого трубопровода
При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора.
В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач.
Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.
Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.
Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.
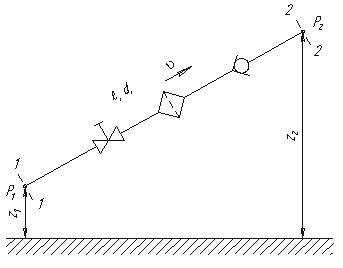
Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рис. 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна z1 и избыточное давление Р1, а в конечном сечении 2-2 — соответственно z2 и Р2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна ν.
Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α1 = α2, то скоростной напор можно не учитывать. При этом получим
Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Нпотр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Нрасп. Такой напор складывается из геометрической высоты Hпотр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту
а последнее слагаемое Σh — как степенную функцию расхода
где K — величина, называемая сопротивлением трубопровода;
Q — расход жидкости;
m — показатель степени, который имеет разные значения в зависимости от режима течения.
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
Численные значения эквивалентных длин lэкв для различных местных сопротивлений обычно находят опытным путем.
Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
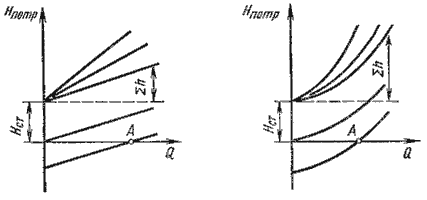
По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Нпотр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при турбулентном — параболой с показателем степени равном двум (рис.6.2, б).
Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.
Величина статического напора Нст положительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода. Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
Простые трубопроводы могут соединяться между собой, при этом их соединение может быть последовательным или параллельным.
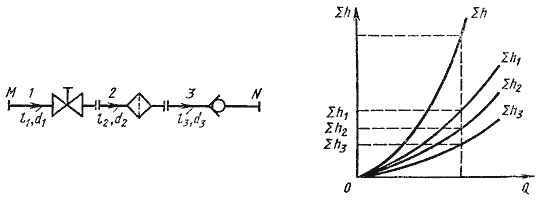
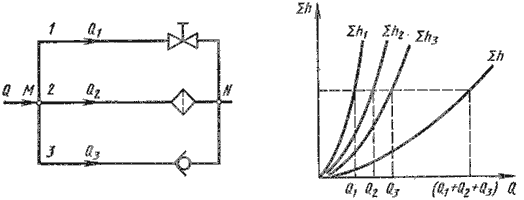
Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:
Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.
Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.
Обозначим полные напоры в точках М и N соответственно HM и HN , расход в основной магистрали (т.е. до разветвления и после слияния) — через Q, а в параллельных трубопроводах через Q1, Q2 и Q3; суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.
Очевидно, что расход жидкости в основной магистрали
Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :
Отсюда делаем вывод, что
т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом
где K и m — определяются в зависимости от режима течения.
Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.
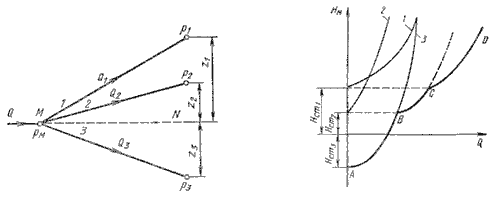
Разветвленное соединение. Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб.
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы 1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а). Геометрические высоты z1, z2 и z3 конечных сечений и давления P1, P2 и P3 в них будут также различны.
Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе:
Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот)
Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем
Аналогично для двух других трубопроводов можно записать
Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM.
Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) — сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM > Hст1.
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
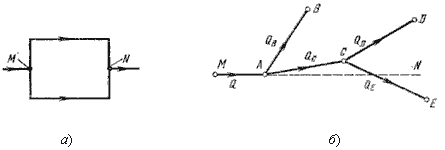
Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE .
Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M — N и избыточные давления в конечных точках PB и PD и PE.
Для этого случая возможны два вида задач:
Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М.
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви.
Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно:
уравнение равенства потребных напоров для ветвей CD и CE
уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD
выражение для потребного напора в точке М
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2).
Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.
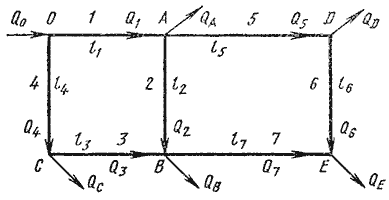
Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 6.7).
Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие — баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие — баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее.
Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках.
Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с насосной подачей жидкости.
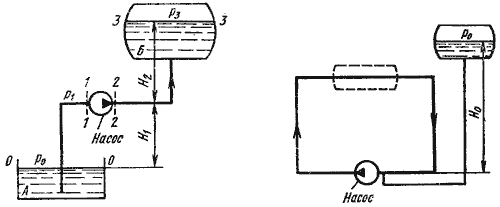
Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рис. 6.8, б).
Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P 0 в другой резервуар с давлением P3 (рис. 6.8, а). Высота расположения оси насоса H1 называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к насосу, всасывающим трубопроводом или линией всасывания. Высота расположения конечного сечения трубопровода H2 называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией нагнетания.
Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений 0-0 и 1-1 (принимая α = 1):
Это уравнение является основным для расчета всасывающих трубопроводов.
Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений 2-2 и 3-3:
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса энергию жидкости можно будет аналогично выразить из уравнения:
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается жидкости насосом и поэтому обозначается обычно Hнас.
Для нахождения напора Hнас вычислим уравнение :
где Δz — полная геометрическая высота подъема жидкости, Δz = H 1 + H2;
КQ m — сумма гидравлических потерь,
P3 и Р0 — давление в верхней и нижней емкости соответственно.
Если к действительной разности уровней Δz добавить разность пьезометрических высот ( P3 — Р0 ) ( ρg ), то можно рассматривать увеличенную разность уровней
и формулу можно переписать так:
Из этой формулы делаем вывод, что
Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.
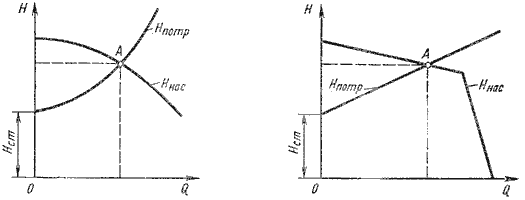
На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр = f1(Q) и характеристики насоса Hнас = f2(Q) и в нахождении их точки пересечения (рис. 6.9).
Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а — для турбулентного режима; б — для ламинарного режима. Точка пересечения кривой потребного напора с характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения вала насоса.
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.
Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено мгновенное закрытие крана (рис. 6.10, а).
При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔPуд, которое называется ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).
Далее под действием перепада давления ΔPуд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P0 (рис. 6.10, в).
Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь в противоположную теперь сторону.
С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P0 — ΔPуд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.
Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ0.
Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.
Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.
Уравнение бернулли для простого трубопровода
Уравнение Бернулли для реальной и идеальной жидкости
Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.
График Бернулли и уравнение Бернулли для идеальной жидкости:
График Бернулли и уравнение Бернулли для реальной жидкости:
Смысл уравнения Бернулли
Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.
Назначение уравнения Бернули
Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.
Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации
Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет — написано тут: Конструктор водяного отопления
Задача. Пример решения уравнения Бернулли
По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.
Как понять уравнение Бернулли?
Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве
Точка 1 – это место где известно давление
Точка 2 – это место где нужно узнать давление
Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)
То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.
Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)
Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.
Сборка формулы уравнения Бернулли
Как избавится от минуса?
Как избавится от множителя (-1)?
Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.
Что такое идеальная жидкость?
Идеальная жидкость — это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.
Реальная жидкость — это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.
Формула Бернулли для реальной жидкости
Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.
Потому что реальная жидкость движется не равномерно
У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.
Формула коэффициента Кориолиса
Что такое коэффициент Кориолиса?
Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.
Чему равен коэффициент Кориолиса?
Нд.п. – Это динамические потери. Это потери вызванные движением воды.
Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:
Посмотрите видеоурок по составлению уравнения Бернулли:
Как сделать гидравлический расчет погружного насоса?
Гидравлика курсач. Гидравлический расчет трубопровода
| Название | Гидравлический расчет трубопровода |
| Дата | 22.04.2021 |
| Размер | 453.4 Kb. |
| Формат файла |  |
| Имя файла | Гидравлика курсач.docx |
| Тип | Реферат #197715 |
 С этим файлом связано 1 файл(ов). Среди них: Задача Осложнённые условия.docx. С этим файлом связано 1 файл(ов). Среди них: Задача Осложнённые условия.docx.  Показать все связанные файлы Подборка по базе: ЭТС Курсач Леша.docx, Примеры расчётов.doc, Курсовая расчеты.docx, 1 Кинематический и силовой расчет привода (2).pdf, Акустические расчеты Практика Латыповой О.А.гр.ПТМз-514_compress, внб курсач 2_merged.pdf, тест Алгоритм расчета по аккредитиву_бо.docx, курсовая работа гидравлика Чернышов.docx, математика 1 типовой расчет.pdf, ГМз-19-1 Алексеев А.С Практическая работа № 8 Проектный и провер Показать все связанные файлы Подборка по базе: ЭТС Курсач Леша.docx, Примеры расчётов.doc, Курсовая расчеты.docx, 1 Кинематический и силовой расчет привода (2).pdf, Акустические расчеты Практика Латыповой О.А.гр.ПТМз-514_compress, внб курсач 2_merged.pdf, тест Алгоритм расчета по аккредитиву_бо.docx, курсовая работа гидравлика Чернышов.docx, математика 1 типовой расчет.pdf, ГМз-19-1 Алексеев А.С Практическая работа № 8 Проектный и проверфилиал федерального государственного бюджетного образовательного учреждения высшего образования «Российский государственный университет нефти и газа (национальный исследовательский университет) имени И.М. Губкина» в г. Оренбурге 21.03.01 «Нефтегазовое дело» « Эксплуатация и обслуживание объектов добычи нефти» по дисциплине «Гидравлика и нефтегазовая гидромеханика» «Гидравлический расчет трубопровода» Руководитель работы доктор технических наук, доцент «___» ______ 2019 г. Выполнил студент группы ОРНз-16-01 .Эж.южюжю…. _____________Юртаев Н.Г.Ээ.. «___» ______ 2019 г. 1. Уравнение Бернулли для потока вязкой жидкости……………. 5 2. Виды потерь напора……………………………………………. 8 3. Расчет трубопроводов…………………………………………….10 3.1 Расчет простых трубопроводов……………………………….. .10 3.2 Расчет сложных трубопроводов……………………………….. 12 Список используемой литературы…………………………………16 В данной курсовой работе изучено уравнение Бернулли и произведен анализ методов расчета для простых и сложных трубопроводов. Представленная курсовая работа состоит из введения, трех глав, заключения и списка используемой литературы Работа состоит из 16 страниц, содержит 10 литературных источника, 5 рисунков. Актуальность темы исследования: Гидравлика — механика жидкости (гидромеханика) является общепрофессиональной дисциплиной, при изучении которой студенты знакомятся с физическими свойствами жидкости, основными законами кинематики, гидростатики и гидродинамики, теоретическими основами ламинарного и турбулентного режимов движения жидкости и др. Гидравлика содержит большое число опытных коэффициентов, эмпирических и полуэмпирических формул, методика применения которых, а также их физический смысл хорошо осваиваются в процессе решения различных задач. Технологическими трубопроводами называют такие трубопроводы промышленных предприятий, по которым транспортируют смеси, полупродукты и готовые продукты, отработанные реагенты, воду, топливо и др. материалы, обеспечивающие ведение технологического процесса. С помощью технологических трубопроводов на предприятиях перемещают продукты как между отдельными аппаратами в пределах одного цеха или технологической установки, так и между технологическими установками и отдельными цехами, подают исходное сырье из хранилищ или транспортируют готовую продукцию к месту ее хранения. При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности (расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода на заданных расходе и потерях напора. Цель работы: исследование видов гидравлических расчетов трубопроводов Задачи исследования:
1. Уравнение Бернулли для потока вязкой жидкости Уравнение Бернулли для потока вязкой жидкости представляет собой одно из основных соотношений, используемых для гидравлического расчета трубопроводов. Для его вывода введем следующие предположения: а) движение установившееся; б) жидкость несжимаемая, сonst = ρ; в) из массовых сил действует только сила тяжести. В этих предположениях закон изменения кинетической энергии имеет вид: Распределение давления имеет место при ламинарном режиме течения в призматических трубах. Однако приближенно этот закон может быть распространен также на осредненное прямолинейное турбулентное течение и на плавно изменяющиеся течения, то есть на течения, при которых площадь и форма поперечного сечения мало меняются по длине трубы. Произведение ускорения силы тяжести на массовый расход m Q представляет собой весовое количество жидкости, протекающей через поперечное сечение в единицу времени, и называется весовым расходом. Поток кинетической энергии реального течения равен: где α — поправочный коэффициент, возникающий за счет неравномерности распределения скоростей по поперечному сечению – так называемый коэффициент Кориолиса. Члены уравнения Бернулли так же, как и члены интеграла Бернулли, имеют размерность длины и называются: z — геометрический напор, или геометрическая высота; H= Уравнение Бернулли допускает простую графическую интерпретацию. Будем откладывать вдоль оси абсцисс расстояние, отсчитываемое вдоль оси потока, а вдоль оси ординат — напоры. Линия А на рис.1 характеризует положение оси потока относительно плоскости отсчета z=0 . Расстояние от линии В до оси абсцисс равно z + Уравнение Бернулли является фундаментальным уравнением гидродинамики. Оно устанавливает зависимость между давлением, средней скоростью и геометрической высотой в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач. Уравнение Бернулли для потока реальной жидкости (при установившемся движении) для двух сечений трубопровода, находящихся на расстоянии где При движении реальной вязкой жидкости возникают гидравлические сопротивления (вызванные силами трения между слоями жидкости при ее движении и местными сопротивлениями), на преодоление которых затрачивается энергия. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии при движении жидкости от сечения 1-1 до сечения 2-2. В уравнении Бернулли (5) появились два коэффициента α1 и α2, которые называются коэффициентами Кориолиса (кинетической энергии) и зависят от режима течения жидкости (α = 2 для ламинарного режима, α = 1 для турбулентного режима). 2. Виды потерь напора При движении жидкости по трубопроводу различают два вида потерь: потери по длине и потери в местных сопротивлениях. Местными сопротивлениями называются различные устройства малой длины (по сравнению с длиной трубы), в которых происходит резкое изменение скорости по величине или направлению, или по величине и направлению. К местным сопротивлениям относятся различные запорные устройства, повороты, клапаны и т.д. Местные сопротивления — это участки локальных изменений геометрии потока. Таким образом, местные потери обусловлены изменением формы потока (вход в трубу), изменением диаметра трубы (внезапное расширение трубопровода, внезапное сужение трубопровода, постепенное расширение трубопровода, краны, фильтры, распределители, угольники, клапана и т.д.). Потери напора в местных сопротивлениях где ζ – коэффициент местного сопротивления (величина безразмерная); – максимальное значение средней скорости потока. Величина коэффициента местного сопротивления ζ зависит не только от типа местного сопротивления (внезапное расширение, внезапное сужение, поворот трубы, вход в трубу, задвижка и т.д.), но и от режима движения жидкости и её вязкости. Величина коэффициента местного сопротивления ζ зависит не только от типа местного сопротивления (внезапное расширение, внезапное сужение, поворот трубы, вход в трубу, задвижка и т.д.), но и от режима движения жидкости и её вязкости. Приведённые во многих справочных пособиях значения коэффициентов местных сопротивлений имеют экспериментальную основу и определены для квадратичной зоны сопротивления. Для некоторых типов местных сопротивлений рекомендуются следующие формулы: при внезапном расширении трубопровода ( 3.1 Расчет простых трубопроводов Простым называется трубопровод постоянного диаметра без разветвлений и местных сопротивлений. Все остальные трубопроводы называются сложными. Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа. Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна z1 и избыточное давление Р1, а в конечном сечении 2-2 — соответственно z2 и Р2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна ν. Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α1 = α2, то скоростной напор можно не учитывать. При этом получим : Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Нпотр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Нрасп. Такой напор складывается из геометрической высоты Hпотр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе. Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту: а последнее слагаемое Σh — как степенную функцию расхода Σ h = KQm , то где K — величина, называемая сопротивлением трубопровода; Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно: Численные значения эквивалентных длин lэкв для различных местных сопротивлений обычно находят опытным путем. Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем 3.2 Расчет сложных трубопроводов Трубопроводы, в которых имеются местные сопротивления, либо состоящие из труб разного диаметра, либо имеющие разветвления, называются сложными. Рассмотрим схемы расчета наиболее типичных сложных трубопроводов. Начнем с рассмотрения последовательного соединения. Это сложный трубопровод, состоящий из последовательного соединения труб, между которыми находятся местные сопротивления. При этом трубы могут быть как одного, так и разных диаметров (рис. 3). Трубопровод рассчитывают как систему из простых трубопроводов с местными сопротивлениями. Расход жидкости на всех участках одинаков. Потери на участке рассчитываются так же, как для простого трубопровода, а суммарные потери на участке между сечениями 1–1 и 2–2. При этом предполагается, что все геометрические элементы трубопровода и свойства жидкости известны. Для последовательного соединения можно построить расходную характеристику, используя схему вычислений для простого трубопровода. Расходная характеристика позволяет, как и в случае простого трубопровода, найти расход жидкости, если заданы давления в начале и конце трубопровода. При решении ряда технических задач (увеличение пропускной способности, повышение надежности перехода через реку и т.д.) используются параллельные соединения. Параллельное соединение представляет собой трубопровод, состоящий из нескольких труб, имеющих общее начало и конец (рис. 4) Рассмотрим параллельное соединение, состоящее из двух труб, и для каждой из них запишем уравнение Бернулли между сечениями 1–2 и 1а–2а, соответственно. Тогда Так как сечения 1 и 1а, а также сечения 2 и 2а расположены в непосредственной близости друг от друга, то можно считать, что Перейдем к определению потерь напора на участке А–В (рис. 4). Применять для этого уравнение Бернулли нельзя, так как на рассматриваемом участке имеются разветвления. Однако, можно утверждать, что потери энергии на участке А-B равны. Так как Расход жидкости до разветвления Q равен сумме расходов в ветвях. После подстановки этого соотношения в равенство получим: Совершенно аналогичные выводы получаются для разветвлений с любым числом параллельных ветвей. Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости. Сложный кольцевой трубопровод . Представляет собой систему смежных замкнутых контуров, с отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках. Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа). При этом основываются на двух обязательных условиях. Первое условие — баланс расходов, т.е. равенство притока и оттока жидкости для каждой узловой точки. Второе условие — баланс напоров, т.е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее. Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и длины семи участков. Требуется определить диаметры трубопроводов на всех участках. На основе проведенного изучения и анализа в работе были сделаны следующие выводы:
— расход жидкости через трубопровод; — геометрическое положение центров тяжестей поперечных сечений трубопровода; — конструктивные параметры трубопровода: диаметры и длина трубопровода; — физические свойства рабочей жидкости. 4. При расчете трубопровода принимается ряд допущений, основными из которых являются следующие: рабочая жидкость считается несжимаемой; температура жидкости, основные физические свойства жидкости (плотность, вязкость, модуль объемной упругости и др.) принимаются постоянными; рассматривается установившееся движение жидкости; коэффициенты гидравлических сопротивлений постоянны; разрыва потока жидкости не происходит. 5. Уравнение Бернулли является фундаментальным уравнением гидродинамики, устанавливающее зависимость между давлением, средней скоростью и геометрической высотой в различных сечениях потока. С помощью этого уравнения решается большой круг задач. 1. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика: учебное пособие для вузов — М.-Ижевск: Институт компьютерных исследований, 2005. — 544 с. 2. Гидравлика и аэродинамика: учебник для вузов / А.Д. Альштуль — М.: Стройиздат, 1987; 3. Галдин Н.С. Основы гидравлики и гидропривода: учебное пособие /Н.С.Галдин. – Омск: Изд-во СибАДИ, 2010. – 145 с. 4. Галдин Н.С, Семенова И.А. Гидравлический расчет простого трубопровода: Методические указания для курсового проектирования по дисциплине «Основы гидромеханики» /Сост. Н.С.Галдин . И.А. Семенова – Омск: Изд-во СибАДИ, 2012. – 20 с 5. Гиргидов А.Д. Механика жидкости и газа : Учебник для вузов /А.Д.Гиргидов; СПб. – СПбГПУ, 2002.- 545с. 6. Идельчик И.Е. Справочник по гидравлическим сопротивлениям /И.Е.Идельчик. – М.: Машиностроение, 1975. – 560 с. /А.В.Лепешкин, А.А.Михайлин, А.А.Шейпак. – М.: МГИУ, 2003 . – 352 с. 8. Чугаев Р.Р. Гидравлика (техническая механика жидкости) : учебник /Р.Р.Чугаев. – М.: Бастет, 2008. — 672 с. 9. Троян Т.П. Гидравлика. Задачи и примеры расчётов по гидростатике и гидродинамике: Учебное пособие. / Т.П.Троян. – Омск: Изд-во СибАДИ, 2006. -92 с. 10 . Угинчус А.А. Гидравлика и гидравлические машины : учебник источники: http://infosantehnik.ru/str/91.html http://topuch.ru/gidravlicheskij-raschet-truboprovoda/index.html |
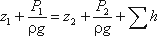
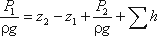
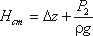
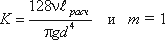
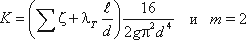
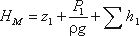
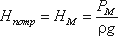
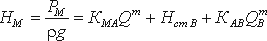
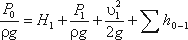
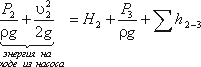
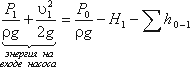
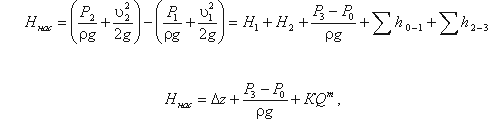
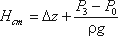




















 =
=  dV+
dV+  dS+
dS+ 

 — пьезометрический напор, или пьезометрическая высота;
— пьезометрический напор, или пьезометрическая высота; — потери напора на участке 1–2;
— потери напора на участке 1–2; — скоростной напор, или скоростная высота;
— скоростной напор, или скоростная высота; — полный напор.
— полный напор.
 друг от друга, имеет вид:
друг от друга, имеет вид: +
+  +
+  =
=  +
+  +
+  +
+  ,
, -геометрические высоты сечений 1-1 и 2-2 соответственно;
-геометрические высоты сечений 1-1 и 2-2 соответственно;  — коэффициент кинетической энергии (Кориолиса) соответственно в сечениях 1–1 и 2–2, принимаем
— коэффициент кинетической энергии (Кориолиса) соответственно в сечениях 1–1 и 2–2, принимаем  ;
;  — средние скорости жидкости в сечениях 1-1 и 2-2;
— средние скорости жидкости в сечениях 1-1 и 2-2;  определяются по формуле Вейсбаха:
определяются по формуле Вейсбаха: ζ
ζ >
>  ) ζ =
) ζ =  ; (9) при внезапном сужении трубопровода (
; (9) при внезапном сужении трубопровода ( 
 или
или 



 +
+  +
+  =
=  +
+  +
+  +
+  ,
, +
+  +
+  =
=  +
+  +
+  , где верхние индексы означают номер трубы.
, где верхние индексы означают номер трубы. =
=  ,
,  =
= 
 =
=  +
+  +
+  +
+ 
 — удельные по весу потери, то
— удельные по весу потери, то =
= 
 =
=  +
+ 
