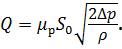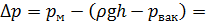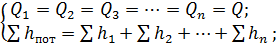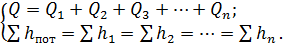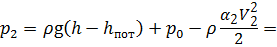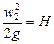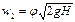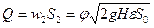Трубка Пито. Принцип работы | Теория
Измерение скорости потока и расхода жидкости
Рассмотрим применение уравнения Бернулли для измерения скорости потока с помощью таких несложных приборов, как трубка Пито — Прандтля, расходомер Вентури.
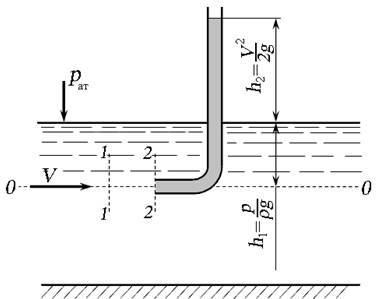
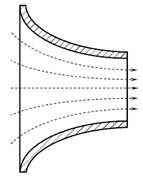
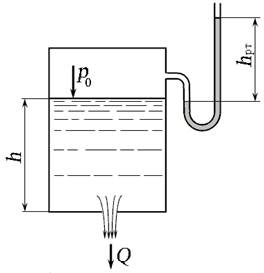
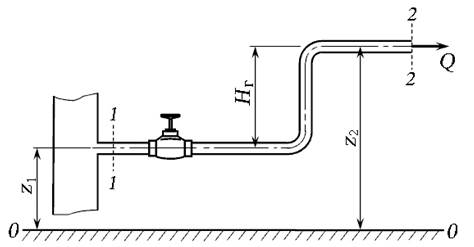
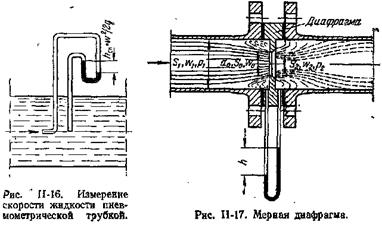
Для определения скорости безнапорного потока (например, в канале) используют трубку Пито, которая представляет собой изогнутую под прямым углом трубку небольшого диаметра, устанавливаемую в потоке открытым нижним концом навстречу движению жидкости (рис. 3.9).
Рис. 3.9. Трубка Пито
Плоскость сравнения — расположим по оси горизонтальной части трубки. Выберем сечение 1 — 1 на некотором расстоянии от трубки, и сечение 2 — 2 на входе в трубку. Геометрические высоты центра тяжести сечений z 1 и z 2 равны нулю. В центре тяжести сечения 1 — 1 жидкость обладает кинетической энергией 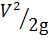
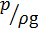
При попадании частиц жидкости в трубку их скорость становится равной нулю, кинетическая энергия переходит в потенциальную, и жидкость в трубке поднимется над свободной поверхностью на высоту h 2, равной скоростному напору. В центре тяжести сечения 2 — 2 жидкость обладает потенциальной энергией высоты столба жидкости h 1, и потенциальной энергией, равной кинетической. Составим уравнение Бернулли без учёта потерь напора h пот:
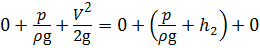

Скорость движения жидкости 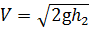
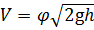
где h — высота столба жидкости в трубке над уровнем свободной поверхности.
Давление в трубке на уровне свободной поверхности создано за счёт кинетической энергии потока жидкости:

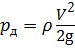
где р д — гидродинамическое давление.
Давление жидкости, создаваемое скоростным напором, называется гидродинамическим давлением.
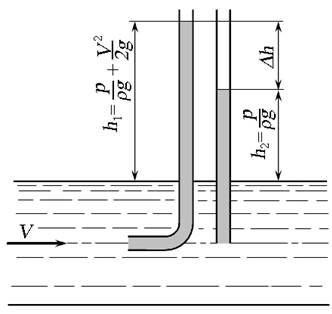
Для определения скорости напорного потока рассмотрим применение трубки Пито — Прандтля, которая представляет собой совмещённые в один прибор трубку Пито и обычный пъезометр (рис. 3.10). Высота столба жидкости в трубке Пито образована за счёт гидростатического и гидродинамического давления, в пъезометре — только гидростатического.
Рис. 3.10. Трубка Пито — Прандтля
Разность уровней жидкости в трубках ∆h даёт значение скоростного напора 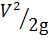
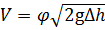
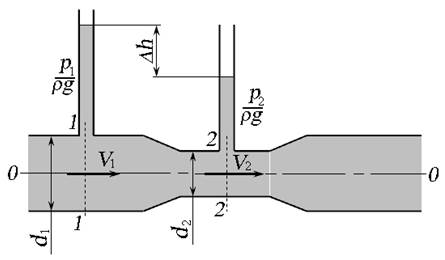
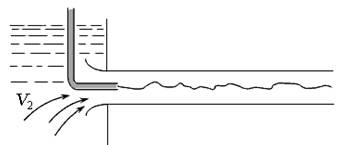
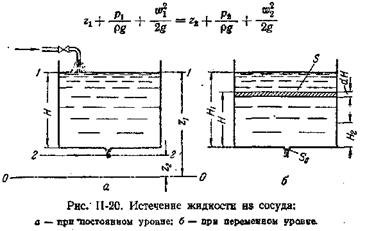
Расходомер Вентури представляет собой плавно сужающуюся и расширяющуюся цилиндрическую вставку устанавливаемой в трубе (рис. 3.11). В расширенной и в суженной частях расходомера установлены пъезометры.
Рис. 3.11. Расходомер Вентури
Составим уравнение Бернулли относительно плоскости сравнения, совпадающей с осью расходомера. Сечения выберем в местах подключений пъезометров. Так как центр тяжести сечений лежит в плоскости сравнения, геометрические высоты z 1 и z 2 равны нулю.
Для идеальной жидкости без учёта потерь напора h пот уравнение Бернулли примет вид:
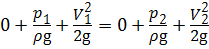
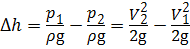
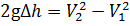
Из уравнения неразрывности потока:
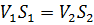
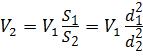
Подставим значение скорости V 2 из уравнения (3.11) в уравнение (3.12):
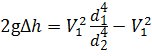
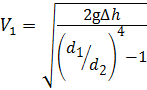
Так как скорость V 1 — это скорость потока идеальной жидкости, то расход, определённый с этой скоростью, будет теоретическим:

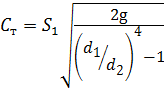
где С т — теоретическая постоянная расходомера.
Действительный расход жидкости:
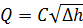

где С — действительная постоянная расходомера;
k — коэффициент, который учитывает потери напора при движении жидкости в расходомере, определяется опытным путём.
Режимы течения жидкости
Существуют два режима течения жидкости — ламинарный и турбулентный.
Движение жидкости, при котором отсутствуют изменения (пульсации) векторов местных скоростей, называют ламинарным (от латинского слова «lamina» – слой). Жидкость при этом рассматривается как совокупность отдельных слоёв, движущихся с разными скоростями, не перемешиваясь друг с другом. Движение жидкости, при котором происходят изменения (пульсации) векторов местных скоростей, приводящие к перемешиванию жидкости, называют турбулентным (от латинского слова «turbulentus» – беспорядочный, хаотичный).
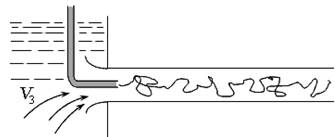
Исследование течений жидкости в круглой трубе провёл О. Рейнольдс в 1883 году на установке, изображённой на рис. 3.12. В начале стеклянной трубы он поместил тонкую трубку с подкрашенной жидкостью, плотность которой была равнозначна плотности основного потока жидкости. При небольшой скорости течения струйка подкрашенной жидкости двигается практически прямолинейно и горизонтально, что доказывает слоистое (ламинарное) течение жидкости (рис. 3.12, а ).
Рис. 3.12. Режимы течения жидкости:
а ) — ламинарный; б ) — переходный; в ) — турбулентный
При увеличении скорости течения основного потока струйка приобретает волнистый характер, у неё появляются разрывы, что характерно для неустойчивого, переходного режима (рис. 3.12, б ). При дальнейшем увеличении скорости основного потока подкрашенная струйка полностью смешивается с жидкостью, что доказывает беспорядочное (турбулентное) течение (рис. 3.12, в ).
Для характеристики режима течения жидкости принят безразмерный критерий — число Рейнольдса Re . Для круглых труб диаметром d :

где ν — коэффициент кинематической вязкости.
На основании опытов для круглых труб при напорном течении критическое число Рейнольдса, при котором турбулентный режим переходит в ламинарный, равно Re = 2300. Скорость потока жидкости, соответствующая смене режима течения, называется критической скоростью .
Для практических расчётов принято считать:
— при Re Re > 2300 существует турбулентный режим течения.
Вместо диаметра в число Рейнольдса может входить другой линейный параметр, характерный для данного живого сечения. Для труб некруглой формы или для безнапорного потока, образующего свободную поверхность, характерным линейным размером является гидравлический радиус R , определяемый соотношением (3.1):
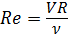
Критическое число Рейнольдса, записанное по гидравлическому радиусу, равно Re ≈ 580.
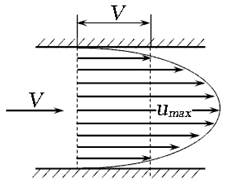
Рис. 3.13. Эпюра скоростей при ламинарном режиме
Для ламинарного режима течения эпюра местных скоростей по живому сечению имеет вид параболы (рис. 3.13), средняя скорость V потока в два раза меньше максимальной ( 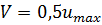
Турбулентный режим движения характеризуется непрерывным перемешиванием частиц жидкости. Скорости частиц в любой точке потока непрерывно и постоянно изменяются во времени, то есть пульсируют по величине и направлению относительно среднего значения . Для турбулентного режима характерны такие понятия, как мгновенная и осреднённая скорость.
Мгновенная скорость u — это скорость частицы жидкости в данной точке в данный момент времени. Так как мгновенная скорость хаотична во времени, её можно разложить в трёхмерной системе координат на продольную ux , поперечные uy и uz ( 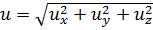
Осреднённая скорость 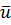
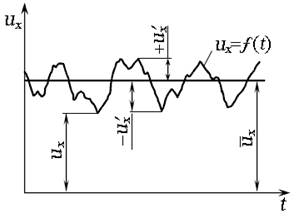
Рис. 3.14. График пульсации мгновенной местной скорости:

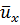
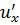
Рассмотрим график изменения продольной мгновенной скорости ux во времени (рис. 3.14). Величина осреднённой (во времени) скорости 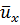
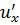
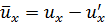
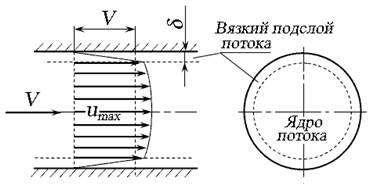
В живом сечении при турбулентном режиме различают ядро потока , в котором местные осреднённые скорости изменяются незначительно, и вязкий подслой потока толщиной δ (дельта), (рис. 3.15). Средняя скорость потока равна 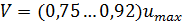
Рис. 3.15. Схема течения жидкости при турбулентном течении
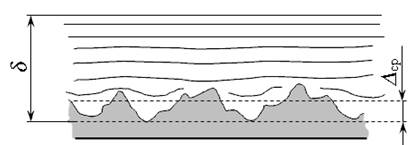
Вязкий подслой потока иначе называют ламинарным подслоем. Соотношение высоты шероховатости внутренних стенок трубопровода и ламинарного подслоя потока характеризует ограничивающие жидкость поверхности как гидравлически гладкие, или гидравлически шероховатые. За высоту шероховатости стенок принимают среднюю высоту ∆ср.
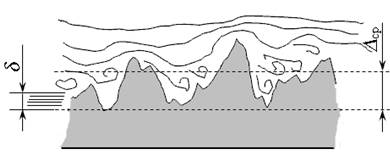
Рис. 3.16. Шероховатость поверхности при турбулентном движении:
а ) — гидравлически гладкая; б ) — гидравлически шероховатая
Если толщина ламинарного подслоя значительно больше, чем средняя высота шероховатости ( δ > ∆ ср), то такую поверхность называют гидравлически гладкой (рис. 3.16, а ). В этом случае шероховатость не влияет на сопротивление движению жидкости.
Если толщина ламинарного подслоя меньше выступов средней шероховатости ( δ ∆ ср), то такую поверхность называют гидравлически шероховатой (рис. 3.16, б ). В этом случае при обтекании выступов шероховатости усиливается турбулизация потока, что приводит к увеличению сопротивления движения жидкости и потерь напора.
Щелевые зазоры являются элементами гидравлических устройств, в которых скорость жидкости не достигает значений, вызывающих её турбулентность. В щелевых зазорах течение жидкости является ламинарным . Как правило, плотность соединения подвижных пар гидроагрегатов обеспечивается выполнением малого (микронного) зазора. Плотность щелевых уплотнений основано на физических свойствах реальных жидкостей оказывать сопротивление деформациям сдвига.
Различают плоские и кольцевые зазоры.
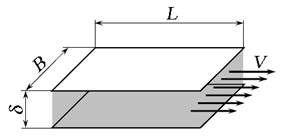
Рис. 3.17. Схема течения жидкости через плоский зазор
Рассмотрим случай плоского зазора , когда течение жидкости через него возникает под действием перепада давления ∆р (рис. 3.17). Расход жидкости в зазоре между пластинами будет равен:

где ∆р — перепад давлениий, под действием которого происходит течение жидкости в зазоре, 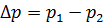
δ, В и L — высота, ширина и длина зазора;
μ — коэффициент динамической вязкости.
Скорость течения жидкости в зазоре 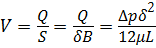
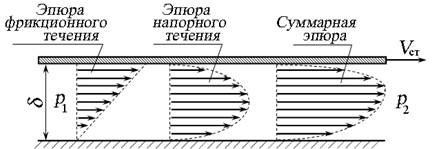
Если одна из стенок, образующих зазор, перемещается параллельно другой с некоторой скоростью V ст, течение жидкости рассматривают как сумму двух течений:
— так называемого фрикционного течения, образованного перемещением верхней стенки;
— напорного течения, образованного перепадом давлений ∆р .
Рис. 3.18. Распределение скоростей в плоском зазоре
с движущейся стенкой и перепадом давления
Распределение скоростей при движении одной из стенок будет зависеть от направления движения стенки (рис. 3.18). В этом случае расход будет учитывать скорость перемещения и направление движения стенки:
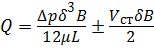
Первое слагаемое уравнения (3.18) определяет напорное течение под действием перепада давления ∆р , второе — фрикционное течение, учитываемое со знаком « » при совпадении направлений движения жидкости и стенки, со знаком «–» при разнонаправленном движении.
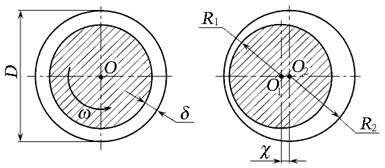
Рис. 3.19. Схема соосного (а) и эксцентричного (б)
расположения цилиндрических поверхностей
Кольцевые зазоры образованы двумя соосно расположенными цилиндрическими поверхностями, например, цилиндр — поршень, золотник — внутренняя поверхность корпуса гидрораспределителя. Расход через кольцевой зазор определяют по формуле (3.18), где B = πD :
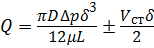
Для определения расхода жидкости в кольцевом зазоре, образованном эксцентричными цилиндрическими поверхностями, пользуются зависимостью:
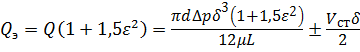
где Q — расход в зазоре при соосном расположении цилиндрических поверхностей;
d — диаметр внутренней цилиндрической поверхности;
ε — относительный эксцентриситет, 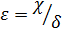
χ — величина эксцентриситета;
δ — номинальный зазор.
Ламинарное движение вязкой жидкости в малом зазоре толщиной δ является основой гидродинамической теории смазки между трущимися поверхностями, в частности, создание смазочного слоя в подшипниках скольжения.
Примеры решения задач
В данном разделе представлены примеры решения простейших задач, связанных с определением параметров движущейся идеальной жидкости. Основными уравнениями, позволяющими определить скорость, расход и давление движущейся идеальной жидкости, являются:
— уравнение постоянства расхода (3.3) 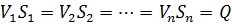
— уравнение Бернулли для идеальной жидкости без учёта потерь напора h пот и коэффициента Кориолиса α (3.8)
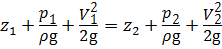
Правила применения уравнения Бернулли рассмотрены в п. 3.5. Уравнение Бернулли рекомендуется вначале записать в общем виде, затем переписать его с учётом действующих в выбранных сечениях геометрического, гидростатического (или пъезометрического) и скоростного напора относительно плоскости сравнения. Члены уравнения, равные нулю, следует исключить. Также необходимо чётко представлять разницу между избыточным, вакуумметрическим и абсолютным давлением.
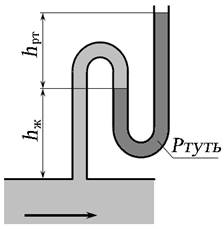
Рис. 3.20. Ртутный пъезометр
Если сечение выбирается в месте подключения ртутного пъезометра (рис. 3.20), то пъезометрическая высота будет равна:
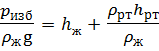
где ρ ж и ρ рт — плотность жидкости в трубопроводе и ртути в пъезометре;
h ж и h рт — высота столба жидкости и ртути в пъезометре.
Задачи, связанные с течением жидкости в узких щелях, решают по формулам, представленным в п. 3.8.
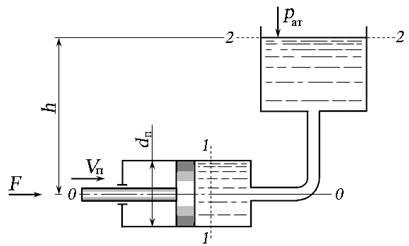
Задача 3.9.1. Поршень диаметром d п = 8 см перемещается со скоростью V п под действием силы F = 0,4 кН. Жидкость плотностью ρ = 870 кг/м 3 под действием поршня из правой части гидроцилиндра перемещается в бак, открытый в атмосферу. Определить скорость перемещения поршня V п, если высота h = 9,4 м.
Рис. 3.21. Схема к задаче 3.9.1
Плоскость сравнения — выбираем по оси гидроцилиндра. Сечение 1 — 1 выбираем по живому сечению жидкости в гидроцилиндре, причём параметры уравнения, относящиеся к этому сечению, относятся к центру тяжести сечения. Сечение 2 — 2 выбираем по свободной поверхности жидкости, где давление — только атмосферное (избыточное р изб = 0), скорость жидкости V 2 ≈ 0. Составим уравнение Бернулли, где давление будем учитывать в избыточной системе отсчёта .
Для сечения 1 — 1 :
— геометрическая высота z 1 = 0, так как центр тяжести сечения совпадает с плоскостью сравнения;
— избыточное давление создаётся силой 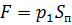
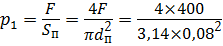
— жидкость в сечении движется с той же скоростью, что и поршень ( V 1 = V п), поэтому скоростной напор запишем как 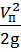
Для сечения 2 — 2 :
— геометрическая высота z 2 = h ;
— избыточное давление р 2 = 0;
Составим уравнение Бернулли:
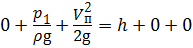
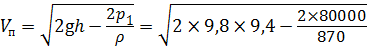
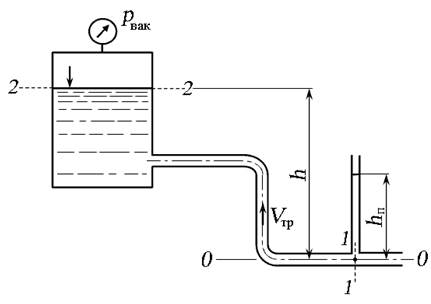
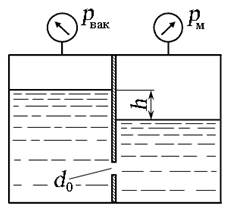
Задача 3.9.2. Определить вакуумметрическое давление в баке р вак, при котором скорость течения потока жидкости в трубопроводе составит V тр = 1,2 м/с. Высота h = 3,2 м, плотность жидкости ρ = 870 кг/м 3 . Высота уровня жидкости в пъезометре составляет h п = 0,64 м.
Рис. 3.22. Схема к задаче 3.9.2
Плоскость сравнения — выберем по оси трубопровода в нижней его части. Сечение 1 — 1 выберем по установленному в нижней части трубы пъезометру, сечение 2 — 2 выберем по свободной поверхности жидкости в баке. Составим уравнение Бернулли, где давление будем учитывать в избыточной системе отсчёта .
Для сечения 1 — 1 :
— геометрическая высота z 1 = 0, так как центр тяжести сечения совпадает с плоскостью сравнения;
— пъезометрическая высота в сечении 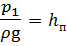
— скорость течения жидкости в трубопроводе V 1 = V тр.
Для сечения 2 — 2 :
— геометрическая высота z 2 = h ;
— вакуумметрическая высота 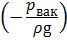
Составим уравнение Бернулли:
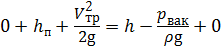
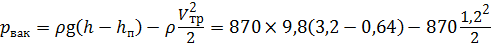
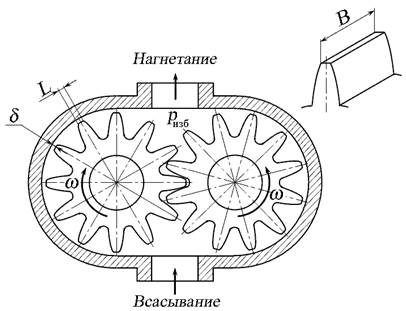
Задача 3.9.3. Определить утечки через радиальные зазоры в шестерённом насосе вследствие разности давлений в нагнетательной и всасывающей полости. Высота каждого зазора δ = 0,09 мм, длина зазора L = 2 мм, ширина В = 30 мм, перепад давлений ∆р = 1,32 МПа, наружный диаметр шестерни D = 62 мм, частота вращения n = 1450 об/мин, вязкость масла μ = 0,012 Па∙с.
Рис. 3.23. Схема к задаче 3.9.3
Считаем, что число зубьев, образующих радиальные зазоры слева и справа, одинаковы, и равны N = 7 с каждой стороны, размеры зазоров также одинаковы. Поэтому величина утечек слева и справа одинакова. Перепад давлений, приходящийся на один зазор, равен
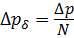
Общий расход через зазоры равен сумме расходов слева и справа
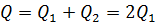
Расход через зазоры слева или справа равен согласно (3.18)
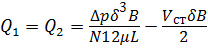
Окружная скорость 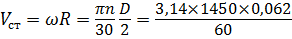
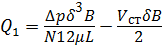
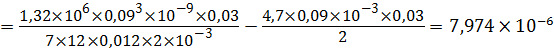
Общий расход через зазоры вследствие утечек
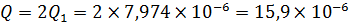
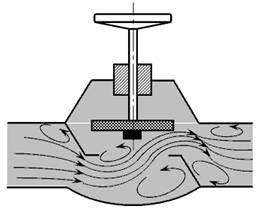
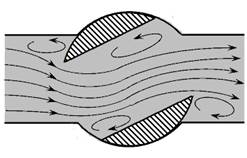
Потери напора в местных сопротивлениях зависят главным образом только от конструкции местного сопротивления . Например, при прохождении потока через вентильный кран образуется больше завихрений, следовательно, происходит больше потерь напора (энергии), чем при прохождении через пробковый кран (рис. 4.3).
Рис. 4.3. Вихреобразование при протекании жидкости:
а ) — в вентильном кране; б ) — в пробковом кране
Потери напора в местных сопротивлениях h м определяют по формуле Вейсбаха:
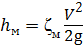
где ζм — коэффициент местного сопротивления.
Коэффициент ζм определяют опытным путём. В справочниках приведены полученные экспериментально значения коэффициентов для различных типов местных сопротивлений. Теоретически получена формула при внезапном расширении или сужении потока.
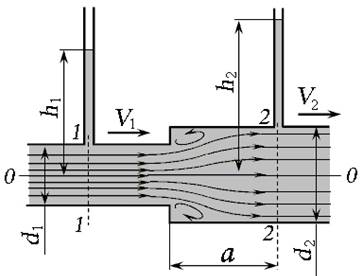
Рис. 4.4. Внезапное расширение потока
Особенностями внезапного расширения потока (рис. 4.4) являются:
— пъезометр в сечении 2 — 2 устанавливают на расстоянии а от зоны расширения для определения коэффициента ζвр (коэффициент сопротивления при внезапном расширении) опытным путём, так как действительная пъезометрическая высота будет только в безвихревой зоне трубопровода (в зоне сформированного основного потока);
— пъезометрическая высота в сечении 2 — 2 будет больше, чем в сечении 1 — 1 ( 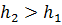
Для пояснения последнего утверждения составим уравнение Бернулли для сечений 1 — 1 и 2 — 2 относительно плоскости сравнения — для идеальной жидкости (то есть без учёта потерь напора), учитывая, что пъезометрическая высота 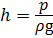
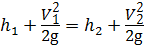
Так как скорость 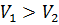
Потери напора h вр при внезапном расширении равны скоростному напору, соответствующему потерянной скорости (формула Борда):
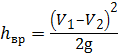
где ( V 1 – V 2) — потерянная скорость.
Используя уравнение неразрывности потока ( V 1 S 1 = V 2 S 2 =…= VnSn ), можно выразить V 1 через V 2 (или наоборот), после чего формула (4.12) примет вид:
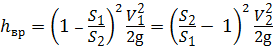
Отсюда видно, что коэффициент сопротивления при внезапном расширении потока, отнесённый к скорости V 1 или V 2 в соответствии с формулой (4.13), будет равен:
ζвр1 = 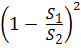
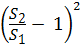

Учитывая, что потери напора рассматриваются в круглоцилиндрической трубе, формулу (4.14) можно переписать в виде:
ζ вр1 = 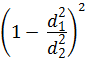
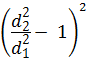
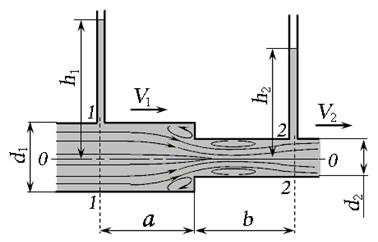
Особенностями внезапного сужения потока (рис. 4.5) являются:
— образование двух вихревых зон;
— для измерения пъезометрических напоров в сечениях пъезометры необходимо установить на расстоянии а и b от границы сужения (в зоне сформированного основного потока).
Рис. 4.5. Внезапное сужение потока
Коэффициент сопротивления ζвс при внезапном сужении трубы, отнесённый к скорости V 2 (скорость после сопротивления), определяют по формуле Идельчика:
ζвс = 0,5 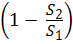
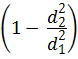
Для уменьшения сопротивления, связанного с расширением или сужением потока, применяют конусный переход от одного диаметра к другому.
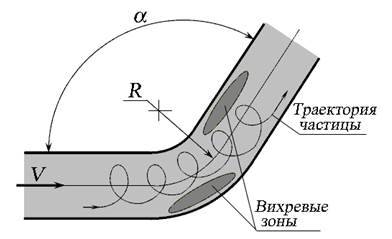
Рис. 4.6. Поворот трубопровода
Потери при повороте трубопровода зависят от угла поворота α и радиуса закругления R (рис. 4.6). Особенностью течения является поперечная циркуляция потока, в котором линии тока частиц становятся винтообразными.
Все гидроаппараты являются местными сопротивлениями. Для удобства расчётов потери напора в гидроаппаратах выражают в потерях давления ∆р , значение которого указывают в паспортных данных.
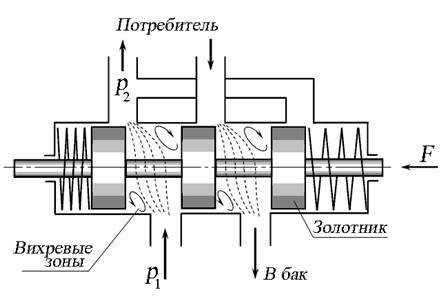
Рис. 4.7. Течение жидкости в гидрораспределителе
Рассмотрим течение жидкости через гидрораспределитель, основным элементом которого является золотник (рис. 4.7). Под действием пружин золотник занимает центральное положение, при котором гидролинии, подключённые к гидрораспределителю, перекрыты. Под действием внешней силы F золотник перемещается, открывая линии для течения жидкости. Образующиеся при этом завихрения жидкости снижают давление с р 1 до р 2. Уравнение Бернулли в этом случае примет вид:
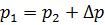
В большинстве случаев течение жидкости является турбулентным. При ламинарном режиме потери в местных сопротивлениях могут быть заданы эквивалентной длиной.
Эквивалентная длина L эк — это фиктивная длина, потери напора по которой будут равнозначны потерям в рассматриваемых местных сопротивлениях. Тогда общие потери напора определяют по формуле Пуазейля:
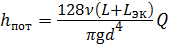
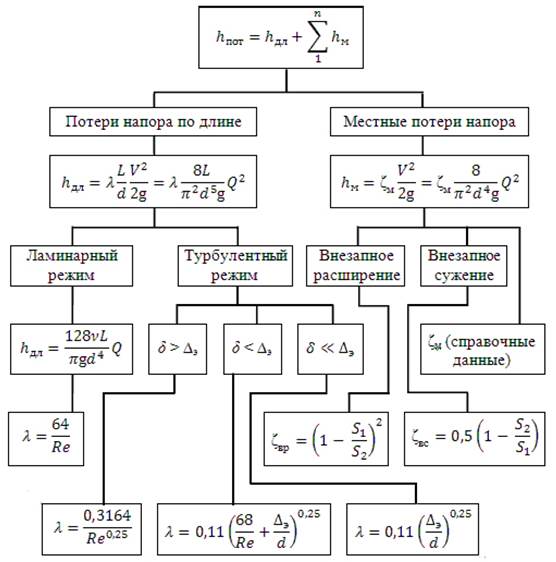
Структурная схема определения общих потерь напора в трубопроводе представлена на рис. 4.8.
Рис. 4.8. Структурная схема к определению потерь напора
по длине и в местных сопротивлениях
Примеры решения задач
Задачи данного раздела решают с помощью уравнения расхода и уравнения Бернулли для реальной жидкости с учётом потерь напора h пот. Необходимо помнить, что коэффициент Кориолиса для ламинарного течения жидкости равен α = 2, при турбулентном α = 1. Потери напора по длине зависят от коэффициента λ , который определяют в зависимости от соотношения толщины вязкого подслоя потока δ и эквивалентной шероховатости ∆ Э по формулам (4.6), (4.7) или (4.8). Для трубопроводов гидропривода используют формулу Блазиуса (4.6). Формулу Шифринсона (4.8) используют реже формулы Альтшуля (4.7), так как она предполагает значительный скоростной напор. Коэффициент внезапного расширения при втекании жидкости в бак ζ вр = 1, так как 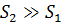
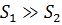
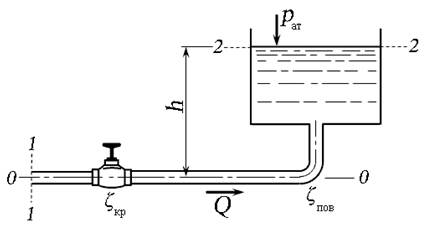
Задача 4.3.1. Вода под напором движется в бак, расположенный на высоте h от оси трубопровода. Определить высоту h до уровня воды в баке, открытом в атмосферу, если вязкость воды ν = 0,01 Ст, диаметр трубопровода d = 10 мм, длина L = 20 м, пъезометрический напор в сечении 1 — 1 принять H п = 20 м. Расход воды в трубопроводе составляет Q = 0,072 л/с. Коэффициенты сопротивления крана ζкр = 4, поворота ζпов = 1. Трубу считать гидравлически гладкой.
Рис. 4.9. Схема к задаче 4.3.1
Составим уравнение Бернулли для сечений 1 — 1 и 2 — 2 относительно плоскости сравнения — . Центр тяжести сечения 1 — 1 лежит в плоскости сравнения, поэтому z 1 = 0. Пъезометрический напор в сечении 1 — 1 является пъезометрической высотой в этом сечении:
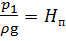
В сечении 2 — 2 скорость течения воды V 2 = 0, избыточное давление р изб = 0. Давления в сечениях определим в избыточной системе отсчёта. Коэффициент Кориолиса α = 1.
Потери напора h пот будут равны сумме потерь напора:
— по длине 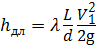
— местных сопротивлений 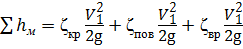
Учитывая, что ζвр = 1, сумма местных сопротивлений будет равна
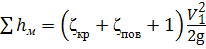
Скорость в трубопроводе определим из формулы расхода:
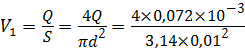
Определим коэффициент гидравлического трения λ по формуле Блазиуса (4.6):
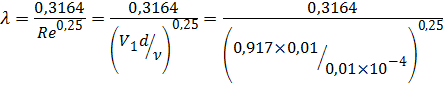
Уравнение Бернулли примет вид:
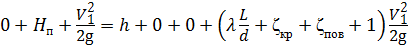
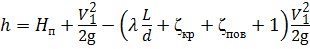
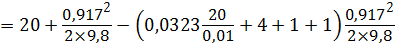
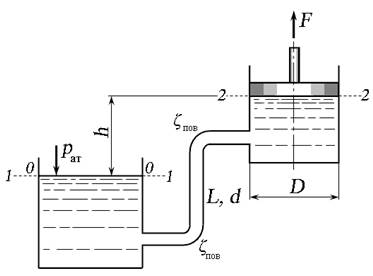
Задача 4.3.2. Поршень диаметром D = 200 мм движется равномерно вверх, всасывая воду. Диаметр трубопровода d = 50 мм, его длина L = 12 м, коэффициент гидравлического трения λ = 0,03, коэффициент местного сопротивления (поворота) ζпов = 0,5. При высоте h = 2 м сила, необходимая для перемещения поршня вверх, равна F = 2,35 кН.
Определить скорость перемещения поршня. Найти, до какой высоты hmax можно поднять поршень без возникновения кавитации, если давление насыщенного пара р нп = 4,25 кПа, плотность воды ρ = 1000 кг/м 3 . Атмосферное давление принять р ат = 98,7 кПа. Весом поршня и трением пренебречь.
Рис. 4.10. Схема к задаче 4.3.2
Составим уравнение Бернулли для сечений 1 — 1 и 2 — 2 , плоскость сравнения — и сечение 1 — 1 совпадают. Давления в сечениях определим в избыточной системе отсчёта.
В сечении 1 — 1 избыточное давление р изб = 0, скорость V 1 = 0. Движение жидкости примем турбулентным, коэффициент Кориолиса α = 1.
Под поршнем (в сечении 2 — 2 ) создаётся вакуумметрическое давление р вак, за счёт чего жидкость поднимается вверх. Давление р 2 = р вак будет определяться силой F и площадью поршня S п:
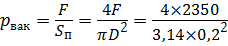
Потери напора h пот будут равны сумме потерь напора:
— по длине 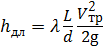
— местных сопротивлений 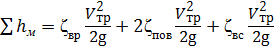
Учитывая, что ζвр = 1, ζвс = 0,5, сумма местных сопротивлений будет равна 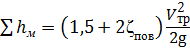
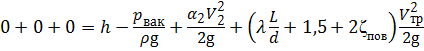
С помощью уравнения расхода выразим скорость в трубопроводе:
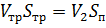
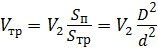
Подставим выражение для скорости V тр в составленное уравнение Бернулли:

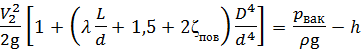
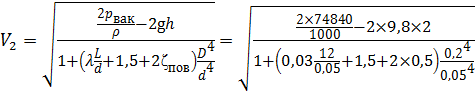
Наибольшую допустимую высоту подъёма поршня hmax определим из условия падения под поршнем абсолютного давления до давления насыщенного пара р нп. Составим уравнение Бернулли в абсолютных давлениях:
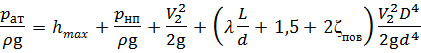
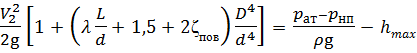
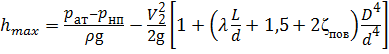
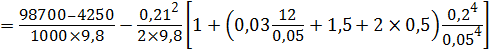
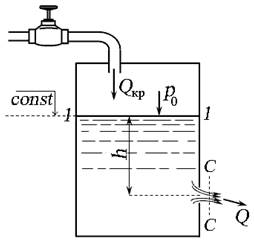
Рассмотрим истечение жидкости через отверстие диаметром d в стенке бака, расположенное на глубине h , в газовую среду. Свободная поверхность жидкости в баке находится под давлением р (рис. 5.1).
Рис. 5.1. Истечение жидкости из малого отверстия в атмосферу:
а ) — схема истечения; б ) — сжатие струи при истечении
Уровень жидкости в баке по плоскости 1 — 1 поддерживается постоянным (количество жидкости, вытекающей из крана Q кр, равно количеству жидкости Q , истекающей из отверстия в боковой стенке бака), то есть истечение происходит при постоянном напоре .
Скорости истечения на верхней и нижней границах истекающей из отверстия струи можно считать равными, если истечение происходит из малого отверстия.
Малым называется отверстие, если при истечении из него распределение скоростей в живом сечении струи можно считать равномерным. При этом должно выполняться условие:
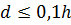
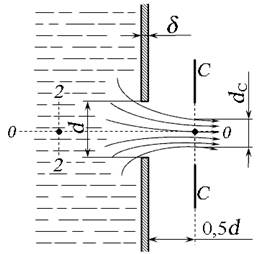
Боковая стенка не оказывает влияние на характер истечения, если толщина стенки не превышает половины диаметра отверстия ( δ ≤ 05 d ). В этом случае потери напора аналогичны потерям при внезапном сужении потока, а сама стенка будет называться тонкой .
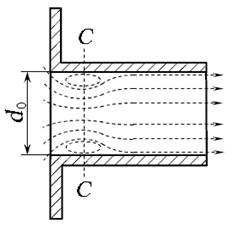
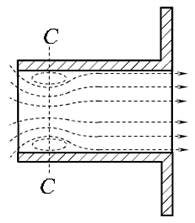
Частицы жидкости, приближаясь к отверстию, двигаются из всего близлежащего объёма по различным траекториям. Многие из них при попадании в отверстие должны изменить свою траекторию на 90º. Поскольку каждая частица имеет свою массу, то мгновенно изменить направление своего движения она не может. Следствием этого является сжатие струи жидкости при истечении (сечение С — С , рис. 5.1, б ). Формирование сжатого сечения струи диаметром d c заканчивается на расстоянии примерно 0,5 d .
Для оценки степени сжатия струи используют коэффициент сжатия ε (эпсилон), равный отношению площади струи в сжатом сечении S с к площади отверстия S . Для круглого отверстия:
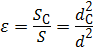
где S С и d С — площадь сжатого сечения и диаметр струи в сжатом сечении;
S и d — площадь и диаметр отверстия, через которое происходит истечение.
Для определения скорости истечения и расхода жидкости составим уравнение Бернулли для сечений 1 — 1 и С — С относительно плоскости сравнения — , проходящей через центр сжатого сечения:
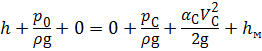
где р С — давление в сжатом сечении;
α С и V C — коэффициент Кориолиса и средняя скорость жидкости в сжатом сечении;
h м — местные потери напора при истечении.
Местные потери при истечении:
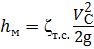
где ζт.с.— коэффициент потерь при истечении через отверстие в тонкой стенке.
С учётом (5.3) уравнение Бернулли (5.2) примет вид:
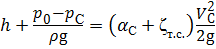
Выражение в левой части уравнения является гидростатическим напором Н ст, под действием которого происходит истечение:
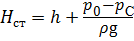
Тогда средняя скорость V С в сжатом сечении струи равна:
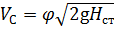
где φ — коэффициент скорости, 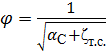
Коэффициент скорости φ отражает влияние распределения местных скоростей в сжатом сечении α С и потерь напора ζт.с..
Определим расход с учётом формулы (5.1):
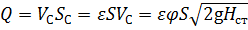
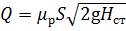
где μ р — коэффициент расхода, 
Если высоту столба жидкости h определить как 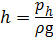
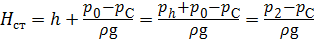
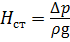
где ∆р — перепад давления (как правило, избыточного) до и после отверстия, под действием которого происходит истечение жидкости;
р 2 — давление в центре тяжести сечения 2 — 2 .
С учётом (5.5) уравнение для определения расхода жидкости при истечении из малого отверстия в тонкой стенке при постоянном напоре примет вид:
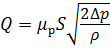
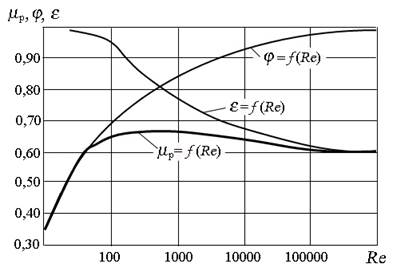
На рис. 5.2 показана зависимость коэффициентов расхода μ р, скорости φ и сжатия ε от числа Рейнольдса, подсчитанного для идеальной скорости истечения, то есть истечение при отсутствии сжатия струи и сопротивления. При числах Рейнольдса Re > 10 5 коэффициенты можно считать постоянными: ε = 0,64; φ = 0,97; μ р = 0,62.
Рис. 5.2. Зависимость коэффициентов расхода μ р, скорости φ и сжатия ε от числа Рейнольдса для круглого отверстия в тонкой стенке при полном совершенном сжатии
Согласно рис. 5.2, графики функций для определения коэффициентов μ р, φ и ε составлены для полного совершенного сжатия.
При полном сжатии происходит сжатие струи со всех сторон. Если же с одной или нескольких сторон сжатие отсутствует, сжатие струи будет неполным . Под с овершенным понимается такое полное сжатие, при котором отверстие достаточно удалено от ограничивающих поверхностей, и они не влияют на условия сжатия струи. Согласно опытным данным, это расстояние должно быть не менее 3 d для круглого отверстия, или утроенного соответствующего линейного размера — для прямоугольного.
При несовершенном сжатии, а тем более при неполном, коэффициенты истечения имеют бόльшие значения.
Рис. 5.3. Истечение через затопленное отверстие
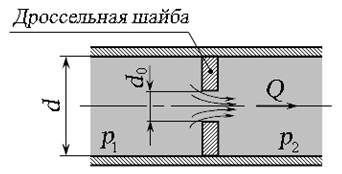
Большинство гидравлической аппаратуры работает по типу отверстий в тонкой или толстой стенке, где истечение происходит через затопленное отверстие. Например, по типу отверстия в тонкой стенке происходит истечение через дроссельную шайбу (рис. 5.3). Расход при истечении в жидкость определяют по формуле (5.6), что и для истечения в газообразную среду. Истечение через отверстие диаметром d происходит под действием перепада давлений 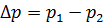
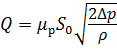
где S — площадь отверстия, через которое происходит истечение.
Истечение через насадки
Насадком называется короткая цилиндрическая или нецилиндрическая труба длиной L н = (3 … 5) d , присоединённая к отверстию (или отверстие в толстой стенке), работающая на выходе полным сечением. Различают насадки трёх типов — цилиндрические, конические и коноидальные. Рассмотрим истечение через цилиндрический насадок.
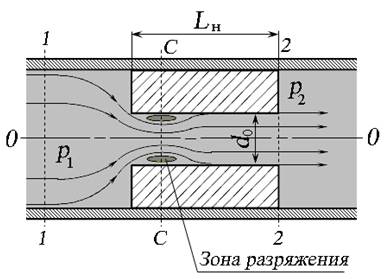
При входе в насадок струя сжимается, образуя сжатое сечение так же, как и при истечении через отверстие в тонкой стенке (сечение С — С , рис. 5.4). Затем струя постепенно расширяется до размеров отверстия, и выходит из насадка полным сечением. Такое движение жидкости в насадке называется безотрывным .
Рис. 5.4. Истечение через насадок
При истечении через насадок возникают следующие потери напора, отнесённые к скорости V 2 на выходе из насадка:
— такие же, как и при истечении через отверстие в тонкой стенке (от сечения 1 — 1 до сжатого сечения С — С )
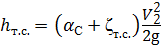
— местные потери, связанные с внезапным расширением потока от сечения С — С до живого сечения, в котором поток жидкости будет сформирован
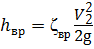
— потери напора по длине L н насадка диаметром d

Общие потери напора при истечении через насадок будут равны:
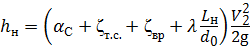
Составив уравнение Бернулли для сечений 1 — 1 и 2 — 2 , получим ту же формулу для определения скорости истечения на выходе из насадка, что и для истечения через отверстие в тонкой стенке:
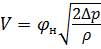
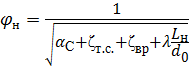
где V 2 = V — средняя скорость жидкости на выходе из насадка;
φ н — коэффициент скорости для истечения через насадок.
Расход жидкости при истечении через насадок определяют по той же формуле, что и для истечения через отверстия в тонкой стенке, но со своими коэффициентами скорости и расхода:
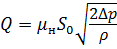
где μ н — коэффициент расхода при истечении через насадок, μ н = ε н φ н;
ε н — коэффициент сжатия струи, равный отношению площади S стр струи в живом сечении на выходе из насадка к площади S вых самого выходного отверстия насадка, ε н = 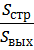
φ н — коэффициент скорости при истечении через насадок.
Коэффициенты μ н и φ н определены по результатам экспериментальных исследований.
В сжатом сечении возникает кольцевая зона разряжения, за счёт которых происходит подсос жидкости при истечении через насадок. В результате этого скорость жидкости при истечении через насадок больше, чем при истечении через отверстие в тонкой стенке.
Недостаток давления ( р ат – р вак) в зоне разряжения (в сжатом сечении) не должен быть меньше давления р нп насыщенного пара. В противном случае происходит нарушение сплошности потока жидкости, что приводит к нарушению нормальной работы насадка. Определим р вак, составив уравнение Бернулли для сечений С — С и 2 — 2 относительно плоскости сравнения — , совпадающей с осью насадка:
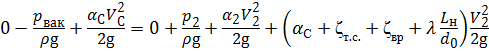
Учитывая, что α С = α 2 ≈ 1, V C = ε V 2, потери по длине примерно равны нулю, получим:
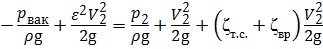
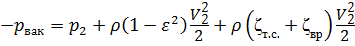
По формуле (5.8) 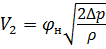
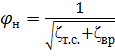

Коэффициент ζвр при внезапном расширении, отнесённый к скорости V 2, равен ζвр = 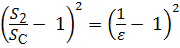
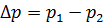
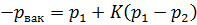
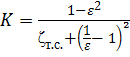
Для маловязких жидкостей (вода, бензин, керосин и т. д.) при значительных числах Рейнольдса (Re ≥ 10 5 ), при полном и совершенном сжатии коэффициент K ≈ 1. Тогда значение вакуумметрического давления р вак в сжатом сечении С — С :
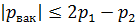
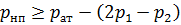
В случае, если 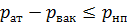
Цилиндрический насадок (рис. 5.5) может быть внешним или внутренним. Расход через внешний цилиндрический насадок будет несколько больше, чем через внутренний, так как коэффициент расхода для внешнего насадка μ внеш = 0,82, для внутреннего μ внутр = 0,71.
Рис. 5.5. Цилиндрический насадок:
а ) — внешний; б ) — внутренний
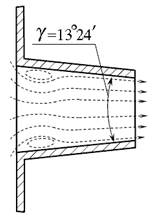
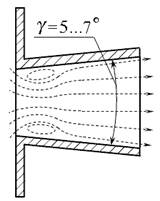
Нецилиндрические насадки могут быть конически сходящиеся, конически расходящиеся и коноидальные (рис. 5.6).
Рис. 5.6. Нецилиндрические насадки:
а ) — конически сходящиеся; б ) — конически расходящиеся;
Конически сходящиеся насадки имеют конусность γ = 13º24′, так как при таком значении конусности достигается максимальное значение коэффициента расхода μ к.с. = 0,94. При таком угле конусности площадь сжатого сечения примерно равна площади выходного отверстия насадка. Выходящая из конического насадка струя характеризуется большой кинетической энергией, в связи с чем эти насадки применяют в соплах турбин, гидромониторах и пожарных брандспойтах.
Конически расходящиеся насадки характеризуются бόльшим значением вакуума в сжатом сечении, чем в цилиндрическом. Такие насадки применяют, если необходимо пропустить относительно большой расход жидкости при малых скоростях на выходе.
Коноидальные насадки имеют сложную форму, за счёт которой на входе в насадок отсутствует вакуумметрическое давление, и такие насадки работают полным сечением при любом перепаде давлений. Коноидальный насадок обеспечивает наибольшую скорость в выходном сечении, следовательно, максимальную кинетическую энергию.
В табл. 3 приведены значения коэффициентов ε н, φ н и μ н для различных типов насадок.
Значения коэффициентов истечения через насадки
при совершенном сжатии
| Тип насадка | ε н | φ н | μ н |
| Внешний цилиндрический | 0,82 | 0,82 | |
| Внутренний цилиндрический | 0,707 | 0,707 | |
| Конически расходящийся (γ = 5 … 7º) | 0,45 … 0,5 | 0,45 …0,5 (по S вых) 1 … 1,05 (по S вх) | |
| Конически сходящийся (γ = 13º24′) | 0,98 | 0,96 | 0,94 |
| Коноидальные | 0,98 | 0,98 |
При воздействии струи жидкости на любую твёрдую преграду сила давления жидкости Р равна произведению гидродинамического давления на площадь действия. Для определения силы Р используют теорему количества движения — изменение количества движения ∆mV равно импульсу внешних сил ∆F, приложенных к выделенному участку потока :
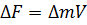
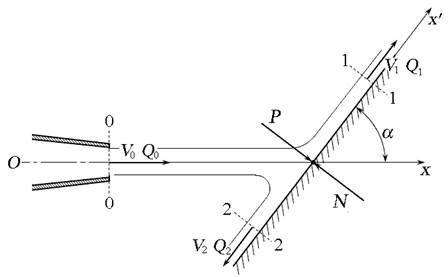
Рассмотрим неподвижную плоскую стенку, расположенную под углом α относительно оси струи (рис. 5.7). Струя жидкости вытекает из насадка площадью S с расходом Q и скоростью истечения V . Со стороны стенки возникает противодействующая сила N , равная силе давления жидкости Р и направленная в противоположную сторону:
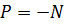
Рис. 5.7. Схема воздействия струи на твёрдую преграду
Изменение количества движения ( ∆mV ) за время dt в проекции на ось ОХ будет равно:
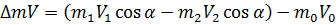
где 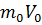
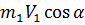
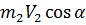
Импульс внешних сил за время dt равно 
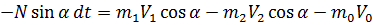
Учитывая, что 

Расход в сечении — за время dt равен сумме расходов в сечениях 1 — 1 и 2 — 2 :

Определим расходы в сечениях 1 — 1 и 2 — 2 . Для этого запишем уравнение количества движения относительно оси х′, проходящей по наклонной плоской стенке. Учитывая, что силы P и N направлены по нормали к выбранной оси х ′, проекция сил на эту ось будет равна нулю. Тогда:

откуда 
Используя уравнение равенства расходов, получим следующие значения расходов Q 1 и Q 2:
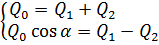
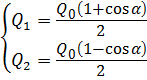
Подставим расходы Q 1 и Q 2 в уравнение (5.12), учитывая, что скорости в сечениях V = V 1 = V 2:
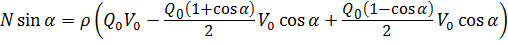
После математических преобразований получим:
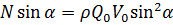
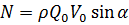
Учитывая, что 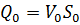
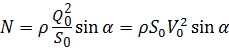
Если поверхность, на которую действует струя жидкости, движется в направлении движения жидкости со скоростью V пов, сила давления жидкости будет равна:
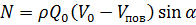
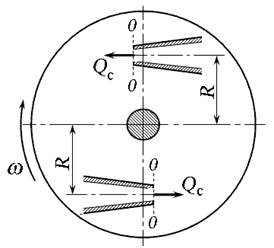
Рассмотрим реактивное действие струи, истекающей из сопла центробежного масляного фильтра (рис. 5.8).
Рис. 5.8. Схема двухсопловой центрифуги
с гидрореактивным приводом
Согласно теореме количества движения, реактивная сила при вращении вала фильтра согласно (5.16) с учётом α = 90º, 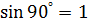
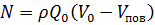
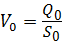
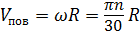
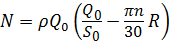
Вращающий момент на валу фильтра:
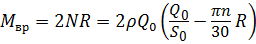
Учитывая, что расход масла Q , поступающего в центрифугу, равен 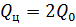
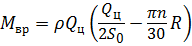
Примеры решения задач
Задачи на истечение решают без составления уравнения Бернулли с помощью основного выражения (5.4) или (5.6). При этом следует помнить, что гидростатический напор H ст определяется разностью давлений до и после отверстия. При расчёте истечения через насадки следует помнить, что коэффициенты истечения в отличие от истечения через отверстие определяют по табл. 3.
Задача 5.3.1. Определить расход и скорость истечения воды из малого круглого отверстия диаметром d = 3 см в боковой стенке резервуара больших размеров. Напор над центром отверстия h = 1 м, кинематическая вязкость воды при t = 20 ºС составляет ν = 10 -6 м 2 /с.
Определим число Рейнольдса, характеризующее истечение без учёта коэффициента скорости φ , то есть для истечения без образования сжатого сечения и сопротивления:
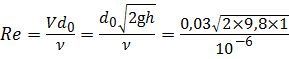
Из рис. 5.2 при Rе = 133 000 определим коэффициенты скорости φ и расхода μ р: φ = 0,98; μ р = 0,59. Тогда скорость истечения воды из малого отверстия в тонкой стенке в сжатом сечении будет равна:
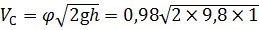
Расход вытекающей из отверстия воды будет равен:
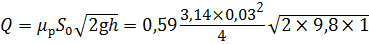
Задача 5.3.2. Определить расход жидкости, вытекающей из бака через отверстие площадью S = 0,01 см 2 . Показание ртутного манометра h рт = 268 мм, высота h = 2 м, коэффициент расхода отверстия μ р = 0,60. Плотность жидкости в баке ρ = 800 кг/м 3 , плотность ртути ρ рт = 13600 кг/м 3 . Атмосферное давление р ат = 0,1 МПа. Напор считать постоянным.
Определить, во сколько раз увеличится расход, если к отверстию присоединить цилиндрический внешний насадок, конически расходящийся насадок длиной L н = 5 d при угле конусности γ = 7º.
Расход жидкости определим по формуле (5.7):
Перепад давления ∆ р с верхней и нижней стороны отверстия определим в абсолютных единицах. Тогда ∆ р будет равен разности давления на дне сосуда (сумма р и весового давления 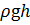
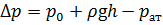
Рис. 5.7. Схема к задаче 5.3.2
Давление р (абсолютное давление) определим по показанию ртутного пъезометра, высота столба ртути в котором уравновесит избыточное давление, действующее по свободной поверхности жидкости в баке. Тогда абсолютное давление р будет равно:
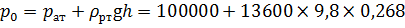
Тогда перепад давления:
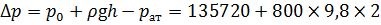
Расход жидкости через малое отверстие в тонкой стенке будет равен:
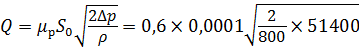
Определим расход жидкости при присоединении насадка к отверстию диаметром d , который равен 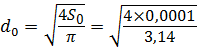
— цилиндрический внешний насадок ( μ внеш = 0,82)
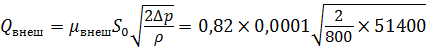
— конически расходящийся насадок ( μ к.р. = 0,5 по S вых)
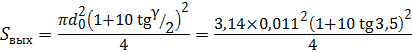
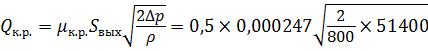
Определим, во сколько раз расход через насадки больше, чем через отверстие в тонкой стенке:
— через цилиндрический насадок 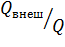
— через расходящийся насадок 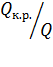
Задача 5.3.3. Определить направление истечения жидкости с плотностью ρ = 1000 кг/м 3 через отверстие диаметром d = 5 мм и расход, если разность уровней h = 2 м, показание вакуумметра соответствует 147 мм. рт. ст., показание манометра p м = 0,25 МПа, коэффициент расхода μ р = 0,62.
Рис. 5.8. Схема к задаче 5.3.3
Разность избыточного давления между баками равна:
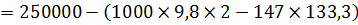
Поскольку давление в правой части бака больше, чем в левой, то направление течения жидкости будет направлено в левую часть емкости (ответ получили со знаком « », 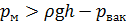
Тогда расход жидкости через отверстие с диаметром d будет равен:
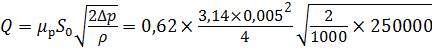
Задача 5.3.4. Определить диаметр отверстия дросселя d , установленного на сливе из гидроцилиндра, если шток цилиндра под действием внешней нагрузки F = 60 кН перемещается вправо со скоростью V = 20 см/с. Диаметры штока d ш = 40 мм, поршня D = 80 мм, коэффициент расхода дросселя μ р = 0,65, плотность жидкости ρ = 850 кг/м 3 , давление на сливе р с = 0,3 МПа.
Рис. 5.9. Схема к задаче 5.3.4
Определим избыточное давление в жидкости, которое создает сила F в правой части гидроцилиндра. Давление создаётся эффективной площадью поршня (эффективная площадь 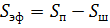
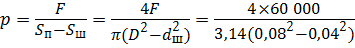
Перепад давлений на дросселе ∆ р будет равен:
∆ р = р – р с = 15,7 МПа.
Расход жидкости, протекающий через живое сечение дросселя рабочей площадью S со скоростью V др, будет равен расходу в цилиндре площадью S эф со скоростью V :
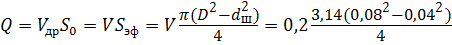
Площадь рабочего сечения дросселя S др будет равна:
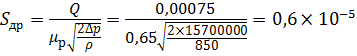
Тогда диаметр отверстия дросселя:
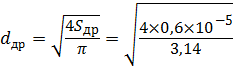
Трубопроводом называют систему напорных труб, предназначенных для перемещения разнообразных жидкостей и газов. Движение жидкости или газа по трубопроводу происходит в результате того, что напор в его начале больше, чем в конце.
Рис. 6.1. Создание напора с помощью:
а ) — насоса; б ) — давления газа; в ) — водонапорной башни;
г ) — разности высот уровней жидкости
Пъезометрический напор H п в трубопроводе может быть создан:
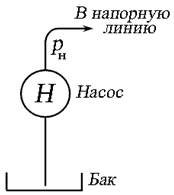
— за счёт работы насосов различного типа (рис. 6.1, а ), 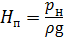
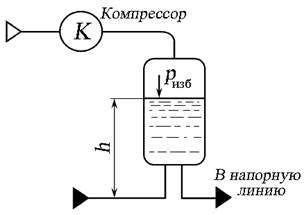
— избыточным давлением газа в резервуаре с жидкостью с помощью компрессора (рис. 1.6, б ), 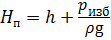
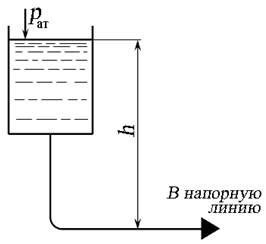
— использованием водонапорной башни (рис. 1.6, в ), 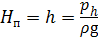
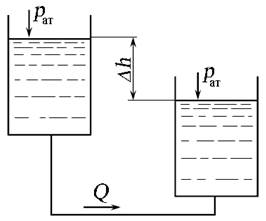
— за счёт разности высот уровней жидкости в сообщающихся сосудах (рис. 1.6, г ), 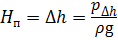
где ph и p∆h — избыточное давление, создаваемое высотой столба жидкости h и ∆h соответственно.
В зависимости от компоновки и технического расположения трубопроводы подразделяют на простые и сложные.
Простым называется трубопровод без ответвлений, состоящий из труб одного диаметра. Простой трубопровод разделяют на короткий и длинный. К длинным относят трубопроводы значительной протяжённости, в которых потери напора по длине являются основными, а местные потери напора составляют не более 10 % от общих потерь. К таким трубопроводам относят магистральные трубопроводы, газопроводы, трубопроводы гидротехнических сооружений.
В технических гидроприводах (например, станочные гидроприводы, гидроприводы автомобильных систем) применяют короткие трубопроводы, в которых местные потери соизмеримы с потерями по длине.
Сложным называется трубопровод, состоящий из труб разного диаметра, соединённых последовательно, параллельно или разветвлено.
Рассмотрим простой трубопровод, в котором напор создан избыточным давлением р 1 в сечении 1 — 1 (рис. 6.2).
Рис. 6.2. Схема к определению потребного напора
Составим уравнение Бернулли для сечений 1 — 1 и 2 — 2 относительно произвольно выбранной плоскости сравнения — :
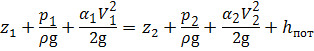
Трубопровод не меняет своего диаметра, поэтому V 1 = V 2 = V . Принимаем течение жидкости в трубопроводе турбулентным, коэффициент Кориолиса α 1 = α 2 = 1. Геометрическую высоту поднятия жидкости в трубопроводе обозначим как геометрический напор H г:
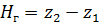
Тогда уравнение (6.1) примет вид:
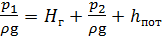
Сумма 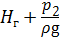
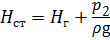
Потери напора h пот выразим через расход Q (п. 4.1, 4.2):
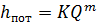
где m — показатель степени ( m = 1 при ламинарном течении, m = 2 при турбулентном течении);
K — величина сопротивления трубопровода.
Параметр K является размерной величиной, и для турбулентного режима равен:
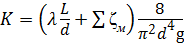
Пъезометрический напор 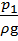
Потребный напор H потр — это пъезометрический напор, затрачиваемый на создание гидростатического напора H ст при заданном расходе Q :
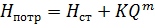
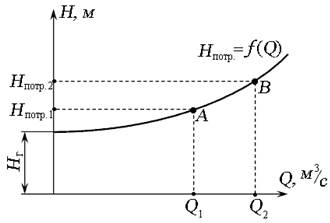
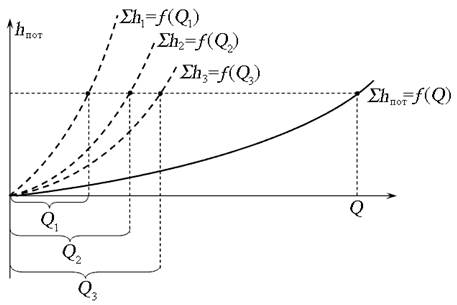
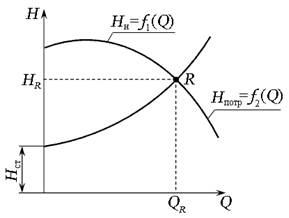
Используя выражение (6.3), можно построить графическую зависимость 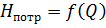
Рис. 6.3. Кривая потребного напора
Зависимость потерь напора h пот от расхода Q называют гидравлической характеристикой трубопровода :
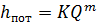
При ламинарном режиме гидравлическая характеристика трубопровода и кривая потребного напора представляют собой прямую линию ( m = 1), при турбулентном течении — параболу второй степени ( m = 2).
Последовательным называют сложный трубопровод, в котором жидкость течёт по последовательно соединённым простым трубопроводам разного диаметра (рис. 6.4).
Рис. 6.4. Схема последовательного соединения простых трубопроводов
При последовательном соединении трубопровода расход Q по всей его длине одинаков, потери напора равны сумме потерь на отдельных участках трубопровода:
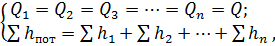
где n — количество участков трубопровода.
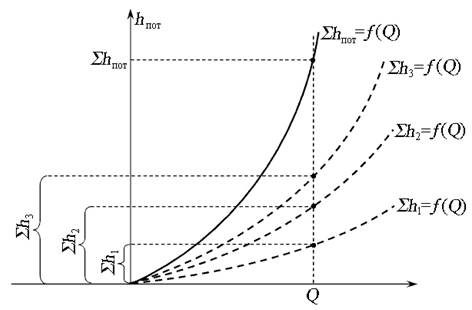
Такие трубопроводы удобнее всего рассчитывать, пользуясь гидравлической характеристикой трубопровода (рис. 6.5). Сложный трубопровод разбивают на ряд простых трубопроводов, для каждого простого трубопровода в одной системе координат строят свою гидравлическую характеристику. Так как расход для всех простых трубопроводов одинаков, а потери напора суммируются, производят сложение характеристик трубопроводов по оси ординат. Полученная в результате сложения графическая характеристика является характеристикой всего сложного трубопровода, состоящего из нескольких простых трубопроводов.
Рис. 6.5. Гидравлическая характеристика последовательного соединения простых трубопроводов для турбулентного режима течения жидкости
Параллельное соединение трубопровода
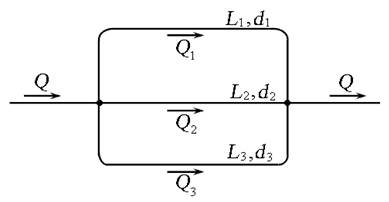
Параллельным называют сложный трубопровод, имеющий в начале общую точку разветвления, в конце общую точку соединения (рис. 6.6).
Рис. 6.6. Схема параллельного соединения простых трубопроводов
В таком трубопроводе расходы жидкости Q 1, Q 2, Q 3 … Qn распределяются таким образом, что гидравлические потери во всех параллельных линиях одинаковы:
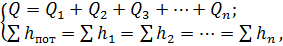
где Q — расход в точке разветвления и в точке соединения;
n — количество разветвлений.
Для построения общей гидравлической характеристики сложного трубопровода в одной системе координат строят характеристики для каждого простого трубопровода. Так как потери напора в трубопроводах равны, а суммируются расходы, сложение производят по оси абсцисс (рис. 6.7).
Рис. 6.7. Гидравлическая характеристика параллельного соединения
простых трубопроводов для турбулентного режима течения жидкости
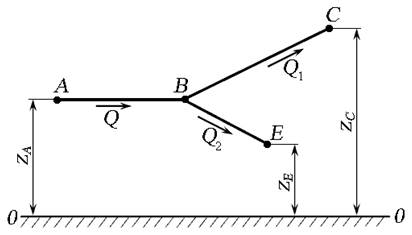
Разветвлённым называется сложный трубопровод, состоящий из нескольких простых трубопроводов, имеющих одну точку разветвления (рис. 6.8). Расчёт такого трубопровода выполняют как аналитическим методом, так и графоаналитическим.
Рис. 6.8. Схема разветвлённого соединения простых трубопроводов
Для определения параметров разветвлённого трубопровода его разбивают на ряд простых. Для каждого из трубопроводов составляют уравнение Бернулли относительно общей плоскости сравнения — , сечения выбирают в начале трубопровода (точка А ) в конечных точках (точки С и Е ), и в точке разветвления (точка В ). Пъезометрический напор в точке В разветвления трубопровода будет одинаков для всех простых трубопроводов .
Составим уравнение Бернулли для сечений В и Е :
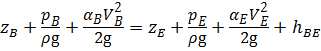
Так как трубопровод ВЕ простой, диаметры, а следовательно, скорости течения жидкости в сечениях В и Е одинаковы ( V B = V A). Сумма геометрической и пъезометрической высоты есть статический напор в сечении В и Е :

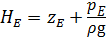
Тогда уравнение (6.7) с учётом того, что 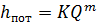
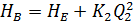
Составив по аналогии уравнения для трубопроводов АВ и ВС , получим систему уравнений:
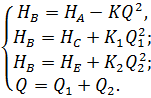
Решая совместно систему уравнений (6.8) при необходимых известных параметрах трубопровода (геометрические параметры трубопровода и давления в сечениях), можно определить неизвестный параметр (например, расходы Q 1 и Q 2 в разветвлениях).
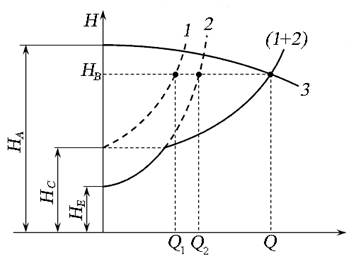
Рис. 6.9. Гидравлическая характеристика разветвлённого соединения
трубопровода для турбулентного режима течения жидкости:
1 — зависимость пъезометрического напора в точке В от расхода в трубопроводе ВС ; 2 — зависимость пъезометрического напора в точке В от расхода в трубопроводе ВЕ ; 3 — зависимость пъезометрического напора в точке В от расхода в трубопроводе АВ ; (1 2) — зависимость пъезометрического напора в точке В от суммарного расхода в трубопроводе ВС и ВЕ ; R — точка пересечения графических характеристик 3 и ( 1 2 ), координаты которой соответствуют полному расходу Q в трубопроводе и напору НВ
Для графоаналитического решения необходимо построить кривую потребного напора разветвлённого трубопровода. Для определения основных параметров трубопровода необходимо выполнить следующие действия (рис. 6.9):
— построить кривые потребного напора для каждого простого трубопровода (кривые 1 и 2 );
— произвести графическое сложение кривых 1 и 2 по оси абсцисс (расхода) — по принципу сложения графиков функций для параллельного трубопровода;
— точка пересечения R суммарной графической характеристики ( 2 3 ) трубопроводов, отходящих от точки разветвления, и графической характеристики подводящего трубопровода, даёт значение расхода Q и напора HB в точке разветвления;
— точки пересечения горизонтальной прямой, проведённой из точки R , и кривых 1 и 2 (точки R 1 и R 2), дают значения расходов Q 1 и Q 2 в разветвлениях.
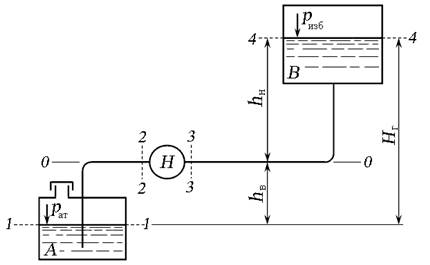
Для технических гидросистем основным способом принудительного движения жидкости является применение насоса. Рассмотрим простой трубопровод, в котором насос Н подаёт жидкость из приёмного бака А в напорный бак В (рис. 6.10). Трубопровод, идущий от насоса, называют напорным . Трубопровод, по которому насос всасывает жидкость, называют всасывающим .
Рис. 6.10. Трубопровод с насосной подачей жидкости
Составим уравнение Бернулли для сечений 3 — 3 и 4 — 4 относительно плоскости сравнения — , совпадающей с горизонтальной осью насоса. Учтём, что на выходе (сечение 3 — 3 ) из насоса создаётся избыточное давление, скорость течения жидкости в баке В (сечение 4 — 4 ) примерно равна нулю ( V 4 ≈ 0), давление на свободной поверхности жидкости в баке В — избыточное. Течение жидкости будем считать турбулентным, поэтому коэффициент Кориолиса для всего трубопровода α = 1. Диаметры напорного и всасывающего трубопроводов примем равными, поэтому V 1 = V 2 = V 3 = V . Тогда уравнение Бернулли примет вид:
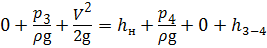
где h н — высота нагнетания жидкости насосом в напорном трубопроводе;
h 3-4 — потери напора в напорном трубопроводе.
Составим уравнение Бернулли для всасывающего трубопровода для сечений 1 — 1 и 2 — 2 относительно той же плоскости сравнения. Давление на свободной поверхности жидкости в баке А атмосферное. Давление в сечении 2 — 2 на входе в насос будет избыточным. Тогда уравнение Бернулли для давлений в избыточной системе отсчёта примет вид:
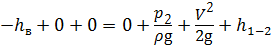
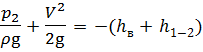
где h в — высота всасывания жидкости насосом.
h 1-2 — потери напора во всасывающем трубопроводе.
Знак «–» при определении давления на входе в насос указывает на вакуумметрическое давление.
Полная удельная энергия жидкости в трубопроводе:
— на выходе из насоса (6.9) 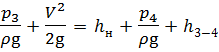
— на входе в насос (6.10) 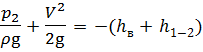
Приращение удельной энергии жидкости в насосе для единицы её веса называется напором насоса Н н:
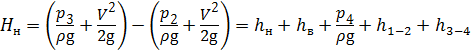
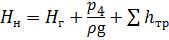
где Н г — полная высота подъёма жидкости насосом, называемая геометрической высотой ( 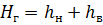
Сумма геометрической и пъезометрической высоты есть статический напор:
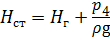
Потери напора выразим через расход:
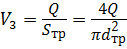
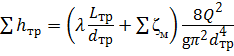
Тогда напор насоса будет равен:
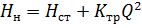
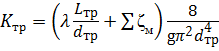
где K тр — величина сопротивления всего трубопровода.
Формула (6.11) для определения напора насоса Н н для подачи жидкости на статическую высоту Н ст и преодоление гидравлических потерь, идентична формуле потребного напора трубопровода (6.4):
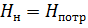
На полученном равенстве основан метод расчёта насосного трубопровода, который заключается в построении на одном графике напорной характеристики насоса 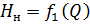
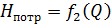
Напор насоса Н н является функцией его объёмной подачи, то есть объёма подаваемой жидкости в единицу времени — расхода Q .
Графическое нахождение рабочей точки для турбулентного режима течения жидкости с насосной подачей изображено на рис. 6.11.
Рис. 6.11. Графическое нахождение рабочей точки для турбулентного режима течения жидкости с насосной подачей:
Н ст — статический напор; 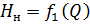
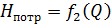
Кавитационный расчёт насоса
Для любого насоса возникновение кавитации во всасывающем патрубке приводит к ухудшению характеристик насоса, в частности, значительному снижению напора и к разрушению рабочих органов насоса. Для предупреждения возникновения кавитации абсолютное давление во входном патрубке насоса должно быть не ниже давления насыщенного пара р нп. Так как давление р нп является величиной абсолютной, а давление во входном патрубке ниже атмосферного на величину вакуумметрического давления, можно записать условие, при котором будет обеспечиваться нормальная работа насоса:
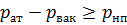
где р вак — вакуумметрическое давление на входе в насос;
р нп — давление насыщенного пара при данной температуре.
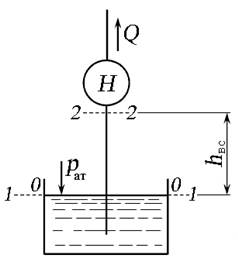
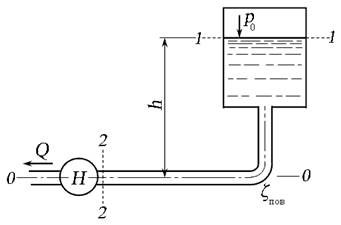
Рассмотрим насос, расположенный на высоте h вс от свободной поверхности жидкости (рис. 6.12). Составим уравнение Бернулли для сечений 1 — 1 и 2 — 2 относительно плоскости сравнения — , совпадающей со свободной поверхностью жидкости в резервуаре. Уравнение составим для давлений в абсолютной системе отсчёта, течение жидкости будем считать турбулентным ( α = 1), скорость на входе в насос в сечении 2 — 2 обозначим как V вс — скорость потока жидкости во всасывающем патрубке насоса:
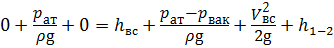
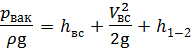
где h вс — высота всасывания;
h 1-2 — потери напора во всасывающем трубопроводе;
L и d — длина и диаметр всасывающего трубопровода.
Рис. 6.12. Схема всасывающего трубопровода
Согласно (6.14), вакуумметрическая высота Н вак во всасывающем патрубке насоса определяется суммой всасывающей высоты, удельной кинетической энергией (скоростного напора) потока и гидравлических потерь во всасывающем трубопроводе:

Вакуумметрическое давление р вак во входном патрубке насоса не должно превышать критического вакуумметрического давления р вак.кр, при котором возможно возникновение кавитации:
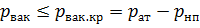
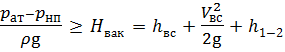
Выражение 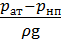
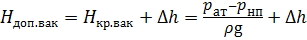
где H доп.вак — допустимая вакуумметрическая высота;
∆h — кавитационный запас.
Критическую вакуумметрическую высоту, при которой возникает кавитация в жидкости, определяют по результатам кавитационных испытаний насоса. Кавитационный запас ∆h составляет 20 … 30 % от критической вакуумметрической высоты:
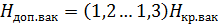
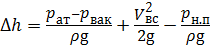
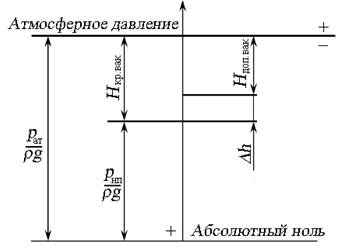
Взаимосвязь высот Н кр.вак, Н доп.вак и кавитационного запаса ∆h представлена на рис. 6.13.
Рис. 6.13. Схема к определению высот Н кр.вак, Н доп.вак, ∆h
Согласно выражению (6.14), вакуумметрическое давление во входном патрубке насоса зависит от высоты всасывания, диаметра трубопровода и гидравлических потерь:
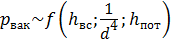
Предельная высота всасывания h вс указывается в паспортных данных насоса. Для гидроприводов автомобильной техники и машиностроительных гидроприводов характерно расположение насоса в баке, или бак располагают таким образом, что уровень жидкости в баке будет выше входного отверстия в насос. На свободной поверхности жидкости в баке может быть создано избыточное давление.
Так как давление р вак на входе в насос обратно пропорционально диаметру входного патрубка в четвёртой степени, диаметр входного отверстия в насос, как правило, больше выходного отверстия. Увеличение диаметра на входе приводит к снижению скорости течения жидкости и снижению значения вакуумметрического давления.
Для технических гидроприводов характерна малая длина всасывающего трубопровода, поэтому гидравлические потери по длине малы и практически не оказывают влияния на работу гидропривода. Местные сопротивления могут оказывать значительное влияние. В частности, установка фильтра может быть причиной значительного вакуумметрического давления. Поэтому на входе в насос устанавливают, как правило, фильтры грубой очистки.
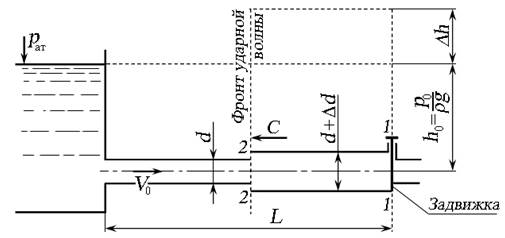
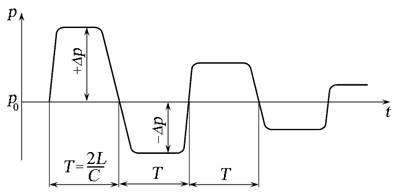
При быстром закрытии запорного устройства (например, задвижки или клапана) в напорном трубопроводе происходит резкое повышение давления, связанное с уменьшением скорости движения жидкости до нуля, и преобразованием кинетической энергии потока в потенциальную. Схема гидравлического удара в трубопроводе приведена на рис. 6.14. Жидкость по трубопроводу длиной L и диаметром d движется со скоростью V , избыточное давление в трубопроводе р определяется высотой столба жидкости h в резервуаре, открытом в атмосферу.
При быстром закрытии затвора давление в трубопроводе повысится на величину ∆р . В результате жидкость будет сжиматься, диаметр трубопровода в результате деформации увеличится до значения d ∆d . В трубопроводе образуется фронт ударной волны с давлением р ∆р , перемещающейся от затвора к резервуару со скоростью С .
Рис. 6.14. Схема гидравлического удара в трубопроводе:
За фронтом ударной волны происходит выравнивание давления и скорости потока, направленного в обратную сторону — к резервуару, до начальных значений р и V , стенки трубопровода и жидкость возвращаются в первоначальное состояние.
Так как жидкость движется от задвижки, происходит понижение давления на величину (– ∆р ), расширение жидкости и сжатие трубопровода. После достижения фронтом волны резервуара происходит движение в прямом направлении (к задвижке) со скоростью V и давлением р . При достижении задвижки возникает ситуация, соответсвующая начальноиу моменту при закрытии затвора.
В связи с упругими свойствами жидкости и материала стенок трубопровода, а также гидравлическими потерями на трение процесс носит затухающий характер (рис. 6.15).
Рис. 6.15. Циклограмма изменения давления при гидравлическом ударе
Время цикла, при котором происходит повышение и уменьшение давления на величину ∆р , называется фазой гидравлического удара T :
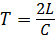
где L — длина трубы, по которой перемещается фронт ударной волны;
С — скорость перемещения ударной волны.
Если время закрытия задвижки t з T , то есть трубопровод перекрывается практически мгновенно, происходит так называемый прямой гидравлический удар .
В этом случае повышение давления определяют по формуле Жуковского:
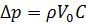
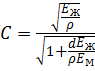
где Е ж и Е м — модуль упругости жидкости и материала трубопровода;
d — диаметр трубопровода.
Если время закрытия задвижки t з > T , в момент возвращения ударной волны через не перекрытую часть живого сечения потока успевает пройти некоторый расход жидкости со скоростью V . Кинетическая энергия потока уменьшается по сравнению с прямым ударом, и потенциальная энергия станет меньше. Такой гидравлический удар называют непрямым гидравлическим ударом . В этом случае формула Жуковского преобразуется к виду:
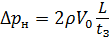
где ∆р н — повышение давления в трубопроводе при непрямом гидроударе;
t з — время перекрытия живого сечения трубопровода.
При непрямом гидравлическом ударе величина ∆р н не зависит от скорости С распространения ударной волны. Таким образом, чтобы уменьшить повышение давления в трубопроводе, необходимо увеличить время закрытия задвижки или клапана, перекрывающего живое сечение потока в трубопроводе.
Примеры решения задач
Для сложного трубопровода, состоящего из n -го количества участков, справедливы следующие равенства:
— для последовательного соединения трубопровода (6.5)
— для параллельного соединения трубопроводов (6.6)
На равенствах (6.5) и (6.6) основан способ определения параметров сложного трубопровода — напора, расхода и геометрических параметров трубопровода. Неизвестные параметры трубопровода могут быть определены аналитически или графоаналитически, построением характеристики сложного трубопровода. Для этого необходимо выполнить следующие действия:
— представить сложный трубопровод в виде соединения простых участков;
— для каждого простого участка составить уравнение потребного напора (6.4) или гидравлическую характеристику трубопровода (6.5)
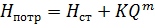
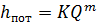
С достаточной точностью можно принять:
— для ламинарного режима
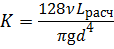
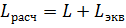
где L экв — длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе;
— для турбулентного режима
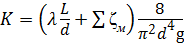
При аналитическом определении неизвестных параметров трубопровода составляют систему уравнений, где количество неизвестных не превышает количество уравнений, например, система уравнений для разветвлённого трубопровода (6.8).
При графоаналитическом определении неизвестных параметров необходимо построить характеристику сложного трубопровода. Для этого необходимо:
— рассчитать и построить характеристики каждого простого участка трубопровода;
— провести графическое сложение характеристик последовательных участков по оси расхода, или сложение характеристик параллельных участков по оси напора (оси ординат).
Для разветвлённого трубопровода сложение характеристик проводят по правилу сложения характеристик параллельного трубопровода.
Задачи на расчёт простого трубопровода можно разбить на три типа:
Первый тип. Даны:
— расход жидкости Q в трубопроводе;
— все геометрические размеры (длина L , диаметр d и геометрическая высота h );
— эквивалентная шероховатость труб ∆ Э;
— давление или напор в конечном сечении (для всасывающих трубопроводов — в начальном);
— параметры жидкости (плотность ρ и кинематическая вязкость ν ).
Местные сопротивления либо заданы коэффициентами ζм или эквивалентными длинами L экв, либо оцениваются по справочным данным.
Требуется найти потребный напор Н потр.
В этом случае задачу решают в следующей последовательности:
— по известным значениям Q , d и ν находят число Рейнольдса Rе и определяют режим течения жидкости;
— при ламинарном режиме течения искомый напор определяют по формуле (6.4), где коэффициент K определяют по формуле для ламинарного режима;
— при турбулентном режиме задачу решают по той же формуле (6.4), где коэффициент K определяют по формуле для турбулентного режима. Коэффициент λ определяют по соответствующим формулам (4.6), (4.7) или (4.8) в зависимости от соотношения толщины вязкого подслоя потока δ и размера эквивалентной шероховатости ∆ Э.
Второй тип . Даны: напор Н расп, который будем называть р асполагаемым , так как он известен, и все величины, перечисленные в первом типе задач, кроме расхода Q . Так как число Рейнольдса в данной задаче определить нельзя, то необходимо выразить расход Q через критическое число Рейнольдса Rе = 2300 и определить Н кр, соответствующее смене режима. Сравнив Н кр и Н расп, можно легко определить режим течения.
При ламинарном режиме задача решается просто, как и в задаче первого типа. При турбулентном режиме задача решается по формулам (6.3) и (6.4).
В уравнении (6.4) содержатся два неизвестных — расход Q и коэффициент λ т, зависящие от числа Рейнольдса. Для решения задачи задают значение коэффициента λ т с учётом шероховатости и определяют его по формуле Альтшуля при Rе → 
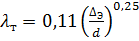
Значение коэффициента λ т изменяется в небольших пределах (λт = 0,015 … 0,045).
Затем, решая уравнение (6.4), находят расход Q в первом приближении. По найденному расходу Q определяют Rе в первом приближении, а по Rе — уже более точное значение λ т. Обычно бывает достаточно второго приближения.
Для решения этой же задачи графическим способом строят кривую потребного (располагаемого) напора для данного трубопровода с учётом переменности λ т, то есть для ряда значений Q подсчитывают V , Rе , λ т и Н потр. Затем, построив кривую Н потр = f ( Q ), и зная ординату Н потр = Н расп, находят соответствующую ей абсциссу, то есть находят расход Q .
Третий тип. Даны: расход Q , располагаемый напор Н расп, и все величины, перечисленные ранее, кроме диаметра трубопровода d , который и нужно определить.
Так как число Рейнольдса определить нельзя, то выражают диаметр через критическое число Рейнольдса Rе = 2300 и определяют Н кр, соответствующее смене режима движения жидкости. Сравнивая Н кр и Н расп, определяют режим течения.
При ламинарном режиме задача решается просто по соответствующим формулам.
При турбулентном режиме задачу решают графически. При этом задаются рядом значений диаметра d , по которым подсчитывают Н потр. Затем строят график Н потр= f ( d ) и по нему, зная Н расп, определяют диаметр d .
Задача 6.8.1. На рисунке показан всасывающий трубопровод гидросистемы. Длина трубопровода L = 1 м, диаметр d = 20 мм, расход жидкости Q = 0,314 л/с, абсолютное давление воздуха на свободной поверхности жидкости в баке р = 100 кПа, высота h = 1 м, плотность жидкости (масло индустриальное при 25°С) ρ = 900 кг/м 3 . Коэффициент сопротивления поворота ζпов = 0,42.
Определить абсолютное давление перед входом в насос при температуре рабочей жидкости t 1 = 25°С ( ν = 0,2·10 -4 м 2 /с). Определить, как изменится искомое давление в зимнее время, когда при этом же расходе температура жидкости упадет до t 2 = –35°С ( ν = 10·10 -4 м 2 /с).
Рис. 6.16. Схема к задаче 6.8.1
Определим скорость течения жидкости в трубе V 2 из уравнения расхода (3.2):
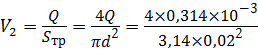
Определим число Рейнольдса (3.15):
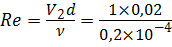
Режим движения жидкости ламинарный ( Re α = 2), поэтому потери по длине h дл определим по формуле Пуазейля (4.5):
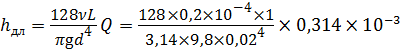
Потери в местных сопротивлениях определим по формуле Вейсбаха (4.10). Для местных потерь напора при втекании в бак (внезапное сужение ζвс = 0,5, так как 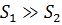
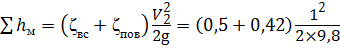
Общие потери напора
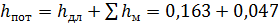
Составим уравнение Бернулли для сечений 1 — 1 и 2 — 2 , проведя плоскость сравнения — по оси горизонтального участка трубы, откуда выразим абсолютное давление р 2 перед входом в насос:
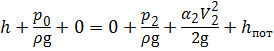
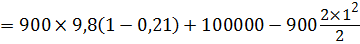
Подсчитаем потери по длине при t 2 = –35°С:
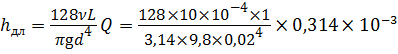
Общие потери напора 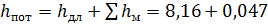
Тогда искомое давление при при t 2 = –35°С:
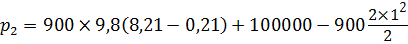
Давление на входе в сечении 2 — 2 ниже атмосферного на давление вакуума р вак = р 2 – р ат = 28540 – 100000 = 71,46 кПа.
Задача 6.8.2. По трубопроводу диаметром d = 10 мм и длиной L = 10 м подаётся жидкость вязкостью ν = 0,0001 м 2 /с под действием перепада давления ∆ р = 4 МПа, плотность жидкости ρ = 1000 кг/м 3 . Определить режим течения жидкости в трубопроводе.
Определим расход жидкости в трубопроводе. Поскольку потери в трубопроводе будут равны разности пъезометрических высот, то с учётом формулы Пуазейля (4.5):
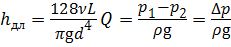
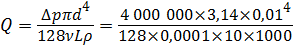
Теперь определим критический расход Q кр при критическом значении числа Рейнольдса Rе = 2300:
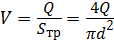
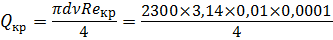
Поскольку Q Q кр, значит, режим течения жидкости — ламинарный.
Задача 6.8.3. Определить потребный напор Н потр, который необходимо создать в сечении — для подачи в бак воды плотностью ρ = 1000 кг/м 3 и вязкостью ν = 0,0157 Cт, если длина трубопровода L = 80 м, его диаметр d = 50 мм, расход жидкости Q = 15 л/с, высота h = 30 м, избыточное давление в баке р = 0,2 МПа, коэффициент сопротивления крана ζкр = 5, поворота ζпов = 0,8, эквивалентная шероховатость внутренних стенок трубы ∆Э = 0,04 мм. Внутреннюю поверхность трубы считать гидравлически шероховатой.
Рис. 6.17. Схема к задаче 6.8.3
Составим уравнение Бернулли для сечений — и 1 — 1 относительно плоскости сравнения, совпадающего с сечением — :
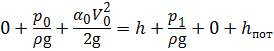
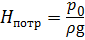
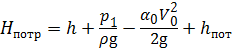
Определим число Рейнольдса, воспользовавшись уравнениями (3.15) и (3.2):
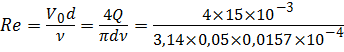
Поскольку режим течения турбулентный ( α = 1), то потери напора по длине определим по формуле Дарси — Вейсбаха (4.3):
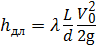
Для определения потерь напора по длине определим скорость V течения жидкости и коэффициент гидравлического трения λ :
— скорость течения жидкости 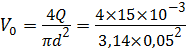
— коэффициент λ по формуле Альтшуля (4.7)
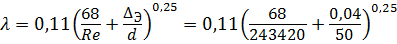
Тогда потери по длине 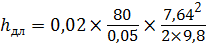
Местные потери напора (с учетом внезапного расширения ζр = 1) будут равны:
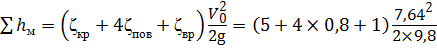
Общие потери напора
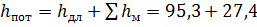
Тогда потребный напор равен:
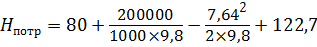
Избыточное давление, необходимое для создания Н потр = 220 м, будет равно:
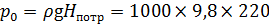
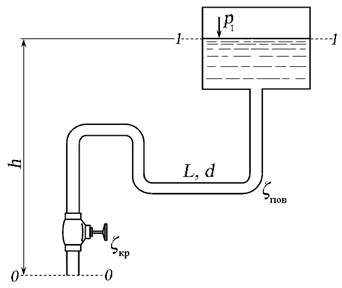
Задача 6.8.4. Определить расход Q в трубе для подачи воды (вязкость ν = 0,01 Ст, плотность ρ = 1000 кг/м 3 ) на высоту h = 16,5 м, если диаметр трубы d = 10 мм, длина L = 20 м, располагаемый напор в сечении 1 — 1 трубы перед краном Н расп = 20 м, коэффициент сопротивления крана ζкр = 4, поворота ζпов = 1. Трубу считать гидравлически гладкой.
Рис. 6.18. Схема к задаче 6.8.4
Уравнение Бернулли для сечений 1 — 1 и 2 — 2 относительно плоскости сравнения — , совпадающей с горизонтальной осью трубы:
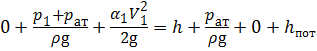

Располагаемый напор Н расп будет равен:
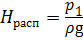
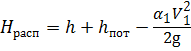
Выразим скорость V 1 через расход Q из уравнения расхода и подставим в скоростной напор 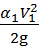
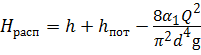
Гидростатический напор в данном случае равен геометрической высоте h ( Н ст = h ). Потери напора
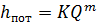
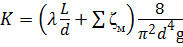


С учётом уравнения для определения располагаемого напора можно записать:
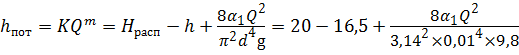
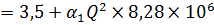
Предположим, что режим движения жидкости — турбулентный ( α = 1, m = 2). Тогда в этом уравнении два неизвестных — Q и λ т, взаимосвязь между которыми определяется зависимостью:
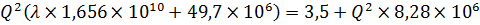
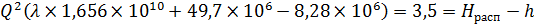
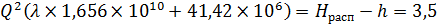
Решим задачу методом последовательных приближений, задаваясь значениями коэффициента λ т ( λ т находится в пределах 0,015 … 0,045). Пусть λ т = 0,03. Тогда, выразив число Рейнольдса Rе из формулы Блазиуса (4.6) для гидравлически гладких труб, получим:
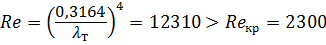
Предположение о турбулентном режиме движении жидкости верно. Определим скорость V 1 и расход Q при Rе = 12310 ( λ т = 0,03):
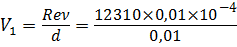
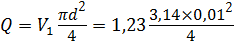
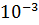
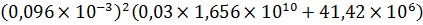
что не соответствует разности 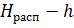
Примем значение λ т = 0,032. Тогда:
Rе = 9509; V 1 = 0,95 м/с; Q = 0,075· 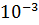
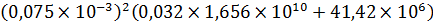
Примем значение λ т = 0,0316. Тогда:
Rе = 10 000; V 1 = 1 м/с; Q = 0,078· 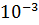
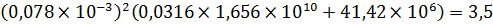
что соответствует 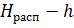
Итак, методом последовательных приближений значение расхода
Q = 0,078· 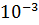
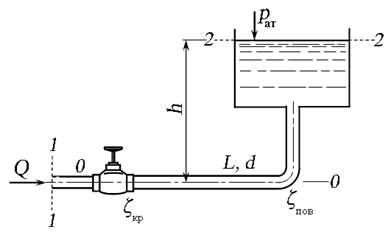
Решим эту же задачу графическим методом. Для этого построим зависимость Н расп = f ( Q ). Выберем ряд значений для расхода Q . Уравнение располагаемого напора представим в виде:
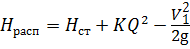
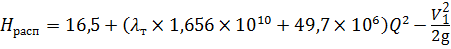
Результаты расчётов сведём в таблицу 4.
Значения параметров для построения графической зависимости Н расп = f ( Q )
Q , 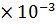 , м 3 /с , м 3 /с | 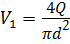 , м/с , м/с |  | 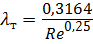 | 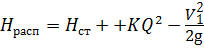 , м , м |
| 0,05 | 0,64 | 0,035 | ||
| 0,07 | 0,89 | 0,0325 | 19,34 | |
| 0,09 | 1,14 | 0,03 | 20,86 | |
| 0,11 | 1,40 | 0,029 | 22,8 | |
| 0,13 | 1,65 | 0,0278 | ||
| 0,15 | 1,91 | 0,0269 | 27,5 |
Рис. 6.19. Графическая зависимость Н расп = f ( Q )
Из построенного графика видно, что при располагаемом напоре Н расп = 20 м расход жидкости составит Q = 0,078 л/с, что соответствует определению расхода методом подбора.
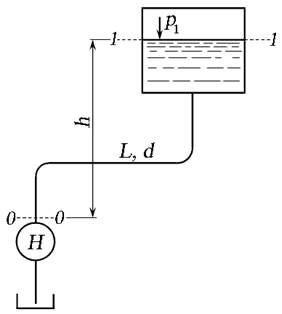
Задача 6.8.5. При каком диаметре трубопровода подача насоса составит Q = 1 л/с, если на выходе из него располагаемый напор Н расп = 9,6 м, длина трубопровода L = 10 м, эквивалентная шероховатость ∆Э = 0,05 мм, избыточное давление в баке р 1 = 30 кПа, высота h = 4 м, вязкость жидкости ν = 0,015 Ст ( 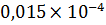
Рис. 6.20. Схема к задаче 6.8.5
Составим уравнение Бернулли для сечений — и 1 — 1 относительно плоскости сравнения, совпадающей с сечением — :
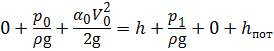
— потери напора 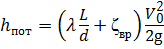
— коэффициент потерь 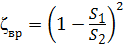
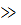
— располагаемый напор 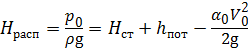
— статический напор 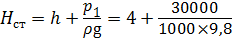
Уравнение Бернулли примет вид:
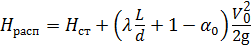
Выразим скорость V 0 течения жидкости через расход Q :
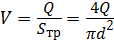
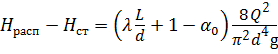
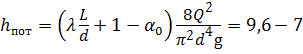
Определим режим течения жидкости. Для этого определим диаметр d трубопровода при Rе = 2300. Воспользовавшись формулой Пуазейля (4.5), сравним получаемую разность напоров с заданной Н расп – Н ст:
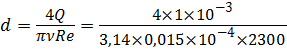
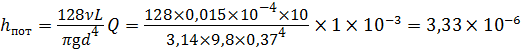
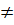
Режим течения, определяемый расходом Q =1 л/с, будет турбулентным ( α = 1). Тогда потери напора определим по формуле:
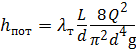
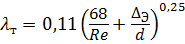
Решим задачу графически. Для этого, задаваясь значениями диаметра d , определим разность напоров Н расп – Н ст по уравнению:

Значения параметров для построения графической зависимости
| d , мм | 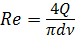 | 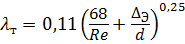 |  |
| 0,03 | 248,1 | ||
| 0,0285 | |||
| 0,0278 | 7,66 | ||
| 0,0276 | 2,36 | ||
| 0,0277 | 0,95 | ||
| 0,028 | 0,45 |
Для более точного построения графика зададим дополнительные значения диаметра d в пределах 21 … 24 мм.
| d , мм | 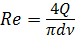 | 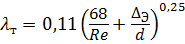 |  |
| 0,0277 | 5,7 | ||
| 0,02772 | 4,4 | ||
| 0,02768 | 3,6 | ||
| 0,02767 | 2,9 |
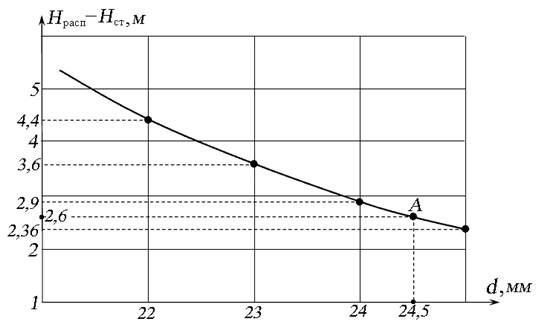
По полученным данным построим график Н расп – Н ст = f ( d ):
Рис. 6.21. График зависимости Н расп – Н ст = f ( d )
При Н расп – Н ст = 2,6 м диаметр трубопровода d = 24,5 мм.
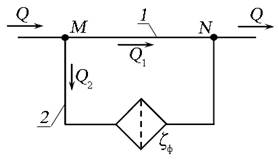
Задача 6.8.6. Трубопровод с расходом жидкости Q = 0,32 л/с в точке М разветвляется на два трубопровода: первый размерами L 1 = 1,0 м и d 1 = 10 мм; второй размерами L 2 = 2,0 м и d 2 = 8 мм. В точке N эти трубопроводы смыкаются. Во втором трубопроводе установлен фильтр, сопротивление которого эквивалентно сопротивлению в трубе длиной L э = 200 d 2. Определить расход и потери давления в каждом трубопроводе, если плотность жидкости ρ = 900 кг/м 3 , кинематическая вязкость ν = 1 Ст. Течение жидкости считать ламинарным.
Рис. 6.22. Схема к задаче 6.8.6
Определим расход Q 1 и Q 2 в каждом трубопроводе по формуле (4.5):
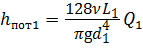
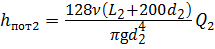
Так как при параллельном соединении трубопроводов потери в них равны ( h пот1 = h пот2), то после сокращения одинаковых величин получим:
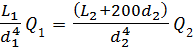
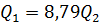
Сумма расхода в точке М в данном случае будет равна сумме расходов в параллельных трубопроводах:
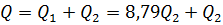
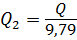
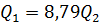
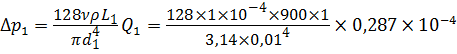
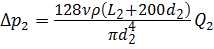
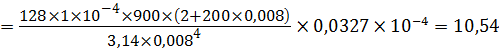
Гидравлическим (пневматическим) приводом называют совокупность гидравлических или пневматических машин, аппаратов и линий, служащих для передачи энергии и преобразование движения выходного звена посредством рабочей среды (жидкости в гидроприводе или воздуха в пневмоприводе).
Источником энергии в пневмоприводе является компрессор, в гидроприводе — насос. Компрессор или насос преобразуют подводимую к ним механическую энергию (например, от электродвигателя или двигателя внутреннего сгорания) в энергию сжатого воздуха или гидравлическую энергию движущейся жидкости.
Потребителем энергии пневмо- или гидропривода являются пневмо- или гидродвигатели, которые преобразуют энергию рабочей среды в механическую энергию.
По назначению различают гидросистемы:
— собственно гидросистемы для создания напора рабочей жидкости (например, система охлаждения и система смазки автомобиля, система топливоподачи, работа стеклоочистителя, автомойка);
— гидропривод для преобразования механической энергии входного звена в механическую энергию выходного звена посредством гидравлической энергии потока рабочей жидкости (например, гидроусилитель руля, тормозная система автомобиля, гидропривод подъёма кузова автомобиля, работа гидротрансформатора АКПП).
Гидравлические системы автомобилей и гаражного оборудования, как и другие гидравлические системы, реализуют свою работу за счёт энергии потока рабочей жидкости. Удельная энергия потока жидкости (энергия единицы веса объёма жидкости) определяется уравнением Бернулли. Передачу энергии за счёт жидкости можно осуществить путём изменения любого из членов этого уравнения:
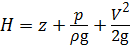
где H — полная удельная энергия потока рабочей жидкости (полный напор);
z — удельная потенциальная энергия положения;
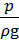
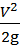
В зависимости от вида используемой в гидромашинах энергии гидравлические системы делят на гидростатические (объёмные) и гидродинамические.
Гидростатический (объёмный) привод. В этом приводе гидромашины в основе своего действия используют потенциальную энергию потока жидкости 

Гидравлический привод, использующий потенциальную и кинетическую энергию движения жидкости 
Использование различных видов энергии объёмным и гидродинамическим приводом объясняется применением различных конструкций гидромашин, а также выполняемых задач. В объёмном гидроприводе используют объёмные гидромашины , а в гидродинамическом – лопастные .
Пневматические компрессоры также в зависимости от вида создаваемой энергии (потенциальной энергии давления или кинетической энергии воздушного потока) различают объёмного или динамического типа. Например, пневмосистемы тормозного привода грузовых автомобилей, привода движения дверей автобуса, являются системами объёмного типа.
Пневматический привод — это устройство для преобразования энергии сжатого воздуха в механическую энергию. Рабочим телом пневмопривода является сжатый воздух — смесь газов.
Процессы сжатия и расширения газов подчиняются законам Бойля — Мариотта и Гей — Люссака.
Пневмосистема — это техническая система, состоящая из механических устройств, которые находятся в контакте со сжатым воздухом. В состав пневмосистем входят:
— блок подготовки сжатого воздуха;
Компрессорная установка включает компрессорный агрегат, состоящий из компрессора с приводом, и дополнительные устройства, обеспечивающие получение сжатого воздуха и размещение его в ресивере с последующим его наполнением в процессе работы пневматического привода.
Блок подготовки сжатого воздуха обеспечивает необходимые условия для работы пневмопривода. К необходимым условиям относят фильтрацию и осушение сжатого воздуха, обеспечение потребителя номинальным давлением, при необходимости увлажнение сжатого воздуха масляным туманом.
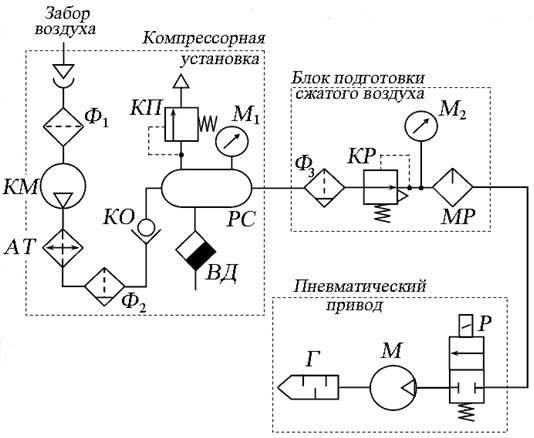
Один из возможных вариантов схемы пневмопривода представлен на рис. 7.1.
Рис. 7.1. Схема пневматической системы (вариант):
Ф 1 — фильтр с воздухозаборником; КМ — компрессор; АТ — аппарат теплообменный (холодильник); Ф 2, Ф 3 — фильтр — влагоотделитель; КО — клапан обратный; РС — ресивер; КП — клапан предохранительный; МН 1, МН 2 — манометр; ВД — влагоотделитель (конденсатоотводчик); КР — клапан редукционный; МР — маслораспылитель; Р — распределитель; М — пневмомотор;
Компрессор КМ , забирая воздух из атмосферы через воздухозаборник с фильтром Ф 1, сжимает его до необходимого давления. При работе компрессора происходит нагрев сжимаемого воздуха до 100 ºС, поэтому после компрессора устанавливают теплообменник (охладитель) АТ , где воздух охлаждается до температуры окружающей сред. Воздух в компрессор поступает загрязнённым. В компрессоре воздух насыщается парами масла. Для очистки и сушки сжатого воздуха на выходе из компрессора служит фильтр — влагоотделитель Ф 2. Ресивер РС служит для запаса сжатого воздуха и сглаживания пульсаций давления, создаваемых при работе компрессора. Предохранительный клапан КП ограничивает величину давления сжатого воздуха в ресивере, периодически спуская воздух из ресивера в атмосферу. Электроконтактный манометр М 1 автоматически отключает работу компрессора при достижении необходимого давления в ресивере, и включает при падении давления ниже заданного значения. Влагоотделитель ВД необходим для слива конденсата, образующегося в ресивере при расширении сжатого воздуха.
Редукционный клапан КР обеспечивает подачу к потребителю сжатого воздуха при постоянном давлении, пониженном (редуцированном) по сравнению с давлением воздуха в ресивере. Манометр М 2 служит для контроля настройки необходимого давления в пневмосети. Так как сжатый воздух имеет очень низкую смазывающую способность, для предотвращения возможного заклинивания подвижных элементов пневматических устройств, а также для смазывания резиновых мембран пневмоаппаратов, на пути сжатого воздуха устанавливают маслораспылитель МР .
При включении распределителя Р сжатый воздух от блока подготовки поступает к потребителю. В изображённом на рис. 7.1 варианте потребителем является пневмомотор М . Глушитель Г необходим для снижения звуковых импульсов на выходе пневмосистемы, причиной которых является турбулизация потока воздух.
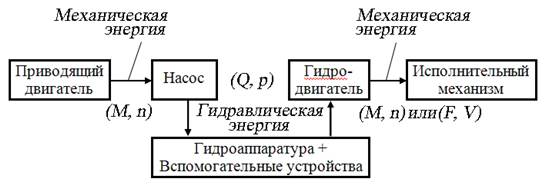
Объёмный гидропривод (ОГП) – это совокупность объёмных гидромашин, гидроаппаратов и вспомогательных устройств, предназначенных для передачи энергии и преобразования движения выходного звена посредством энергии рабочей жидкости. Структурная схема объёмного гидропривода изображена на рис. 7.2.
Рис. 7.2. Структурная схема объёмного гидропривода
Входным звеном гидропривода является вал насоса, выходным – вал гидромотора или шток гидроцилиндра, т. е. это звено гидропривода, совершающее полезную работу. Приводящий двигатель (как правило, электродвигатель или ДВС) преобразует механическую энергию вращения вала в гидравлическую энергию потока рабочей жидкости посредством насоса. Входными параметрами насоса являются вращающий момент М (Н∙м) и частота вращения вала n (об/мин), выходными — расход Q (л/мин) и номинальное давление р (МПа).
В качестве гидродвигателя может использоваться гидромотор, выходными параметрами которого являются вращающий момент М и частота вращения вала n , или гидроцилиндр, выходными параметрами которого являются усилие F (кН) и скорость перемещения штока V (м/мин). Частота вращения вала насоса или вала гидромотора часто обозначается угловой скоростью ω (рад/сек или рад -1 ), связь которой с частотой оборотов n определяется выражением:
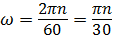
Гидроаппаратура служит для управления и регулирования параметров гидропередачи (давления, расхода, направления движения). К вспомогательным устройствам относят:
— устройства для очистки рабочих жидкостей (фильтры, сепараторы);
— аппараты и приборы для контроля давления (манометры, реле давления и переключатели для них);
— теплообменники (нагреватели и охладители жидкости);
— уплотнения (манжеты, сальники, уплотнительные кольца, прокладки);
— гидролинии (жёсткие и гибкие трубопроводы, каналы);
— аккумуляторы (ёмкости, предназначенные для аккумулирования энергии рабочей жидкости);
— гидробаки (ёмкости, предназначенные для создания запаса рабочей жидкости).
Принцип действия объёмного гидропривода основан на использовании двух главных свойств рабочей жидкости:
— жидкость практически несжимаема;
— она обладает свойством передавать давление по всем направлениям без изменения (закон Паскаля).
Работу объёмного гидропривода рассмотрим на примере простейшей гидропередачи — гидравлического домкрата (рис. 7.3).
Рис. 7.3. Схема гидравлического домкрата:
1 – малый гидроцилиндр (насос); 2 – плунжер; 3 — большой гидроцилиндр (гидродвигатель); 4 – поршень; 5 – рычаг; 6 – напорная гидролиния
В соответствии с законом Паскаля, пренебрегая при этом гидравлическими сопротивлениями, разностью масс плунжера и поршня, а также трением плунжера и поршня в уплотнениях цилиндров, заключаем, что давление в цилиндре 1 и в цилиндре 3 согласно свойствам гидростатики будут одинаковы ( p 1 = p 2 = p ):
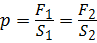
где S 1 и S 2 — рабочая площадь плунжера 2 и поршня 4 соответственно.
Из уравнения (7.2) следует, что 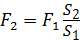
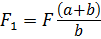
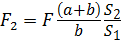
Поскольку жидкость несжимаема, то вытесненные объёмы жидкости W и расход жидкости Q в цилиндрах 1 и 3 на основании уравнения неразрывности потока будут равны между собой:
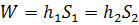
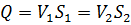
где h 1 и h 2 — перемещение плунжера 2 и поршня 4 в цилиндрах;
V 1 и V 2 — скорость перемещения плунжера 2 и поршня 4 .
Полезная мощность, развиваемая при перемещении плунжера 2 в цилиндре 1 , равна N 1 = F 1 V 1. В идеальном случае (без учёта потерь) она должна быть равна мощности, передаваемой поршню 4 ( N 2 = F 2 V 2), то есть:

Выразим скорость V 1 и V 2 из уравнения расхода (7.4) и подставим её в уравнение (7.5). Тогда мощность данного гидропривода с учётом уравнения (7.2) будет равна:
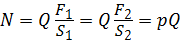
Как видно из уравнения (7.6), полезная мощность гидропривода пропорциональна давлению р и расходу Q рабочей жидкости, то есть увеличение мощности гидропривода можно произвести либо за счёт роста давления р , либо расхода Q .
Увеличение давления за счёт расхода жидкости нерационально, поскольку увеличение расхода Q возможно только за счёт увеличения скорости течения жидкости V (7.4). Рост скорости V течения жидкости ведёт к резкому увеличению потерь давления ∆ р . Потери давления ∆ р = ρ g ∆h определяются разностью пъезометрических высот ∆h , или потерями напора. Потери напора определяются формулой Вейсбаха (4.2), то есть потери давления ∆ р в гидроприводе пропорциональны квадрату скорости, и в конечном итоге – квадрату расхода (в общем случае):
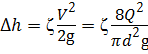
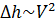
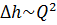
Увеличение мощности объёмного гидропривода осуществляется только за счёт увеличения давления, однако это ведёт к удорожанию всей системы за счёт достаточно сложной конструкции насосов.
В реальности за счёт сил трения в уплотнениях плунжера и поршня, наличия сил вязкости жидкости и инерции подвижных частей гидропривода, загрязнения рабочей жидкости, её нагрева в процессе эксплуатации, утечек жидкости, подводимая мощность на входе N вх и мощность на выходе N вых гидропривода не равны между собой. Их отношение определяет коэффициент полезного действия η гидропривода:
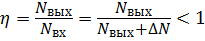
где ∆N — потери мощности в гидроприводе.
Потери мощности гидропривода определяются следующими видами потерь (рис. 7.4):
— объёмные потери или потери расхода ∆Q ;
— гидравлические потери ∆ р ;
— механические потери мощности ∆N м.
Рис. 7.4. Энергетический баланс объёмного гидропривода
Объёмные потери гидропривода ∆Q — это разница между объёмом Q вх поступающей в гидропривод рабочей жидкости и объёмом Q вых на выходе гидропривода:
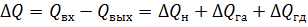
где ∆Q н — объёмные потери в насосе, возникающие вследствие значительной разницы давлений на входе и выходе насоса (часть жидкости через зазоры в элементах конструкции насоса перетекает из напорной линии во всасывающую);
∆Q га — объёмные потери на пути от насоса к гидродвигателю, возникающие вследствие утечек находящейся под давлением рабочей жидкости через уплотнения и зазоры элементов конструкций гидроаппаратов и вспомогательных устройств;
∆Q гд — объёмные перетечки в гидродвигателе, возникающие вследствие значительной разницы давлений на входе и выходе гидродвигателя (часть жидкости через зазоры в элементах конструкции гидродвигателя перетекает из напорной линии в сливную).
Объёмные потери гидропривода оценивают объёмным КПД:
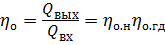
где η о.н — объёмный КПД насоса;
η о.гд — объёмный КПД гидродвигателя.
Объёмные потери ∆Q га при расчёте гидропривода не учитывают, поскольку при качественной сборке элементов конструкций гидропривода, соединении гидролиний и надлежащем техобслуживании эти потери практически равны нулю. При необходимости долю внешних утечек учитывают с помощью коэффициента k , который всегда меньше единицы.
Гидравлические потери ∆ р — это потери давления в гидросети, которые обусловлены гидравлическими потерями в трубопроводах и каналах гидропривода и определяются в соответствии с законами гидравлики. Потери давления ∆ р характеризуются гидравлическим КПД:
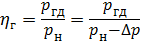
где р н — давление на выходе из насоса;
р гд — давление на входе в гидродвигатель.
Механические потери мощности ∆N м — это потери, связанные с механическим трением конструктивных элементов гидромашин (например, потери, обусловленные трением вала в подшипнике скольжения или в уплотнениях поршня гидроцилиндра). Механические потери проявляются в снижении силовых параметров гидропривода и определяются механическим КПД:
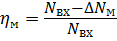
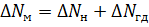
где ∆Nн — механические потери мощности в насосе;
∆Nгд — механические потери мощности в гидродвигателе.
Полный КПД гидропривода — это произведение объёмного η о, гидравлического η г и механического η м КПД. На практике гидравлический и механический КПД объединяют в одно значение гидромеханического η гм КПД. Тогда полный КПД гидропривода:
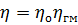
В объёмном гидроприводе используют объёмные гидромашины, которые по характеру движения вытеснителя рабочей жидкости подразделяются на машины поступательного движения вытеснителя, вращательного и вращательно — поступательного. Гидромашины поступательного движения вытеснителя относят к поршневым насосам и гидроцилиндрам, вращательного действия — к роторным насосам и гидромоторам.
В объёмной гидромашине рабочая жидкость перемещается за счёт периодического изменения объёма занимаемой ею камеры, попеременно сообщающейся с входом и выходом гидромашины.
Гидродинамическими (ГПД) называются передачи, в которых главной составляющей энергии потока жидкости является кинетическая энергия. Главным элементом передачи является лопастной насос (рис. 7.5), в котором рабочим органом является лопастное колесо 2 , на котором установлены профильные лопатки 5 . Жидкость движется от подвода 1 насоса к отводу 4 в форме диффузора 3 со спиральной осью.
Рис. 7.5. Центробежный насос:
а ) — принципиальная схема; б ) — условное изображение;
1 — подвод; 2 — лопастное колесо; 3 — диффузор; 4 — отвод
Особенностью лопастных насосов является тот факт, что вход и выход насоса не разделены, и вращение рабочего колеса происходит в неразделённом потоке жидкости. Поэтому насосы являются несамовсасывающими, и перед пуском должны быть заполнены жидкостью.
Параметры лопастных насосов, характеризующие их работу, делят на внешние и внутренние. К внешним параметрам относят:
— частота вращения вала насоса n , об/мин;
— крутящий момент на валу M , Нм;
— мощность на валу насоса 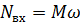
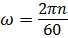
К внутренним параметрам относят:
— расход или подача Q , м 3 /с;
Напор насоса Н — это энергия, сообщаемая насосом единице веса жидкости, то есть это разность удельных энергий, которой обладает жидкость между входом и выходом насоса:
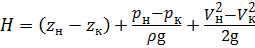
где индекс н — сечение на выходе колеса;
индекс к — сечение на входе колеса.
Мощность потока жидкости на выходе насоса:

Коэффициент полезного действия насоса:
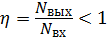
Потери мощности 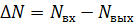
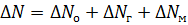
Объёмные потери мощности ∆ N о определяются перетечками жидкости из напорной линии во всасывающую через зазоры, образованные рабочим колесом и внутренней поверхностью лопастного насоса. Гидравлические потери ∆ N г — это потери на трение в подводе, отводе насоса и каналах рабочего колеса. Механические потери ∆ N м определяются потерями на трение в подшипниках и в уплотнениях вала насоса. Эти потери составляют значительную часть подводимой мощности:
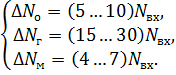
Для преобразования гидравлической энергии потока жидкости, направляемого от лопастного насоса, в механическую энергию вращения выходного вала, применяют гидротурбины . Структурная схема гидродинамической передачи (ГДП), включающая лопастной насос и гидротурбину, изображена на рис. 7.6.
Рис. 7.6. Принципиальная схема гидродинамической передачи:
1 — насосное колесо; 2 — турбинное колесо
Гидродинамические передачи состоят из расположенных соосно и максимально сближенных в общем корпусе рабочих органов лопастного насоса и гидравлической турбины — насосного и турбинного колеса. В насосе механическая энергия с параметрами M н и n н преобразуется в поток жидкости с параметрами Q н и H н. На турбинном колесе энергия этого потока преобразуется в механическую энергию M т и n т. На выходе из турбинного колеса поток жидкости с параметрами Q т и H т, проходя через реакторное колесо, снова попадает на вход насосного колеса.
Реакторное колесо необходимо для преобразования параметров гидравлической энергии с целью получения определённых характеристик гидродинамической передачи — крутящего момента M т и частоты вращения n т.
Основываясь на принципиальной схеме гидропередачи с помощью центробежного насоса и гидротурбины (рис. 7.7, а ), немецкий учёный и инженер Г. Феттингер в 1902 году предложил устранить соединительный трубопровод 2 , а насос 1 , турбину 4 и направляющий элемент 3 (реактор) объединить в одном корпусе.
Рис. 7.7. Схема гидродинамической передачи:
а ) — гидропередача с помощью центробежного насоса и гидротурбины;
б ) — принципиальная схема гидротрансформатора;
1 — лопастной насос центробежного типа; 2 — соединительный трубопровод; 3 — направляющий элемент (реактор); 4 — гидротурбина; 5 — сливной патрубок; 6 — всасывающий патрубок; 7 — гидробак; ПД — приводной двигатель
В таком устройстве рабочая жидкость, проходя последовательно через насосное колесо, реактор и турбинное колесо, обеспечивает не только передачу крутящего момента от вала насоса к валу турбины, но и его изменение. Изменение крутящего момента обусловлено тем, что жидкость, проходя через неподвижный реактор, изменяет момент количества движения, и соответственно, передаваемый крутящий момент. Такой гидроаппарат был назван гидродинамическим трансформатором (ГДТ). Уравнение моментов гидротрансформатора в общем случае:
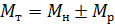
Для повышения экономичности из гидротрансформатора был изъят реактор. Так появилась новая гидродинамическая передача, которая получила название гидродинамической муфты (ГДМ). Гидромуфта передаёт крутящий момент от насосного колеса к турбинному без изменения крутящего момента:

Теория операции
Основная трубка Пито состоит из трубки, направленной прямо в поток жидкости. Поскольку в этой трубке находится жидкость, можно измерить давление; движущаяся жидкость останавливается (застаивается), поскольку нет выхода для продолжения потока. Это давление представляет собой давление застоя жидкости, также известное как полное давление или (особенно в авиации) давление Пито .
Измеренное давление торможения само по себе не может использоваться для определения скорости потока жидкости (воздушной скорости в авиации). Однако уравнение Бернулли гласит:
Давление застоя = статическое давление динамическое давление
Что тоже можно написать
птзнак равнопs (ρты22). < displaystyle p_left (< frac < rho u ^ <2>> <2>> right) ,.>
Решение этого для скорости потока дает
тызнак равно2(пт-пs)ρ, < displaystyle u = < sqrt < frac <2 (p_)> < rho>>> ,,>
ПРИМЕЧАНИЕ. Приведенное выше уравнение применимо только к жидкостям, которые можно рассматривать как несжимаемые. Жидкости считаются несжимаемыми почти во всех условиях. Газы при определенных условиях можно считать несжимаемыми. См. Сжимаемость .
Таким образом, динамическое давление — это разница между давлением торможения и статическим давлением. Затем динамическое давление определяется с помощью диафрагмы внутри закрытого контейнера. Если воздух с одной стороны диафрагмы находится под статическим давлением, а с другой — с давлением торможения, то прогиб диафрагмы пропорционален динамическому давлению.
В самолетах статическое давление обычно измеряется с помощью статических отверстий на боковой стороне фюзеляжа. Измеренное динамическое давление можно использовать для определения указанной воздушной скорости самолета. Описанное выше устройство диафрагмы обычно содержится в индикаторе воздушной скорости , который преобразует динамическое давление в показания воздушной скорости с помощью механических рычагов.
Вместо отдельных портов Пито и статических отверстий можно использовать статическую трубку Пито (также называемую трубкой Прандтля ), которая имеет вторую трубку, коаксиальную с трубкой Пито, с отверстиями по бокам, за пределами прямого воздушного потока, для измерения статического давления. .
Если манометр столба жидкости используется для измерения перепада давления ,
Δп≡пт-пs < displaystyle Delta p Equiv p_>
Δчасзнак равноΔпρлграмм, < displaystyle Delta h = < frac < Delta p> < rho _
тызнак равно2Δчасρлграммρ. < displaystyle u = < sqrt < frac <2 , Delta h , rho _
Некоторые практические приложения уравнения Бернулли
Рассмотрим применение уравнения Бернулли для определения скоростей и расходов и времени истечения жидкостей из резервуаров.
Принципы измерения скорости и расхода жидкости. Для определения скоростей и расходов жидкостей в промышленной практике обычно применяются дроссельные приборы и пневмометрические трубки.
Принцип работы пневмометрических трубок, например трубки Пито-Прандтля, может быть пояснен с помощью рис. II-16. В каждом сечении разность уровней жидкости в трубках, изображенных на рисунке, выражает скоростной напор hск в точке сечения, лежащей на оси трубы.
Разность уровней рабочей жидкости в трубках удобнее измерять не посредством пьезометрических трубок, как показано на рис. II-16, а при помощи дифференциального манометра (рис. II-17). Его U-образная трубка заполнена жидкостью, которая не смешивается с рабочей и имеет значительно большую плотность, чем последняя (например, вода или спирт – при работе с газами или ртуть – при работе с капельными жидкостями). Это позволяет измерять перепады давлений в случае значительного избыточного давления (или вакуума) в трубопроводе при относительно небольшой высоте прибора.
По результатам измерений 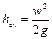
Такой способ определения скорости и расхода жидкости прост, но недостаточно точен из-за трудности установки пневмометрических трубок строго вдоль оси трубопровода.

В качестве дроссельных приборов используют мерные диафрагмы, сопла и трубы Вентури.
Мерная диафрагма (рис. II-17) представляет собой тонкий диск с отверстием круглого сечения, центр которого расположен на оси трубы. Мерное сопло (рис. II-18) является насадкой, имеющим плавно закругленный вход и цилиндрический выход. Дифманометры мерных сопел (а также диафрагм) присоединяют к трубопроводу через кольцевые камеры а, соединенные с внутренним пространством трубопровода отверстиями, равномерно расположенными по окружности, или двумя каналами b.




В трубе Вентури и в сопле площадь сечения сжатой струи S2 = 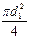
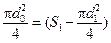
Коэффициент a называется коэффициентом расхода дроссельного прибора. Его значение зависит от значения критерия Рейнольдса для жидкости и от отношения диаметра отверстия дроссельного прибора к диаметру трубопровода:
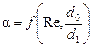
Значения a, определенные опытным путем, приводятся в специальной и справочной литературе.
Диаметр дроссельного устройства обычно в 3-4 раза меньше диаметра трубопровода, поэтому величиной (d2/d1) 2 в уравнении (II,54) можно в первом приближении пренебречь и находить расход жидкости по уравнению
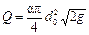
Среднюю скорость жидкости в трубопроводе определяют, разделив Q на площадь сечения трубопровода. Опуская индексы «1» у w1 и d1, получим
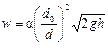
В случае работы со сжимаемыми жидкостями (газом или паром) при больших перепадах давлений в уравнения (II,56) и (II,57) вводят еще один поправочный коэффициент, учитывающий изменение плотности газа (пара).
Истечение жидкостей. Определим расход жидкости при ее истечении через круглое отверстие в тонком днище открытого сосуда, в котором поддерживается постоянный уровень H жидкости (рис. II-20, а).
Вытекающая из такого отверстия струя резко сжимается при выходе вследствие инерционного движения частиц жидкости, приближающихся внутри сосуда к отверстию по криволинейным траекториям (некоторые из них даже непосредственно перед выходом еще скользят почти параллельно днищу, то есть перпендикулярно оси струи). Расстояние от днища до сжатого сечения (вслед за которым дальнейшее сужение струи из-за увеличения скорости падающей жидкости выражено гораздо слабее) невелико и составляет около половины диаметра отверстия.
Выбрав плоскость сравнения 0—0 параллельной днищу сосуда, напишем уравнение Бернулли (считая жидкость идеальной) для сечения 1—1, соответствующего верхнему уровню жидкости в сосуде, и сечения 2—2, плоскость которого проходит через указанное сжатое сечение вытекающей струи:
Для открытого сосуда р1 = р2; кроме того, при постоянном уровне жидкости скорость ее w1 = 0. Пренебрегая небольшим расстоянием от плоскости отверстия в днище сосуда до плоскости сжатого сечения струи, можно принять, что zl — z2 » H. Отсюда
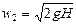
что соответствует известной формуле Торричелли.
При движении реальной жидкости часть напора H теряется на трение и преодоление сопротивления, обусловленного внезапным сужением потока в отверстии. Поэтому скорость реальной жидкости в сжатом сечении:
где j — поправочный коэффициент (j 3 /сек) жидкости равен произведению ее скорости w2 на площадь сжатого сечения S2 струи. Обозначим отношение S2 площади поперечного сечения S0 отверстия в днище через e. Это отношение e = S2/S0 называют коэффициентом сжатия струи.
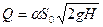
Коэффициент a представляет собой коэффициент расхода и выражается произведением коэффициентов скорости и сжатия струи:
Этот коэффициент определяют опытным путем, его значения зависят от значения критерия Re и могут быть найдены в справочниках в зависимости от свойств и скорости жидкости, а также от формы отверстия, его размера и удаленности от стенок сосуда.
Из уравнения (II,59) следует, что расход жидкости, вытекающей через отверстие в тонком днище, зависит от высоты постоянного уровня жидкости над отверстием и от размера отверстия, но не зависит от формы сосуда. Это уравнение применимо также для определения расхода жидкости, вытекающей через отверстие в тонкой боковой стенке сосуда, если считать Н расстоянием от верхнего уровня жидкости до оси отверстия.
Для жидкостей, по вязкости мало отличающихся от воды, можно принимать в первом приближении ее a » 0.62. При истечении жидкости через короткий цилиндрический патрубок (насадок) происходит дополнительная потеря напора на входе и выходе жидкости, что приводит к снижению j. Вместе с тем струя при входе в патрубок после некоторого сжатия снова расширяется и вытекает, заполняя все его сечение, т.е. можно считать e = I. В итоге коэффициент расхода жидкости при истечении через насадок оказывается большим, чем при истечении через отверстие, и для воды может быть принят a » 0.82.
Если сосуд, из которого вытекает жидкость, закрыт и давление р2 над жидкостью в нем отличается от наружного давления р1, то при определении расхода по формуле (II,59) вместо H в нее следует подставить 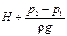
Теперь рассмотрим истечение при переменном уровне жидкости в сосуде с целью определения времени опорожнения сосудов.
При таком истечении жидкости (рис. II-20,б) ее уровень H в сосуде снижается во времени и, согласно уравнению (II,58), уменьшается также скорость истечения w0. Следовательно, процесс истечения носит нестационарный характер.
Определим время, за которое уровень жидкости в сосуде опустится от первоначальной высоты H1 до некоторой высоты H2. За бесконечно малый промежуток времени dt., в соответствии с уравнением (II,59), через отверстие в днище вытечет объем жидкости
dV = Qdt = aS0
где S0 — площадь поперечного сечения отверстия в днище сосуда.
За тот же промежуток времени dt уровень жидкости в сосуде понизится на бесконечно малую величину dH, и при постоянной площади поперечного сечения S сосуда убыль жидкости в нем составит
Знак минус в правой части указывает на уменьшение высоты жидкости в сосуде.
Приравнивая, согласно уравнению неразрывности потока, эти объемы, получим
aS0 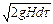
Проинтегрируем это выражение, принимая, что коэффициент расхода a постоянен, т.е. не зависит от скорости истечения:
Таким образом, время опорожнения сосуда, имеющего постоянно поперечное сечение, от высоты H1 до высоты H2 составляет
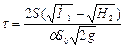
В случае полного опорожнения резервуара H2 = 0 и уравнение (II,61) принимает вид
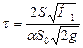
Решая задачу о времени опорожнения сосуда, площадь поперечного сечения которого изменяется по высоте (например, при истечении из конических резервуаров, горизонтальных цистерн и т.п.), следует при интегрировании выражения dt. учесть зависимость площади сечения S от уровня Н жидкости, т.е. учесть вид функции S = f(H).
Основы гидравлики
Уравнение Бернулли — фундамент гидродинамики
Бернулли — вне всякого сомнения — имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.
Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.
Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S1 и S2 , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S1 скорость течения ν1 , давление p1 и высота, на которой это сечение расположено, h1 . Аналогично, в месте сечения S2 скорость течения ν2 , давление p2 и высота сечения h2 .
За бесконечно малый отрезок времени Δt жидкость переместится от сечения S1 к сечению S1‘ , от S2 к S2‘ .
По закону сохранения энергии, изменение полной энергии E2 — E1 идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:
где E1 и E2 — полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.
С другой стороны, А — это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S1 и S2 , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S1 до S1‘ жидкость должна переместиться на расстояние L1 = ν1Δt и от S2 до S2‘ — на расстояние L2 = ν2Δt . Отметим, что L1 и L2 настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,
где F1 = p1S1 и F2 = — p2S2 (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).
Полные энергии E1 и E2 будут складываться из кинетической и потенциальной энергий массы m жидкости:
Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим
Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.
Разделив выражение (5) на ΔV , получим
где ρ — плотность жидкости.
После некоторых преобразований эту формулу можно представить в другом виде:
Поскольку сечения выбирались произвольно, то в общем случае можно записать:
ρv 2 /2 +ρgh +p = const (6) .
Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.
Даниил Бернулли (Daniel Bernoulli, 1700 — 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).
Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.
Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 — динамическим давлением, величина ρgh — гидростатическим давлением.
Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением — давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.
Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:
ρv 2 /2 + p = const (7) .
Выражение p + ρν 2 /2 называется полным давлением.
Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.
Все члены уравнения Бернулли измеряются в линейных единицах.
В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину hп = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.
Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора — полным напором.
На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.
Геометрическая интерпретация уравнения Бернулли
Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.
На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .

Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’e (удельной механической энергии) идеальной струйки в любом ее сечении.
При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить hf потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:
Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.
Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:
Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.
Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:
где α1 , α2 — коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α1 = α2 = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.
Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S1v1Δt = S2v2Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.
Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.
Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .
Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая — прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:
Определив с помощью трубки Пито — Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:
Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.
Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h1 выхода ее из отверстия) и применим уравнение Бернулли:
Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р1 = р2 , то уравнение будет иметь вид
Из уравнения неразрывности мы знаем, что ν1/ν2 = S2/S1 , где S1 и S2 — площади поперечных сечений сосуда и отверстия.
Если S1 значительно превышает S2 , то слагаемым ν1 2 /2 можно пренебречь и тогда:
Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.
Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .
Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .
Пример решения задачи на определение расхода жидкости
Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие — µs = 0,62.
По формуле Торричелли определим скорость истечения воды из отверстия:
v = √2gh = √2×10×1 ≈ 4,5 м/с.
Определим расход воды Q за время t = 10 секунд:
Q = µsvSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.
На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.
При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .
http://helpiks.org/7-10102.html
http://k-a-t.ru/gidravlika/7_Bernulli/