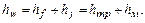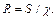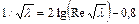Уравнение Бернулли для струйки вязкой несжимаемой жидкости.




Уравнение Бернулли для струйки вязкой несжимаемой жидкости.
Он справился со многими проблемами в динамике жидкостей и газов. gases. In в частности, он получил уравнения, описанные для случая стационарного движения несжимаемых жидкостей. **Здесь мы используем метод получения уравнения Бернулли, который описан в скалярной версии[15], в векторной форме. Людмила Фирмаль
- Представляет производную функции e в направлении 5.И так оно и есть.、 (5.19)) −01 ′ е + вчп-аз == Если мы интегрируем это уравнение вдоль линий тока от раздела 1 до раздела 2 в данный момент, мы получим: Например-Ei + V \ / yes, (5.20) * 1 А =и Где индексы 1 и 2 это значения разделов 1 и 2. Если только гравитация работает из массовой силы, то Φ= dg, и если мы введем обозначение、 *• В разрезе элемента текущей трубы, предполагая, что параметры потока не изменяются, уравнение (5.23) справедливо вдоль трубы, а ее ось можно рассматривать как выбранную линию потока. Восемьдесят семь Локальное ускорение везде*, уравнение (5.23) имеет вид Для стационарного движения есть zero. In этот случай| =просмотр D. это уравнение, называемое уравнением Бернулли, является одним из 1 основных уравнений механики жидкости.
- Определите его физический смысл. <Ди! Д1 ″ 0)] Сначала рассмотрим стационарное движение и перепишем формулу (5.19) в виде: = −4, » + УФИ-ае. (5.19 ’) ГБ На левой стороне находится производная направления-5 от величины и2 / 2, называемая плотностью кинетической энергии. По существу, u2 / 2-это кинетическая энергия жидкой частицы и относится к единице ее массы. Величина-8F является производной потенциала массовой силы и, как известно из общей механики, является фундаментальной работой этой силы. чтобы интерпретировать значение c18p / (p@)$, рассмотрим живое поперечное сечение основной токовой трубки, где скорость жидкости равна и давление равно p (рис.5.3). За время n1, если частицы в этом сечении переместились только на расстояние u. давление работы pu8 вдоль этого пути будет равно pu8isI. Если перевести эту работу в массу жидкости объема s8uI, то величина p / p есть работа давления на единицу массы.
Последний член уравнения (5.19′) является работой удельной (то есть называемой единичной массой) вязкой силы g2D на основном пути. Отметим, что в данном разделе учитывается работа вязких напряжений, как внутренних, так и внешних. Людмила Фирмаль
- Таким образом, уравнение (5.19′) представляет собой теорему биомеханики для бесконечно малых объемов жидкости из разности удельной кинетической энергии и равно сумме фундаментальной удельной работы всех внутренних и внешних масс и поверхностных сил, действующих на определенный объем жидкости. Теорема биомеханизма, полученная из уравнения движения, выражает баланс механической энергии и является частным случаем закона сохранения энергии в случае идеальной жидкости (V = 0). Переходя к конечному виду уравнения[ссылка(5.24) 1, представим его в следующем виде = Р, Р2 + Р-> К (5.24 ’) Здесь все термины присваиваются единицам веса и имеют линейные размеры.
Из Формулы (5.24′) видно, что изменение конкретной кинетической энергии равно сумме удельной работы силы тяжести Восемьдесят восемь (2X-r2), давление (pg-p ^ 1 (pb) и вязкость (K), то есть это уравнение представляет теорему жизнеспособности в конечной форме. В случае общего нестационарного движения получено уравнение(5.23), а член K\%, называемый давлением инерции, равен entered. As как видно из Формулы (5.22), она зависит от локального ускорения d / q1 и, как показано, представляет собой обратимое преобразование энергии, присущее нестационарному движению. Об этом, ч. 6.
Смотрите также:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Уравнение Бернулли
Уравнение Бернулли для струйки жидкости формулируется следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Уравнение Бернулли выглядит так:
Подробное описание всех входящих в состав уравнения параметров уже описан в этой статье.
Содержание статьи
Смысл уравнения Бернулли
По существу вывода уравнение Бернулли для струйки идеальной жидкости представляет собой закон сохранения механической энергии, составленный применительно к единице массового расхода жидкости. Это следует из того, что в процессе вывода значения работы сил, приложенных к выделенному объему струйки и значения кинетической энергии этого объема были поделены на величину ρqΔT.
Отсюда вытекает, что поскольку член υ 2 /2 является мерой кинетической энергии единицы массы движущейся жидкости, то сумма членов gz+p/ρ будет мерилом ее потенциальной энергии.
В отношении величины gz это очевидно, ведь если частица жидкости массы m расположена на высоте z относительно некоторой плоскости и находится под действием сил тяжести, то способность ее совершить работу, т.е. её потенциальная энергия относительно этой плоскости равняется mgz. Но если её поделить на массу частиц m, то эта часть потенциальной энергии даст величину gz.
Для более ясного физического представления о том, что потенциальная энергия измеряется величиной p/ρ рассмотрим такую схему: пусть к трубе, заполненной жидкостью с избыточным давлением p, присоединен пьезометр, снабженный на входе в него краном.
Кран сначала закрыт, т.е. пьезометр свободен от жидкости, а элементарный объем жидкости ΔV массой ρ*ΔV перед краном находится под давлением p.
Если затем открыть кран, то жидкость в пьезометре поднимется на некоторую высоту, равную
Таким образом, единица массы, находящейся под давлением p, как бы несет в себе ещё заряд потенциальной энергии, определяемой величиной p/ρ.
В гидравлике для характеристики удельной энергии обычно используется понятие напор, под которым понимают энергию жидкости, отнесенную к единице силы тяжести, а не её массы. В соответствии с этим уравнение Бернулли записанное в начале этой статьи примет вид
Такое уравнение Бернулли для элементарной струйки идеальной жидкости в другой форме, весьма удобно для гидравлических расчетов и может быть сформулировано следующим образом.
Для элементарной струйки идеальной жидкости полный напор, т.е. сумма геометрического, пьезометрического и скоростного напоров, есть величина постоянная во всех её сечениях.
Отсюда следует, что между напором и удельной энергией существует очень простая зависимость
где э – удельная энергия
Уравнение Бернулли для элементарной струйки реальной жидкости
Если вместо идеальной жидкости рассматривать жидкость реальную, то уравнение Бернулли для реальной жидкости должно принять несколько другой вид.
При движении идеальной жидкости её полная удельная энергия или напор сохраняет постоянное значение по длине струйки, а при движении реальной жидкости эта энергия будет убывать по направлению движения. Причиной этого являются затраты энергии на преодоление сопротивлений движению, обусловленные внутренним трением в вязкой жидкости.
Если же мы рассмотрим два сечения для струйки идеальной жидкости: 1-1 в начале и 2-2 в конце струйки, то полная удельная энергия будет
Полная удельная энергия для сечения 1-1 всегда будет больше, чем полная удельная энергия для сечения 2-2 на некоторую величину потерь, и уравнение Бернулли в этом случае получается
Величина Э1-2 представляет собой меру энергии, потерянную единицей массы жидкости на преодоление сопротивлений при её движениями между указанными сечениями.
Соответствующий этой потере удельной энергии напор называют потерей напора между сечениями 1-1 и 2-2 и обозначают h1-2 . Поэтому уравнение Бернулли для элементарной струйки реальной жидкости можно представить в виде
Уравнение Бернулли для потока реальной жидкости
Уравнение Бернулли для струйки реальной жидкости это еще только половина дела, ведь в при решении различных практических вопросов о движении жидкостей приходится иметь дело с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено, исходя из рассмотрения потока как совокупности множества элементарных струек.
Учитывая, что все струйки движутся с одной и той же средней скоростью форма записи уравнения Бернулли для потока идеальной жидкости становится идентичной его записи для элементарной струйки.
В таком виде уравнение Бернулли обычно и применяется при решении практических задач для потоков однородной несжимаемой жидкости при установившемся движении, происходящем под действием одной силы тяжести.
Такое уравнение составляется для различных живых сечений потока, вблизи которых движение жидкости должно удовлетворять условиям медленно изменяющегося движения, хотя на пути между этими сечениями движение может и не удовлетворять указанным условиям.
Слагаемое h1-2 в этом уравнении показывает потери напора на преодоление сопротивлений движению жидкости. При этом в гидравлике различают два основных вида сопротивлений:
— hлп — линейные потери — сопротивления, проявляющиеся по всей длине потока, обусловленные силами трения частиц жидкости друг о друга и о стенки, ограничивающие поток.
— hмп — местные потери – местные сопротивления, обусловленные различного рода препятствиями, устанавливаемыми в потоке (задвижка, кран, колено), приводящими к изменениям величины или направления скорости течения жидкости
Поэтому полная потеря напора между двумя сечениями потока при наличии сопротивлений обоих видов будет
Видео по теме
Уравнение Бернулли подходит и для газов. Явление уменьшения давления при повышении скорости потока является основой работы различных приборов для измерения расхода. Закон Бернулли справедлив и для жидкостей вязкость которых равна нулю. При описании течения таких жидкостей используют уравнение Бернулли с добавлением слагаемых учитывающих потери на местные сопротивления.
Уравнение Бернулли для потока несжимаемой жидкости
К одномерным относятся течения, описываемые одной координатой. Для установившихся течений одномерное уравнение Бернулли для потока конечных размеров имеет вид
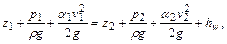
где 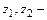
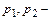
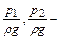
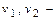
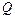
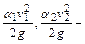
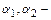
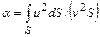
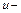
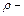
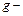
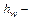
При ламинарном течении в круглых трубах 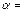
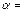
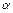
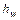
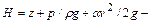
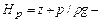
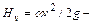
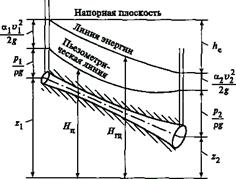
Рис.8.1. Геометрическая интерпретация уравнения Бернулли
для потока несжимаемой жидкости
Основной причиной потерь энергии 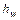
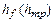
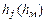
Потери по длине
Потери по длине возникают при течении жидкостей и газов по цилиндрическим трубам или каналам с постоянной по длине потока средней скоростью. В этих случаях потери напора определяются по формуле Дарси — Вейсбаха
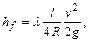
где 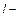
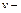
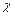
Для круглых труб 4R=d , где d — диаметр трубы и формула приобретает вид
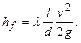
Потери энергии, выраженные в размерности давления, определяются по формуле
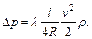
Гидравлический коэффициент трения 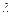
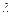
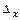
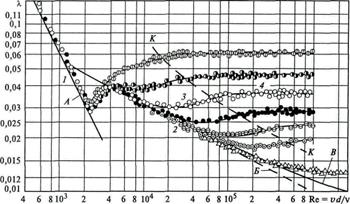
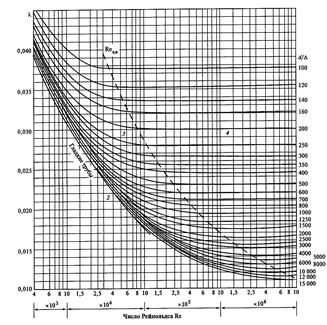
Рис.8.2. Зависимость гидравлического коэффициента трения от числа Рейнольдса
для круглых труб с однородной шероховатостью:
1-2 — зоны ламинарного и гладкостенного режимов; 3-4 — зоны доквадратичного и квадратичного сопротивлений; К-К — нижняя граница квадратичного режима; А — расчет по формуле 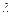
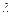
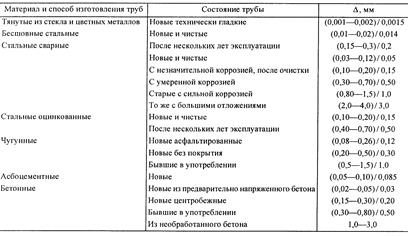
Эквивалентная абсолютная шероховатость труб из разных материалов
Примечание. В числителе приведены пределы изменения 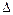
Для промышленных труб, в которых шероховатость неравномерна, в качестве ее характеристики применяется эквивалентная абсолютная шероховатость 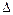
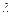
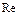
Наиболее распространенные зависимости для коэффициента 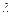
Сжимаемость газов мало влияет на зависимость 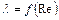
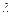
Внутренняя структура течения в круглых трубах зависит от режимов течения.
Рис.8.3. Расчетный график гидравлического коэффициента трения
для стальных круглых труб с естественной шероховатостью, по данным ВТИ:
2-4 — зоны соответственно гладкостенного, доквадратичного и квадратичного режима;
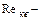
При стабилизированном ламинарном течении распределение местных скоростей подчиняется параболическому закону
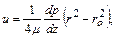
или в безразмерном виде
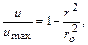
где р — давление; 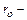
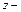
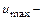
Расчетные формулы для гидравлического коэффициента трения
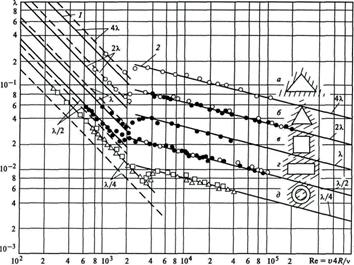
Рис.8.4. Зависимость гидравлического коэффициента трения
от числа Рейнольдса для труб некруглого сечения:
1 — ламинарное течение, 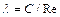
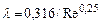
_ _ — ламинарное течение в круглой трубе, 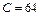
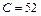
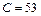
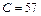
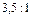
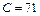
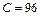
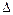
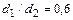
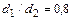
Средняя скорость в 2 раза меньше максимальной: 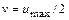
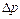
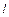
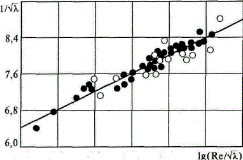
Рис.8.5. Зависимость гидравлического коэффициента трения
для гладкой трубы от числа Рейнольдса:
расчет по формуле Прандтля – Никурадзе
Из уравнения Бернулли, составленного для граничных сечений участка 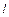
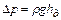
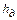
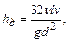
откуда вытекает, что 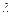
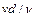
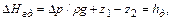
где 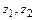
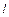
Стабилизированное течение устанавливается лишь на некотором расстоянии от входа в трубу, за пределами начального участка, длина которого для круглой трубы 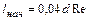
Падение давления на начальном участке не подчиняется формуле Пуазейля, но приближенно может быть определено по формуле
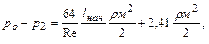
где 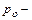
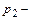
Разрушение ламинарного режима в трубе и переход к турбулентному режиму происходит при достижении критического числа Рейнольдса. Для круглых труб это значение составляет приблизительно 2300. При 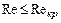
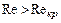
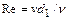
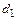
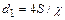
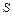
При стабилизированном турбулентном течении в трубах распределение местных осредненных скоростей описывается полуэмпирическими или эмпирическими формулами. Наиболее известные из них:
логарифмическая формула для гладкостенного режима течения
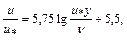
где 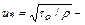
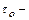
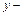
Другая форма этой зависимости имеет вид
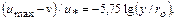
где 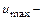
Средняя скорость связана с максимальной соотношением
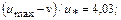
универсальная логарифмическая формула для всех турбулентных режимов в шероховатых трубах
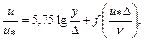
где функция 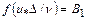
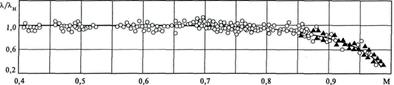
Рис.8.6. Влияние числа Маха на гидравлический коэффициент трения
при дозвуковом течении газа в гладкой трубе:
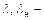
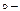
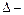
степенная формула (эмпирическая)
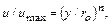
где показатель 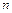
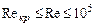
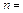
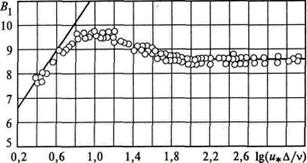
Рис.8.7. Вид функции 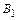
в шероховатых трубах
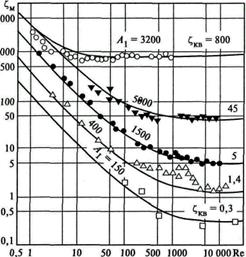
Рис. 8.8. Зависимость коэффициента местных сопротивлений от числа Рейнольдса:
— тройник; Ñ — шаровой клапан; 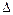
Дата добавления: 2016-02-16 ; просмотров: 2224 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
http://www.nektonnasos.ru/article/gidravlika/uravnenie-bernulli/
http://helpiks.org/7-7289.html