Уравнение бернулли и формула пуазейля

Основы гемодинамики

Поделитесь этим или сохраните на стену

Это серия видео, плейлист из 7 коротких видео, каждое из которых посвящено отдельному вопросу физики тока крови. Эти вопросы — самые элементарные для начинающих изучать гемодинамику. Видео записаны мной в самом начале 2019 года. У меня есть мечта — вернуться к этой теме и записать это более качественно и доступно, чтобы не приходилось останавливать и вникать в формулы. Но какое-то время я намерен плотно заниматься работой для клиницистов. Возможно, всё ещё впереди.

Содержание плей-листа

1. Формула Пуазёйля

Формула пуазёйля — это уравнение, выражающее прямую пропорциональность перепада давления вдоль трубки её длине, скорости потока через трубку, вязкости жидкости, и обратную пропорциональность этого перепада четвертой степени внутреннего радиуса при условии, что скорость потока, выраженного в единицах объема на единицу времени, постоянна, а трубка имеет жесткие стенки, круглое сечение и один диаметр. В сообщении имеется вывод формулы Пузёйля, как самое распространённое, так и вывод по Лэмбу. Обсуждается применимость формулы Пуазёйля к гемодинамике. В капиллярах закон Пуазёйля не всегда выполняется. Известен так называемый эффект Фарейес-Линквиста (Fåhræus–Lindqvist effect) [1].

2. Вязкость крови

Вязкость крови — это биофизическое свойство крови, определяющее сопротивление потоку, и являющееся критическим фактором сосудистого сопротивления, преднагрузки, постнагрузки и перфузии тканей. Вязкость крови измеряют в паскаль-секундах (Па·с). Увеличение вязкости связано с уменьшением кровотока и повышением артериального давления и сосудистого сопротивления, тогда как уменьшение вязкости оказывает противоположный эффект. В видео объясняется соотношение вязкости, давления и объёма (плюс напряжение сдвига, скорость сдвига, к которым в настоящее время снова повысился интерес [2]). Рассматриваются типы жидкостей — ньютоновская, неньютоновская, бингамовская. Аномалии вязкости, Гематокрит — и остальное, вы увидите наглядно.

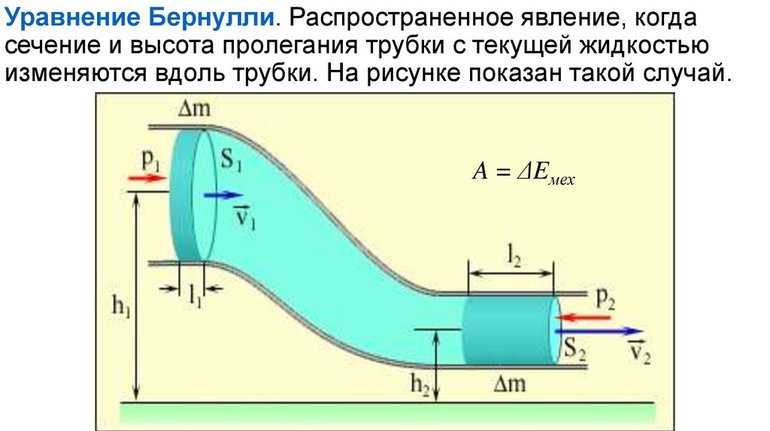
3. Уравнение Бернулли

Уравнение Бернулли — это количественное выражение принципа Бернулли, являющееся теоретическим описанием поведения так называемой идеальной жидкости (несжимаемой жидкости, у которой нет вязкости), утверждающего, что увеличение скорости жидкости происходит одновременно с уменьшением давления или уменьшением потенциальной энергии жидкости. Принцип является одним из основополагающих в гидродинамике, а следовательно и в гемодинамике. Примером практического использования в медицине может служить расчет чрезклапанного перепада давления, получаемый неинвазивно [3].

4. Боковое давление

Боковое давление — это давление, оказываемое заданным объемом жидкости при потоке в трубке, на её стенки, при исключении гравитационного потенциала и кинетической энергии этого объема. Концепция бокового давления возникла из принципа Бернулли. В гидромеханике чаще употребляют термин «статическое» давление. В гемодинамике это давление обсуждалось в научной литературе [4] в середине прошлого века, но широкого практического применения в медицине измерение бокового давления крови не получило.

5. Закон Торричелли

Закон Тoрричелли — это теорема в гидродинамике, связывающая скорость жидкости, вытекающей из отверстия, с высотой жидкости над отверстием. В видео имеется вывод уравнения Торричелли из уравнения Бернулли. В комментариях на Ютубе имеется небольшая, но интересная дискуссия. Наиболее важное клиническое использование уравнений из видео (или их модификаций) произошло в допплеровской эхокардиографии, в расчете градиента давления в суженных частях сердечно-сосудистой системы [5].

6. Гемодинамика в бифуркациях (основы)

Гемодинамика в бифуркациях — это физика тока крови через разветвляющиеся сосуды, в наиболее простом случае описывающая отношения между градиентом давления, скоростью потока и внутренним просветом в родительском стволе и дочерних ветвях. Изучается с использованием закона Мюррея и уравнения Дина. С геометрией артерий связано наличие атеросклеротических бляшек.

7. Что определяет сердечный выброс?

А про это видео подробности мной уже написаны здесь.

Литература:

1. Toksvang LN, Berg RM. Using a classic paper by Robin Fahraeus and Torsten Lindqvist to teach basic hemorheology. Adv Physiol Educ. 2013 Jun;37(2):129-33 [Pubmed]

2. Oshinski JN, Curtin JL, Loth F. Mean-average wall shear stress measurements in the common carotid artery. J Cardiovasc Magn Reson. 2006;8(5):717-22 [Pubmed]

3. Donati F, Myerson S, Bissell MM, et al. Beyond Bernoulli: Improving the Accuracy and Precision of Noninvasive Estimation of Peak Pressure Drops. Circ Cardiovasc Imaging. 2017 Jan;10(1). pii: e005207 [Pubmed]

4. Badeer HS. Hemodynamics for medical students. Adv Physiol Educ. 2001 Dec;25(1-4):44-52. Review. [Pubmed]

5. Poh KK, Levine RA, Solis J, et al. Assessing aortic valve area in aortic stenosis by continuity equation: a novel approach using real-time three-dimensional echocardiography. Eur Heart J. 2008 Oct;29(20):2526-35 [Pubmed]

Лекция 9

9. ТЕОРИЯ ЛАМИНАРНОГО ТЕЧЕНИЯ В КРУГЛОЙ ТРУБЕ

10.1. Потери напора на трение при ламинарном течении

10.2. Формула Вейсбаха-Дарси. Коэффициент Бусинеска.

10.3. Начальный участок ламинарного течения

10.4. Ламинарное течение в зазоре

10.5 Ламинарное течение в зазоре. Случай подвижных стенок.

10.6. Ламинарное течение в зазоре. Случай концентрических зазоров.

Рекомендуемые файлы

10.7. Особые случаи ламинарного течения. Течение c теплообменом

10.8. Течение при больших перепадах давления.

10.9. Течение с облитерацией.

10.1. Потери напора на трение при ламинарном течении.

Ламинарное течение является упорядоченным слоистым течением жидкости без перемешивания слоев.

Теория ламинарного течения основана на законе трения Ньютона, по которому касательное напряжение τ в жидкости определяется силой трения слоев друг о друга и о стенки

, , (10.1)

знак перед величиной касательного напряжения берется в зависимости от знака градиента скорости:

При ламинарном течении жидкости число Рейнольдса меньше 2300-4000 и в жидкости большую величину имеют силы вязкости в сравнении с силами инерции и силами тяжести, поэтому при выводах закономерностей, связанных с ламинарным течением эти силы не учитываются.

Для определения скоростей, расхода и потерь при ламинарном движении в прямой круглой трубе, расположенной горизонтально, с внутренним диаметром равным d = 2r_о, выделяют цилиндрический объем длиной l между сечениями «1-1» и «2-2», радиусом r, соосный с трубой и имеющий основания в выбранных сечениях.

В сечении «1 – 1» давление равно Р_1, а в сечении «2 – 2» равно Р₂. При постоянном внутреннем диаметре трубы скорость жидкости будет постоянной V₁=V₂ и коэффициент Кориолиса α не будет изменяться вдоль потока.

Уравнение Бернулли для выбранных сечений «1-1» и «2-2»

при z₁=z₂, V₁=V₂

,

где h_тр = Р_тр /(ρg), — потеря напора на трение по длине, эту величину показывают пьезометры, установленные в этих сечениях.

В уравнение равновесия выделенного объема жидкости входят силы давления и трения выделенного объема о слои окружающей жидкости.

При трении на поверхности цилиндра возникают касательные напряжения τ. Они действуют на цилиндрической поверхности и имея ввиду малость длины цилиндра можно считать, что напряжения равномерно распределены по его площади, поэтому уравнение равновесия цилиндра приобретает вид

. (10.2),

где Ртр =(Р₁-Р₂) –перепад давлений на основаниях цилиндра.

Из формулы следует, что касательные напряжения в поперечном сечении трубы изменяются по линейному закону в функции радиуса. Эпюры касательного напряжения показаны на рис. 10.1, в начале трубы.

Выразим касательное напряжение τ по закону трения Ньютона через динамическую вязкость и поперечный градиент скорости, при этом заменим переменное расстояние у от стенки текущим радиусом r :

Подставляя значение τ в предыдущее уравнение (10.2) , получим

Найдем отсюда дифференциал скорости

При положительном приращении радиуса получается отрицательное приращение (уменьшение) скорости, что соответствует профилю скоростей, показанному на рис. 10.1 в конце трубы.

Выполнив интегрирование, получим

Получим зависимость скорости от радиуса r

. (10.3)

Эта зависимость является законом распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой.

Максимальная скорость в центре сечения при r = 0 равна

(10.4)

Входящее в формулу (10.4) отношение (рис.10.1) называется пьезометрическим уклоном. Эта величина является постоянной вдоль прямой трубы постоянного диаметра при ламинарном течении с постоянной скоростью.

Элементарный расход выражается как произведение скорости на малую элементарную площадку δS:

Площадка dS берется в виде кольца радиусом r, и шириной δr, переходя к дифференциалам:

.

После интегрирования по всей площади поперечного сечения т. е. от r =0 до r = r₀

,

(10.5)

Среднюю по сечению скорость найдем делением расхода на площадь. С учетом выражения (10.5) получим

, (10.6)

Сравнение этого выражения с формулой показывает, что средняя скорость при ламинарном течении в 2 раза меньше максимальной : Vср = 0,5Vмакс.

Потери напора hтр на трение через расход и размеры трубы с учетом μ=νρ

, ( 10.7)

При ламинарном течении в трубе круглого сечения потеря напора на трение пропорциональна расходу и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон обычно называемый законом Пуазейля, используется для расчета потерь в трубопроводах при ламинарным течением.

Жорж Пуазейль — французский ученый, получил эту формулу (10.7) экспериментальным путем в 1840 г

10.2. Формула Вейсбаха-Дарси. Коэффициент Бусинеска

Потери напора на трение выражаются через среднюю скорость по формуле (10.6). Приведем формулу для потерь на трение к виду формулы Вейсбаха—Дарси:

для этого в формуле (10.7) выразим расход через среднюю скорость , и перегруппировав множители, после сокращении получим

, (10.7а)

Умножим числитель и знаменатель на V_ср получим

Формуле Вейсбаха-Дарси для определения потерь на трение при ламинарном движения

(10.8)

где — λ_л — коэффициент потерь на трение для ламинарного течения:

Потеря напора на трение по длине при ламинарном течении пропорциональна скорости в первой степени. Квадрат скорости в формуле (10.8) для ламинарного течения получен умножением и делением на V_ср, а коэффициент λ_л обратно пропорционален Re и, следовательно, скорости V_ср.

[Закон распределения скоростей по сечению трубы позволяет определить коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в уравнении Бернулли, для случая установившегося ламинарного течения жидкости в круглой трубе. Для этого в выражении для α заменим скорость по формуле и среднюю скорость по формуле (1.81), а также учтем, что dS = 2πrdr. После подстановок и сокращений получим

α =

Обозначив переменную 1 — r 2 /r₀ через z, найдем

α = — 8

Итак, действительная кинетическая энергия ламинарного потока с параболическим распределением скоростей в 2 раза превышает кинетическую энергию того же потока, но при равномерном распределении скоростей.

Таким же путем можно показать, что секундное количество движения ламинарного потока с параболическим распределением скоростей в 2 раза больше количества движения того же потока, но при равномерном распределении скоростей, причем коэффициент β, называемый коэффициентом Буссинеска, в данном случае равен 4/3.]

Изложенная теория ламинарного течения жидкости в круглой трубе хорошо подтверждается опытом, и выведенный закон сопротивления обычно не нуждается в каких-либо поправках, за исключением течения в начальном участке трубы, где происходит постепенное формирование параболического профиля скоростей.

2) при течении с теплообменом;

З) при течении в капиллярах и зазорах с облитерацией;

4) при течения с большими перепадами давления (пп. 2—4 рассмотрен в п. 1.27).

10.3. Начальный участок ламинарного течения

При ламинарном течении и подаче жидкости из резервуара в прямую трубу постоянного диаметра у входа в трубу распределение скоростей по сечению получается практически равномерным, особенно, если вход выполнен c закруглением (рис.10.2).

Затем под действием сил вязкости происходит перераспределение скоростей по сечениям: слои жидкости, прилежащие к стенке, тормозятся, а центральная часть потока, где еще сохраняется равномерное распределение скоростей, движется ускоренно.

При этом толщина слоев заторможенной жидкости постепенно увеличивается, пока не станет равной радиусу трубы, т. е. пока слои, прилегающие к противоположным стенкам, не сомкнутся на оси трубы. После этого устанавливается характерный для ламинарного течения параболический профиль скоростей.

Участок от начала трубы, на котором формируется параболический профиль скоростей, называется начальным участком течения — l_нач. За этим участком стабилизированное ламинарное течение, параболический профиль скоростей остается неизменным, как бы не была длинна труба, если сохраняется ее прямолинейность и постоянное сечения.

Теория ламинарного течения применима для этого стабилизированного ламинарного течения и неприменима для начального участка:

Для определения длины «начального участка» можно пользоваться приближенной формулой Шиллера, выражающей эту длину, отнесенную к диаметру трубы, как функцию числа Re:

Сопротивление на начальном участке трубы получается больше, чем на последующих участках. На начальном участке значение производной dv/dy у стенки трубы больше, чем на участках стабилизированного течения, больше и касательное напряжение, определяемое законом Ньютона.

Потеря напора на участке трубы, длина которого l ≤ l_нач определяется по формулам (10.7) или (10.8) с поправочным коэффициентом k>1. Значения этого коэффициента могут быть найдены по графику (рис.10.3), на котором он изображен как функция безразмерного параметра х*10 3 / (d*Re). С увеличением этого параметра коэффициент уменьшается и при значении

т. е. при х = l_нач, становится равным 1,09. Следовательно, сопротивление всего начального участка трубы на 9% больше, чем сопротивление такого же участка трубы, взятого в области стабилизированного ламинарного течения.

Для коротких труб значения поправочного коэффициента, как видно из графика, весьма существенно отличаются от единицы.

Учитывая формулы (10.7) и (10.8) и выполняя соответствующие преобразования, получаем

(10.12)

Если относительная длина l/d трубы трубопровода велика, то дополнительный член в скобках, равный 0,165 можно ввиду малости не учитывать. Однако, при уточненном расчете труб, длина которых соизмерима с l_нач этот член следует учитывать. Для начального участка трубы с плавным входом коэффициент Кориолиса α возрастает от единицы до двух.

10.4. Ламинарное течение в зазоре

Определим скорость, расход и потери при ламинарном течении в зазоре, образованном двумя параллельными плоскими стенками, расстояние между которыми равно а (рис. 10.4). Начало координат поместим в середине зазора, направив ось Ох вдоль течения, а ось Оу — по нормали к стенкам.

Возьмем два нормальных поперечных сечения потока на расстоянии l одно от другого и рассмотрим поток шириной, равной единице. Выделим объем жидкости в форме прямоугольного параллелепипеда, расположенного симметрично относительно оси Ох между выбранными поперечными сечениями потока и имеющего размеры сторон l*2y*b, где b=1.

Условие равномерного движения выделенного объема вдоль оси Ох:

где р_тр = р₁— р₂ – разность давлений(перепад) в рассматриваемых сечениях. Знак минус, потому что производная ∂V/∂y отрицательна, 2l*b, так как две поверхности – сверху и снизу

Из предыдущего (10.13) найдем приращение скорости ∂V, соответствующей приращению координаты ∂y:

После интегрирования получим:

Так как на стенке y = a/2, V = 0, находим C = , откуда

, (10.13)

Далее подсчитаем расход q, приходящийся на единицу ширины потока, для чего возьмем симметрично относительно оси Оz две элементарные площадки 2b*δy = 2δy, так как b=1 и выразим элементарный расход

перейдя к дифференциалам и интегрируя, получим

Выразим потерю давления на трение через полный расход Q= q*b при зазоре шириной b ≠ 1; получим

(10.14)

10.5. Ламинарное течение в зазоре. Случай подвижных стенок.

Когда одна из стенок, образующих зазор, перемещается параллельно другой стенке, а давление в зазоре постоянно вдоль длины, подвижная стенка увлекает за собой жидкость, и возникает так называемое фрикционное безнапорное движение.

Выделим в таком потоке элемент dx*dy*b, как показано на рис. 10.5 и рассмотрим действующие на него силы.

Давления, приложенные к левой и правой граням элемента одинаковы (напора – нет), на элемент действуют только силы трения, вызываемые касательными напряжениями на верхней грани — τ на нижней грани τ+δτ.

Для того чтобы имело место равновесие, эти силы должны быть равны и τ = С.

По закону Ньютона τ = — μdv/dy = C (знак минус взят т.к. при dy > 0, dv ’ _л =kλ _л т. е.

где k — поправочный коэффициент, зависящий от формы сечения.

Для прямоугольного сечения (a*b)Dг = 2ab/(а +b), а к = f(b/a)

Для сечения в форме равностороннего треугольника со сторонами а k= 0,83.

10.7. Особые случаи ламинарного течения. Течение е теплообменом

Течение е теплообменом. В рассмотренных выше случаях ламинарного течения не учитывалось изменение температуры и, следовательно, влияние вязкости жидкости, как в пределах поперечного сечения, так и вдоль потока, т. е предполагалось постоянство температуры во всех точках потока. Подобное течение в отличие от течений, сопровождающихся изменением температуры жидкости, называют изотермическим.

Если по трубопроводу движется жидкость, температура которой значительно выше температуры окружающей среды, то такое течение сопровождается теплоотдачей через стенку трубы во внешнюю среду и, следовательно, охлаждением жидкости. Когда же температура движущейся жидкости ниже температуры окружающей среды, происходит приток тепла через стенку трубы, в результате жидкость в процессе течения нагревается.

Таким образом, при течении жидкости происходит теплообмен с внешней средой, следовательно, температура жидкости, а также ее вязкость не сохраняются постоянными, а течение не является изотермическим. Поэтому формулы (1.88) и (1 .8), полученные в предположении постоянства вязкости по сечению потока, при течении жидкости со значительным теплообменам нуждаются в поправках.

При течении, сопровождающемся охлаждением жидкости, ее слои, непосредственно прилегающие к стенке, имеют температуру более низкую, а вязкость более высокую, чем основное ядро потока. Вследствие этого происходит более интенсивное торможение пристенных слоев жидкости и снижение градиента скорости у стенки. При течении сопровождающемся нагреванием жидкости обусловленным притоком тепла через стенку, пристенные слои жидкости имеют более высокую температуру и пониженную вязкость, вследствие чего градиент скорости у стенки более высокий. Таким образом, вследствие теплообмена через стенку трубы между жидкостью и внешней средой нарушается рассмотренный выше параболический закон распределения скорости.

На рис. 1.51 показаны сравнительные графики распределения скоростей: при Изотермическом течении (1), при течении с охлаждением (2) и с нагреванием (3) жидкости, но при одинаковом расходе и при одинаковой вязкости жидкости в ядре потока. Из рисунка видно, что охлаждение жидкости влечет за собой увеличение неравномерности распределения скоростей (α > 2), а нагревание — уменьшение этой неравномерности (α αp ₁.

Для изотермического течения в формуле (1.97) следует положить k=0 . С учетом предыдущего в этом случае, получим

Найдем относительный расход q, равный отношению расхода при переменной вязкости и расходу при μ = μ₀ = const. Для этого разделим уравнение (1.97) на

Q0 = P1*ab/(12 μ₀l) и получим

На рис. 1.52 представлены зависимости от Р₁ по формуле (1.99) для трех жидкостей : керосина(1), трансформаторного масла (2) и жидкости АМГ-10(3), причем для двух случаев : k=1 отсутствие теплообмена) и k = 0 (изотермическое течение). Кривые, соответствующие двум крайним режимам, расходятся довольно существенно. Реальные процессы описываются кривыми, которые располагаются между этими предельными кривыми. В связи с тем, что скорости течения жидкости в зазорах при столь высоких перепадах давления очень велики и каждая частица пребывает в зазоре вес ьма незначительное время, более вероятными представляется режим течения , при котором k = 1 т.е. теплообмен играет незначительную роль. Это предположение подтверждается новыми экспериментами по исследованию изотермического течения в зазорах, проведенными Солиным. Однако, эти же исследования показывают, что при увеличении относительной длины зазора l/a и числа Прандтля, равного Pr= μc/λ (c – теплоемкость, λ — коэффициент теплопроводности, а также при уменьшении числа Re роль теплообмена возрастает, и процесс течения может приближаться к изотермическому.

Изложенная теория позволяет получить зависимость Р/Р1 от x/l и построить соответствующие кривые (рис.1.53) Как видно из графика, чем выше давление Р1 тем больше отклонение кривых от прямой , соответствующей закону Пуазейля.

10.9. Течение с облитерацией.

Иногда при течении через капилляры и малые зазоры наблюдается явление, которое может, не быть объяснено законами гидравлики. Оно заключается в том, что расход жидкости через капилляр или зазор с течением времени уменьшается, несмотря на то, что перепад давления, под которым происходит движение жидкости, и ее физические свойства остаются неизменными. В отдельных случаях движение жидкости по истечении некоторого времени может прекратиться полностью. Это явление носит название облитерации, и его причина заключается в том, что при определенных условиях уменьшается площадь поперечного сечения канала (зазора, капилляра), вследствие, адсорбции (отложения) полярноактивных молекул жидкости на его стенках.

Толщина адсорбционного слоя для масел составляет несколько микрометров, поэтому при течении через капилляры и малые зазоры этот слой может существенно уменьшить площадь поперечного сечения или даже полностью перекрыть его.

Уравнение Бернулли — вывод формулы, физический смысл, примеры использования

Исследования учёного

Даниил Бернулли родился в Голландии в 1700 году. В 1725 году он начал работать на кафедре физиологии, где увлёкся основами теоретической физики. Через 25 лет он возглавил кафедру экспериментальной физики, которой и руководил до конца своих дней. Основным его трудом считается создание теории гидродинамической зависимости, известной как Закон Бернулли. Открытие учёного предвосхитило зарождение молекулярно-кинетического учения поведения газов.

Причиной открытия принципа стало изучение действия закона сохранения энергии в различных ситуациях. Бернулли установил, что давление жидкости в замкнутом пространстве зависит от сечения объекта, в котором она находится. Чем меньше сечение трубы, тем ниже будет созданное давление в пропускаемом через неё жидком веществе.

Этот факт был доказан экспериментально и описан математически.

Правило в математической формулировке имеет вид (pv 2 / 2) + p * g * h + ρ = const, где:

• p — количество жидкости на единицу объёма;
• v — скорость движения потока;
• h — уровень, на который поднят элемент жидкости;
• ρ — сила, действующая на единицу площади;
• g — ускорение, придаваемое жидкости под действием притяжения Земли.

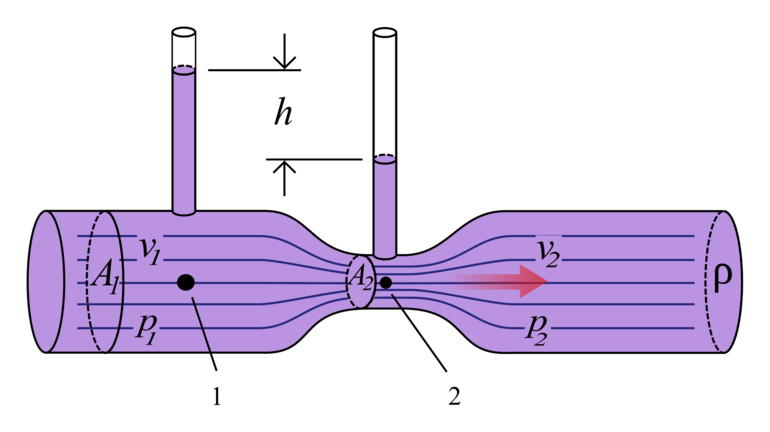
Чтобы понять физический смысл уравнения Бернулли, нужно рассмотреть трубу переменного сечения, в которой существует точка А и Б. Первая располагается в широкой части, а вторая — в узкой. В соответствии с уравнением непрерывности скорость V1 в части трубы, имеющей большее сечение, будет меньше, чем скорость жидкости V2 в узком сечении. Если в жидкость поместить прибор для измерения давления, он покажет какое-то значение P1 в точке A и P2 в точке Б. При этом там, где скорость движения жидкости медленнее, давление будет больше.

Объясняется это следующим образом: если V1 больше V2, значит, при движении происходит изменение скорости течения. Представив, что в жидкости находится точка, можно утверждать о её движении с ускорением. Это означает, что на неё действуют силы.

Одна из них совпадает с направлением течения, тем самым ускоряя движение. Обусловлена эта сила разностью давления.

Так как движение происходит от точки А к Б, то и давление возле А будет больше, чем около Б. Эта разность давлений и приводит к ускорению.

Условия действия

Закон применим для условия, при котором соблюдается неразрывность струи воздуха или жидкости. В тех участках потока, где скорость течения больше, давление будет меньше и наоборот. Это утверждение и называется теоремой Бернулли. По сути, закон позволяет установить связь между давлением, скоростью, высотой.

Пусть имеется труба переменного сечения с изменяющейся высотой. Внизу она широкая, а затем сужается. По ней течёт жидкость. Площадь сечения можно обозначить как S1 и S2, а давление участков и скорость движения на них P1, P2, V1, V2. Высота внизу будет равняться S1, а вверху S2.

Выделив участок в трубе с жидкостью, можно сказать, что она движется слева направо и через некоторое время полностью сдвинется в область S2. Изменение положения слева будет равно расстоянию дельта L1, а справа — дельта L2.

Течение является:

• ламинарным — находящаяся в трубке жидкость перемешивается слоями без хаотических изменений давления и скорости, турбулентность отсутствует;
• стационарным — распределение скоростей не изменяется с течением времени;
• скоростным — в движении принимает участие такой параметр, как ускорение;
• идеальным с несжимаемой жидкостью.

Последнее обозначает, что нет вязкости. Поэтому на жидкость действует только сила упругости и тяжести, а силы трения нет. Система не является замкнутой, а значит закон сохранения энергии применительно к рассматриваемому участку использовать нельзя. Зато вполне можно применить теорему о кинетической энергии.

Для газов уравнение можно использовать лишь в том случае, если их плотность изменяется незначительно. Но касаемо аэродинамики учитывается и то, что изменение давления воздуха гораздо меньше атмосферного. Поэтому уравнение можно применять в аэродинамических расчётах.

Согласно ему, сумма действующих всех сил на тело (рассматриваемый кусок жидкости) равняется изменению кинетической энергии объекта: ΣAi = ΔEk. На нижний участок действует сила давления, выполняющая положительную работу, а на верхний — отрицательную. Кроме этого, действует и сила тяжести. Так как жидкость поднимается, она имеет тоже отрицательный знак. Сила бокового давления перпендикулярна любой точке в системе, поэтому никакого влияния она не оказывает.

Количественная сторона

Исходя из сил, действующих на тело, изменение кинетической энергии можно описать выражением: ΔEk = Ap1 +Ap2 +Ag. Чтобы найти работу, необходимо силу умножить на пройденное расстояние. Поэтому работа силы давления равна произведению самой силы F на модуль перемещения ΔL и косинусу угла между ними: Ap1 = F1* ΔL *1.

Чтобы найти силу, нужно давление умножить на площадь. Значит: Ap1 = p 1 * S1 * ΔL1 = p1V1. Таким же образом находится работа для второго состояния: Ap2 = F1* ΔL2 *(-1) = — p2 * S2 * ΔL2 = -p2 * V2. Жидкость несжимаемая, следовательно: V1=V2=V.

Работу силы тяжести можно вычислить исходя из того, что рассматриваемый кусок жидкости является относительным, то есть он, хотя и не статический, в любом месте будет подвергаться воздействию одинаковой силы тяжести. Верным будет выражение: Ag = — ΔEp = — (m2 * g * h2 — m1 * g * h1) = m1 * g * h1 — m2 * g * h2. Так как жидкость несжимаемая, её плотность не изменится. Отсюда можно утверждать: Ag = ρ * V * g * h1 — ρ * V * g * h2.

Зная количественные показатели всех трёх работ, можно найти изменение кинетической энергии. Из физики известно, что оно равно разнице конечной и начальной энергии. Течение стационарное, значит, скорость с течением времени не изменится. Следовательно, кинетическая энергия будет определяться разницей появившейся энергии в верхней части и ушедшей из нижней области: ΔEk = (m2 * v2 2 )/2 — (m1 * v1 2 ) / 2.

Воспользовавшись тем, что масса равняется произведению плотности на объём, формулу можно привести к виду: ΔEk = (ρ * V * v2 2 )/2 — (ρ * V * v1 2 ) / 2. Теперь найденные выражения для работ нужно подставить в теорему о кинетической энергии. Получится следующее равенство: p1V — p2V + ρ * V * g * h1 — ρ * V * g * h2 = (ρ * V * v2 2 ) / 2 — (ρ * V * v1 2 ) / 2. Разделив левую и правую часть на объём, выражение можно упростить до вида: p1 — p2 + ρ * g * h1 — ρ * g * h2 = (ρ * v2 2 )/2 — (ρ * v1 2 ) / 2 .

То место, где давление p1, некая точка внутри трубки, пусть будет обозначено цифрой один, а там, где p2, — цифрой два. Всё что относится к единице можно записать в левой части, а к двойке — в правой: ρ1 * g * h1 + (ρ * v1 2 ) / 2 = ρ * g * h2 + (ρ * v2 2 ) / 2. Полученная формула показывает, что при переходе в пределе одной линии скорость, давление и высота изменяются. Поэтому в любой точке будет справедливым выражение: ρ1+ ρ * g * h + (ρ * v1) / 2 = const. Это и есть количественное описание уравнения Бернулли для идеальной жидкости.

Применение в гидравлике

Наиболее типичным примером использования уравнения является решение заданий по нахождению скорости вытекания жидкости из отверстия в широком сосуде. Такой ёмкостью называют систему, в которой диаметр сосуда значительно больше размера отверстия. Необходимо найти скорость вытекающей жидкости U1. Известно, что высота столба жидкости, на который действует сила тяжести g, равна h.

Пусть в жидкости, находящейся сверху, имеется точка один. Через некоторое время она окажется внизу в положении два. На верх жидкости давит атмосферное давление, поэтому p1=pатм. Высота в точке один равна h. Скорость U1 считают равной нулю. Давление p2 в точке два будет также равно атмосферному. Так как жидкость опустится на дно, то высота h2 станет нулевой.

Все эти величины следует подставить в уравнение Бернулли. Получится выражение: pатм + ρ * g * h + 0 = pатм + (ρ * U 2 ) / 2 + 0. Атмосферное давление взаимно уничтожается: ρ * g * h = (ρ * U 2 ) / 2. В левой и правой части стоит плотность, на которую можно сократить. Отсюда получается, что вид жидкости значения не имеет. Это может быть: вода, ртуть, расплавленный металл. Эффект от этого не поменяется. Из формулы можно выразить искомое U2. Оно будет равно: U2 = (2 * g * h) ½ .

Интересным фактом является то, что полученный ответ при решении задачи называется формулой Торричелли. Она показывает, что скорость, с которой вытекает жидкость из широкого сосуда, равна скорости тела при свободном падении с той же высоты.

Используя уравнение, можно легко рассчитать давление жидкости на дно и стенки сосуда. В этом случае закон Бернулли является обобщением для формулы гидростатического давления. Пусть имеется сосуд с жидкостью высотой h. Точка, находящаяся наверху, характеризуется давлением p1 = pатм., высотой h1 равной h и скоростью U1. Для точки на дне параметры будут следующие: p2 = p, h2 = 0, U2 = 0. Скорости принимаются равными нулевому значению, так как рассматриваемая жидкость находится в состоянии покоя.

Данные следует подставить в уравнение. В итоге получится равенство: pатм + ρ * g * h + 0 = p + 0 + 0. Из него несложно найти неизвестное: p = pатм + ρ * g * h. Полученный ответ является формулой гидростатического давления и подтверждает закон Паскаля.

Аналогично уравнение Бернулли для потока реальной жидкости используется при расчёте расхода в карбюраторе, пульверизаторе, учёте статического и динамического давления.

Подъёмная сила

Самолёт летает благодаря тому, что набегающий на крыло напор воздуха создаёт подъёмную силу. Её можно рассчитать и оценить с помощью уравнения. Геометрически крыло можно представить в виде плоскости с углом a (угол атаки). На него действует поток воздуха со скоростью U. Частица воздуха ударяет в твёрдую поверхность и отражается от неё. Угол отражения равен углу атаки, а её скорость равняется U’. Нужно рассчитать подъёмную силу. Для этого необходимо выполнить три шага:

• рассмотреть изменение скорости воздуха;
• узнать импульс частиц;
• используя закон Ньютона, определить силу.

В результате получится, что на крыло действует сила, состоящая из двух компонентов: подъёмной силы Fy и аэродинамического сопротивления Fx. Fy = Cy * p * U 2 * S, а Fx = Cx * p * U 2 * S. В формулах С является коэффициентом, а S — площадью крыла.

Для расчёта используется уравнение Бернулли. Выглядеть оно будет следующим образом: Pп. к + (ρ * Uп. к) * 2 / 2 + ρ * g * hп. к = Pн. к + (ρ * Uн. к) * 2 / 2 + ρ * g * hн. к, где: п. к — под крылом, а н. к — над крылом. Это уравнение можно упростить, приняв, что давления над и под крылом примерно одинаковые, поэтому плотность будет также одинаковая. Кроме того, высота крыла довольно маленькая. Исходя из этого, формулу можно упростить, и она примет вид: pп. к-pн.к = (ρ * (Uн.к + Uп. к) * (Uн.к — Uп. к)) / 2 = 2 * U1 * U2. Теперь можно найти подъёмную силу. Для этого разность давлений нужно умножить на площадь крыла: Fy = (pп.к-pн. к) * S.

Таким образом, используя метод, можно рассчитать подъёмную силу, обусловленную эффектом Бернулли. Например, пусть дано, что площадь крыла равна 50 м². Скорость потока воздуха над крылом и под ним соответственно равны: U1 = 320 м/с, U2 = 290 м/с. Найти грузоподъёмность. Для решения задания нужно знать дифференциальную плотность воздуха. Это справочная величина, равная 1,29 кг/м3.

Используя уравнение Бернулли, можно записать: pп. к-pн.к = ρ * (U2н.к — U2п. к). Подъёмная сила равна площади крыла, умноженной на разность давления. Подставив одно выражение в другое, получим рабочую формулу: Fy = ρ * (U2н.к — U2п. к) * S / 2. После выполнения расчёта получится ответ 590 кН. То есть грузоподъёмность самолёта составит порядка 59 тонн.

Реальные вычисления для таких задач довольно сложные, поэтому часто используют онлайн-калькуляторы.