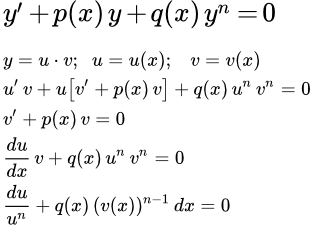Уравнение бернулли примеры и их решение

Дифференциальное уравнение Бернулли и методы его решения

Решение дифференциального уравнения Бернулли приведением к линейному уравнению

Рассмотрим дифференциальное уравнение Бернулли:
(1) ,
где n ≠ 0 , n ≠ 1 , p и q – функции от x .
Разделим его на y n . При y ≠ 0 или n 0 имеем:
(2) .
Это уравнение сводится к линейному с помощью замены переменной:
.
Покажем это. По правилу дифференцирования сложной функции:
;
.
Подставим в (2) и преобразуем:
;
.
Это – линейное, относительно z , дифференциальное уравнение. После его решения, при n > 0 , следует рассмотреть случай y = 0 . При n > 0 , y = 0 также является решением уравнения (1) и должно входить в ответ.

Решение методом Бернулли

Рассматриваемое уравнение (1) также можно решить методом Бернулли. Для этого ищем решение исходного уравнения в виде произведения двух функций:
y = u·v ,
где u и v – функции от x . Дифференцируем по x :
y′ = u′ v + u v′ .
Подставляем в исходное уравнение (1):
;
(3) .
В качестве v возьмем любое, отличное от нуля, решение уравнения:
(4) .
Уравнение (4) – это уравнение с разделяющимися переменными. Решаем его и находим частное решение v = v ( x ) . Подставляем частное решение в (3). Поскольку оно удовлетворяет уравнению (4), то выражение в круглых скобках обращается в нуль. Получаем:
;
.
Здесь v – уже известная функция от x . Это уравнение с разделяющимися переменными. Находим его общее решение, а вместе с ним и решение исходного уравнения y = uv .

Примеры решений дифференциального уравнения Бернулли

Пример 1

Решить уравнение
(П1.1)

Это дифференциальное уравнение Бернулли. Решаем его методом Бернулли. Ищем решение в виде произведения двух функций: . Тогда
. Подставляем в (П1.1):
;
(П1.2) .
Одну из этих функций мы можем выбрать произвольным образом. Выберем v так, чтобы выражение в круглых скобках равнялось нулю:
(П1.3) .
Тогда подставляя (П1.3) в (П1.2), мы получим дифференциальное уравнение с разделяющимися переменными:
(П1.4) .

Сначала мы определим функцию v . Нам нужно найти любое, отличное от нуля, решение уравнения (П1.3). Решаем его. Для этого разделяем переменные и интегрируем.
;
;
;
;
.
Отсюда , или . Возьмем решение с и знаком ′плюс′. Тогда , или .

Итак, мы нашли функции u и v . Находим искомую функцию y :
.
Заменим постоянную интегрирования: . Тогда общее решение исходного уравнения (П1.1) примет вид:
.

Когда мы делили на u , то предполагали, что . Теперь рассмотрим случай . Тогда . Нетрудно видеть, что постоянная функция также является решением исходного уравнения (П1.1) ⇑.

Общее решение уравнения: .
Уравнение также имеет решение .

Пример 2

На первый взгляд, кажется, что это дифференциальное уравнение не похоже на уравнение Бернулли. Если считать x независимой переменной, а y – зависимой (то есть если y – это функция от x ), то это так. Но если считать y независимой переменной, а x – зависимой, то легко увидеть, что это – уравнение Бернулли.

Итак, считаем что x является функцией от y . Подставим в исходное уравнение и умножим на :
;
;
(П2.1) .
Это – уравнение Бернулли с n = 2 . Оно отличается от рассмотренного выше, уравнения (1), только обозначением переменных ( x вместо y ). Решаем методом Бернулли. Делаем подстановку:
x = u v ,
где u и v – функции от y . Дифференцируем по y :
.
Подставим в (П2.1):
;
(П2.2) .
Ищем любую, отличную от нуля функцию v ( y ) , удовлетворяющую уравнению:
(П2.3) .
Разделяем переменные и интегрируем:
;
;
.
Поскольку нам нужно любое решение уравнения (П2.3), то положим C = 0 :
; ; .
Возьмем решение со знаком ′плюс′:
.
Подставим в (П2.2) учитывая, что выражение в скобках равно нулю (ввиду (П2.3)):
;
;
.
Разделяем переменные и интегрируем. При u ≠ 0 имеем:
;
(П2.4) ;
.
Во втором интеграле делаем подстановку :
;
.
Интегрируем по частям:
;
.
Подставляем в (П2.4):
.
Возвращаемся к переменной x :
;
;
.

Автор: Олег Одинцов . Опубликовано: 07-08-2012 Изменено: 29-10-2020

Примеры решений задач на формулу Бернулли

Калькуляторы на формулу Бернулли

Обратите внимание на следующие разделы, где разобраны типовые задачи на формулу Бернулли. Вы можете решить или проверить вычисления своих заданий с помощью онлайн-калькуляторов. Теорию по этой теме можно найти в онлайн-учебнике.

Схема Бернулли: решенные задачи

Задача 1. Из $n$ аккумуляторов за год хранения $k$ выходит из строя. Наудачу выбирают $m$ аккумуляторов. Определить вероятность того, что среди них $l$ исправных.
$n = 100, k = 7, m = 5, l = 3.$

Задача 2. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:
а) три элемента;
б) не менее четырех элементов;
в) хотя бы один элемент.

Задача 3. Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?

Задача 5. Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) не более одного потребует ремонта; б) хотя бы один не потребует ремонта.

Задача 6. Что более вероятно выиграть у равносильного противника: не менее двух партий из трёх или не более одной из двух?

Задача 7. а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4;
б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8.

Формула Пуассона: решенные задачи

Задача 4. С базы в магазин отправлено 4000 тщательно упакованных доброкачественных изделий. Вероятность того, что изделие повредится в пути, равна 0.0005. Найти вероятность того, что из 4000 изделий в магазин прибудут 3 испорченных изделия.

Задача 8. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено:
а) три ошибочно укомплектованных пакета;
б) не более трех пакетов.

Дифференциальное уравнение Бернулли

Статья раскрывает методы решения дифференциального уравнения Бернулли. В заключении будут рассмотрены решения примеров с подробным объяснением.

Приведение к линейному уравнению 1 порядка

Дифференциальное уравнение Бернулли записывается как y ‘ + P ( x ) · y = Q ( x ) · y n . Если n = 1 , тогда его называют с разделяющими переменными. Тогда уравнение запишется как y ‘ + P ( x ) · y = Q ( x ) · y ⇔ y ‘ = Q ( x ) — P ( x ) · y .

Для того, чтобы решить такое уравнение, необходимо первоначально привести к линейному неоднородному дифференциальному уравнению 1 порядка с новой переменной вида z = y 1 — n . Проделав замену, получаем, что y = z 1 1 — n ⇒ y ‘ = 1 1 — n · z n 1 — n · z ‘ .

Отсюда вид уравнения Бернулли меняется:

y ‘ + P ( x ) · y = Q ( x ) · y n 1 1 — n · z 1 1 — n · z ‘ + P ( x ) · z 1 1 — n = Q ( x ) · z 1 1 — n z ‘ + ( 1 — n ) · P ( x ) · z = ( 1 — n ) · Q ( x )

Этот процесс вычисления и подстановки способствует приведению к линейному неоднородному дифференциальному уравнению первого порядка. В итоге проводим замену и получаем его решение.

Найти общее решение для уравнения вида y ‘ + x y = ( 1 + x ) · e — x · y 2 .

Решение

По условию имеем, что n = 2 , P ( x ) = x , Q ( x ) = ( 1 + x ) · e — x . Необходимо ввести новую переменную z = y 1 — n = y 1 — 2 = 1 y , отсюда получим, что y = 1 z ⇒ y ‘ = — z ‘ z 2 . Провести замену переменных и получить ЛНДУ первого порядка. Запишем, как

y ‘ + x y = ( 1 + x ) · e — x · y 2 — z ‘ z 2 + x z = ( 1 + x ) · e — x · 1 z 2 z ‘ — x z = — ( 1 + x ) · e — x

Следует проводить решение при помощи метода вариации произвольной постоянной.

Проводим нахождение общего решения дифференциального уравнения вида:

d z d x — x z = 0 ⇔ d z z = x d x , z ≠ 0 ∫ d z z = ∫ x d x ln z + C 1 = x 2 2 + C 2 e ln z + C 1 = e x 2 2 + C 2 z = C · e x 2 2 , C = e C 2 — C 1

Где z = 0 , тогда решение дифференциального уравнения считается z ‘ — x z = 0 , потому как тождество становится равным нулю при нулевой функции z . Данный случай записывается как z = C ( x ) · e x 2 2 , где С = 0 . Отсюда имеем, что общим решением дифференциального уравнения z ‘ — x z = 0 считается выражение z = C · e x 2 2 при С являющейся произвольной постоянной.

Необходимо варьировать переменную для того, чтобы можно было принять
z = C ( x ) · e x 2 2 как общее решение дифференциального уравнения вида z ‘ — x z = — ( 1 + x ) · e — x .

Отсюда следует, что производится подстановка вида

C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · e x 2 2 ‘ — x · C ( x ) · e x 2 2 = — 1 + x · e — x C ‘ ( x ) · e x 2 2 + C ( x ) · x · e x 2 2 — x · C ( x ) · e x 2 2 = — ( 1 + x ) · e — x C ‘ ( x ) · e x 2 2 = — ( 1 + x ) · e — x 2 2 — x C ( x ) = ∫ — ( 1 + x ) · e — x 2 2 — x d x = ∫ e — x 2 2 — x d — x 2 2 — x = e — x 2 x — x + C 3

С 3 принимает значение произвольной постоянной. Следовательно:

z = C x · e x 2 2 = e — x 2 2 — x + C 3 · e x 2 2 = e — x + C 3 · e x 2 2

Дальше производится обратная замена. Следует, что z = 1 y считается за y = 1 z = 1 e — x + C 3 · e x 2 2 .

Ответ: это решение считается решением исходного дифференциального уравнения Бернулли.

Представление произведением функций u ( x ) и v ( x )

Имеется другой метод решения дифференциального уравнения Бернулли, который основывается на том, что функцию представляют при помощи произведения функций u ( x ) и v ( x ) .

Тогда получаем, что y ‘ = ( u · v ) ‘ = u ‘ · v + u · v ‘ . Производим подстановку в уравнение Бернулли y ‘ + P ( x ) · y = Q ( x ) · y n и упростим выражение:

u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) · u · v n u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · u · v n

Когда в качестве функции берут ненулевое частное решение дифференциального уравнения v ‘ + P ( x ) · v = 0 , тогда придем к равенству такого вида

u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x ) · ( u · v ) n ⇔ u ‘ · v = Q ( x ) · ( u · v ) n .

Отсюда следует определить функцию u .

Решить задачу Коши 1 + x 2 · y ‘ + y = y 2 · a r c t g x , y ( 0 ) = 1 .

Решение

Переходим к нахождению дифференциального уравнения вида 1 + x 2 · y ‘ = y · a r c t g x , которое удовлетворяет условию y ( 0 ) = 1 .

Обе части неравенства необходимо поделить на x 2 + 1 , после чего получим дифференциальное уравнение Бернулли y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

Перейдем к поиску общего решения.

Принимаем y = u · v , отсюда получаем, что y ‘ = u · v ‘ = u ‘ · v + u · v ‘ и уравнение запишем в виде

y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + u · v x 2 + 1 = u · v 2 · a r c t g x x 2 + 1 u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c t g x x 2 + 1

Проведем поиск частного решения с наличием разделяющих переменных v ‘ + v x 2 + 1 = 0 , отличных от нуля. Получим, что

d v v = — d x x 2 + 1 , v ≠ 0 ∫ d v v = — ∫ d x x 2 + 1 ln v + C 1 = — a r c t g x + C 2 v = C · e — a r c t g x , C = e C 2 — C 1

В качестве частного решения необходимо брать выражение вида v = e — a r c r g x . Преобразуем и получим, что

u ‘ · v + u · v ‘ + v x 2 + 1 = u 2 · v 2 · a r c r g x x 2 + 1 u ‘ · v + u · 0 = u 2 · v 2 · a r c t g x x 2 + 1 u ‘ = u 2 · v · a r c t g x x 2 + 1 u ‘ = u 2 · e — a r c t g x · a r c t g x x 2 + 1 ⇔ d u u 2 = e — a r c t g x · a r c t g x x 2 + 1 d x , u ≠ 0 ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x x 2 + 1 d x ∫ d u u 2 = ∫ e — a r c t g x · a r c t g x d ( a r c t g x )

Имеем, что u = 0 рассматривается как решение дифференциального уравнения. Далее необходимо решить каждый из полученных интегралов по отдельности.

Интеграл с левой стороны, имеющего вид ∫ d u u 2 , необходимо найти по таблице первообразных. Получаем, что

∫ d u u 2 = — 1 u + C 3 .

Чтобы найти интеграл вида ∫ e — a r c t g x · a r c t g x d ( a r c t g x ) , принимаем значение a r c t g x = z и применяем метод интегрирования по частям. Тогда имеем, что

∫ e — a r c t g x · a r c t g x d ( a r c t g x ) = a r c t g x = z = = ∫ e — z · z d z = u 1 = z , d v 1 = e — z d z d u 1 = d z , v 1 = — e — z = = — z · e — z + ∫ e — z d z = — z · e — z — e — z + C 4 = = — e — z · ( z + 1 ) + C 4 = — e — a r c t g x · ( a r c t g x + 1 ) + C 4

— 1 u + C 3 = — e — a r c t g x · a r c t g x + 1 + C 4 1 u = e — a r c r g x · a r c t g x + 1 + C 3 — C 4 u = 1 e — a r c r g x · ( a r c t g x + 1 ) + C

Отсюда находим, что

y = u · v = e — a r c t g x e — a r c r g x · ( a r c t g x + 1 ) + C и y = 0 · v = 0 · e — a r c r g x = 0 являются решениями дифференциального уравнения Бернулли вида y ‘ + y x 2 + 1 = y 2 · a r c t g x x 2 + 1 .

На данном этапе следует переходить к поиску частного решения, которое удовлетворяет начальному условию. Получим, что

y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + C , тогда запись примет вид y 0 = e — a r c t g 0 e — a r c t g 0 · a r c t g 0 + 1 + C = 1 1 + C .

Очевидно, что 1 1 + C = 1 ⇔ C = 0 . Тогда искомой задачей Коши будет являться полученное уравнение вида y = e — a r c t g x e — a r c t g x · a r c t g x + 1 + 0 = 1 a r c t g x + 1 .