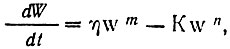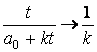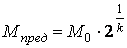Уравнение берталанфи уравнение роста имеет вид

Уравнение Берталанфи

Уравнение Берталанфи (1957) — применяется для определения роста животных, в частности, рыб, по формуле:

где W — масса организма, n — константа анаболизма, К — константа катаболизма. Показатель степени п Берталанфи приравнивал к единице.

1. Козлов В.И., Абрамович Л.С. Краткий словарь рыбовода.- М.: Россельхозиздат, 1982.- 160 с.

Уравнение берталанфи уравнение роста имеет вид

ЗАКОНОМЕРНОСТИ РОСТА БИОЛОГИЧЕСКИХ ОБЪЕКТОВ

Анализ экспериментальных данных по росту живых организмов позволяет сделать вывод о том, что рост всего живого подчиняется простой формуле, содержащей 2 параметра, различием которых с количественной точки зрения объясняется все многообразие животного и растительного мира.

Введение. Проблема роста живых организмов составляет одну из фундаментальных проблем биологии развития. Эта проблема связана с такими областями теоретической биологии, как старение организмов, регенерация органов и тканей, злокачественный рост, рост популяций и т.д. Знание закономерностей роста чрезвычайно важно для практики, т .к этот процесс связан с проблемами сельского хозяйства и медицины.

Для описания роста с количественной, математической точки зрения исследователями в разное время предлагались разные формулы и уравнения.

Наиболее известные из них:

1. Формула Гомпертца. Английский математик Бенджамин Гомпертц (1779 – 1865) в 20-х годах 19-го века предложил формулу для характеристики смертности людей в зависимости от возраста, которая затем была применена для описания роста животных.

2. Уравнение Берталанфи. Людвиг фон Берталанфи (1901 – 1972), австрийский биолог – теоретик, с 1949г. живший в США и Канаде. Его уравнение представляет рост как результат двух процессов: анаболизма (синтеза веществ) и катаболизма (распада веществ).

3. Уравнение логистической функции исходит из предположения, что скорость роста прямо пропорциональна весу животного в данный момент и разности предельного веса и веса в данный момент.

Перечисленные уравнения содержат трудно определимые константы и имеют скорее чисто теоретическое значение.

Из других теорий роста необходимо отметить следующие:

Физико-химическая теория роста (С. Броди, Т. Робертсон, В. Оствальд), которая основана на аналогии роста с кинетическими кривыми некоторых химических реакций.

Балансовая теория роста (Заика В. А.).

Основное положение этой теории состоит в следующем:

То, что остается в теле есть разность между тем, что в него попадает и тем, что его покидает.

Феноменологическая теория роста (Зотин А. И., Зотина Р. С.) основана на термодинамике необратимых процессов.

Большой вклад в теорию роста внес русский академик И. И. Шмальгаузен (1884 – 1963), выдающийся биолог своего времени, сочетавший в себе талант экспериментатора и теоретика, широко применявший в биологии математические методы.

Цель настоящей работы состоит в следующем:

Получить формулу роста многоклеточного организма, основываясь на его аналогии с популяцией клеток.

Следует отметить, что рассматривается только период, когда происходит увеличение массы организма, т.е. с начала роста до достижения организмов предельного размера.

Итак, будем рассматривать многоклеточный организм как популяцию синхронно делящихся клеток, т.е. наделяем все клетки многоклеточного организма одинаковым средним потенциалом роста.

Ясно, что, такое сравнение далеко от действительности. Ведь разные клетки делятся с разной скоростью, а иные вообще перестают делиться. И тем не менее, такая усредненная картина роста дает возможность обнаружить общую закономерность этого процесса.

Как известно, популяция одноклеточных организмов при наличии всех необходимых для роста условий, удваивает свою массу с одним и тем же периодом, т.е. растет по закону экспоненты:

(1)

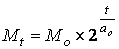
М _t – масса в момент времени t

а_о – период удвоения массы

Поставим задачу: распространить формулу (1) на многоклеточный организм. Нарастание массы многоклеточного организма происходит в основном за счет роста и деления клеток.

Общеизвестный факт – рост многоклеточного организма замедляется с течением времени. Хотя рост живого имеет колебательный характер, а именно за подъемами роста следует торможение, за которыми вновь следуют подъемы, сменяющиеся периодами депрессии, но общая тенденция роста многоклеточного организма – неуклонное падение скорости с течением времени.

По этой причине формула (1) в применении к многоклеточному организму примет вид:

(2)

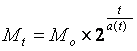
где а( t ) – неизвестная нам пока функция времени.

Для определения вида этой функции обратимся к экспериментальным данным по росту. Имея экспериментальную табличную зависимость М= f ( t ), вычисляем для каждого момента времени t соответствующее значение а по формуле:

и строим график а= f ( t ).

Анализ экспериментальных данных свидетельствует о том, что для всех живых организмов, как в эмбриональном, так и в постэмбриональном периоде, как для целых организмов, так и для отдельных органов и тканей, как для животных, так и растений период удвоения массы нарастает по линейному закону:

где a_o — начальный период удвоения массы

к – коэффициент замедления роста

Формула (3) применима также и для роста одноклеточных организмов, если рассматривать не рост популяций, а рост отдельных особей.

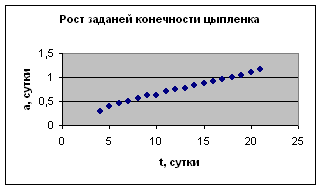
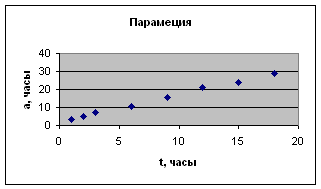
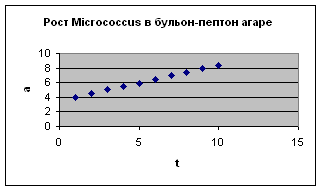
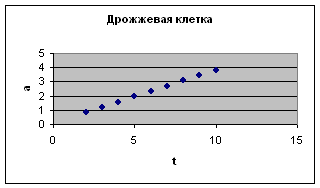
Это наглядно видно на примере одноклеточных – парамеции, дрожжевой клетки и mi с rococ c us (экспериментальные данные И.И. Шмальгаузена и Е. Сингаевской). Отсюда следует вывод о том, что замедление роста имеет место уже на уровне одной клетки.

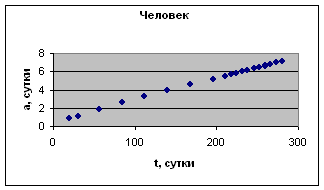
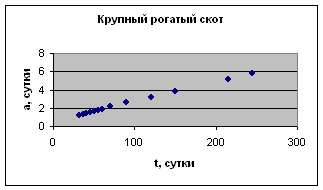
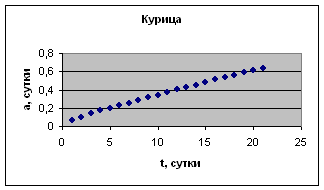
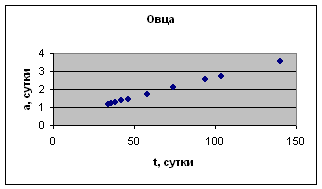
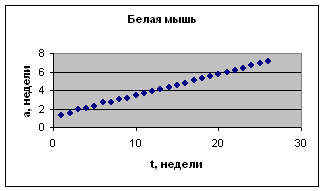
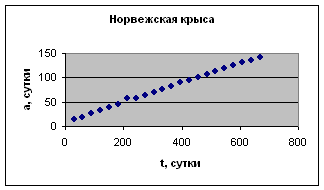
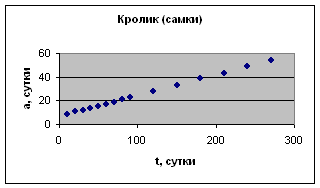
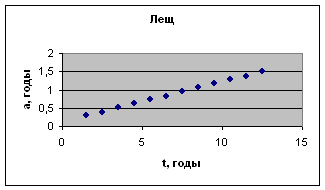
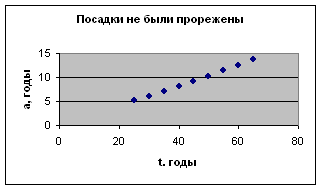
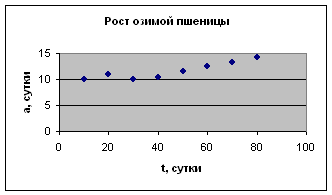
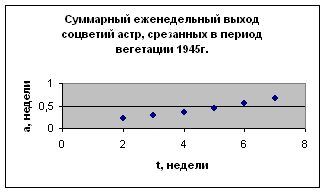
На рис. 1 приведены примеры зависимости а( t ) для отдельных организмов.

за М ₀ принята масса зиготы 5•10 -9 г

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.1, с.75

Экспериментальные данные взяты из книги К.Б. Свечина и др. «Возрастная физиология животных» с.33

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.1, с.144

Экспериментальные данные взяты из книги К.Б. Свечина и др. «Возрастная физиология животных» с.33

Постэмбриональный рост

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.2, с.163

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.2, с.165

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.1, с.167

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.2, с.133

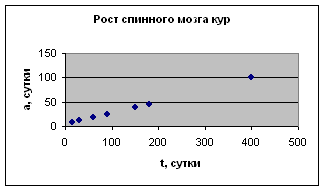
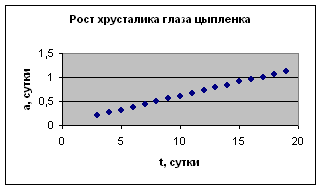
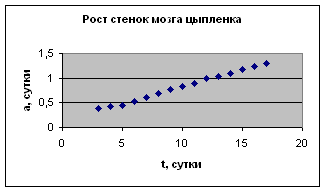
Рост отдельных органов и тканей животных

Экспериментальные данные взяты из сборника статей «Актуальные проблемы ветеринарной и зоотехнической науки в интенсификации животноводства», с. 157

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.1, с.31

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.1, с.31

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.1, с.78

Рост одноклеточных

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.2, с.38

t , а – интервалы по 6 минут

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.2, с.115

t , а – интервалы по 6 минут

Экспериментальные данные взяты из книги И.И. Шмальгаузена «Рост и дифференцировка» т.2, с.37

Рост растений

Ель ситхинская, 12-й класс бонитета.

Бонитет- показатель продуктивности леса. Зависит от почвы, климата и других условий.

Экспериментальные данные взяты из книги М.Р.В. Уиллиамса «Рациональное использование лесных ресурсов», с. 99

Экспериментальные данные взяты из журнала «Сельскохозяйственная биология». 1990, №5, с. 73

Экспериментальные данные взяты из книги Л. Бартона «Хранение семян и их долговечность», с. 188

Подставив значение а( t ) = а ₀ + к t в формулу (2), получим значение массы биологического объекта в момент времени t :

(4)

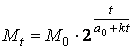
Следует отметить, что формула (4) применима только для нормальных условий роста организма. Она не учитывает вариации роста, связанные с изменением питания, индивидуальными особенностями организма, с сезонными изменениями роста и т. п. Данная формула даёт усреднённую картину роста, выявляя общую закономерность этого процесса. Универсальность формулы (4) даёт основание полагать, что в основе замедления роста всех живых организмов лежит единая причина. С количественной точки зрения всё многообразие животного и растительного мира сводится к различию двух параметров а ₀ и к.

Можно предположить, что увеличение периода удвоения массы а( t ) продолжается и после достижения организмом предельного размера. При некотором значении t период a ( t ) становится на столько большим, что становится невозможной физиологическая регенерация, т. е. организм не в состоянии возместить отмирающие клетки. Это и определяет биологический предел жизни организма.

Частные случаи формулы (4) при k = 0

1) Рост популяции одноклеточных организмов.

При k = 0 формула (4) принимает вид (1).

Не6обходимо подчеркнуть, что сама популяция одноклеточных при наличии всех необходимых для роста условий растёт без замедления, удваивая свою массу через постоянное время, а каждая особь этой популяции растёт с замедлением т. е. по формуле (4).

2) Злокачественный рост в начальной стадии.

Внедрение кинетики в онкологию связано с работами академика Н. М. Эмануэля. В его труде «Кинетика экспериментальных опухолевых процессов» приведены результаты, полученные разными исследователями по росту большого количества злокачественных опухолей.

Из этих результатов Н. М. Эмануэль делает вывод о том, что рост злокачественных опухолей в начальный период своего развития выражается экспоненциальной ф-ей :

,

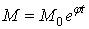
где j – постоянная величина.

Эта формула может быть приведена к виду формулы (1).

Следовательно, злокачественная опухоль в начальной стадии растет без замедления роста также как и популяция одноклеточных организмов.

По мере роста опухоли экспоненциональный характер роста нарушается. Это связано с разными причинами, в т. ч. потерей клеток опухолью, нарушением питания центральной части опухоли и пр.

При некоторых опухолях экспоненциональный характер роста сохраняется вплоть до гибели животного.

Из формулы (4) вытекают 2 следствия.

Формула позволяет приблизительно, пусть и с небольшой точностью оценить верхний предел роста организма.

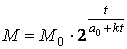
При t ®Ґ

След .,

Величина 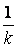близка к пределу Хейфлика.

Т. о., предельный размер любого организма определяется одним параметром – коэффициентом замедления его роста.

Если задать вопрос – почему мышь при самом обильном питании и самых благоприятных условиях никогда не вырастет до размеров кошки, и наоборот, рост кошки при самом голодном рационе никогда не остановится на размере мыши, то ответ будет таков – потому, что у мыши коэффициент замедления роста К больше, чем у кошки.

Параметр a ₀ определяет время, в течение которого организм достигает своего предельного размера, а последнее, в большинстве случаев связано прямой зависимостью с продолжительностью жизни организма.

Ясно, что формула роста (4) не может дать ответ на вопрос – в чём материально выражены параметры – a ₀ и k . Для этого необходимы целенаправленно поставленные эксперименты и их осмысление.

ЛИТЕРАТУРА

1. Бартон Л. Хранение семян и их долговечность. – М.: Колос, 1964. – 240 с. [Пер. с англ.].

2. Свечин К. Б., Оршавский И. А. и др. Возрастная физиология животных. – М.: Колос, 1967. – 431 с .

3. Уиллиамс М. Р. В. Рациональное использование лесных ресурсов. – М.: Экология, 1991 – 124 с. [Пер. с англ.].

4. Федюшин А. А. и др. КПД ФАР Озимой пшеницы как фактор программирования её продуктивности // Сельскохозяйственная биология. – М.: 1990. — №5. – C. 70-75.

5. Хрусталёва И. В., Фань Гуанли. Возрастные изменения морфологии спинного мозга кур . п ри клеточном содержании // Актуальные проблемы ветеринарной зоотехнической науки в интенсификации животноводства. – М. 1990. – C. 156 – 157.

6. Шмальгаузен И. И. Рост и дифференцировка, т. 1. – Киев: Наукова думка,1984. – 176 с .

7. Шмальгаузен И. И. Рост и дифференцировка, т. 2. – Киев: Наукова думка, 1984. – 168 с .

8. Эмануэль Н. М. Кинетика экспериментальных опухолевых процессов. М.: Наука,1977. – 416 с .

Поступила в редакцию 10.12.2003.

Growth vegularity of biological objects

Experimental data analysis of living organisms’ growth proves that the growth of all forms of life accommodates it self to the rule given in simple formula, containing two parameteres, so the difference between them, from – quantitative point of view, explains all the diversification of animal and vegetable world.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ РОСТА БЕРТАЛАНФИ ПРИ ОТСУТСТВИИ РЕГУЛЯРНЫХ ИЗМЕРЕНИЙ

Институт биологии южных морей НАН Украины, г. Севастополь e-mail: vfjuck@mail.ru

Количественным показателем развития рыб является их рост. Поэтому математическая оценка количественных параметров роста в естественных условиях имеет первостепенное значение при изуче­нии динамики рыбных ресурсов и разработке мероприятий по их рациональному использованию.

Для количественной оценки параметров роста рыб чаще всего используют уравнение линей­ного роста Берталанфи (Bertalanffy L., 1964; РикерУ., 1979):

где l(t) — длина рыбы в момент времени t;

L — средняя предельная длины рыбы исследуемой популяции;

K — константа, характеризующая скорость изменения длины;

t0 — константа, указывающая момент времени, в который длины рыбы в принятой модели рос­та (1) была равна нулю;

(t — t0) — время, прошедшее от рождения рыбы (возраст рыбы).

Уравнение (1) позволяет для заданного возраста рыбы определить ее длину или прирост дли­ны за фиксированный отрезок времени (год, сезон и т.д.), оно используется для нахождения инди­видуального и популяционного роста особей промыслового стада, расчете продукционных характе­ристик и т.д.

В уравнении (1) содержится три неизвестных коэффициента L, K и t0, которые должны быть определены на основе экспериментальных измерений. Существуют разные методы нахождения этих коэффициентов (Hohendorf K.; 1966, Рикер У.Е., 1979; Барыбина А.И., 1978 и др.). Однако не­достатком всех этих методов является то, что для определения неизвестных коэффициентов длина рыбы должна быть известна через равные интервалы времени. Если интервалы времени, для кото­рых определена длина, не являются постоянными (то есть отсутствуют регулярные измерения), то для этих случаев известные методы не применимы.

Целью данной работы является разработка методики определения коэффициентов уравнения линейного роста Берталанфи на основе экспериментальных измерений длины, проведенных через неравные интервалы времени.

Если продифференцировать уравнение (1) и провести несложные преобразования, то можно получить следующее выражени

— скорость роста рыбы.

Из уравнения (1) видно, что скорость роста зависит от длины рыбы. Анализ показывает, что выражение (2) является уравнением линейной функции в декартовой системе координат, по оси абсцисс которой откладывают длину рыбы l(t) в некоторый момент времени t, а по оси ординат ско-

рость роста рыбы в этот момент. В момент времени tk, когда длина рыбы достигнет пре­дельной длин скорость ее роста становится равной нулю. И н нт времени

t0, когда длина рыбы равна нулю, скорость ее роста максимальна и равна Это можно

использовать для нахождения неизвестных коэффициентов уравнения Берталанфи.

На рис. 1 изображены и отмечены кружками значения скорости роста рыбы в зависимости от

длины, найденные на основе измерений длины в некоторые моменты времени t. В соответствии с выражением (2) значения скорости роста, могут быть аппроксимированы прямой линией, проходя­щей через эти точки. Аналитическое выражение этой прямой, позволяет найти неизвестные коэф­фициенты уравнений (2) и (1).

Рис. 1. Зависимость скорости роста рыбы от длины

1 — Значения скорости роста, найденные на основе измерений длины и возраста; 2 — Линейная зависимость в соответст­вии с уравнением (2)

В соответствии с изложенным выше, определение коэффициентов уравнения роста Берталан- фи можно проводить в следующей последовательности.

2). Затем для нескольких последовательных пар значений изменения возраста находят сред­нею длину пиби на /-пм интервале изменения возраста

б). Находим коэффициент t0 как среднее всех значений, рассчитанных по формуле (4).

Таким обпазом, ппедлагаемая методика позволяет достаточно ппосто пассчитать коэффициен- ти упавнения поста Бепталанфи по измепенним значениям длини пиби и ее возпасте. Достоинст­вом методики является то, что измепения длини не обязательно должни ппоизводиться чепез пав- ние интепвали впемени.

Барыбина А. И., 1978. Некоторые способы определения параметров уравнений роста Берталанфи // Применение математических способов оценки состояния промысловых объектов мирового океана: Тр. ВНИРО. Т. CXXVIII. С. 67 — 71.

Рикер У. Е., 1979. Методы оценки и интерпретации биологических показателей популяций рыб. М.: Пищ. пром-сть. 408 с.

Bertalanffy L., 1964. Basic concepts in quantitative biology of metabolism // Helgolander Wissenschaftliche Meeresuntersuchungen. V. 9. № 1 — 4. P. 5 — 37.

Hohendorf K., 1966. Eine Diskussion der Bertalanffy — Funktionen und ihre Anwendung zur Charakterisierung des Wachstums von Fischen // Kieler Meeresforshungen. V. XXII. № 1. P. 70 — 97.

DEFINITION OF COEFFICIENTS OF THE BERTALANFFY GROWTH EQUATION WHEN REGULAR MEASUREMENTS ARE LACKING

Institute of biology of the southern seas of NAS of Ukraine, Sevastopol, Ukraine e-mail: vfjuck@mail.ru

Transformation of Bertalanffy linear growth equation has been conducted and dependence of fish growth rate on its length has been found. On the base of the expression obtain ell and also experimental measurement of length and age of fish, the method of calculation of coefficients of the Bertalanffy growth equation is has been developed. The amount of measurements must be no less than three. With increase of amount of measurements due to the statistical data processing the error of definition of coefficients of growth equation diminishes. Fish length measurements can be carried out in unequal time intervals and this is an advantage of the methodic developed. It allows to find the parameters of individual and population grows of the food fish shoal when regular measurements are lacking.