Уравнение биссектрисы в треугольнике — формула, свойства и решение задач
Треугольник является одной из самых простых фигур, которая часто встречается школьникам в задачах по геометрии. В свою очередь, биссектриса представляет собой важный элемент, характеризующий тот или иной угол. Решение геометрических проблем с участием этих объектов требует наличия определенных знаний. Чтобы уметь составлять по координатам вершин уравнение биссектрисы треугольника, необходимо понимать выражения для прямых линий.
Прямая на плоскости
Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:
Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:
Делящая пополам угол линия
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.
Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.
Способы построения
В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:
Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.
В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.
Основные свойства
Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.
Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.
Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.
В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:
Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.
Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:
Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.
Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.
Уравнение биссектрисы треугольника
Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.
В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):
Пример решения задачи
Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.
Сначала нужно написать уравнения прямых для сторон AB и CB, получается:
- AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
- CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.
Составить уравнения биссектрис можно так:
| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.
Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:
Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:
Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:
При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:
- D1A = 1,4; D1C = 3,635;
- D2A = 0,621; D2C = 1,614.
Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:
BD2 = 2,014 единицы.
Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.
Образцы выполнения некоторых заданий
Рассмотрим решения некоторых практических упражнений.
Задание 2(е)
На плоскости даны точки А(11; -5), В(6;7), С(-10; -5). Найти уравнение биссектрисы угла А.
Решение задания 2(е)
Найдем направляющий вектор 


или (умножая на 






Таким образом, в качестве направляющего вектора биссектрисы угла А можно взять вектор 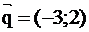

Задание 3
Дана точка (0;2) пересечения медиан треугольника и уравнения двух его сторон 5х – 4у + 15 = 0 и 4х + у – 9 = 0. Найти координаты вершин треугольника и уравнение третьей стороны.
Решение Координаты одной вершины найдем как координаты точки пересечения данных сторон, для чего решим систему уравнений
Получаем 
Точка Оц пересечения медиан треугольника называется его центром. Отметим одно свойство центра треугольника, которое используем для нахождения координат остальных вершин:


где хц, уц – координаты центра треугольника;
хi, yi – координаты i-ой вершины треугольника,
Для доказательства этих формул рассмотрим треугольник А1А2А3, где Аi(xi;yi), i = 1-3 (см.рис.2.1).
Рис.2.1. Вспомогательный чертеж к заданию 3
Пусть В середина стороны А1А2. Тогда А3В – медиана треугольника А1А2А3. По известному из элементарной геометрии свойству медиан треугольника 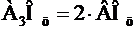
Тогда координаты точки В найдем по формулам


а координаты центра Оц из векторного соотношения 


Отсюда, выражая хц и уц через xi, yi, получим требуемые формулы.
Вернемся к решению задания 3. Используя доказанные формулы, полагая в них х1 = 1 и у1 = 5, хц = 0 и уц = 2, получим два уравнения, которым должны удовлетворять координаты остальных двух вершин

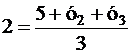
Еще два уравнения получим, если потребуем, чтобы искомые точки, вершины треугольника, принадлежали заданным сторонам, т.е. их координаты удовлетворяли уравнениям этих сторон
Итак, для определения четырех неизвестных х2, у2, х3, у3, мы имеем четыре независимых (!) условия (уравнения)
Решив эту систему, получим х2 = -3, у2 = 0, х2= 2, у3 = 1.
Наконец, уравнение третьей стороны запишем как уравнение прямой, проходящей через две заданные точки (-3;0) и (2;1)


Итак, уравнение третьей стороны x – 5у + 3 = 0, а вершины треугольника имеют координаты (1;5), (-3;0), (2;1).
Задание 7
Составить уравнение линии, для каждой точки М которой, отношение расстояний до точки F( 

равно 
Привести уравнение линии к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).
Замечание. Отметим, что в заданиях этого модуля 
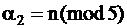

Пусть n = 101. Тогда:






Итак, для n = 101 первая часть задания 7 принимает вид:
Составить уравнение линии, для каждой точки М которой, отношение расстояния до точки F(-4;1) и до прямой x = 1
равно 
Решение задания 7 (для n = 101).
Пусть М(х;у) произвольная точка искомой линии, r – расстояние от М до F и d – расстояние от точки М до прямой x = 1. Тогда


По условию 

Упростим уравнение линии и приведем его к каноническому виду. Для этого возведем обе части уравнения в квадрат и выполним следующие преобразования уравнения
х 2 – 2х +1 = 4х 2 + 32х + 64 + 4(у – 1) 2 ,
3х 2 + 34х + 4(у – 1) 2 + 63 = 0,


Последнее уравнение – это каноническое уравнение эллипса с полуосями 








Рис.2.2. Эллипс с уравнением
Фокусы эллипса имеют координаты 


Итак, координаты фокусов F1(-4;1), F2( 
Директрисы эллипса имеют уравнения 

Уравнения директрис 
D2: 
Отметим фокусы и директрисы эллипса на рис.2.2.
Обратите внимание на совпадение фокуса F1 с точкой, данной в условии задания 7, на совпадение директрисы D1 с прямой х = 1 из условия этого задания, и совпадение эксцентриситета е с параметром е в условии. По этому поводу см. теоретическое упражнение 18.
В пространстве даны точки А(-2; -4;1), В(3;1; -1), С(5;1;1),
S(1;-4;0). Найти координаты центра и радиус вписанной в пирамиду SABC сферы (условие сформулировано для n = 101).
Решение задания 4(м)
Пусть точка О(x0;y0;z0) – центр сферы, вписанной в пирамиду SABC. Найдем точку О как точку, равноудаленную от граней пирамиды. Для этого найдем уравнения всех граней и расстояния от точки О до этих граней (уравнения некоторых граней находятся в предшествующих пункту М пунктах задания 4).
Грань АВС. Уравнение грани

Точки О и S лежат по одну сторону от грани АВС, поэтому отклонения этих точек от грани АВС имеют одинаковые знаки. Отклонение 


Аналогично все делается для граней ABS, BCS, CAS.
Грань ABS имеет уравнение 5х + у + 15z – 1 = 0 и

Грань BCS имеет уравнение 5х – 3у – 5z – 17 = 0 и
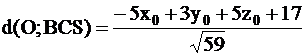
Наконец, грань CAS имеет уравнение 5х – 7у + 15z + 33 = 0 и

Так как О – центр сферы, вписанной в пирамиду SABC, то
d(O; ABC) = d(O; ABS) = d(O; BCS) = d(O; CAS) = r,
где r – радиус вписанной сферы.
Тогда координаты точки О должны удовлетворять системе

и уравнение вписанной сферы

1. Общее уравнение прямой на плоскости. Нормальный вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.
2. Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности.
3. Каноническое и параметрическое уравнения прямой на плоскости. Направляющий вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.
4. Уравнение прямой, проходящей через две заданные точки.
5. Уравнения прямых, проходящих через данную точку параллельно и перпендикулярно данной прямой (3 случая задания данной прямой: общим уравнением, каноническим уравнением, уравнением с угловым коэффициентом).
6. Общее уравнение плоскости в пространстве, нормальный вектор плоскости. Угол между плоскостями. Условие параллельности и перпендикулярности.
7. Уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой.
8. Общее, каноническое и параметрическое уравнения прямой в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности.
9. Угол между прямой и плоскостью в пространстве. Условие параллельности и перпендикулярности прямой и плоскости.
10. Уравнение плоскости, проходящей через данную точку, перпендикулярно данной прямой. Уравнение прямой, проходящей через данную точку, перпендикулярно данной плоскости.
11. Расстояние от точки до: прямой на плоскости; прямой в пространстве; плоскости в пространстве.
12. Уравнение линии на плоскости. Общее уравнение кривой второго порядка.
13. Каноническое и параметрическое уравнения окружности.
14. Эллипс (фокусы и директрисы, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения эллипса.
15. Гипербола (фокусы, директрисы и асимптоты, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения гиперболы.
16. Парабола (фокус и директриса, фокальный радиус точки, эксцентриситет). Каноническое уравнение параболы.
17. Приведение общего уравнения кривой второго порядка к каноническому виду.
18. Полярные координаты на плоскости. Уравнение линии в полярных координатах.
19. Уравнение поверхности в пространстве. Общее уравнение поверхностей второго порядка.
20. Основные типы поверхностей второго порядка и их канонические уравнения.
1. Бугров Н.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980. 176 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1: Учебное пособие для студентов втузов. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1980. 320 с.
3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1981. 232 с.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980. 240 с.
5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа/Под ред. А.В. Ефимова, Б.П. Демидович. – М.: Наука, 1981, 464 с.
6. Высшая математика. Методические указания и контрольные задания/Под ред. Ю.С. Арутюнова. – М.: Высшая школа, 1985.
7. Гусак А.А. Пособие к решению задач по высшей математике. – Изд. 3-е. – Минск: Изд-во БГУ, 1973. 532 с.
8. Кузнецов А.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов. – М.: Высшая школа, 1983. 175 с.
9. Погорелов А.В.Аналитическая геометрия.– М.:Наука, 1968. 176с
Уравнение биссектрисы треугольника по координатам вершин – формула
Биссектриса треугольника
Напомним, что биссектрисой угла называют луч, делящий угол пополам.
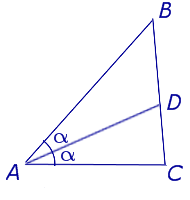
Определение . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника и соединяющий вершину треугольника с точкой на противоположной стороне (рис 1).
Поскольку в каждом треугольнике имеются три угла, то в каждом треугольнике можно провести три биссектрисы.
На рисунке 1 биссектрисой является отрезок AD .
Теорема 1 . Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
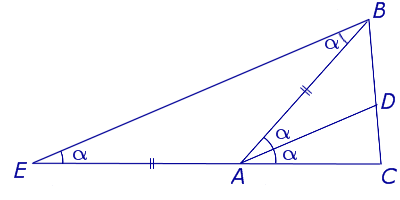
Доказательство . Продолжим сторону AC треугольника ABC , изображенного на рисунке 1, за точку A . Проведем через точку B прямую, параллельную биссектрисе AD . Обозначим точку пересечения построенных прямых буквой E (рис. 2).
Докажем, что отрезки AB и AE равны. Для этого заметим, что угол EBA равен углу BAD , поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD . Заметим также, что угол BEA равен углу DAC , поскольку эти углы являются соответственными при параллельных прямых EB и AD . Таким образом, угол EBA равен углу BEA , откуда вытекает, что треугольник EAB является равнобедренным, и отрезки AB и AE равны.
Отсюда, воспользовавшись теоремой Фалеса, получаем:
что и требовалось доказать.
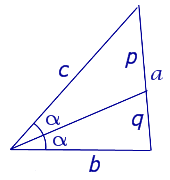
Следствие 1 . Рассмотрим рисунок 3, на котором изображен тот же треугольник, как и на рисунке 1, но для длин отрезков использованы обозначения
b = |AC|, a = |BC|, c = |AB|, p = |BD|, q = |DC|.
что и требовалось доказать.
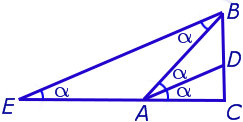
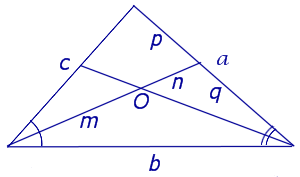
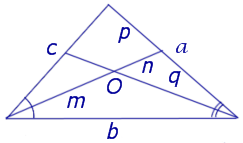
Следствие 2 . Рассмотрим рисунок 4, на котором изображены две биссектрисы треугольника, пересекающиеся в точке O .
Тогда справедлива формула:
что и требовалось доказать.
Теорема 2 . Рассмотрим рисунок 5, который практически совпадает с рисунком 2.
Тогда для длины биссектрисы справедлива формула:
Доказательство . Из рисунка 5 следует формула
Если воспользоваться этой формулой, то из подобия треугольников ADC и EBC , получаем:
что и требовалось доказать.
Теорема 3 . Длину биссектрисы треугольника (рис.6) можно найти по формуле:
Доказательство . Рассмотрим рисунок 6
откуда с помощью Теоремы 2 получаем:
что и требовалось доказать.
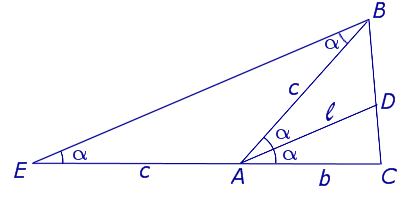
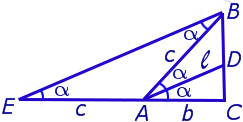
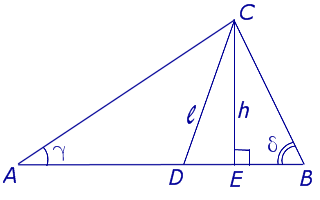
Задача . Из вершины C треугольника ABC (рис.7) проведена биссектриса CD и высота CE .
Доказать, что выполнено равенство:
Решение . Поскольку CD – биссектриса угла ACB , то
Поскольку CE – высота, то
что и требовалось доказать.
Из решения этой задачи вытекает простое следствие.
Следствие . Длины биссектрисы CD и высоты CE связаны следующей формулой:
Биссектриса треугольника онлайн
С помощю этого онлайн калькулятора можно найти биссектрису треугольника. Для нахождения длины биссектрисы треугольника введите длины сторон треугольника, выберите сторону, к которой проведена биссектриса и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Определение 1. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны называется биссектрисой треугольника (Рис.1).
 |
Биссектриса треугольника также называют биссектрисей угла треугольника или биссектрисей внутреннего угла треугольника.
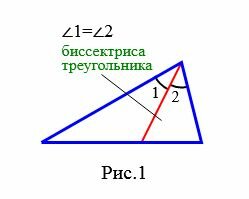
Биссектриса внешнего угла треугольника − это биссектриса угла, которая является смежным с внутренним углом треугольника (Рис.2).
 |
Любой треугольник имеет три биссектрисы.
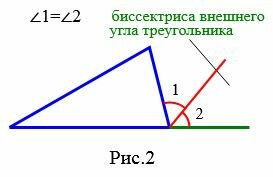
Теорема 1. Биссектрисы треугольника пересекаются в одной точке.
 |
Доказательство. Проведем биссектрисы AA1, BB1 и обозначим через O точку их пересечения (Рис.3). Из точки O проведем перпендикуляры OK, OM и OL по сторонам треугольника ABC. По теореме 1 статьи Биссектриса угла. Свойства − OK=OL OK=OM. Следовательно OL=OM. Но последнее равенство означает, что точка O равноудалена от сторон AC и BC, т.е. находится на биссектрисе CC1 (Определение 2 статьи Биссектриса угла. Свойства).
Точка пересечения биссектрис треугольника называется инцентром треугольника. Инцентр треугольника является центром вписанной в треугольник окружности (Рис.4).
 |
Доказательство следует из теоремы 1, поскольку точка O равноудалена от сторон треугольника ABC и, следовательно, является центром окружности равной OK=OL=OM.
Длина биссектрисы треугольника
Рассмотрим треугольник на Рис.5.
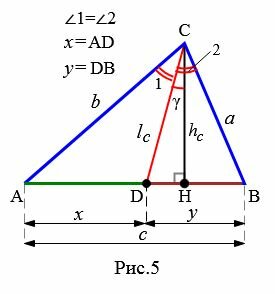 |
Длина биссектрисы треугольника можно вычислить следующими формулами:
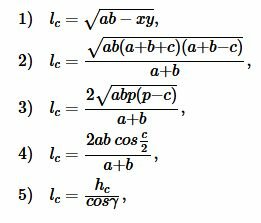 |
где p − полупериметр треугольника ABC, ( small gamma -) угол между биссектрисой ( small l_c) и вершиной ( small h_c:)
 , , 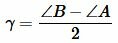 |
Доказательство. 1) Из теоремы Стюарта следует:
 | (1) |
А из теоремы о биссектрисе треугольника следует, что если lc является биссектрисей треугольника ABC (Рис.5), то имеет место следующее соотношение:
 | (2) |
Поскольку 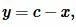
 | (3) |
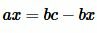 |
 | (4) |
 |
 | (5) |
Подставим (4) и (5) в (1):
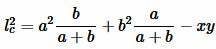  |
 . . | (6) |
 . . |
Доказательство. 2) Подставим (4) и (5) в (6):
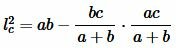 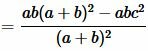 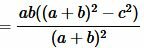 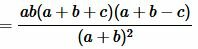 , , |
 . . | (7) |
 . . | (8) |
Доказательство. 3) Сделаем следующее обозначение:
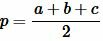 . . | (9) |
Сделаем преобразования формулы (7), учитывая (9):
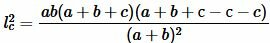 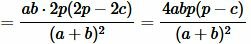 . . |
 . . | (10) |
Доказательство. 4) Для доказательства четвертой формулы, снова обратимся к рисунке Рис.5. Запишем формулы площадей треугольников ABC, ADC и BDC:
 , , |
 , , |
 . . |
Учитывая, что 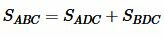
 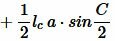 |
 . . |
 . . | (11) |
Для ( small sin C ) применим формулу синуса двойного угла:
 . . | (12) |
Подставляя (12) в (11) получим:
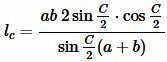 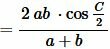 . . |
 . . | (13) |
Доказательство. 5) Докажем пятую формулу. Из вершины C проведена вершина CH. Имеем прямоугольный треугольник CHD, для которого имеет место следующее равенство:
 . . |
 . . |
Остается показать, что 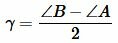
Поскольку биссектриса lc делит угол C пополам, то:
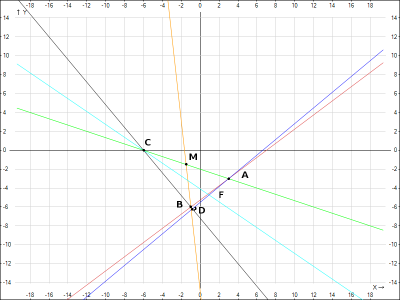
Решаем типовую задачу по аналитической геометрии. Прямая линия на плоскости.
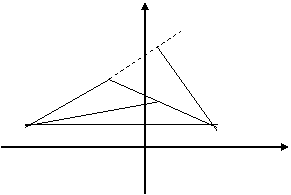
Рассмотрим принцип решения задач по теме : “Прямая линия на плоскости, нахождение уравнения прямой, проходящей через заданную точку, нахождение точек пересечения, углов биссектрис и т.д.”.
В качестве примера рассмотрим следующую задачу
Пример: Даны координаты вершин треугольника (ABC) (A(3; -3); B(-1;-6); C(-6;0))
=1,62)
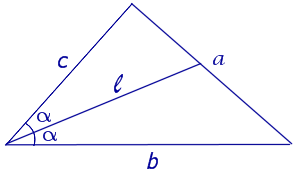
Определение и свойства биссектрисы угла треугольника
В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.
- Определение биссектрисы угла треугольника
- Свойства биссектрисы треугольника
- Свойство 1 (теорема о биссектрисе)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Пример задачи
Определение биссектрисы угла треугольника
Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.
Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.
Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.
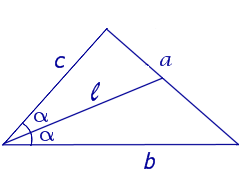
Внешней называется биссектриса угла, смежного с внутренним углом треугольника.
Свойства биссектрисы треугольника
Свойство 1 (теорема о биссектрисе)
Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):
Свойство 2
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.
Свойство 3
Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).
Свойство 4
Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):
BD 2 = AB ⋅ BC – AD ⋅ DC
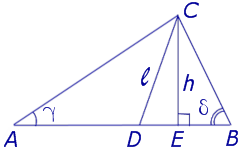
Свойство 5
Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.
- CD – внутренняя биссектриса ∠ACB;
- CE – биссектриса угла, смежного с ∠ACB;
- ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.
Пример задачи
Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.
Решение
Нарисуем чертеж согласно условиям задачи.
Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.
Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):
Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29
Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.
Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.
Уравнение биссектрисы треугольника по координатам вершин – формула
| Учебный курс | Решаем задачи по геометрии |





















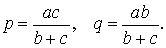
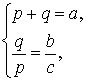
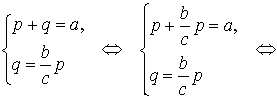
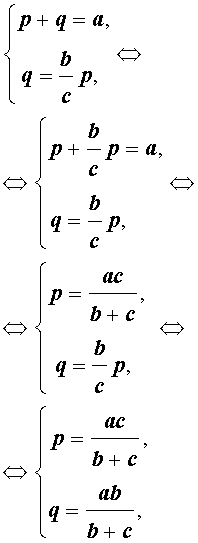
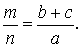
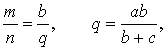
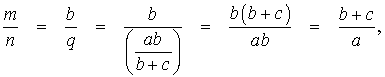
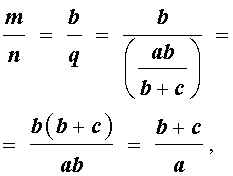
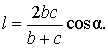
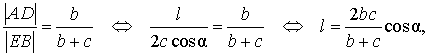
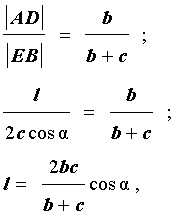
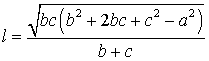
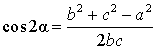
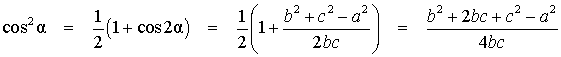
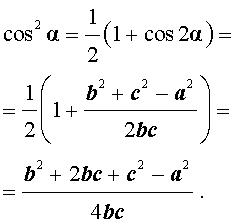
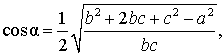
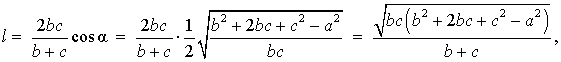
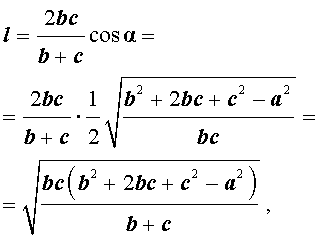
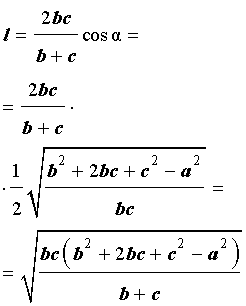
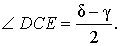
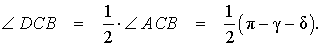
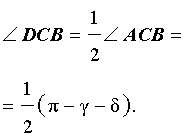
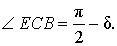
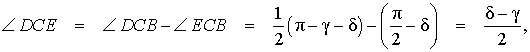
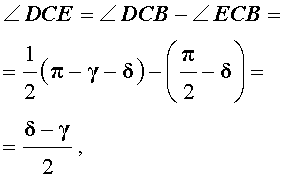
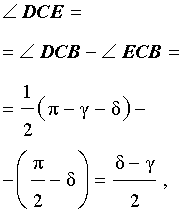






















 Y
Y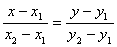 .
.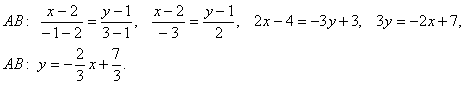
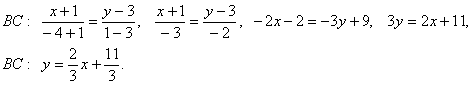
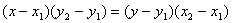 .
.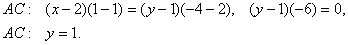
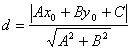 .
.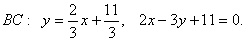
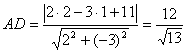 .
.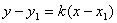 .
.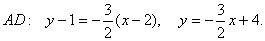
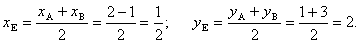 Точка Е (1 /2,2).
Точка Е (1 /2,2).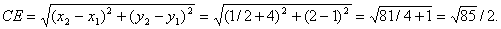
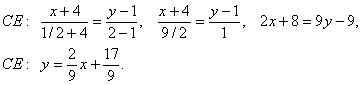
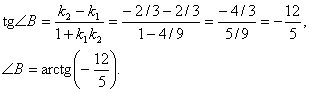
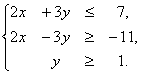
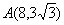 .
.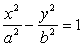 . Так как гипербола проходит через точку А (8;
. Так как гипербола проходит через точку А (8; 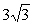 ), то ее координаты удовлетворяют уравнению гиперболы, т.е.
), то ее координаты удовлетворяют уравнению гиперболы, т.е. 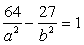 . Так, как
. Так, как 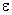 = 1,25, то
= 1,25, то 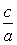 = 1,25, но
= 1,25, но 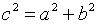 , тогда
, тогда 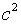 = 1,5625
= 1,5625 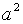 или
или 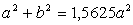 .
.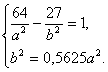
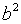 = 9, следовательно, каноническое уравнение гиперболы имеет вид
= 9, следовательно, каноническое уравнение гиперболы имеет вид 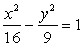 .
. и центр окружности
и центр окружности 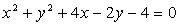 .
.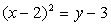 ;
;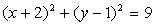 .
.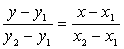 .
.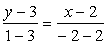 , или
, или 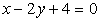 .
.