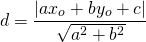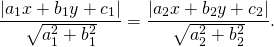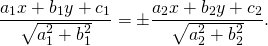Уравнение биссектрисы угла по точке и прямой

Уравнение биссектрисы угла

Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.

Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0.

Расстояние от точки (x_o;y_o) до прямой ax+by+c=0 определяется по формуле

По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.

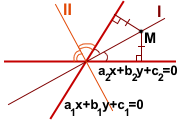
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0, находится от этих прямых на одинаковом расстоянии, то есть

Это равенство можно записать в виде

Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.

Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.

В формулу уравнения биссектрис подставляем данные прямых:

Задача 34288 Составить уравнение биссектрисы угла.

Условие

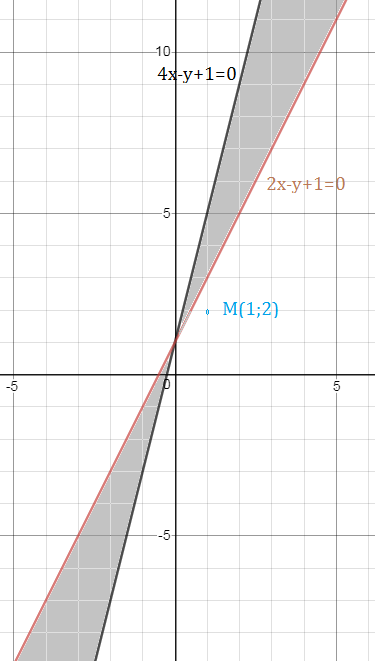
Составить уравнение биссектрисы угла между прямыми l1(4x–y+1=0) и l2(2x–y+1=0) смежного с углом, содержащим точку M(1;2)

Решение

Пусть точка Р(х;у) лежит на биссектрисе угла между прямыми.
Это значит, что расстояние d_(1) это точки до прямой l_(1) равно
расстоянию d_(2) это точки до прямой l_(2)

Прямая 4x–y+1=0 разбивает плоскость хОу на две области:
4x–y+1>0 или 4x–y+1 0 — верно;
Прямая 2x–y+1=0 разбивает плоскость хОу на две области:
2x–y+1>0 или 2x–y+1 0 — верно;

Значит точка M принадлежит области
4x–y+1>0
2x–y+1>0
а смежные области задаются неравенствами противоположных знаков.

Поэтому в (#) знак модуля раскрывается так:
(4x-y+1)/sqrt(4^2+1^2) =- (2x-y+1)/sqrt(2^2+1^2)

Делим на (sqrt(5)+sqrt(17))

((2sqrt(17)+4sqrt(5))/(sqrt(17)+sqrt(5))) * x — y + 1=0

Избавляемся от иррациональности в знаменателе

[b]((7 — sqrt(85))/6)*x — y + 1 = 0[/b]

Свойство биссектрисы угла

Что такое биссектриса угла

Биссектриса угла — это луч с началом в вершине угла, который делит данный угол на два равных угла.

В О — биссектриса ∠ А В С , ∠ С В О = ∠ О В А .

Что такое биссектриса треугольника

Биссектриса треугольника — отрезок биссектрисы угла от вершины угла до пересечения с противоположной стороной треугольника.

Основание биссектрисы — точка пересечения биссектрисы с противоположной стороной.

A D — биссектриса ∠ С А В к стороне С В в Δ С А В . Точка D — основание биссектрисы A D .

Внешняя биссектриса — биссектриса внешнего угла треугольника.

∠ M N L смежный с ∠ M N K . N E — внешняя биссектриса Δ M N K , проведенная из вершины N .

Основное свойство биссектрисы угла

Биссектриса при вершине треугольника делит противоположную сторону на два отрезка, пропорциональных сторонам треугольника, прилежащим к данным отрезкам.

Если в Δ А В С отрезок A D — биссектриса ∠ С А В , то C D C A = D B B A .

1. В Δ С А В проведем биссектрису А D . ∠ С А D = ∠ D А В = ∠ α .
2. Проведем высоту А Н к стороне А В и найдем площади Δ С А D и Δ В А D .
3. S Δ С А D = 0 , 5 · А Н · D C .
4. S Δ B А D = 0 , 5 · А Н · D B .
5. S Δ С А D S Δ B А D = 0 , 5 · А Н · D C 0 , 5 · А Н · D B .
6. S Δ С А D S Δ B А D = D C D B .
7. Площади Δ С А D и Δ В А D также равны S Δ С А D = 0 , 5 · A D · A C · s i n α , S Δ В А D = 0 , 5 · A D · A В · s i n α .
8. S Δ С А D S Δ B А D = 0 , 5 · A D · A C · sin α 0 , 5 · A D · A В · sin α .
9. S Δ С А D S Δ B А D = A C A В .
10. Из пунктов 6 и 9 следует, что D C D B = A C A В . Теорема доказана.

Свойства биссектрис в треугольнике

1. В любом треугольнике можно провести три биссектрисы. Все они пересекаются в одной точке.
2. Точка пересечения биссектрис является центром окружности, вписанной в треугольник.
3. Точка пересечения делит биссектрисы в отношении, равном отношению суммы сторон, прилежащих к углу, к противоположной стороне.
4. В правильном треугольнике биссектриса является одновременно высотой и медианой.
5. Внутренняя и внешняя биссектрисы, проведенные из одного угла, перпендикулярны.

Пример решения задачи

Дано: биссектриса из ∠ D треугольника D E F делит противолежащую сторону E F на отрезки E K = 16 с м и K F = 36 с м , сторона D E равна 24 с м .

Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, которые соотносятся между собой так же, как прилегающие к ним стороны. Поэтому E K K F = D E D F . Составим уравнение, где D F = х :