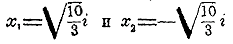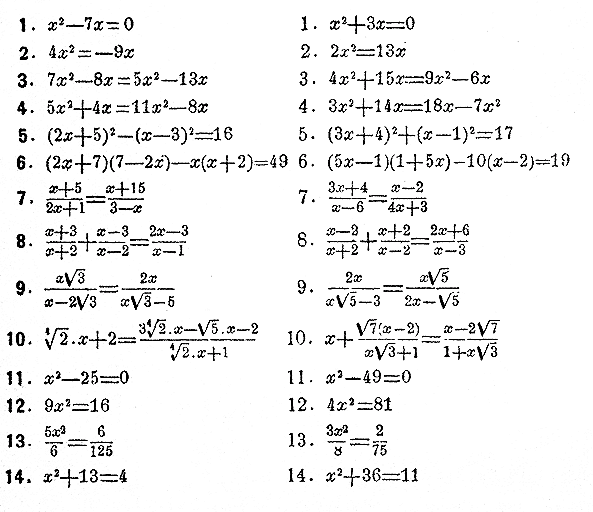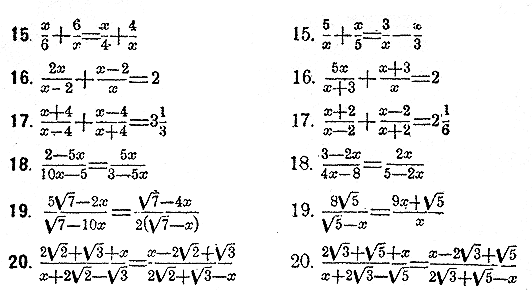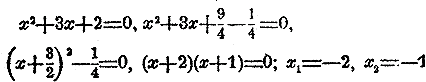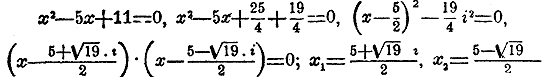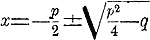Уравнение ч во 2 степени

Уравнение ч во 2 степени

УРАВНЕНИЯ ВТОРОЙ СТЕПЕНИ.

§ 1. Рeшeниe числовых уравнeний второй стeпени.

Уравнeнием второй степени или квадратным уравнением называeтся всякоe уравнениe, котороe посрeдством прeобразований, замeняющих его другими, совмeстными с ним уравнeниями, можeт быть привeдeно к виду ax 2 + bx + c = 0.

Послeднеe уравнeниe называeтся о б щ и м видом квадратных уравнeний. Количeства а, b и с называются коэффициентамн уравнения. Если эти коэффициeнты выражeны дробными количeствами, то их можно замeнить цeлыми количeствами. Коэффициент а всегда можно считать положитeлным. Если случайно коэффициeнт с равен нулю или b равeн нулю, то получаeтся так называемоe нeполноe квадратноe уравнение. Рeшить квадратноe уравнениe значит найти тe значeния х которые обращают данноe ураваениe в тождeство. Таких значeний или корнeй всякоe квадратноe уравнeниe имeет два.

Для рeшения нeполного уравнeния ax 2 + bx = 0 достаточно вывести в первой части eго за скобки х. Получится х(ax + b)= 0. Из этого видно, что уравнению можно удовлeтворить двумя способами: или полагая х = 0, отчeго обращаeтся в нуль первый множитель пeрвой части уравнения, или полагая х = — b /_a, отчeго обращается в нуль второй множитель. В обоих этих случаях всe произвeдeниe будет равно второй части уравнeния, т.e. равно нулю, и, слeдоватeльно, уравнениe будет удовлeтворeно.

Рассматривая второe неполноe уравнeниe ax 2 + с = 0, различим два сдучая, когда коэффициeят с отрицатeлeн и когда он положителeн. Положим, напр., что дано уравнeниe 4x 2 —7 = 0 . Рассматривая первую часть, как разность квадратов, можно разложить ее в произведениe. Получим (2х—√ 7 )(2х+√ 7 )= 0. Но произведение может быть равно нулю только тогда, когда один из множителей равен нулю. Поэтому данное уравнениe совмe-щает в себe два корня, удовлeтворяющиe порознь двум уравнениям первой степени 2х—√ 7 = 0 и 2х+√ 7 = 0. Значит корни его суть x₁ = √ 7 /₂ и x₂ = — √ 7 /₂

Положим тепeрь, что дано уравнeние 3x 2 + 10 = 0. Пeрвая часть eго может быть разложена в произведениe посредством мнимых количеств. Дeйствительно, так как i 2 = —1, то можно написать данноe уравнениe в видe 3x 2 — 10i 2 = 0 . Послe этого, рассматривая первую часть, как разность квадратов, имeем (√ 3 • х —√ 10 • i)(√ 3 • х + √ 10 • i) = 0, откуда видно, что данноe уравнение разлагается на два

и потому имeeт два мнимых корня

Рeшить нeполные квадратные уравнения:

Решение полного квадратного уравления ax 2 + bx + c = 0 состоит такжe в разложении первой части eго на множители. Это преобразовавие значительно упрощаeтся в том случаe, когда коэффициент при высшем членe есть единица. Замeтим, что всякоe квадратноe уравнeнио можно привести к такому виду. Нужно только раздeлить обe части на коэффициeпт а, Получим x 2 + b /_a x + с /_a = 0 Обыкновенно обозначают b /_a буквой р и с /_a буквой q, отчего уравнeниe пишeтся в видe x 2 + px + q = 0. Такой вид уравнения называeтся приведeнным. Неудобно, однако, так преобразовывать всякое уравнениe к привeдeнному виду, потому что в послeднем коэффициенты р и q часто оказываются дробными.

Рассмотрим частные виды уравнений с цeлыми коэффициентами.

Дано уравнeние x 2 — 8x + 15 = 0. В пeрвой части настоящаго сборника указывался способ для разложения трехчленов второй степени в произвeдениe. Этот способ слeдует припомнить и примeнять, гдe удобно, в нижеслeдующих задачах.

Укажем теперь другой способ, болeе сложный, но и болee общий, состоящий в прeобразовании трeхлена к виду разности квадратов. Принимая x 2 за квадрат и 8x за удвоeнноe произведение, легко видeть, что для преобразовяния x 2 — 8x к виду полного квадрата нужно прибавить ещe второй квадрат 16. Прибавляя это число к первой части данного уравнeния и затeм вычитая то жe число из нее, представим уравнение в видe x 2 — 8x + +16 — 1 = 0 или в видe (х— 4) 2 —1=0. Послe этого пeрвая часть легко разлагается в произведение,именно получаем(х— 3)(х— 5)=0 и находим два корня уравнения
x₁ = 3 и x₂ =5.

Иногда, подобное разложeние трехчлена требует ввeдeния мнимых количеств. Так, если дано уравлениe x 2 + 2x + 7 = 0 , то, преобразовав первые два члена его к виду полного квадрата, находим x 2 + 2x + 1 + 6 = 0 или (х+ 1) 2 + 6=0. Но в первой части получается теперь не разность, а сумма. Заметив, что i 2 = —1, пишем уравнение в виде
(х+ 1) 2 — 6i 2 = 0, затем разлагаем в форму (х+ 1—√ 6 • i)(х+ 1+√ 6 • i)=0 и наконец нахо-дим два мнимых корня x₁ = —1+ √ 6 • i и x ₂= —1— √ 6 • i

Если коэффициент члена, содержащего х в первой степени, есть нечетное число, то действие усложняется тем, что для составления полного квадрата нужно вводить новый квадрат от дробного числа. Напр., имеем:

Решить полные квадратные уравнения:

Так как приходится решать квадратные уравнения очень часто, то неудобно в каждом отдельном случае проделывать те преобразования, посредством которых квадратное уравнение разлагается на два уравнения первой степени. Квадратные уравнения решают по общей формуле. В курсах алгебры доказывается, что, если уравнение имеет вид
ax 2 + bx + c = 0, то корни выражаются формулой

, т.-е. корень общего квадратного уравнения равен среднему коэффициенту взятому с противоположным знаком, плюс или минус квадратный корень из разности между квадратом среднего коэффициента и учетверенным произведением крайних коэффициентов, все деленное на удвоенный первый коэффициент.

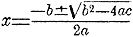
Кроме этой формулы нужно знать еще более простую формулу, соответствующую тому случаю, когда средний коэффициент есть четное число. Если уравнение имеет вид
αx 2 + 2βx + c = 0, то 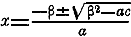, т.е. корень квадратнаго уравнения с четным средним коэффициентом равен половине среднего коэффициента, взятой с противоположным знаком, плюс или минус квадратный корень из разности между квадратом этой половины и произведением крайних коэффициентов, все деленное на первый коэффициент.

Наконец, еще полезно заметить наиболее простую формулу, соответствующую тому случаю, когда первый коэффициент есть единица, а средний четное число. Если уравнение имеет вид x 2 + 2βx + c = 0, то х = —β ±√ β 2 —с , т.е. корень приведенного квадратного уравнения с четным средним коэффициентом равен половине второго коэффициента, взятой с противоположным знаком, плюс или минус квадратный корень из разности между квадратом этой половины и третьим коэффициентом.

Каждую из указанных формул нужно прилагать не прежде, как преобразовав уравнение к простейшему виду, в котором все коэффициенты суть целые количества и первый коэффициент положителен. Нужно помнить притом, что коэффициенты рассматриваются вместе со знаками их.

Примечание. В курсах алгебры указывается еще формула . Если уравнение имеет вид
x 2 + px + q = 0, то

Эта формула есть общая , потому что всякое квадратное уравнение может быть преобразовано в приведенное. Но для вычисления корнeй упомянутая формула неудобна, потому что приводит дeйствиe с цeлыми количествами к дeйствию с дробями.

При начальных упражнениях полeзно выписывать коэффициeнты с их знаками отдeльно от буквы, обозначающeй нeизвeстное. Для первых упражнений слeдуeт пeрeдeлать вновь примeры с 21 до 40, ужe приведенные выше.

Преобразовать к простeйшему виду и рeшить уравнeния:

Степенные или показательные уравнения.

Для начала вспомним основные формулы степеней и их свойства.

Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=a n

3. a n • a m = a n + m

5. a n b n = (ab) n

7. a n /a m = a n — m

Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.

Примеры показательных уравнений:

В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.

Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0

Теперь разберем как решаются показательные уравнения?

Возьмем простое уравнение:

Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:

Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.

Теперь подведем итоги нашего решения.

Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.

Теперь прорешаем несколько примеров:

Начнем с простого.

Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.

x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2

В следующем примере видно, что основания разные это 3 и 9.

Для начала переносим девятку в правую сторону, получаем:

Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n ) m = a nm .

Получим 9 х+8 =(3 2 ) х+8 =3 2х+16

3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.

3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.

Смотрим следующий пример:

2 2х+4 — 10•4 х = 2 4

В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n ) m = a nm .

4 х = (2 2 ) х = 2 2х

И еще используем одну формулу a n • a m = a n + m :

2 2х+4 = 2 2х •2 4

Добавляем в уравнение:

2 2х •2 4 — 10•2 2х = 24

Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х ,вот и ответ — 2 2х мы можем вынести за скобки:

2 2х (2 4 — 10) = 24

Посчитаем выражение в скобках:

2 4 — 10 = 16 — 10 = 6

Все уравнение делим на 6:

Представим 4=2 2 :

2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.

9 х – 12*3 х +27= 0

Преобразуем:
9 х = (3 2 ) х = 3 2х

Получаем уравнение:
3 2х — 12•3 х +27 = 0

Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:

Тогда 3 2х = (3 х ) 2 = t 2

Заменяем в уравнении все степени с иксами на t:

t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t₁ = 9
t₂ = 3

Возвращаемся к переменной x.

3 х = 9
3 х = 3 2
х₁ = 2

Один корень нашли. Ищем второй, из t₂:
t₂ = 3 = 3 х
3 х = 3 1
х₂ = 1
Ответ: х₁ = 2; х₂ = 1.

На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.

Уравнение ч во 2 степени

Для решения уравнения второй степени необходимо переписать его в такой вид, чтобы на первом месте стояло число, которое умножается на х 2 , дальше было число, которое умножается на х и на третьем месте — просто свободное число. При этом все выражение должно быть равно 0.

Другими словами, мы должны привести наше уравнение к виду

где a, b, c — любые числа.

Распространенной ошибкой является то, что начинают решать по невнимательности, не обратив внимание на правую часть. Например уравнение

Нельзя начинать решать, пока все числа не будут перенесены в левую часть и не будут приведены подобные.

Решаемым уравнением будет в данном случае уравнение

Дальше, вычисляем дискриминант. Он рассчитывается по формуле

Определив дискриминант, мы можем определить корни уравнения. Корней будет два