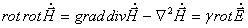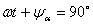Уравнение даламбера для скалярного и векторного потенциалов

Тема 11. Электродинамические потенциалы. Основные теоремы и принципы электродинамики

Постановка задач в электродинамике. Скалярный и векторный электродинамические потенциалы. Уравнения Даламбера для электродинамических потенциалов. Уравнения Пуассона и Лапласа. Связь электродинамических потенциалов с векторами ЭМП. Решение неоднородных уравнений Даламбера для электродинамических потенциалов. Запаздывающие потенциалы.

Применение электродинамических потенциалов в анализе ЭМП.

Основные теоремы и принципы в теории гармонических полей. Магнитные токи и заряды. Принцип перестановочной двойственности уравнений Максвелла. Теорема единственности для внешней и внутренней задач электродинамики. Принцип эквивалентности. Различные формулировки принципа эквивалентности. Лемма Лоренца. Сопряженная лемма. Теорема взаимности.

Указания к теме

Необходимо выучить определения скалярного и векторного потенциалов, обратить внимание на их связь с векторами и энергией ЭМП, а также на применение в анализе ЭМП; уяснить понятие запаздывающего потенциала.

Пользуясь теоремой Пойнтинга о балансе энергии, можно определить дополнительные условия, наложение которых сообщает решениям уравнений Максвелла физическую определенность (единственность).

Следует выучить формулировки теорем единственности и взаимности, принципов эквивалентности и двойственности, обратить внимание на их место в теории ЭМП.

Основные сведения

При решении задач излучения необходимо решать систему уравнений Максвелла при наличии сторонних источников ЭМП. Введение электродинамических потенциалов позволяет упростить расчет ЭМП излучающих систем. Из условия соленоидальности магнитного поля (2.8) можно записать:

Þ , (11.1)

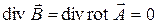
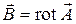
где введенную функцию называют векторным потенциалом.

Подстановка выражения (11.1) в (2.6) позволяет связать с :

или . (11.2)

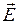
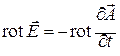
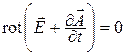
Из условия потенциальности электростатического поля

Þ , (11.3)

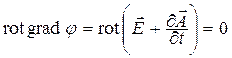
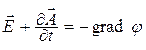
где введенную функцию j называют скалярным потенциалом (в случае электростатического поля функция jявляется скалярным электрическим потенциалом)[1, 11].

Векторы ЭМП можно выразить через и j :

, . (11.4)

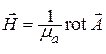
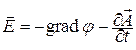
Волновые уравнения для электродинамических потенциалов.Подставляя выражение (11.4) в систему уравнений Максвелла для однородной среды при наличии сторонних источников ЭМП, получаем

. (11.5)

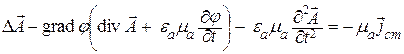
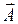
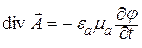
Удобно выбрать div так, чтобы в уравнении (11.5) слагаемое в скобках оказалось бы равным нулю

. (11.6)

Условие (11.6) называют калибровкой Лоренца. В случае равенства нулю правой части (11.6) получается калибровка Кулона [1–3, 11].

С учетом выражения (11.6) из системы уравнений Максвелла получаются неоднородные волновые уравнения для потенциалов и j

; (11.7)

. (11.8)

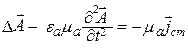
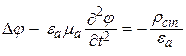
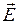
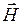
После решения уравнений (11.7) и (11.8) для конкретных исходных данных векторы и находятся после подстановки и j в (11.4).

В случае стационарного магнитного поля можно считать потенциальной энергией токов, в то же время j связан с потенциальной энергией зарядов в электростатике [1–3].

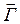
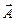
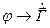
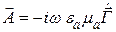
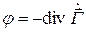
При решении задач излучения с целью уменьшения числа неизвестных иногда вводят вектор Герца [12] ( , ).

, . (11.9)

В классической электродинамике и j – лишь вспомогательные величины, так как для представления ЭМП необходим переход к и . В квантовой электродинамике и j считаются фундаментальными величинами [1–3].

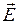
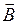
Электродинамические потенциалы в безграничном пространстве.Решение уравнений (11.7) и (11.8) в безграничном пространстве упрощается. В пространстве вне точечного источника r_ст = 0.

Для точечного заряда в ССК и ЦСК решение имеет вид [1–4]

. (11.10)

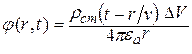
При v®¥ (мгновенное распространение действия ЭМП) из уравнений (11.8) получается уравнение С. Пуассона [1, 6, 11] : .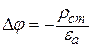

При точках незаряженной области (r = 0) уравнение Пуассона (11.15) переходит в уравнение П. Лапласа [6, 11] : .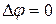

Волновое уравнение для векторного потенциала имеет вид [1–3, 11]

(11.11)

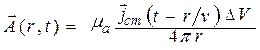
Полученные решения (11.10) и (11.11) отражают конечность скорости распространения ЭМП от своих источников. В точке наблюдения значения электродинамических потенциалов (а значит, и векторов ЭМП) определяются значением не в текущий момент времени t, а в предшествующий момент t – r/v. Поэтому решения (11.10) и (11.11) называют запаздывающими потенциалами. Время запаздывания r/v как раз показывает, какое время требуется ЭМВ, чтобы пройти расстояние r с конечной скоростью v [11].

Сравнивая уравнения (11.10) и (11.11) с (5.5) и (5.6), можно сделать вывод, что полученные решения имеют характер сферических волн.

При решении задач электродинамики выделяют внутреннюю и внешнюю задачи. Внутренней называется задача определения ЭМП внутри области V, ограниченной замкнутой поверхностью S (рис. 11.1), при заданных на ней граничных условиях для векторов ЭМП. Примеры внутренней задачи – определение ЭМП в объемном резонаторе, определение функции распределения тока в антенне заданной конструкции.

Внешняя задача электродинамики заключается в решении уравнений Максвелла для неограниченного пространства вне области V, ограниченной замкнутой поверхностью S , при наличии источников ЭМП. Примеры внешней задачи – определение ЭМП антенны в свободном пространстве при известном распределении тока в антенне, решение задач дифракции.

При постановке задач электродинамики необходимо ввести начальные и граничные условия, сообщающие этим задачам физическую определенность [1]. Векторы ЭМП не могут иметь произвольную зависимость от координат и времени. Например, есть ограничения на скорость убывания амплитуд 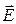и .

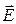
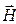
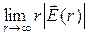
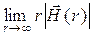
Из закона сохранения энергии следует [1], что в пространстве без потерь каждый из векторов и должен убывать не медленнее, чем 1/r . Это условие называется условием излучения на бесконечности [1]:

= 0 ; = 0 . (11.12)

Условия (11.12) эквивалентны условиям излучения Зоммерфельда

= 0 ; = 0 . (11.13)

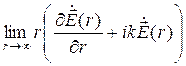
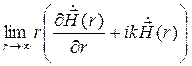
Знак при вторых слагаемых в уравнениях (11.13) определяет, что условия записаны для ЭМВ, которая расходится (удаляется) от источника [1, 5]. При наличии потерь в пространстве, которые учитываются коэффициентом затухания a, векторы ЭМП убывают быстрее – пропорционально exp(–ar)/r.

Существуют принципы и теоремы электродинамики, которые позволяют существенно упростить решение задач электродинамики и теории антенн.

Теорема единственности решений уравнений Максвелла.Методы решения уравнений ЭМП могут быть различными, поэтому необходимо доказать, что решение, полученное любым методом, является единственным. В учебных пособиях [1, 12] приведено доказательство того, что если при решении уравнений Максвелла при определенных начальных и граничных условиях получены значения векторов ЭМП ( 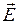и ), то это решение будет единственным.

Принцип двойственности. Для решения задач теории ЭМП удобно ввести понятия магнитных токов и зарядов. Как отмечалось ранее, эти величины являются фиктивными и вводятся как эквивалент действия электрических токов.

При наличии магнитных источников уравнения Максвелла (2.20)–(2.21) уступают место следующим [1, 13]:

= = , , (11.14)

= = , . (11.15)

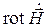
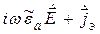
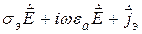
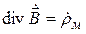
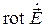
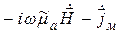
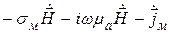
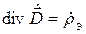
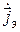
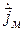
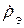
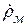
где и – плотности сторонних электрического и магнитного токов соответственно; s_м – удельная эквивалентная магнитная проводимость; и – объемные плотности электрического и магнитного зарядов.

Сопоставляя уравнения Максвелла и выражения (11.14)–(11.15), нетрудно убедиться, что одни полностью переходят в другие при следующей замене:

® , ® , ® , ® , ® , e_a « µ_a , s_э « s_м,

, ® – , ® – , ® – , ® – , ® – . (11.16)

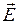
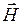
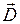
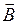
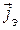
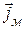
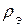
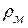
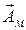
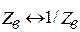
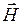
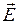
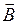
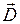
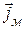
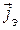
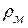
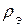
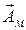
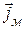
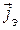
Следует отметить, что размерности эквивалентных величин несколько отличаются от обычных в системе СИ. Оказывается, что измеряется в вольтах на метр квадратный, а не в амперах на метр квадратный, как , I_м – в вольтах (размерность U), Q_м – в веберах (размерность Ф), s_м – в омах на метр (размерность удельного сопротивления) [1, 7], то есть размерности прямой и обратной замены отличаются как сопротивление и проводимость!

Таким образом, если найдено ЭМП заданных электрических источников, то достаточно сделать замену (11.16) в готовом решении задачи, и это непосредственно приведет к выражению ЭМП излучения магнитных источников.

Общий смысл принципа двойственности состоит в том, что при определенных условиях электрическое и магнитное поля «меняются ролями». Кроме того, симметрия системы уравнений Максвелла (11.14)–(15.9) подчеркивает равноправие электрических и магнитных составляющих в переменном ЭМП.

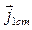
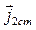
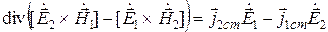
Лемма Лоренца. Пусть в некоторой линейной среде имеется два электрических источника, характеризуемых функциями плотности стороннего электрического тока и соответственно (рис. 11.2). После преобразований

. (11.17)

Интегрируя уравнение (11.17) по области V, ограниченной поверхностью S, охватывающей источники ЭМП, с учетом теоремы Остроградского – Гаусса (2.11) получим

. (11.18)

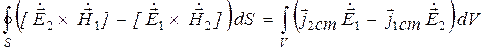
Соотношения (11.17) и (11.18) – это соответственно дифференциальная и интегральная формулировки леммы Лоренца, устанавливающей важные связи между полями двух источников.

В случае свободного пространства в дальней зоне источников (S®∞) левая часть соотношения (11.18) стремится к нулю [1, 5, 6], а это приводит к таким соотношениям:

, . (11.19)

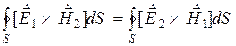
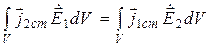
Принцип взаимности разделенных источников. В случае, когда источники разделены в пространстве, первый источник расположен в области V₁, а второй – в области V₂ (рис. 11.2), соотношения (11.19) принимают форму

. (11.20)

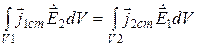
Интеграл справа можно истолковать как некоторую характеристику взаимодействия ЭМП первого источника с ЭМП второго; аналогичный смысл имеет интеграл слева. Очевидно, что характеристики такого рода равны независимо от типа источников и изотропных сред, в которых они расположены.

Соотношение (11.20) выражает принцип взаимности, подразумевая пространственно разделенные источники и их поля.

Для двух линейных токов из выражения (11.20) следует [1]

, (11.21)

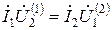
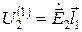
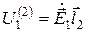
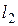
где и представляют собой э. д. с., наводимые на каждом из линейных элементов (I1) и (I2) полем другого источника.

Равенство (11.21) можно представить в другой форме:

Þ , (11.22)

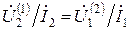
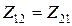
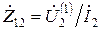
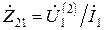
где и имеют смысл взаимных сопротивлений.

Принцип взаимности проявляется в том, что э. д. с., наводимая на первом элементе заданным током второго, оказывается такой же, как и э. д. с. на втором элементе при равном токе первого [1].

Э. д. с., наводимая в приемной антенне в зависимости от ее ориентации, изменяется по тому же закону, что и ЭМП в дальней зоне, создаваемое этой антенной в режиме передачи. То есть направленность действия антенны при приеме и передаче одинакова. В теории антенн принцип взаимности позволяет использовать характеристику направленности передающей антенны (ДН) при использовании этой антенны в качестве приемной, а также использовать измеренную характеристику ДН приемной антенны и в режиме передачи.

Среды, устройства и системы, в которых выполняется принцип взаимности, называют взаимными [1].

Список рекомендуемой литературы:[1, гл. 11, 15, с. 55–59, 83–90; 2, с. 75–78, 123–126, 132–139, 150–152; 3, гл. 11, с. 51–55; 4, с. 47–50; 5, с. 21–24, 52–55, 223–239; 6, с. 128–138, 172, 205–212; 7, с. 63–67, 244–279; 8, с. 18–25, 57–61; 9, с. 60–61, 143–154, 157–159; 10, с. 68–70; 11, с. 61–75, 121–125; 12, с. 63–65, 94–98, 106–132; 13, с. 134–140, 150–155, 165–168, 238–241; 32, с. 13–17; 34, с. 5–10; 35, с. 11–13; 36, с. 9–12].

Контрольные вопросы и задания

1. Дайте определение электродинамическим потенциалам ЭМП.

2. Что дает введение электродинамических потенциалов?

3. Почему потенциалы называют «запаздывающими»?

4. Существует ли связь электродинамических потенциалов с энергией ЭМП?

5. С помощью какого из электродинамических потенциалов можно охарактеризовать потенциальную энергию зарядов в электростатическом поле?

6. Какой потенциал связан с потенциальной энергией токов в случае стационарного магнитного поля?

7. Каково место электродинамических потенциалов в теории ЭМП и теории антенн?

8. Укажите условия калибровки волновых уравнений для электродинамических потенциалов. Зачем нужны условия калибровки?

9. Можно ли скалярный потенциал назвать «электростатическим»?

10. Существуют ли магнитные токи и заряды?

11. Дайте определение внешней и внутренней задач электродинамики.

12. В чем смысл принципа двойственности?

13. Назовите формулировку теоремы единственности. Какие требования предъявляются к функциям, описывающим ЭМП для выполнения теоремы единственности?

14. Дайте формулировку принципа эквивалентности.

15. В чем заключается смысл теоремы взаимности?

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЕННОСТЬ

Факт взаимодействия электрических зарядов на расстоянии можно объяснить наличием вокруг них электрического поля — материального объекта, непрерывного в пространстве и способного действовать на другие заряды.

Поле неподвижных электрических зарядов называют электростатическим.

Характеристикой поля является его напряженность.

Напряженность электрического поля в данной точке — это вектор, модуль которого равен отношению силы, действующей на точечный положительный заряд, к величине этого заряда, а направление совпадает с направлением силы.

Напряженность поля точечного заряда Q на расстоянии r от него равна

2.Передача электромагнитной энергии вдоль проводов линии.

Билет 20

1. Поле заряженной оси и цилиндра.

Под заряженной осью понимают тонкий, теоретически бесконечно длинный металлический проводник.

Под линейной плотностью заряда t понимают заряд, приходящийся на единицу длины оси.

Пусть диэлектрическая проницаемость окружающей среды равна e_a.

Для нахождения напряженности поля в некоторой точке, удаленной на расстояние r от оси, проведем через точку цилиндрическую поверхность так, чтобы ее ось совпала с заряженной осью (рис. 15.6).

Рис. 15.6. К определению поля заряженной оси

Используем теорему Гаусса, которая применима к замкнутой поверхности (боковая поверхность цилиндра и два его основания). Поток вектора имеется только через боковую поверхность. Направление и на боковой поверхности в каждой точке совпадают, поэтому

(15.25)

Напряженность в поле заряженной оси изменяется обратно пропорционально расстоянию r точки от оси.

(15.26)

Потенциал изменяется по экспоненциальному закону.

Электрическая емкость определяется как отношение заряда к разности потенциалов между телами. Рассчитаем емкость двух соосных цилиндров (рис. 15.7).

Рис. 15.7. Разрез двух соосных цилиндров

Напряжение между поверхностями цилиндров

.

Емкость цилиндрического конденсатора будет равна

(15.27)

2. Излучение электромагнитной волны. Уравнение Даламбера.

3. Будем исходить из уравнения Максвелла . Домножим обе части на и учтем, что и . получим:

4. .

5. Учтем, что и . Тогда получим

6.

7.

8. . (28.1)

9. Пользуясь неоднозначностью потенциалов, определяемых с точностью до калибровочного преобразования, для максимального упрощения наложим на них условие:

10. (28.2)

11. И тогда из (28.1) получим уравнение Даламбера:

12. (28.3)

13. Условие (28.1) называется условием калибровки Лоренца. Получим теперь уравнение для скалярного потенциала следующим образом:

14. и учтем, что . Тогда

15. .

16. Из (28.2): . Тогда получим

17. (28.4)

18. Уравнение (28.4) тоже уравнения Даламбера. Следовательно, для скалярного и векторного потенциалов получили одно и тоже уравнение.

19. (28.5)

20. Где — скорость электромагнитных волн в среде. Уравнение (28.5) – уравнение гиперболического типа и описывает волновой процесс, т. е. волны, распространяющиеся в пространстве со скоростью . В одномерном случае при решение (28.5) можно представить в виде суммы двух функций:

21. . (28.6)

22. Которое описывает волны, распространяющиеся в двух противоположных направлениях. Функция представляет собой волну, движущуюся в направлении положительных значений оси Ох со скоростью , а — в противоположном направлении.

23. Рассмотрим решение волнового уравнения в сферически симметричном случае, т. е. считая, что в (28.5) F=0, а Ф=Ф(R), где R – расстояние от начала координат до рассматриваемой точки. В этом случае Ф от углов не зависит и оператор Лапласа имеет вид

24. . (28.7)

25. Поэтому волновое уравнение для Ф записывается в виде

26. . (28.8)

27. Решением этого уравнения для 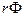, как и в предыдущем случае, являются произвольные функции от аргумента и , т. е. общее выражение для Ф таково:

28. . (28.9)

29. Функция Представляет волну, движущуюся в радиальном направлении от начала координат со скоростью . Форма волны при этом не изменяется, а амплитуда уменьшается как 1/R. Эта волна называется расходящейся. Функция представляет сходящуюся к началу координат волну.

30. Потенциалы поля, а следовательно, и сами поля распространяются в свободном пространстве со скоростью . В вакууме , , поэтому скорость распространения полей равна скорости света . Таким образом Электромагнитные волны и всякие изменения электрического и магнитного поля распространяются в вакууме со скоростью света. А это означает, что электромагнитные взаимодействия распространяются со скоростью света. Например, если два точечных заряда покоятся на расстоянии R друг от друга и один из зарядов в некоторый момент сдвинут со своего места, то другой заряд «почувствует» этот сдвиг лишь спустя время .

Билет 21

1. Электростатическое поле и ёмкость коаксиального кабеля

К оаксиальный кабель представляет собой два металлических соосных цилиндра, расположенных один внутри другого и изолированных друг от друга диэлектриком с проницаемостью ε_а (рис.11.18). Такой кабель широко применяется на высоких частотах. Пусть внутренний цилиндр, который называется жилой, несёт на себе заряд +τ, а наружный цилиндр (оболочка) – заряд –τ. Тогда возникнет электростатическое поле, расчёт которого произведём для отдельных областей кабеля. Внутри жилы (0>r>r₁) поля нет, так как жила проводящая, т.е.E=0, φ=const. Для определения напряжённости поля в пространстве между жилой и оболочкой воспользуемся теоремой Гаусса: В качестве поверхности интегрирования возьмём цилиндр радиуса r и длиной l. Поток вектора Е через донышки этого цилиндра равен нулю (векторы Е и ds перпендикулярны), а через его боковую поверхность Тогда Так как Е имеет только радиальную составляющую, то

Для всех точек оболочки кабеля (r_{2 3}) E=0, φ=const, так как она проводящая. За пределами кабеля (r₃

Ёмкость коаксиального кабеля С= где q=τl, a

Тогда , а

2. Переменное электромагнитное поле в проводящей среде.

Проводящая среда предполагается однородной и изотропной. Уравнения Максвелла для проводящей среды в комплексной форме записи.

	(4.14)
(4.15)

Уравнения записаны для мгновенных значении. Если и во времени изменяются по синусоидальному закону, то можно воспользоваться символическим методом для их записи. И будем обозначать:

— комплекс действующего значения синусоидального изменяющегося вектора напряженности (проекция вектора на любую ось изменяется по синусоидальному закону).

Очевидно, что однократное дифференцирование вектора по времени приводит к умножению его комплексной амплитуды или комплекса действующего значения на , а двукратное умножение на .

Итак, уравнения Максвелла в комплексной форме с учетом :

(4.14):		(4.16)
(4.15):	(4.17)

Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью и магнитной проницаемостью .

В проводящей среде даже при весьма высоких частотах . В настоящее время наука не располагает точными данными о числовом значении относительной магнитной проницаемости для металлов. Имеются лишь сведения, что порядок для металлов такой же, как и для большинства диэлектриков, то есть от нескольких единиц до нескольких десятков.

Например, для меди . Найдем, во сколько раз ток проводимости будет больше тока смешения при :

,

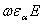
то есть даже на очень высоких частотах ток проводимости гораздо больше тока смещения.

(4.16):

(4.18)

Уравнения (4.17) и (4.18) представляют собой уравнения с 2-мя неизвестными: 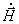и . Проведем их совместное решение. С этой целью возьмем ротор от уравнения (4.18):

Учтем, что , поэтому .

С учетом (4.17): ,

(4.19)

уравнение (4.19) является дифференциальным относительно 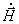. В самом общем случае, когда зависит от 3х или даже от 2х координат, решение (4.19) – сложно. Поэтому ограничимся рассмотрением решения (4.19) для частного случая — для плоской и для цилиндрической электромагнитной волны

Билет

(1)Поле и емкость плоского конденсатора.

Конденсаторы состоят из двух или более близко расположенных друг к другу проводников (обкладок), разделенных слоем диэлектрика (рис. 1), причем толщина слоя диэлектрика между проводниками значительно меньше размеров самих проводников.

При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.

Обкладкам конденсатора сообщают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов, так как разноименные заряды притягиваются и поэтому располагаются на внутренних поверхностях пластин.

Под зарядом конденсатора понимают заряд одной пластины.

Электроемкостью конденсатора называют физическую величину, численно равную отношению заряда конденсатора к разности потенциалов между его обкладками:

Обозначим площадь одной обкладки S, расстояние между ними d.

Следовательно, емкость плоского конденсатора

Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей (рис. 2, а и б). Напряженность поля (рис. 2, в) можно найти по принципу суперпозиции

— напряженность поля конденсатора, где — поверхностная плотность заряда на обкладках конденсатора.

2. Плоская волна в проводящей среде. Преломление и отражение плоской волны.

Плоская волна в проводящей среде

Рассмотрим распространение плоской электромагнитной волны в проводящей среде, которая простирается теоретически в бесконечность.

Электромагнитная волна проникает из диэлектрика в проводящую среду и распространяется в ней. Так как среда теоретически бесконечна и падающая волна не встречает границы, которая изменила бы ее распространение, то отраженной волны в данном случае не возникает.

,

.

Так как и : ,

Постоянную интегрирования найдем из пограничных условий. Если обозначить напряженность магнитного поля на поверхности проводящей среды через , то при и :

,

,

Чтобы записать выражения для линейных значений и необходимо правые части и умножить на и взять мнимые части от полученных произведений. Получим:

	(4.24)
	(4.25)

Проанализируем выражения (4.24) и (4.25)

амплитуда

амплитуда .

По мере увеличения я множитель уменьшается по показательному закону, следовательно, по мере проникновения электромагнитной волны в проводящую среду, амплитуды и уменьшаются по показательному закону.

Если принять то кривая получена при

Для того чтобы охарактеризовать, насколько быстро уменьшается амплитуда падающей волны по мере проникновения в проводящую среду, вводят понятие глубины проникновения.

5. Глубина проникновения и длина волны

Под глубиной проникновения понимают расстояние вдоль направления распространения волны (ось Z), на котором амплитуда падающей волны (или ) уменьшается в раз. Глубину проникновения определяют с помощью выражения:

.

Билет

.(1)Применение принципа суперпозиции для расчета полей.

Основной задачей электростатики является определение величины и направ­ле­ния вектора напряженности в каждой точке поля, создаваемого либо системой неподвижных точечных зарядов, либо заряженными поверхностями произвольной формы. Рассмотрим первый случай, когда поле создано системой зарядов q₁, q₂. q_n. Если в какую-либо точку этого поля поместить пробный заряд q₀, то на него со стороны зарядов q₁, q₂. q_n будут действовать кулоновские силы . Со­гласно принципу независимости действия сил, рассмотренного в механике, равно­дей­ствующая сила равна их векторной сумме

.

Используя формулу напряженности электростатического поля, левую часть ра­венства можно записать: , где — напряженность результирующего поля, создаваемого всей системой зарядов в точке, где расположен пробный заряд q₀. Пра­вую часть равенства соответственно можно записать , где — напря­женность поля, создаваемая одним зарядом q_i. Равенство примет вид . Сокращая на q₀, получим .

Напряженность электростатического поля системы точечных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из этих зарядов в отдельности. В этом заключается принцип независимости действия электростатических полей или принцип суперпозиции (наложения) полей.

Обозначим через радиус-вектор, проведенный из точечного заряда q_i в ис­следуемую точку поля. Напряженность поля в ней от заряда q_i равна . Тогда результирующая напряженность , создаваемая всей системой зарядов равна . Полученная формула применима и для расчета электростатических полей за­ря­женных тел произвольной формы так как любое тело можно разделить на очень малые части, каж­дую из которых можно считать точечным зарядом q_i. Тогда расчет в любой точке пространства будет аналогичен выше приведенному.

Длина волны λ — это расстояние между двумя ближайшими точками оси X, в которых колебания значений поля происходят в одинаковой фазе

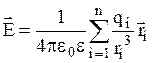
(в частности — между двумя ближайшими максимумами поля, как на рис. 5).

Частота, с которой меняются значения E и B в данной точке пространства, называется частотой электромагнитной волны; она совпадает с частотой ν колебаний излучающего заряда. Длина электромагнитной волны λ, её частота ν и скорость распространения c связаны стандартным для всех волн соотношением: c = λν.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 25

1. Расчет электрической емкости.

2. Эффект близости. Поверхностная закалка индукционным методом.

1. Поле точечного заряда в однородной среде.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.

4.3. Электродинамические векторный и скалярный потенциалы

Для удобства исследования электромагнитного (так же как и при рассмотрении статических и стационарных полей) поля вводят в рассмотрение векторный магнитный потенциал и скалярный электрический потенциал.

Естественно, что при этом эти потенциалы являются функциями не только координат, но и времени. При этом векторный магнитный потенциал связан с вектором магнитной индукции посредством уравнения (3.6) (что вытекает из закона непрерывности магнитного потока), а скалярный потенциал электромагнитного поля U удовлетворяет следующему уравнению:

Кроме данного уравнения (с целью упрощения) скалярный потенциал связывают с векторным потенциалом посредством ввода так называемого калибровочного условия

.

После подстановки этих потенциалов в уравнения Максвелла и некоторых преобразований (с учетом условия (4.10)), получают для них уравнения Даламбера

(4.12)

Здесь – плотность тока проводимости.

В области, где нет свободных зарядов (r=0) и нет токов проводимости и переноса уравнения (4.11) и (4.12) приобретают вид волновых уравнений:

Переменное электромагнитное поле создается токами и зарядами, зависящими не только от координат, но и от времени (r=r(x,y,z,t), d=d(x,y,z,t), поэтому решение уравнений (4.11) и (4.12) в сферической системе координат может быть представлено в следующем виде:

Здесь – значение вектора плотности тока в элементе объема dv в момент времени (t-r/u), предшествующий моменту времени t, в который определяется векторный потенциал; – значение объемной плотности заряда в момент времени (t-r/u), предшествующий моменту времени t, в который определяется U.

В связи с этим, скалярный U и векторный А потенциалы, выраженные формулами (4.13) и (4.14) называют электродинамическими запаздывающими потенциалами.

Наиболее часто понятием запаздывающих потенциалов пользуются в радиотехнике при рассмотрении вопросов, связанных с излучением электромагнитной энергии.