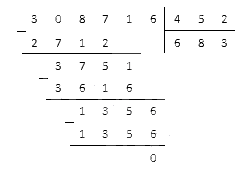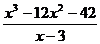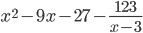Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)
С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена
Немного теории.
Деление многочлена на многочлен (двучлен) столбиком (уголком)
В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).
Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.
Для любых многочленов \( f(x) \) и \( g(x) \), \( g(x) \neq 0 \), существуют единственные полиномы \( q(x) \) и \( r(x) \), такие что
$$ \frac
причем \( r(x) \) имеет более низкую степень, чем \( g(x) \).
Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного \( q(x) \) и остатка \( r(x) \) для заданных делимого \( f(x) \) и ненулевого делителя \( g(x) \)
Пример
Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ \frac
Частное и остаток от деления данных многочленов могут быть найдены в ходе выполнения следующих шагов:
1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой \( (x^3/x = x^2) \)
|
|
2. Умножаем делитель на полученный выше результат деления (на первый элемент частного). Записываем результат под первыми двумя элементами делимого \( (x^2 \cdot (x-3) = x^3-3x^2) \)
|
|
3. Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой \( (x^3-12x^2+0x-42-(x^3-3x^2)=-9x^2+0x-42) \)
|
|
4. Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
|
|
5. Повторяем шаг 4.
|
|
6. Конец алгоритма.
Таким образом, многочлен \( q(x)=x^2-9x-27 \) — частное деления многочленов, а \( r(x)=-123 \) — остаток от деления многочленов.
Результат деления многочленов можно записать в виде двух равенств:
\( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 \)
или
$$ \frac
Деление целых чисел: правила, примеры
Данная статья рассказывает о том, как делить без остатка целые числа, то есть нацело. Будут введены термины и обозначения для дальнейшего описания чисел, деление положительных и отрицательных чисел. В итоге произведем проверку вычислений.
Термины и обозначения
При делении целых чисел используются те же термины, что и при описании натуральных чисел.
Делимое – это число, над которым совершают деление.
Делитель – число, на которое делят.
Частное – результат деления.
Знак деления обозначают двоеточием « : » или знаком ÷ . Его расположение после делимого и перед делителем. Запись с использованием символов выглядит так: a : b . Результат записывается после знака равно « = ». Если при делении числа а на b получаем с , тогда запись выглядит в виде равенства a : b = c . Деление иначе называют частным.
Деление целых чисел
Между умножением и делением натуральных чисел существует связь. Это связано с тем, что при делении можно найти частное, которое при обратном действии будет считаться множителем. Иначе можно записать, что деление целых чисел служит нахождением одного из целых множителей.
Отсюда делаем вывод, что произведение целых чисел a и b с частным, равным с, можно представить обратным действием деления с на b с частным равным а . Если произведение чисел 5 и — 7 равна — 35 , отсюда имеем, что частное ( − 35 ) : 5 равняется — 7 , а ( − 35 ) : ( − 7 ) с результатом 5 .
Частное от деления считается целым тогда, когда получается результат без остатка, то есть целое число a должно делиться на число b с целым частным в результате.
Правила деления целых чисел
Смысл деления необходим для утверждения того, что одним из двух множителей является частным, а другой просто множителем. Таким образом не найти неизвестный множитель, имея известный множитель и произведение. Равенство 6 · ( − 7 ) = − 42 говорит о том, что результаты ( − 42 ) : 6 и ( − 42 ) : ( − 7 ) равняются — 7 и 6 соответственно. При известном произведении 45 , а одного из множителей — 5 , то смысл деления не даст прямого результата другого множителя.
Можно сделать вывод, что необходимо использовать правила, которые позволяют производить деление целых чисел. Они позволят делить целые и натуральные числа.
Деление целых положительных чисел
Целыми положительными числами называют натуральные числа, поэтому деление целых положительных чисел производится, исходя из правил деления натуральных чисел. Рассмотрим несколько примеров для детального просмотра деления целых положительных чисел.
Произвести деление целого положительного 104 на целое положительное 8 .
Для упрощения процесса деления можно представить число 104 в виде суммы 80 + 24 ,теперь необходимо применить правило деления суммы на данное число. Получим 104 : 8 = ( 80 + 24 ) : 8 = 80 : 8 + 24 : 8 = 10 + 3 = 13 .
Ответ: 104 : 8 = 13 .
Найти частное от деления 308 716 : 452 .
Решение
Когда имеем большое число, деление лучше всего производить в столбик:
Ответ: 308 716 : 452 = 683 .
Правило деления целых отрицательных чисел, примеры
Для формулировки правила необходимо применить рассуждения. Если необходимо поделить целые отрицательные числа a на b , то искомое частное получится равным с . Форма записи: a : b = c . После чего можно выяснить, чему равна абсолютная величина с .
Исходя из смысла деления равенство b · c = a справедливо. Значит, b · c = a . Благодаря свойствам модуля, можно записать равенство b · c = b · c , значит, и b · c = a . Отсюда получаем, что c = a : b . Абсолютная величина частного от деления равняется частному от деления модулей делимого и делителя.
Для определения знака числа с необходимо выяснить, какие знаки находятся перед делимым и делителем.
Исходя из смысла деления целых чисел, равенство b · c = a справедливо. Правило умножения целых чисел говорит о том, что частное должно быть положительным. Иначе, b · c будет производиться по правилам целых отрицательных чисел. Частное с от деления целых отрицательных целых чисел является положительным числом.
Объединить в правило деления: чтобы разделить целое отрицательное число на отрицательное, необходимо разделить делимый на делитель по модулю. Эта запись будет выглядеть так a : b = a : b , при а и b равными отрицательным числам.
Рассмотрим несколько примеров деления отрицательных чисел.
Разделить — 92 на — 4 .
Используя правила деления целых отрицательных чисел, получим, что следует делить по модулю. Получим, что — 92 : — 4 = — 92 : — 4 = 92 : 4 = 23
Ответ: ( − 92 ) : ( − 4 ) = 23 .
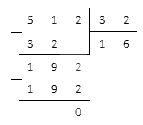
Вычислить — 512 : ( — 32 ) .
Решение
Для решения необходимо разделить числа по модулю. Деление производится столбиком.
Ответ: ( − 512 ) : ( − 32 ) = 16 .
Правило деления целых чисел с разными знаками, примеры
Выделим правило деления целых чисел, содержащих разные знаки.
Если делим целое числа a и b с разными знаками, то получаем число с . Необходимо определить знак получаемого числа. Следует записать c = a : b .
Чтобы определить смысл деления равенства b · c = a , необходимо рассмотреть два варианта. Предположительно существует вариант, когда а – отрицательное, b – положительное или а – положительное, а b – отрициательное. Любой из случаев в итоге имеет отрицательный результат. Следуя из правил умножения, имеем, что b и с отрицательные, тогда произведение будет являться положительным. Если b положительное, с – отрицательное, тогда произведение является отрицательным числом.
Для формулировки применимо правило деления целых чисел с разными знаками. Отсюда получим: чтобы разделить целые числа с разными знаками, необходимо разделить делимое на делитель по модулю, перед полученным результатом поставить « — ». Получаем, что a и b являются целыми числами с разными знаками. Это запишем, как a : b = — a : b .
Детально разберем примеры, где необходимо применить правило деления целых чисел с разными знаками.
Разделить 56 на — 4 .
Решение
Исходя из правила, имеем, что 56 необходимо разделить на 4 по модулю. Значит, получим, что 56 : 4 = 14 . Для определения знака результата необходимо посмотреть наличие « — » перед делителем и делимым. Если имеется только один знак минуса, то результат запишем как отрицательное значение. То есть, — 14 .
Ответ: 56 : ( − 4 ) = − 14 .
Выполнить деление — 1625 на 25 .
Данный пример показывает правильное деление целых чисел с разными знаками. Для этого необходимо применить правило
— 1625 : 25 = — — 1625 : 25 = — 1625 : 25 = — 65
Деление числа 1625 можно производить в столбик или с помощью представления его в виде суммы 1500 + 125 , применив правило деления полученной суммы на число.
Ответ: ( − 1 625 ) : 25 = − 65 .
Деление нуля на целое число
Деление нуля на любое целое число рассматривается как отдельная тема, так как имеет свои нюансы. По правилу частное от деления на любое целое число, отличное от нуля, равно нулю. Иначе можем записать, что 0 : b = 0 , где значение числа b отлично от нуля.
Для углубления в правило рассмотрим некоторые пояснения.
Допустим, что результат деления нуля на целое число равен с, тогда равенство b · c = 0 считается верным. Произведение в итоге дает ноль тогда, когда хотя бы один из них равен нулю. Если по условию b не равно нулю, тогда множитель с = 0 . Отсюда следует, что частное, полученное делением нуля на целое число, отличное от нуля, равняется нулю.
Например, при делении нуля на целое число, частное получаем равное нулю: 0 : 4 или 0 : — 908 . Оба результаты будут равны нулю.
Не делить на нуль
Деление целого числа на нуль не определяется, поэтому и запрещено производить деление на 0 .
Например, если при делении целого числа а на ноль получим число с, то из смысла деления должно быть справедливо равенство c · 0 = a . Правило умножения на нуль говорит о том, что c · 0 = 0 при любом значении с . Сравнивая оба равенства, получим, что, если делимое анне равно нулю, тогда равенство c · 0 = a считается неверным. Поэтому можно делать вывод о том, что деление на нуль производить нельзя.
Возможно ли деление нуля на самого себя? Допустим, что при делении получаем целое число с, тогда равенство c · 0 = 0 должно быть верным. Оно считается действительным при любом значении с . Результат деления 0 на 0 принимается любое значение. Для уменьшения многозадачности данный вариант не рассматривается.
Проверка результата деления целых чисел
Проверку осуществляют умножением. Чтобы произвести проверку деления, нужно полученное частное умножить на делитель, если в результате получается число, равное делимому, тогда результат считается правильным.
Рассмотрим на примере решение с проверкой результата.
Результат деления 72 на — 9 равен — 7 . Произвести проверку данного выражения.
Решение
Выполняем проверку деления. Необходимо произвести умножение полученного частного и делителя, то есть ( − 7 ) · ( − 9 ) = 63 . Проверка показала, что 63 отлично от 72 , значит действие выполнено неверно.
Деление многочленов столбиком
Алгоритм деления в столбик применяется в частности при нахождении интегралов.
- Решение онлайн
- Видеоинструкция
Пример деления в столбик . Найти частное деления и остаток многочлена:
№1.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 |
| -9x 2 -42 |
№2.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 -9x |
| -9x 2 -42 | |
| -9x 2 + 27x | |
| -27x -42 |
№3.
| x 3 -12x 2 -42 | x -3 |
| x 3 -3x 2 | x 2 -9x -27 |
| -9x 2 -42 | |
| -9x 2 + 27x | |
| -27x -42 | |
| -27x + 81 | |
| -123 |
Целая часть: x 2 -9x -27
Остаток: -123
Таким образом, ответ можно записать как:
см. также и другие примеры решение столбиком.
Пример №1 . Найти частное и остаток от деления многочлена на многочлен:
P(x)=2x 5 +3x 3 -x 2 +4x+1, Q(x)=2x 2 -x+1
Пример №2 . Не производя деление найти остаток от деления многочлена на двучлен:
P(x)=-x 4 +6x 3 -2x 2 +x-2, Q(x)=x-6
Решение. Выделим общий множитель (x-6).
-x 3 (x-6)-2x(x-6)-12x+x-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-66-2 = -x 3 (x-6)-2x(x-6)-11(x-6)-68
Остаток от деления: -68/(x-6)
http://zaochnik.com/spravochnik/matematika/dejstvitelnye-ratsionalnye-irratsionalnye-chisla/delenie-tselyh-chisel/
http://math.semestr.ru/gauss/factor.php