Уравнение диффузии граничные условия неймана

Численные методы решения уравнений эллиптического типа

Введение

Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

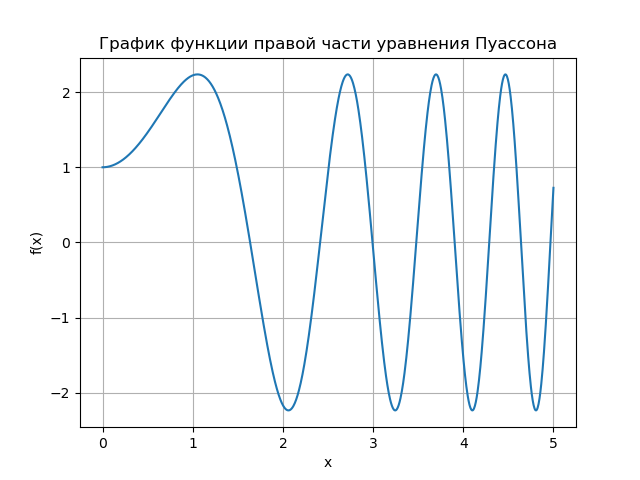
Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

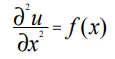
Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

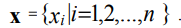
Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

(5)

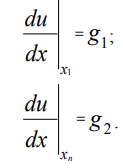
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

(6)

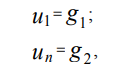
где u1, un – значения функции u(x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

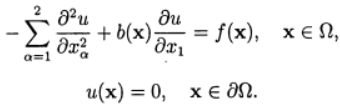
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

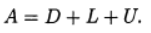
Метод релаксации соответствует использованию итерационного метода:

(11)

При \ говорят о верхней релаксации, при — о нижней релаксации.

На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
2. Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

1. Рындин Е.А. Методы решения задач математической физики. – Таганрог:
   Изд-во ТРТУ, 2003. – 120 с.
2. Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
   «ЛИБРОКОМ», 2010. — 320 с.

Краевые задачи теории диффузии

Дифференциальное уравнение диффузии, выведенное на основе общих законов физики, устанавливает связь между временным и пространственным изменением концентрации в любой точке тела, в которой происходит диффузионный процесс. Дифференциальное уравнение диффузии имеет бесконечное множество решений. Чтобы из этого множества выбрать решение, характеризующее конкретный рассматриваемый процесс, и дать полное математическое описание процесса, необходимо к основному дифференциальному уравнению присоединить дополнительные условия, включающие геометрические, физические и краевые условия.

Геометрические условия определяют форму и линейные размеры тела.

Физические условия определяют физические параметры: коэффициент диффузии,

константу растворимости, объемную плотность потока диффузанта.

Краевыми условиями называют совокупность начального и граничного условий. Начальные условия задаются только при изучении нестационарных процессов и состоят в задании распределения концентрации внутри тела в момент времени, выбранный за начальный. Граничные условия отображают условия диффузионного взаимодействия между окружающей средой и поверхностью тела.

Граничные условия для изучаемой задачи могут быть заданы несколькими способами; в теории диффузии различают граничные условия I, II, III, IV родов. (Граничные условия IV рода иначе называют условиями сопряжения). Следует помнить, что число граничных условий превышает число границ. Так, в задаче по дегазации шарика (одномерный случай), необходимо задать условия как на внешней поверхности шарика, так и в центре. Часто граничные условия задаются «на бесконечности».

Граничные условия 1-го рода

В граничных условиях I – рода задается распределения концентрации диффузанта по поверхности Σ тела, как функция координат и времени.

В частном случае концентрация на поверхности – функция только времени

При наличии двух плоскостей (как это имеет место в методе газопроницаемости) задаются

две функции изменения концентрации диффузанта на входе в образец (например, пластину толщиной Н). Тогда граничные условия первого рода принимают вид:

Подобный режим в теории диффузии обозначается как граничная задача I-I.

В более простом случае – концентрация постоянна (условие Дирихле).

Если концентрация на границе в процессе эксперимента поддерживается равной нулю, то

вводится понятие поглощающей стенки.

Типичным примером, в котором на различных границах поддерживаются различные

варианты граничных условий первого рода, является случай проницаемости плоской мембраны толщиной Н. Здесь С(0,t)=C0, C(H,t)=0.

Условия 2-го рода

В условиях II – рода задается распределение плотности потока диффузанта для каждой точки поверхности как функция координат и времени

j = −D ∂C

где n — внутренняя нормаль к поверхности Σ.

Если поток за поверхности зависит от координаты, но не зависит от времени, граничное условие называется условием Неймана.

Важным частным случаем является отражающая стенка (отсутствие потока через внешние

поверхности образца – условие диффузионной изоляции):

В последнем случае граничная поверхность изолирована (диффузия через нее невозможна,

поток диффузанта через такую границу равен нулю).

Если образец имеет две границы (например, тонкая пластина), то в зависимости от условий на его внешних поверхностях различают граничные задачи II-II, I-II и II-I.

В центре шарика (сферы) поток отсутствует, следовательно, в центре – граничное условие

II-го рода (на поверхности I-го рода).

4.3 Условия 3-го рода

В граничных условиях III – рода задают закон конвективного массообмена между поверхностью тела и окружающей средой.

∂n Σ

– концентрация на поверхности; Cc

– концентрация примеси в окружающей среде, ks –

коэффициент пропорциональности, характеризующий интенсивность концентрационного взаимодействия среды с заданной концентрацией диффузанта Сс с поверхностью тела. В нестационарных процессах концентрация диффузанта в окружающей среде в общем случае изменяется во времени.

В этом случае на поверхности тела задается плотность потока диффузанта, возникающего из-за разности концентраций диффузанта на поверхности тела и в окружающей среде.

Ур.36 является аналитическим выражением граничного условия III рода, которое широко применяется при аналитических исследованиях массо-переноса в твердых телах, обтекаемых потоками жидкости или газа на границе между телом и флюидом.

Уравнение для упругой стенки полностью идентично уравнению Ньютона для теплообмена лучеиспусканием. Оно подразумевает, что концентрация не мгновенно устанавливается на поверхности, а в процессе некоторого времени, т.е. граница оказывает сопротивление диффузионному потоку (иногда более сильное, чем собственно диффузия). В этом случае поток не является постоянным, а изменяется как разность между концентрациями в твердом теле и в окружающем объеме.

Приведем вывод выражения для упругой стенки.

При справедливости закона Генри можно записать следующие выражения для потоков на поверхности твердого тела:

j1 = −k1C1x=0 →

поток газа из твердого тела;

поток из газа в твердое тело,

где k1 – константа дегазации; k2 – константа насыщения.

Если бы установилось равновесие, то

В нашем случае равновесия нет и

Внешний поток: k 2 p − k1C x=0 =

внут ∂x

x=0

jвнеш – т.к. нет накопления примеси на поверхности раздела фаз.

− D ∂C

D ∂C

x=0

Мы получили выражение, идентичное общему случаю.

= −

∂ ⎛ ⎞

Граничные условия III-го рода представляют собой общий случай. Из него может быть

получены выражения для условий I-го и II-го рода.

– условие I-го рода (закон

⎛ ⎞

Генри). При k = 0 , граничное условие II-го рода.

При сорбции C x=0 Cравн .

Граничные условия 3-го рода можно разделить на три категории: 1) Линейные; 2)

Нелинейные; 3) Нестационарные. Следует отметить, что наличие на поверхности (поверхностях) образца сложных химических процессов, в том числе — сопровождающихся выделением или поглощением тепла, приводит к граничным условиям 3-го рода весьма сложного вида.

В общем виде, при исследовании процессов диффузии в двустороннем образце возможно возникновение различных граничных задач: I-I, II-II, III-III, I-II, II-I, I-III, III-I, II-III, III-II, что может существенно затруднить обработку и интерпретацию данных диффузионных экспериментов.

К счастью, на практике часто встречаются согласованные (однородные нулевые)

CΣ = 0 – поглощающая стенка;

∂C

= 0 – отражающая стенка;

∂C + hC

= 0 – упругая стенка.

В первой части Курса лекций мы будем оперировать именно ими.

Условия 4-го рода

Граничные условия сопряжения (IV–рода) соответствуют массообмену поверхности тела с окружающей средой или массообмену соприкасающихся твердых тел, когда концентрация на соприкасающихся поверхностях одинакова (в случае газообразного диффузанта подчиняется закону Генри). Задаются они в виде

− D ∂C1

∂n

где Кр1 и Кр2 – константы растворимости, а D1 и D2 – коэффициенты диффузии диффузанта в

соприкасающихся средах 1 и 2, соответственно.

к поверхности раздела.

∂ означает дифференцирование вдоль нормали

Первое равенство выражает условие непрерывности концентрационного поля, а второе – закон сохранения энергии на поверхности соприкосновения двух сред (или тел) — Потоки на границе должны быть равны друг другу.

В отличие от случая теплопроводности где разрыва температуры на границе раздела фаз нет, в диффузии на границе раздела твердых тел возможны разрывы концентраций. Лишь в частном случае, при равенстве констант растворимости диффузанта в обеих фазах (при

Kp1 = K p2 ), то в точке

C1 = C2 и разрыва в концентрационном поле на границе фаз нет.

Граничные условия. Задачи Дирихле и Неймана

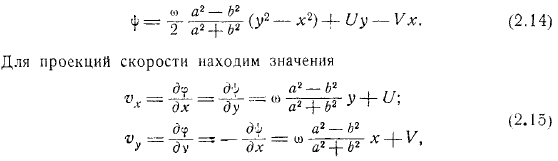
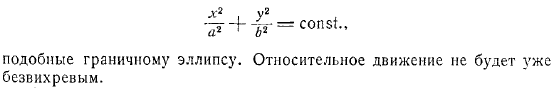
Граничные условия. Задачи Дирихле и Неймана

Поиск комплексного потенциала, определяющего планарное невращательное движение несжимаемой жидкости гидромеханики, можно свести к поиску функции потока, поскольку потенциал связан с известными условиями Коши. Римана, из известной функции можно определить в виде квадратуры. Функция потока, которая считается непрерывной во всех точках течения несжимаемой жидкости, удовлетворяет уравнению Лапласа в этих точках, а на определенных границах течения-некоторым известным условиям. Формат зависит от реализации квартиры.

Показаны простейшие случаи, без цели исчерпывающей классификации различных типов граничных условий. Рассматривая плоское течение бесконечно статичной бесконечной жидкости о движении тела в идеальной жидкости, возникающее при движении цилиндра, граничные условия для функции потока однозначно следующие — поскольку скорость в этих точках должна быть равна нулю. В каждой точке контура движущегося тела, нормальная проекция скорости должны совпадать.

• Угол между элементом линии потока и осью, а соотношение между позволяет выразить рассматриваемое условие. И если в жидкости еще есть неподвижный объект, то по их контуру понятно, что обычная составляющая скорости соседних частиц жидкости должна быть равна нулю, другими словами, сам неподвижный контур должен находиться в контакте с текущей линией. В этом случае необходимо добавить граничное условие к предыдущему условию. Для точки фиксированного контура.

Если тело движется поступательно со скоростью, направленной вдоль оси, то условие равно. Принять форму, или все точки контура, после того как цилиндрический объект совершает какое-либо движение. При наличии поступательного потока с бесконечно большой скоростью расстояние до удаленной точки равно, ориентированной вдоль оси и обтекающей неподвижный объект. Граничное условие, очевидно, выглядит так: для бесконечности показанные нами граничные условия в основном используются при исследовании стационарного движения, но остаются справедливыми для нестационарного потенциала.

В этом случае предыдущее выражение вводит только время в качестве параметра. Параметры зависят от. Известное значение функции на контуре области называется задачей Дирихле, хотя это задача определения функции, удовлетворяющей уравнению Лапласа в области. Таким образом, мы видим, что определение плоского невращательного движения несжимаемой жидкости, вызванного движением контура, ограничивающего область течения, приводит к решению конкретной задачи Дирихле.

При решении гидродинамических задач можно также сначала найти все потенциалы скорости. Он также должен удовлетворять уравнению Лапласа в области течения. Но является ли граничное условие схемы необходимым для функции? Другой само определение потенциала скорости является вертикальной проекцией в скорости частицы жидкости, прилегающие к контуру, и, следовательно, граничное условие для функции принимает форму an является нормальной проекции скорости точки контура. В частности, в терминах фиксированных границ, мы получим условие.

Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. Людмила Фирмаль

В области, задача определения функции, которая удовлетворяет уравнению Лапласа по известному значению нормальной производной функции на контур области называется задачей Неймана. Поэтому гидродинамические задачи приводят к решению некоторых задач Неймана. Вы можете использовать функцию для определения функции и наоборот. Поэтому ясно, что задача Неймана может быть сведена к задаче Дирихле, или наоборот. Факт, запомните состояние Коши-Римана и проследите за цифрой некоторое время.

Направление нормали в направлении оси, и направление касательной в направлении оси, получаем следующие соотношения сразу, вы можете перейти к задаче Неймана из задачи Дирихле, если есть проблема Неймана, то есть, если вы знаете значение на схеме, это будет следующим образом. Переходим к границе области течения, и поэтому Дирихле. В случае задачи многосвязной области с границей на контуре предыдущее выражение отображает значение аддитивной постоянной для каждой схемы. По значению одной из этих аддитивных констант движение определяется значением производной функции, поэтому его можно выбрать.

Любые константы в будут отображаться. Дана циркуляция скоростей по контуру, которые неприводимы друг к другу. Это полностью совпадает с замечанием о том, что вращательные движения, сделанные в конце раздела главы движение кругового цилиндра , полностью определяются задачей. И цикл только в том случае, если настройка циклическая. В качестве простого примера рассмотрим задачу о невращательном движении несжимаемой жидкости, заключенной в эллиптический цилиндр. Пусть эллиптическое уравнение.

• Его движение характеризуется проекцией на координатную ось скорости и угла поворота скорости его центра. Тогда функция потока должна удовлетворять уравнению в эллипсе и граничному условию самого эллипса. Полином порядка. Я ищу функцию в виде. Уравнение представляет собой отношение. Уравнение из условия является результатом. Это означает связь между для проекции скорости найдите значение, вы можете получить оттуда легко.

Простейший случай чистого поступательного движения цилиндра, когда, выглядит так: то есть жидкость движется вместе со всем цилиндром. Для чистого вращения, когда, это выглядит так: линия потока абсолютного движения гиперболическая. Подчеркнем, что полученная нами формула определяет абсолютное движение жидкости, но относится к движущимся координатным осям.

Движение жидкости относительно этих движущихся координатных осей определяется вычитанием проекции переносной скорости из проекции абсолютной скорости. В результате проекция относительной скорости выглядит следующим образом и представляет собой эллипс, аналогичный граничному эллипсу. Относительное движение больше не является вихревым.

В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института