Уравнение диффузии метод конечных разностей

Диффузия

Три разных подхода к моделированию диффузии. Рассматриваем одномерное уравнение.

Метод конечных разностей

Однако не все так просто! Численное решение дифференциальных уравнений в частных производных чревато «опасностями», например, если мы зададим N = 10, то получим явно неправдоподобный результат, т.е столкнемся с т.н. неустойчивостью численного метода. Но подробности оставим курсу «Численные методы».

Метод клеточных автоматов

А здесь даже уравнение писать не нужно. В первый момент времени примесь есть только в центральной ячейке. Концентрация примеси в ячейке на следующем шаге частью остается в самой ячейке, частью переходит в соседние — правую и левую. Если течения нет, то эти доли одинаковы — по 1/3.

Мы можем усовершенствовать нашу модель, если введем течение. Тогда доли L, S и R изменятся. Например, если течение направлено вправо, то они могут быть 1/10, 3/10 и 6/10 соответственно. В дифференциальном уравнении этого можно было бы добиться, делая переменным коэффициент диффузии. Правда тогда придется переделать и разностное уравнение.

Заметьте, что концы трубы в программе исключены из рассмотрения ( x = 2:ncells-1; ). Чтобы рассмотреть их, нужно с помощью условного оператора проверять, достигнут ли конец трубы. Тогда можно сделать концы, например, отражающими, т.е. частицы будут отскакивать от них вглубь трубы.

Источник можно задавать разовой концентрации (как в примере), а можно постоянной. Можно задавать перемещение источника вдоль трубы.

Модель очевидно обобщается на 2-х и 3-х мерный случаи, только количество соседей станет больше. Тогда в ней можно вводить препятствия различных видов (модель распространения загрязнения с домами и лесом).

Вспомнив, про то, что движение каждой частицы примеси происходит случайным образом, мы можем применить для моделирования ее перемещений.

Метод Монте-Карло

Частица может на каждом шаге двинуться вправо, влево или остаться на месте. Через некоторое время (количество шагов) она окажется на каком-то расстоянии от исходной точки. Если запустить множество частиц и позволить им всем двигаться по одинаковым законам (вправо, влево или стоять), а через некоторое время посмотреть, сколько из них удалились на то или иное расстояние от источника, то мы и получим распределение концентраций (количество части в единице объема).

Читайте также

Комментарии

Дмитрий Храмов
Компьютерное моделирование и все, что с ним связано: сбор данных, их анализ, разработка математических моделей, софт для моделирования, визуализации и оформления публикаций. Ну и за жизнь немного.

Численные методы решения уравнений эллиптического типа

Введение

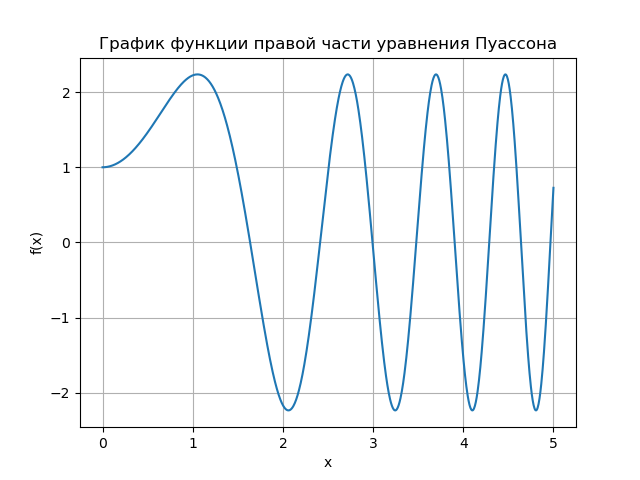
Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.

Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения опреде­ляется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.

Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

(1)

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.

Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:

(2)

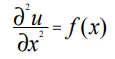
Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:

(3)

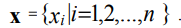
Граничные условия первого рода (условия Дирихле) для рассматривае­мой задачи могут быть представлены в виде:

(4)

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.

Граничные условия второго рода (условия Неймана) для рассматривае­мой задачи могут быть представлены в виде:

(5)

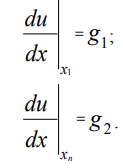
Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, по­лучим:

(6)

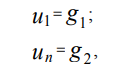
где u1, un – значения функции u(x) в точках x1, xn соответственно.

Проводя дискретизацию граничных условий Неймана на сетке (3), по­лучим:

(7)

Проводя дискретизацию уравнения (2) для внутренних точек сетки, по­лучим:

(8)

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.

Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].

Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).

Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:

Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии

(9)

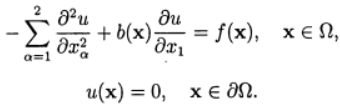
Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

(10)

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:

(10)

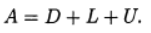
Метод релаксации соответствует использованию итерационного метода:

(11)

При \ говорят о верхней релаксации, при — о нижней релаксации.

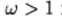
На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при .

1. Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
2. Показано что метод релаксации имеет оптимальный диапазон () параметра релаксации.

Ссылки:

1. Рындин Е.А. Методы решения задач математической физики. – Таганрог:
   Изд-во ТРТУ, 2003. – 120 с.
2. Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
   «ЛИБРОКОМ», 2010. — 320 с.