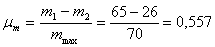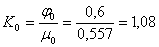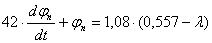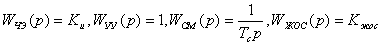Уравнение динамики соответствует объекту регулирования
3.1. Динамический режим САУ.
Уравнение динамики
Установившийся режим не является характерным для САУ. Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от заданной величины.
Процесс установления требуемого значения управляемой величины называется регулированием . Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.
Рассмотрим САР, находящуюся в установившемся режиме, характеризующемся значением выходной величины y = y o . Пусть в момент t = 0 на объект воздействовал какой — либо возмущающий фактор, отклонив значение регулируемой величины. Через некоторое время регулятор вернет САР к первоначальному состоянию (с учетом статической точности) (рис.24). Если регулируемая величина изменяется во времени по апериодическому закону, то процесс регулирования называется апериодическим .
При резких возмущениях возможен колебательный затухающий процесс (рис.25а). Существует и такая вероятность, что после некоторого времени Т р в системе установятся незатухающие колебания регулируемой величины — незатухающий колебательный процесс (рис.25б). Последний вид — расходящийся колебательный процесс (рис.25в).
Таким образом, основным режимом работы САУ считается динамический режим , характеризующийся протеканием в ней переходных процессов . Поэтому второй основной задачей при разработке САУ является анализ динамических режимов работы САУ .
Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамики y(t) = F(u,f,t) , описывающее изменение величин во времени. Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования САУ в динамических режимах является метод решения дифференциальных уравнений . Порядок дифференциальных уравнений может быть довольно высоким, то есть зависимостью связаны как сами входные и выходные величины u(t), f(t), y(t) , так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:
F(y, y’, y”. y (n) , u, u’, u”. u (m) , f, f ’, f ”. f (k) ) = 0 .
3.2. Линеаризация уравнения динамики
В общем случае уравнение динамики оказывается нелинейным, так как реальные звенья САУ обычно нелинейны. В целях упрощения теории нелинейные уравнения заменяют линейными, которые приблизительно описывают динамические процессы в САУ. Получаемая при этом точность уравнений оказывается достаточной для технических задач. Процесс преобразования нелинейных уравнений в линейные называется линеаризацией уравнений динамики . Рассмотрим сначала геометрическое обоснование линеаризации.
В нормально функционирующей САУ значение регулируемой и всех промежуточных величин незначительно отличается от требуемых. В пределах малых отклонений все нелинейные зависимости между величинами, входящими уравнение динамики, могут быть приближенно представлены отрезками прямых линий. Например, нелинейная статическая характеристика звена на участке АВ (рис.26) может быть представлена отрезком касательной в точке номинального режима А»В». Начало координат переносится в точку О’, и в уравнениях записываются не абсолютные значения величин y,u,f , а их отклонения от номинальных значений: 



Математическое обоснование линеаризации состоит в том, что если известно значение f(a) какой — либо функции f(x) в любой точке x = a , а также значения производных от этой функции в данной точке f’(a), f”(a), . f (n) (a) , то в любой другой достаточно близкой точке x + 
Аналогично можно разложить и функцию нескольких переменных. Для простоты возьмем упрощенный, но наиболее характерный вариант уравнения динамики САУ: F(y,y’,y»,u,u’) = f. Здесь производные по времени u’,y’,y» также являются переменными. В точке, близкой к номинальному режиму: f = f н + 


В номинальном режиме, когда все отклонения и их производные по времени равны нулю, получаем частное решение уравнения: F н = f н . Учитывая это и вводя обозначения получим:
a o 





Отбрасывая все знаки 
a o y” + a 1 y’ + a 2 y = b o u’ + b 1 u + c o f .
Отбрасывая все знаки 
В более общем случае:
a o y (n) + a 1 y (n-1) + . + a n — 1 y’ + a n y = b o u (m) + . + b m — 1u’ + b m u + c o f.
При этом всегда нужно помнить, что в данном уравнении используются не абсолютные значения величин y, u, f их производных по времени, а отклонения этих величин от номинальных значений. Поэтому полученное уравнение будем называть уравнением в отклонениях .
К линеаризованной САУ можно применить принцип суперпозиции : реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет звено с двумя входами u и f разложить на два звена, каждое из которых имеет один вход и один выход (рис.27). Поэтому в дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид:
a o y (n) + a 1 y (n-1) + . + a n — 1 y’ + a n y = b o u (m) + . + b m — 1u’ + b m u.
Это уравнение описывает САУ в динамическом режиме лишь приближенно с той точностью, которую дает линеаризация. Однако следует помнить, что линеаризация возможна только при достаточно малых отклонениях величин и при отсутствии разрывов в функции F в окрестностях интересующей нас точки, которые могут быть созданы различными выключателями, реле и т.п.
Обычно n 
3.3. Передаточная функция
В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора p = d/dt так, что, dy/dt = py , а p n = d n /dt n . Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p . В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:
a o p (n) y + a 1 p (n-1) y + . + a n y = (a o p (n) + a 1 p (n-1) + . + a n )y = (b o p (m) + b 1 p (m-1) + . + b m )u
Не надо путать эту форму записи с операционным исчислением хотя бы потому, что здесь используются непосредственно функции времени y(t), u(t) ( оригиналы ), а не их изображения Y(p), U(p) , получаемые из оригиналов по формуле преобразования Лапласа. Вместе с тем при нулевых начальных условиях с точностью до обозначений записи действительно очень похожи. Это сходство лежит в природе дифференциальных уравнений. Поэтому некоторые правила операционного исчисления применимы к операторной форме записи уравнения динамики. Так оператор p можно рассматривать в качестве сомножителя без права перестановки, то есть py
Поэтому уравнение динамики можно записать также в виде:
Дифференциальный оператор W(p) называют передаточной функцией . Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t) , поэтому ее еще называют динамическим коэффициентом усиления . В установившемся режиме d/dt = 0 , то есть p = 0 , поэтому передаточная функция превращается в коэффициент передачи звена K = b m /a n .
Знаменатель передаточной функции D(p) = a o p n + a 1 p n — 1 + a 2 p n — 2 + . + a n называют характеристическим полиномом . Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции .
Числитель K(p) = b o p m + b 1 p m — 1 + . + b m называют операторным коэффициентом передачи . Его корни, при которых K(p) = 0 и W(p) = 0 , называются нулями передаточной функции .
Звено САУ с известной передаточной функцией называется динамическим звеном . Оно изображается прямоугольником, внутри которого записывается выражение передаточной функции. То есть это обычное функциональное звено, функция которого задана математической зависимостью выходной величины от входной в динамическом режиме. Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция W и (p) = 1/p . Схема САУ, составленная из динамических звеньев, называется структурной .
3.4. Элементарные динамические звенья
Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями . Передаточная функция элементарного звена в общем виде задается отношением двух полиномов не более чем второй степени:
Wэ(p) = 
Известно также, что любой полином произвольного порядка можно разложить на простые сомножители не более, чем второго порядка. Так по теореме Виета можно записать
D(p) = a o p n + a 1 p n — 1 + a 2 p n — 2 + . + a n = a o (p — p 1 )(p — p 2 ). (p — p n ),
где p 1 , p 2 , . p n — корни полинома D(p) . Аналогично
K(p) = b o p m + b 1 p m — 1 + . + b m = b o (p — p
m — корни полинома K(p) . То есть
Корни любого полинома могут быть либо вещественными p i = a i , либо комплексными попарно сопряженными p i = a i ± j 
(p — a i + j 



Поэтому любую сложную передаточную функцию линеаризованной САУ можно представить как произведение передаточных функций элементарных звеньев. Каждому такому звену в реальной САУ, как правило, соответствует какой — то отдельный узел. Зная свойства отдельных звеньев можно судить о динамики САУ в целом.
В теории удобно ограничиться рассмотрением типовых звеньев , передаточные функции которых имеют числитель или знаменатель, равный единице, то есть W(p) = 

- Какой режим САУ называется динамическим?
- Что называется регулированием?
- Назовите возможные виды переходных процессов в САУ. Какие из них являются допустимыми для нормальной работы САУ?
- Что называется уравнением динамики? Каков его вид?
- Как провести теоретическое исследование динамики САУ?
- Что называется линеаризацией?
- В чем геометрический смысл линеаризации?
- В чем состоит математическое обоснование линеаризации?
- Почему уравнение динамики САУ называется уравнением в отклонениях?
- Справедлив ли для уравнения динамики САУ принцип суперпозиции? Почему?
- Как звено с двумя и более входами представить схемой, состоящей из звеньев с одним входом?
- Запишите линеаризованное уравнение динамики в обычной и в операторной формах?
- В чем смысл и какими свойствами обладает дифференциальный оператор p?
- Что называется передаточной функцией звена?
- Запишите линеаризованное уравнение динамики с использованием передаточной функции. Справедлива ли эта запись при ненулевых начальных условиях? Почему?
- Напишите выражение для передаточной функции звена по известному линеаризованному уравнению динамики: (0.1p + 1)py(t) = 100u(t).
- Что называется динамическим коэффициентом усиления звена?
- Что называется характеристическим полиномом звена?
- Что называется нулями и полюсами передаточной функции?
- Что называется динамическим звеном?
- Что называется структурной схемой САУ?
- Что называется элементарными и типовыми динамическими звеньями?
- Как сложную передаточную функцию разложить на передаточные функции типовых звеньев?
Динамические свойства объекта, кривая разгона которого имеет вид
Передаточная функция для структурной схемы соединения звеньев – формула


















Таблица Гурвица соответствует системе регулирования 3-го порядка


Расположение корней характеристического уравнения соответствует системе управления




. — способность системы автоматического управления самостоятельно возвращаться в состояние равновесия после устранения возмущающего воздействия. Устойчивость
При показанном на рисунке расположении на комплексной плоскости корней характеристического уравнения система регулирования







Уравнение динамики соответствует объекту регулирования 




Кривая разгона объекта регулирования


_______ — зависимость выходной величины объекта регулирования от времени при ступенчатом изменении его входной величины, отличающемся от единичного. кривая разгона
Кривая разгона соответствует объекту регулирования





Отношение постоянных времени – кривая разгона:


. . объекта — время, в течение которого выходная величина устойчивого объекта, изменяясь с постоянной начальной скоростью, достигает нового установившегося значения. постоянная времени
. — это интервал времени между моментом изменения входной величины объекта и началом изменения его выходной величины.
. — способность объекта самостоятельно приходить в новое состояние равновесия после нанесения возмущающего воздействия. самовыравнивание
. — способность объекта накапливать или сохранять вещество или энергию. Емкость
Динамические свойства объекта, кривая разгона которого имеет вид





Для объектов регулирования, кривые разгона которых приведены на рисунке, соблюдается следующее соотношение между их степенью самовыравнивания р и емкостью С:




Дифференцирования — пропорционально-дифференциального регулятора с независимыми параметрами настройки
Предварения — пропорционально-дифференциального регулятора с зависимыми параметрами настройки
Статическая ошибка регулирования всегда присутствует в системах регулирования с _______ регулятором
Статическая ошибка регулирования всегда отсутствует в системах регулирования с _______ регулятором
Разность между новым установившимся значением регулируемой величины и ее заданным значением представляет собой
статическую ошибку регулирования
Максимальное отклонение регулируемой величины в переходном процессе от ее заданного значения представляет собой
динамическую ошибку регулирования
Выраженное в процентах отношение второй х2 и первой x1 амплитуд колебаний регулируемой величины во время переходного процесса представляет собой
Квадрат площади между кривой переходного процесса и новым установившимся значением регулируемой величины представляет собой
интегральную квадратичную ошибку регулирования
. . — это интервал времени, в течение которого, начиная от момента приложения типового воздействия на систему, регулируемая величина достигает нового равновесного значения с некоторой заранее установленной точностью.
Статическая ошибка регулирования возникает в одноконтурной системе, состоящей из объекта с положительным самовыравниванием и
Автоколебания возникают в одноконтурной системе, состоящей из объекта с положительным самовыравниванием и _______ регулятора
Определение коэффициентов уравнения динамики объекта регулирования
6. Определение коэффициентов уравнения динамики объекта регулирования
Существует два метода определения коэффициентов уравнения динамики объекта регулирования: аналитический и графоаналитический. Первый из них связан с определением конструктивных и теплотехнических характеристик, что порой бывает порой затруднительно в судовых условиях и к тому же требует много времени на обработку полученных данных. Второй метод более прижился в инженерной практике, прост в использовании и экономный во времени. Заключается он в снятии разгонной характеристики по каналу регулирования путём нанесения ступенчатого возмущения на объект регулирования. При съёме разгонной характеристики систему автоматического регулирования размыкают, т. е. объект отсоединяют от регулятора. Возмущение обычно наносится регулирующим органом (РО), в данной курсовой работе роль регулирующего органа выполняет регулирующий топливный клапан, путём изменения его положения на небольшую величину. Эта величина возмущения выбирается так, чтобы изменение выходного параметра не выходило за технологически допустимую величину. В нашем случае величина возмущающего воздействия (ступенчатого открытия топливного клапана) составляет:
Если объект является неустойчивым или нейтральным, то снимают часть разгонной характеристики с допустимыми отклонениями выходной величины. Для регистрации величины отклонения регулируемого параметра используют безинерционные точные измерительные приборы, самописцы, шлейфовые или запоминающие осциллографы. При ручной регистрации разгонной характеристики снимают показания измерительного прибора через равные промежутки времени ∆t. По заданию курсовой работы:
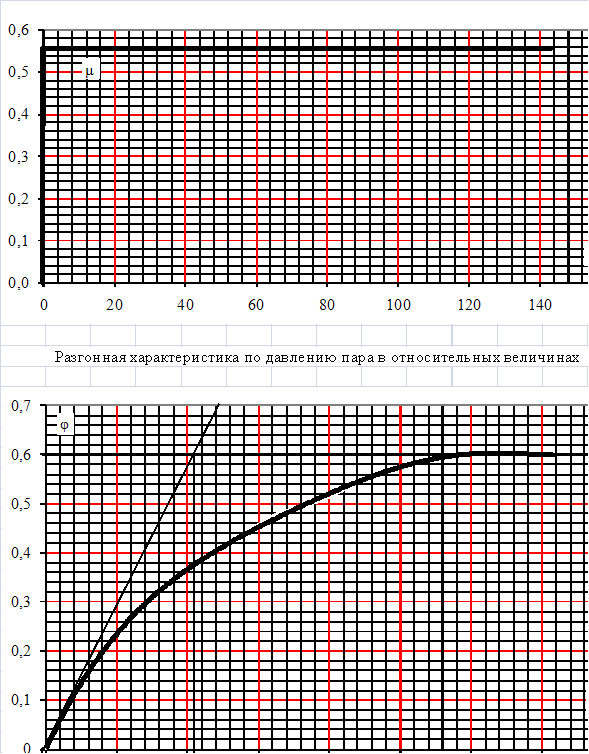
Для определения постоянной времени объекта регулирования на разгонной характеристике проводим из точки начала координат касательную к кривой. Доведя касательную до уровня (линии) установившегося состояния, получаем точку пересечения. Из этой точки к оси времени проводим перпендикуляр. Расстояние от начала кривой разгонной характеристики до точки пересечения перпендикуляра с осью времени будет постоянной времени, величина которого в нашем варианте имеет вид:
С разгонной характеристики также определяем
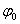
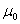
Отсюда по известной формуле определяем коэффициент усиления объекта
С учётом выше написанного запишем типовое уравнение динамики котла как объекта регулирования по давлению пара:
Переходная характеристика объекта регулирования
1. Выбор регулятора. Принципиальная, функциональная и структурная схемы регулятора. Устройство и принцип действия регулятора и его элементов
Основная регулируемая величина — давление пара, которая характеризует баланс между производимым паром в котле и потребляемым. Нарушение этого баланса сопровождается отклонением давления, которое измеряется регулятором давления пара, изменяющим через исполнительный орган подачу топлива в топку и восстанавливающим тем самым нарушенный тепловой баланс.
Основные требования к регулятору давления пара могут быть сформулированы следующим образом:
-отклонение давление пара в точке отбора импульса на регулятор должно составлять ±0.05 МПа;
-в переходных режимах падение давления пара не должно превышать 10% номинального при изменении нагрузки котла от минимальной до максимальной за период не менее 60с;
-допускается повышение давления пара, не приводящее к подрыву предохранительных клапанов при изменении нагрузки котла от максимальной до минимальной за время не менее 30с;
-давление пара в указанных пределах должно поддерживаться при изменениях расхода пара со скоростью не более 1.5% в секунду (при повышении нагрузки) и 3% в секунду (при снижении нагрузки).
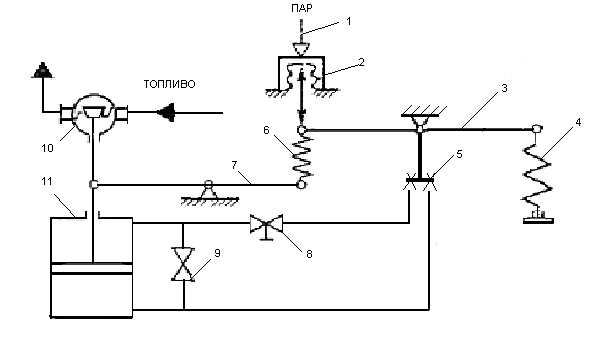
Рис. 2.1.1. Принципиальная схема П-регулятора давления пара
Котел обладает малым самовыравниванием по давлению пара, поэтому регуляторы давления пара должны обязательно иметь стабилизирующие элементы. Для регулирования давления пара обычно применяют 1- и 2-импульсные П-регуляторы, а также ПИ-регуляторы.
Для судов отечественной постройки типичен гидравлический П-регулятор давления пара с жесткой обратной связью (рис.2.1). Регулятор измеряет давление в паропроводе посредством сильфона 2, к которому подведен импульсный трубопровод 1. В установившемся режиме усилие от сильфона уравновешивается натяжениями задающей пружины 4 и пружины обратной связи 6, заслонка водяного усилительного реле 5 (к нему подведена вода под давлением) находится в среднем положении, и поршень ИМ 10 неподвижен. При отклонении давления пара от заданного равновесие нарушается, новое усилие сильфона 2 на рычаг 3 приводит к отклонению заслонки регулирующего реле 5 и подаче воды в одну из полостей ИМ 10; в результате его поршень перемещается и изменяет степень открытия регулирующего подачу топлива клапана 11, оказывая регулирующее воздействие на давление пара в котле. Одновременно шток клапана 11 через рычаг 7 и пружину обратной связи 6 оказывает выключающее воздействие на усилительное реле 5. Дроссельный клапан 8 предназначен для изменения времени ИМ, а клапан 9 — для соединения его полостей при переходе с автоматического регулирования на ручное.
Для незначительного изменения давления в пароводяном коллекторе котла место отбора импульса выбирают в паропроводе за стопорным клапаном котла. При этом давление в пароводяном коллекторе, по сравнению с давлением в месте отбора импульса будет выше на значение снижения давления, вызванного гидравлическими сопротивлениями паропровода от коллектора до места отбора импульса. Для повышения запаса устойчивости АСР необходимо увеличивать неравномерность регулирования DРмах, т. е. наклон статической характеристики, которая определяется в основном жесткостью пружины обратной связи.
Место отбора импульса по длине паропровода следует выбирать таким образом, чтобы гидравлические потери от коллектора до этого места компенсировали неравномерность статической характеристики, обусловленную ЖОС. Для обеспечения запаса устойчивости значение DРмах должно составлять 10—15% номинального регулируемого давления. Так как малые нагрузки котла по сравнению с большими характеризуются меньшим коэффициентом самовыравнивания по давлению пара, то на малых нагрузках для создания достаточного запаса устойчивости целесообразно иметь больший угол наклона статической характеристики.
При своей простоте П-регуляторы давления пара требуют для обеспечения устойчивости относительно большого коэффициента обратной связи. Жесткая обратная связь в них осуществляется по положению топливорегулирующего органа или от расходомера топлива и не учитывает такие факторы, как элементарный состав топлива и его плотность, износы топливорегулирующего органа и распылителей форсунок, вследствие чего при одинаковых нагрузках котла значение сигнала обратной связи может быть различным. Это приводит к отклонению давления пара от заданной статической характеристики.
По приведенной выше принципиальной схеме построим функциональную схему:
Рис. 2.1.2. Функциональная схема П-регулятора
ЧЭ – чувствительный элемент;
УУ – усилительное устройство;
ИМ – исполнитель-ный механизм;
ЖОС – жесткая обратная связь
Тогда структурная схема примет вид:
Рис. 2.1.3. Структурная схема П-регулятора
Передаточные функции звеньев:
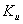
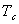
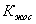
http://poisk-ru.ru/s39007t12.html
http://kazedu.com/referat/197980/2