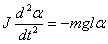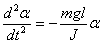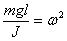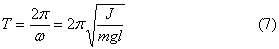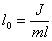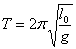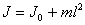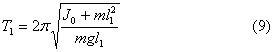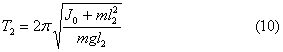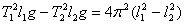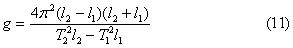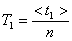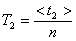Уравнение динамики вращательного движения физического маятника
Лабораторная работа № 112
Цель работы: Экспериментальное определение ускорения свободного падения методом колебания физического маятника. Определение момента инерции физического маятника.
Приборы и принадлежности: универсальный маятник ФП-1, секундомер, линейка.
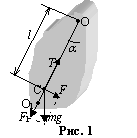
В теории колебаний физическим маятником называется твердое тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр масс и способное совершать колебания относительно этой оси (рис.1).
 |
Можно показать, что маятник, отклоненный на малый угол a от положения равновесия, будет совершать гармонические колебания.
Обозначим через J момент инерции маятника относительно оси О. Пусть точка С является центром масс. Силу тяжести 
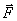
Для малых углов sin a » a и выражение (1) запишем:
Знак минус означает, что сила 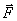
Основное уравнение динамики вращательного движения для физического маятника запишется:
Момент силы относительно оси О с учетом (2):
где l – расстояние от центра масс С до оси О.
Угловое ускорение маятника:
Поставив (4) и (5) в уравнение (3), получим:
По структуре уравнение (6) является дифференциальным уравнением гармонических колебаний с циклической частотой w . Период колебаний физического маятника равен:
Отсюда момент инерции физического маятника:
называется приведенной длиной физического маятника, равной длине математического маятника, имеющего тот же период колебаний, что и физический, т.е.
Точка О1, лежащая на прямой, проведенной через точку подвеса О и центр масс С, на расстоянии приведенной длины l 0 от оси вращения, называется центром качания маятника (рис.1). Центр качания лежит всегда ниже центра масс. Точка подвеса О и центр качания О1 сопряжены друг с другом, т.е. перенос точки подвеса в центр качания не меняет периода колебания маятника. Точка подвеса и центр качания обратимы, а расстояние между этими точками представляет собой приведенную длину l 0 одного из типов физического маятника, так называемого оборотного маятника.
Обозначим через J 0 момент инерции маятника относительно оси, проходящей через его центр масс. На основании теоремы Штейнера момент инерции J относительно любой оси, параллельной первой:
где m – масса маятника, l – расстояние между осями.
Тогда при подвешивании маятника за точку подвеса О период колебаний:
а при подвешивании за центр качания О 1 , когда маятник находится в перевернутом положении, период:
где l 2 и l 1 – расстояние между центром масс и соответствующими осями колебаний.
Из уравнений (9) и (10):
Формула (11) остается справедливой при колебаниях маятника относительно двух произвольных осей О и О / , не обязательно сопряженных, но расположенных по разные стороны от центра масс маятника.
Описание рабочей установки и метода измерений.
Для определения ускорения свободного падения применяется прибор ФП-1 (рис.2),
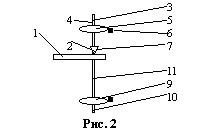
состоящий из настенного кронштейна 1, на котором смонтированы подушки 2 опорных призм и физического маятника представляющего собой однородный металлический стержень 11, на котором крепятся чечевицы 5 и 9. Чечевица 9 закреплена жестко и является неподвижной. Чечевица 5, находящаяся на конце стержня, может перемещаться по шкале 3 с нониусом 4 и фиксируется в нужном положении винтом 6. Маятник можно подвешивать на опорные призмы 7 и 10. В комплект прибора входит специальная подставка для определения положения центра масс маятника. Перемещением чечевицы 5 можно добиться равенства периодов колебаний маятника при подвесе его на опорные призмы 7 и 10, и тогда оси колебаний становятся сопряженными, расстояние между опорными призмами становится равным приведенной длине физического маятника.
Величина ускорения свободного падения определяется на основе формулы (11). Эксперимент сводится к измерению величин Т 1 , Т2, l 1 , l 2 . Формула (8) является исходной для определения момента инерции физического маятника.
1) Определение ускорения свободного падения .
1. Подвесить маятник на опорную призму 7, отклоняют на небольшой угол и измеряют секундомером время t 1 30-50 полных колебаний. Опыт повторяют не менее 5 раз и находят среднее значение времени t 1 > выбранного числа колебаний.
2. Определяют период колебания:
где n – число колебаний.
3. Для нахождения положения центра масс маятника снять его с подушек опорных призм и балансировать на горизонтальном ребре призмы, укрепленном на столе до тех пор, пока моменты сил тяжести, действующие на правую и левую часть маятника окажутся равными. В случае равновесия центр масс маятника будет расположен в стержне против точки опоры. Не снимая маятник с ребра призмы, линейкой измеряют расстояние l 1 между опорой 7 и центром масс.
4. Перевернув маятник, подвешивают его на опорную призму 10. Выбрать то же число колебаний n и, повторить опыт не менее 5 раз, находят период колебания:
При этом измеренные значения периодов Т 1 и Т2 должны отличаться не более чем на 5%
5. Найти расстояние l 2 между ребром опорной призмы 10 и центром масс: l 2 = l 0 – l 1 , где l 0 – расстояние между ребрами опорных призм 7 и 10 (для данного маятника l 0 =0,730м ).
6. Вычисляют среднее значение g > по формуле (11)
7. Оценивают абсолютную погрешность результата, исходя из табличного значения искомой величины g табл для широты г. Братска. Найти относительную погрешность.
8. Результаты измерений и вычислений заносят в таблицу 1.
Уравнение динамики вращательного движения физического маятника
«Физика — 10 класс»
Угловое ускорение.
Ранее мы получили формулу, связывающую линейную скорость υ, угловую скорость ω и радиус R окружности, по которой движется выбранный элемент (материальная точка) абсолютно твёрдого тела, которое, вращается относительно неподвижной оси:
Мы знаем, что линейные скорости и ускорения точек твёрдого тела различны. В то же время угловая скорость всех точек твёрдого тела одинакова.
Угловая скорость — векторная величина. Направление угловой скорости определяется по правилу буравчика. Если направление вращения ручки буравчика совпадает с направлением вращения тела, то поступательное движение буравчика указывает направление вектора угловой скорости (рис. 6.1).
Однако равномерное вращательное движение встречается довольно редко. Гораздо чаще мы имеем дело с движением, при котором угловая скорость изменяется, очевидно, это происходит в начале и конце движения.
Причиной изменения угловой скорости вращения является действие на тело сил. Изменение угловой скорости со временем определяет угловое ускорение.
Bектор угловой скорости — это скользящий вектор. Независимо от точки приложения его направление указывает направление вращения тела, а модуль определяет быстроту вращения,
Среднее угловое ускорение равно отношению изменения угловой скорости к промежутку времени, за которое это изменение произошло:
При равноускоренном движении угловое ускорение постоянно и при неподвижной оси вращения характеризует изменение угловой скорости по модулю. При увеличении угловой скорости вращения тела угловое ускорение направлено в ту же сторону, что и угловая скорость (рис. 6.2, а), а при уменьшении — в противоположную (рис. 6.2, б).
Так как угловая скорость связана с линейной скоростью соотношением υ = ωR, то изменение линейной скорости за некоторый промежуток времени Δt равно Δυ =ΔωR. Разделив левую и правую части уравнения на Δt, имеем 
Если время измерено в секундах, а угловая скорость — в радианах в секунду, то одна единица углового ускорения равна 1 рад/с 2 , т. е. угловое ускорение выражается в радианах на секунду в квадрате.
Неравномерно движутся при запуске и остановке любые вращающиеся тела, например ротор в электродвигателе, диск токарного станка, колесо автомобиля при разгоне и др.
Момент силы.
Для создания вращательного движения важно не только значение силы, но также и точка её приложения. Отворить дверь, оказывая давление около петель, очень трудно, в то же время вы легко её откроете, надавливая на дверь как можно дальше от оси вращения, например на ручку. Следовательно, для вращательного движения существенно не только значение силы, но и расстояние от оси вращения до точки приложения силы. Кроме этого, важно и направление приложенной силы. Можно тянуть колесо с очень большой силой, но так и не вызвать его вращения.
Момент силы — это физическая величина, равная произведению силы на плечо:
M = Fd,
где d — плечо силы, равное кратчайшему расстоянию от оси вращения до линии действия силы (рис. 6.3).
Очевидно, что момент силы максимален, если сила перпендикулярна радиус-вектору, проведённому от оси вращения до точки приложения этой силы.
Если на тело действует несколько сил, то суммарный момент равен алгебраической сумме моментов каждой из сил относительно данной оси вращения.
При этом моменты сил, вызывающих вращение тела против часовой стрелки, будем считать положительными (сила 


Основное уравнение динамики вращательного движения. Подобно тому как опытным путём было показано, что ускорение тела прямо пропорционально действующей на него силе, было установлено, что угловое ускорение прямо пропорционально моменту силы:
Пусть на материальною точку, движующуюся по окружности, действует сила 
Заметим, что в данном случае r — кратчайшее расстояние от оси вращения до материальной точки и соответственно точки приложения силы.
Произведение массы материальной точки на квадрат расстояния до оси вращения называют моментом инерции материальной точки и обозначают буквой I.
Таким образом, уравнение (6.1) можно записать в виде Iε = М, откуда
Уравнение (6.2) называют основным уравнением динамики вращательного движения.
Уравнение (6.2) справедливо и для вращательного движения твёрдого тела, имеющего неподвижную ось вращения, где I — момент инерции твёрдого тела, а М — суммарный момент сил, действующих на тело. В этой главе при расчёте суммарного момента сил мы рассматриваем только силы или их проекции, принадлежащие плоскости, перпендикулярной оси вращения.
Угловое ускорение, с которым вращается тело, прямо пропорционально сумме моментов сил, действующих на него, и обратно пропорционально моменту инерции тела относительно данной оси вращения.
Если система состоит из набора материальных точек (рис. 6.6), то момент инерции этой системы относительно данной оси вращения ОО’ равен сумме моментов инерции каждой материальной точки относительно этой оси вращения: I = m1r 2 1 + m2r 2 2 + . .
Момент инерции твёрдого тела можно вычислить, разделив тело на малые объёмы, которые можно считать материальными точками, и просуммировать их моменты инерции относительно оси вращения. Очевидно, что момент инерции зависит от положения оси вращения.
Из определения момента инерции следует, что момент инерции характеризует распределение массы относительно оси вращения.
Приведём значения моментов инерции для некоторых абсолютно твёрдых однородных тел массой m.
1. Момент инерции тонкого прямого стержня длиной l относительно оси, перпендикулярной к стержню и проходящей через его середину (рис. 6.7), равен:
2. Момент инерции прямого цилиндра (рис. 6.8), или диска относительно оси ОО’, совпадающей с геометрической осью цилиндра или диска:
3. Момент инерции шара радиусом R относительно оси, проходящей через его центр:
4. Момент инерции тонкого обруча радиусом R относительно оси, проходящей через его центр:
Момент инерции по физическому смыслу во вращательном движении играет роль массы, т. е. он характеризует инертность тела по отношению к вращательному движению. Чем больше момент инерции, тем сложнее тело заставить вращаться или, наоборот, остановить вращающееся тело.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Физического маятника
Определение момента инерции тел методом колебаний
Физический маятник – это твёрдое тело, способное совершать колебания вокруг оси, лежащей выше его центра масс. Такое «устройство» оказывается весьма полезным. Так, с его помощью очень просто и с огромной степенью точности определяется ускорение силы тяжести. Также физический маятник позволяет определять моменты инерции различных твёрдых тел.
Малые колебание маятника вокруг оси – это его небольшие повороты в противоположные стороны, поэтому понять колебания физического маятника – это понять механику вращения. Механика вращения имеет тесную аналогию с механикой поступательного движения. Аналогия проявляется в основных понятиях механики, её идеях и закономерностях, и как следствие – в формулах и уравнениях, что удобно представить в виде «таблицы аналогий », которую следует твердо усвоить:
Поступательное движение Вращательное движение
| t время | t время |
| s путь | φ угловой путь (угол поворота тела вокруг оси) |
| v = ds/dt ≈ ∆s/∆t скорость (путь, пройденный за единицу времени | ω = dφ/dt ≈ ∆φ /∆t угловая скорость (угол поворота тела за единицу времени |
| a= dv/dt= d 2 s/dt 2 ускорение (изменение скорости тела за единицу времени) | ε = dω/dt= d 2 φ//dt 2 угловое ускорение (изменение угловой скорости за единицу времени) |
| F – сила (мера воздействия одного тела на другое; причина, изменяющая состояние движения) | M – момент силы (способность силы поворачивать тело; причина, изменяющая состояние вращения) |
| m – масса (мера инертности тела) | Iz — момент инерции (инертность тела при вращении) |
| p= mv – импульс ( запас движения) | L = Izω — вращательный импульс; он же – момент импульса ( запас вращения) |
Основной закон динамики (уравнение движения)
 a=F/m a=F/m | ε =M/Iz |
(Рекомендуем студенту дополнить этот перечень аналогий для кинематики равномерного и равноускоренного движения, а также для работы, энергии и законов сохранения).
Мы видим, что в динамике вращения появились три новые величины с замысловатыми названиями: момент силы, момент инерции, момент импульса (он же угловой момент, он же вращательный импульс!). Да не болит голова у читателя по поводу таких названий; они появились в результате терминологических недоразумений прошлых веков с добавкой неадекватности перевода с иностранных языков; совершенно бесполезно вникать в смысл этих названий. Их надо просто запомнить. Для момента импульса это недоразумение достигает максимума – целых три названия. К счастью, одно из них оказалось порядочным – вращательный импульс, что просто отражает его аналогию соответствующей величине поступательного движения – обычному импульсу.
Дадим пояснения моменту силы M и моменту инерции Iz .
Момент силы. Возьмём твёрдое тело, закреплённое на оси. Приложим к нему в некоторой точке силу, и пусть линия действия силы пересекает ось вращения. Такая сила либо изогнёт ось вращения, либо вырвет ось из своего укрепления вместе с телом, ничего более.
Изменим немного опыт – сдвинем линию действия той же силы от оси на расстояние l . Эффект скажется незамедлительно: тело начнёт легко поворачиваться. Сила приобрела способность поворачивать тело. Эту способность силы поворачивать называют «моментом силы». Повседневный опыт говорит, что способность силы поворачивать тело зависит не только от силы, но и от «плеча силы» l (кратчайшего расстояния от линии действия силы до оси вращения). В итоге величина момента силы равна произведению силы на плечо:
Момент инерции относительно оси. Как уже было отмечено в «таблице аналогий», момент инерции (не обращать внимание на заумное название!) – величина, характеризующая инертность тела при вращении. Рассмотрим два совершенно одинаковых по форме и размерам волчка, но с заметно отличающими массами, скажем, алюминиевый и свинцовый. Мы легко обнаружим, что раскрутить до некоторой скорости (а так же потом остановить!) алюминиевый волчок гораздо легче, чем свинцовый. Значит, инертность тела при его вращении пропорциональна массе.
Далее, если бы у нас была возможность сильно расплющить любой волчок, отодвинув значительную часть его массы как можно дальше от оси вращения, превратив его в диск, то мы бы тот час обнаружили, что раскручивать (и останавливать) его стало заметно труднее, по сравнению с тем, когда он был компактным. Значит, инертность тела при вращении зависит не только от массы, но и от степени удаления её частей от оси вращения.
Момент инерции материальной точки массы m, находящейся на расстоянии r относительно оси z(рис.1), есть величина, равная произведению её массы на квадрат расстояния до оси вращения
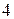
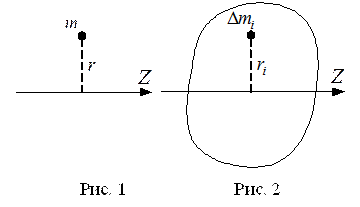
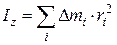

В пределе, когда Dmi строго превращаются в материальные точки, сумма(3)сводится к интегралу по объёму тела, и для тел простой (правильной) формы она точно вычисляется (таблицу моментов инерции тел правильной формы можно найти в справочниках и учебниках по общей физике). Отметим в заключение полезную формулу, известную как теорема Штейнера, позволяющую найти момент инерции тела относительно произвольной оси Z, если известен момент инерции тела Ic относительно оси, проходящей через центр инерции C (он же — центр масс, он же — центр тяжести) и параллельной данной оси:
здесь m – масса тела, a – расстояние между осями.
Теперь мы готовы к рассмотрению колебаний физического маятника (рис.3). Если отклонить его от положения равновесия на малый угол φ и предоставить самому себе, он начнёт совершать «малые» колебания. Для описания колебаний будем использовать один из основных способов решения физических задач – метод уравнения движения.
Уравнение движения в динамике вращения уже записано в «таблице аналогий»; оно отражает основной закон динамики вращения: если на тело действует внешняя сила, приводящая к возникновению момента силы, то тело вращается, причём его угловое ускорение пропорционально моменту силы и обратно пропорционально его моменту инерции:
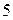
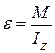
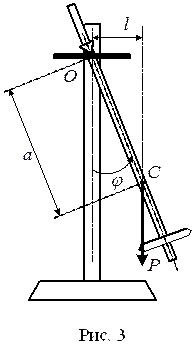
M = -Pl = — Pa sinφ = — mga sinφ ≈ — mgaφ (6)
Здесь учтено, что при малых отклонениях маятника синус угла можно заменить его аргументом (выраженным в радианах) sinφ ≈φ. Знак минус говорит о том, что при отклонении маятника на угол φ против часовой стрелки возникает момент силы тяжести, стремящийся повернуть маятник по часовой стрелке, т.е. возвратить его к положению равновесия.
В уравнении (5) искомая величина Iz. Остаётся расшифровать угловое ускорение. Угол отклонения φ (угловой путь!)зависит от времени, а угловое ускорение всегда есть вторая производная углового пути по времени (см. «таблицу аналогий»):
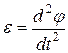
Подставляя (6) и (7) в (5), получаем уравнение движения малых колебаний физического маятника:
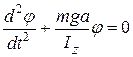
Из математики известно, что решение такого уравнения существенно зависит от знака коэффициента при φ . Величина mga/IZ заведомо положительна. Чтобы подчеркнуть это важное обстоятельство, mga/IZ записывают в виде квадрата некоторой действительной величины wo:
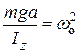
Теперь уравнение движения маятника принимает вид стандартного уравнения движения для гармонических колебаний
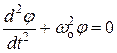
Решение этого уравнения представляет собой гармоническую функцию:
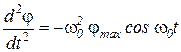
В гармоническом колебании (10) φmax – амплитуда колебаний, а woобретает точныйсмысл циклической частоты – числа колебаний за 2π секунд. (Учитывая, что за период колебания Т аргумент косинуса возрастает на 2π, имеем wo(t+T)=wot+2π, откуда wo =2π/T, т.е. именно число периодов за 2π секунд).
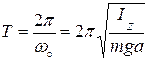
В итоге получаем формулу для экспериментального определения момента инерции физического маятника:
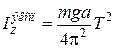
http://class-fizika.ru/10_a226.html
http://helpiks.org/7-37747.html