Техническая механика
Динамика системы материальных точек
Уравнение поступательного движения твердого тела
Механической системой материальных точек называется совокупность материальных точек, каким-то образом связанных межу собой.
Всякое твердое тело можно считать неизменяемой механической системой материальных точек. Силы взаимодействия точке данной системы называются внутренними силами; силы, с которыми действуют на данную систему другие точки, не входящие в эту систему, — внешними.
Пусть твердое тело массой m движется под действием силы F поступательно с ускорением а (рис. 1) .
Разобьем тело на ряд материальных точек с массами m1 и применим принцип Даламбера, не забывая при этом, что внутренние силы в уравнение равновесия не входят, так как на основании третьего закона Ньютона их сумма для системы в целом равна нулю.
В каждой материальной точке приложим силу инерции Fi ин = — mia и составим уравнение равновесия:
ΣX = 0 ; F – ΣFi ин = 0 ,
Так как при поступательном движении все точки тела имеют одинаковые ускорения, то а можно вынести за знак суммы, т. е.
Согласно второму закону Ньютона векторы силы F и ускорения а совпадают по направлению, поэтому можно записать:
Это и есть уравнение поступательного движения твердого тела. Очевидно, что это уравнение ничем не отличается от основного уравнения динамики точки, следовательно, все формулы динамики точки применимы для тела, движущегося поступательно.
Уравнение вращательного движения твердого тела
Пусть твердое тело под действием системы сил вращается вокруг неподвижной оси z с угловым ускорением α (рис. 2) .
Разобьем тело на ряд материальных точек с массами mi и применим, как и в предыдущем случае, принцип Даламбера (Д’Аламбера).
К каждой материальной точке приложены касательная и нормальная силы инерции. Составим уравнение равновесия:
Моменты реакций подшипника и подпятника, а также сил Fτi ин относительно оси z равны нулю, так как линии действия этих сил пересекают ось; сумма моментов внешних сил относительно оси вращения называется вращающим моментом .
Тогда
Выражение Σ(miri 2 ) называют моментом инерции тела относительно оси и обозначают J :
Момент инерции тела относительно оси есть сумма произведений масс материальных точек, составляющих это тело, на квадрат расстояния от них до этой оси.
В результате получим формулу:
которая называется уравнением вращательного движения твердого тела. В этой формуле J – момент инерции тела относительно оси вращения.
Единица момента инерции — [J] = [mr 2 ] = [m][r 2 ] = кг×м 2 .
Момент инерции играет во вращательном движении такую же роль, какую масса играет в поступательном движении, т. е. момент инерции есть мера инертности вращающегося тела.
В качестве примера определим момент инерции тонкого однородного сплошного диска, радиус которого R , толщина s , масса m , относительно оси, перпендикулярной плоскости диска и проходящей через его центр О (см. рис 3) .
Разобьем диск на элементарные кольца переменного радиуса r , шириной dr и толщиной s . Согласно определению момент инерции такого кольца равен
dJ = dΣ(mir 2 ) = r 2 dΣmi = r 2 dm = r 2 2πr drsρ = 2πsρ r 3 dr ,
где ρ – плотность материала диска.
Просуммировав моменты инерции всех элементарных колец, получим момент инерции всего диска:
J = ∫ 2πsρ r 3 dr = 2πsρ ∫ r 3 dr = 2πsρ r 4 /4 = πsρ r 4 /2 .
Так как масса диска m = πr 2 sρ , то можно записать: J = mR 2 /2 .
Нетрудно понять, что момент инерции однородного сплошного прямоугольного кругового цилиндра радиусом R и массой m любой высоты определяют по такой же формуле. Чтобы убедиться в этом, достаточно мысленно разбить цилиндр плоскостями, параллельными основанию на тонкие диски, и просуммировать моменты инерции всех дисков.
Моменты инерции тел вращения
На основе теоретических выкладок, изложенных выше, мы установили, что момент инерции круглого диска и цилиндрического тела можно определить по формуле
Аналогичные формулы можно вывести для определения моментов инерции других геометрических тел, наиболее часто встречающихся при расчетах и решении задач технической механики.
Моменты инерции для некоторых других однородных тел можно определить по формулам, которые приводятся здесь без вывода.
Шар массой m , радиусом R относительно диаметра:
Тонкий стержень массой m , длиной l относительно оси, проходящей перпендикулярно стержню через его конец:
Тонкая сферическая оболочка массой m , радиусом R относительно диаметра:
Пустотелый вал массой m , наружным радиусом R и радиусом отверстия r относительно оси:
Момент инерции Jz тела относительно какой-либо оси z , параллельной центральной (т. е. проходящей через центр тяжести С тела), равен сумме центрального момента инерции Jc и произведения массы m тела на квадрат расстояния а между этими осями:
Из этой формулы (ее вывод здесь не приводится) следует, что из всех моментов инерции тела относительно параллельных осей наименьшим будет момент инерции относительно центральной оси , т. е. центральный момент инерции.
Иногда момент инерции определяют по формуле: J = mrи 2 , где rи – радиус инерции тела :
Физический смысл радиуса инерции следующий: если массу тела сосредоточить в одной точке (такая масса называется приведенной) и поместить ее от оси вращения на расстоянии, равном радиусу инерции, то момент инерции приведенной массы будет равен моменту инерции данного тела относительно той же оси.
Удвоенный радиус инерции тела называется диаметром инерции : Dи = 2rи .
В практике иногда вместо момента инерции пользуются понятием махового момента GDи 2 .
Маховым моментом называется произведение силы тяжести G вращающегося тела на квадрат его диаметра инерции.
Единица махового момента — Н×м 2 .
Между маховым моментом и моментом инерции существует простая зависимость:
GDи 2 = 4g J = 39,24 J .
Кинетическая энергия твердого тела
Кинетическая энергия твердого тела равна сумме кинетических энергий материальных точек, составляющих данное тело:
Определим выражения для кинетической энергии твердого тела для трех случаев движения.
Тело движется поступательно
Учитывая, что при поступательном движении тела все его точки имеют одинаковую траекторию и одинаковые скорости, можно записать:
Следовательно, при поступательном движении твердого тела его кинетическая энергия вычисляется по той же формуле, что и кинетическая энергия материальной точки.
Тело вращается вокруг неподвижной оси
Кинетическая энергия твердого тела, вращающегося вокруг неподвижной оси, равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости.
Тело движется плоскопараллельно
Как известно из кинематики, сложное плоскопараллельное движение твердого тела в каждый данный момент времени можно считать простейшим вращательным движением вокруг мгновенной оси (метод мгновенных центров скоростей) .

где ОС – расстояние центра тяжести С тела от мгновенной оси вращения О .
Момент инерции Jо относительно мгновенной оси вращения определяют по формуле:
где Jс — момент инерции относительно центральной оси или центральный момент инерции.
Кинетическую энергию тела, движущегося плоскопараллельно, определяют следующим образом:
Кпп = Jоω 2 /2 = (Jс + mОС 2 ) ω 2 /2 = (Jсω 2 )/2 + mOC 2 /2×vс 2 /ОС 2 ,
Кинетическая энергия твердого тела, движущегося плоскопараллельно, равна сумме кинетических энергий в поступательном движении вместе с центром тяжести и вращательном движении вокруг центральной оси, перпендикулярной основной плоскости.
В заключение сформулируем теорему об изменении кинетической энергии системы тел:
Изменение кинетической энергии системы тел при некотором перемещении равно алгебраической сумме работ всех внешних (активных и реактивных) и внутренних сил, действовавших на систему при указанном перемещении:
Кинетическая энергия системы тел равна сумме кинетических энергий каждого тела в отдельности.
Если тело твердое, то сумма работ его внутренних сил равна нулю. При некоторых связях, называемых идеальными, работа реактивных сил тоже будет равна нулю.
Поступательное и вращательное движение
Движение твердого тела разделяют на виды:
- поступательное;
- вращательное по неподвижной оси;
- плоское;
- вращательное вокруг неподвижной точки;
- свободное.
Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.
Поступательное криволинейное движение. Угол поворота тела
Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.
Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.
Рисунок 1 . Поступательное криволинейное движение кабин колеса обзора
Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.
Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.
Если имеется поступательное движение, то общая скорость для всех точек тела υ → называется скоростью поступательного движения, а ускорение a → — ускорением поступательного движения. Изображение векторов υ → и a → принято указывать приложенными в любой точке тела.
Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.
Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.
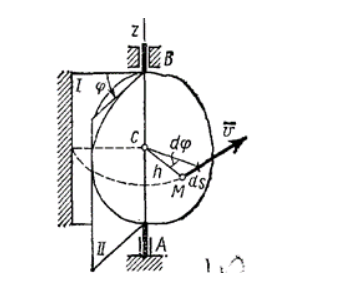
Чтобы определить положение вращающегося тела, необходимо начертить ось вращения, вдоль которой направляется ось A z , полуплоскость – неподвижную, проходящую через тело и движущуюся с ним, как показано на рисунке 2 .
Рисунок 2 . Угол поворота тела
Положение тела в любой момент времени будет характеризоваться соответствующим знаком перед углом φ между полуплоскостями, который получил название угол поворота тела. При его откладывании, начиная от неподвижной плоскости (направление против хода часовой стрелки), угол принимает положительное значение, против плоскости – отрицательное. Измерение угла производится в радианах. Для определения положения тела в любой момент времени следует учитывать зависимость угла φ от t , то есть φ = f ( t ) . Уравнение является законом вращательного движения твердого тела вокруг неподвижной оси.
При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.
Вращательное движение твердого тела характеризуется угловой скоростью ω и угловым ускорением ε .
Уравнения вращательного движения получают из уравнений поступательного, используя замены перемещения S на угловое перемещение φ , скорость υ на угловую скорость ω , а ускорение a на угловое ε .
Вращательное и поступательное движение. Формулы
| Поступательное | Вращательное |
| Равномерное | |
| s = υ · t | φ = ω · t |
| υ = c o n s t | ω = c o n s t |
| a = 0 | ε = 0 |
| Равнопеременное | |
| s = υ 0 t ± a t 2 2 | φ = ω 0 t ± ε · t 2 2 |
| υ = υ 0 ± a · t | ω = ω 0 ± ε · t |
| a = c o n s t | ε = c o n s t |
| Неравномерное | |
| s = f ( t ) | φ = f ( t ) |
| υ = d s d t | ω = d φ d t |
| a = d υ d t = d 2 s d t 2 | ε = d ω d t = d 2 φ d t 2 |
Задачи на вращательное движение
Дана материальная точка, которая движется прямолинейно соответственно уравнению s = t 4 + 2 t 2 + 5 . Вычислить мгновенную скорость и ускорение точки в конце второй секунды после начала движения, среднюю скорость и пройденный за этот промежуток времени путь.
Дано: s = t 4 + 2 t 2 + 5 , t = 2 с .
Найти: s ; υ ; » open=» υ ; α .
Решение
s = 2 4 + 2 · 2 2 + 5 = 29 м .
υ = d s d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 м / с .
» open=» υ = ∆ s ∆ t = 29 2 = 14 , 5 м / с .
a = d υ d t = 12 t 2 + 4 = 12 · 2 2 + 4 = 52 м / с 2 .
Ответ: s = 29 м ; υ = 37 м / с ; » open=» υ = 14 , 5 м / с ; α = 52 м / с 2
Задано тело, вращающееся вокруг неподвижной оси по уравнению φ = t 4 + 2 t 2 + 5 . Произвести вычисление мгновенной угловой скорости, углового ускорения тела в конце 2 секунды после начала движения, средней угловой скорости и угла поворота за данный промежуток времени.
Дано: φ = t 4 + 2 t 2 + 5 , t = 2 с .
Найти: φ ; ω ; » open=» ω ; ε .
Решение
φ = 2 4 + 2 · 2 2 + 5 = 29 р а д .
ω = d φ d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 р а д / с .
» open=» ω = ∆ φ ∆ t = 29 2 = 14 , 5 р а д / с .
ε = d ω d t = 12 2 + 4 = 12 · 2 2 + 4 = 52 р а д / с 2 .
Ответ: φ = 29 р а д ; ω = 37 р а д / с ; » open=» ω = 14 , 5 р а д / с ; ε = 52 р а д / с 2 .
Динамика поступательного и вращательного движений
Тема 2. Динамика поступательного и вращательного движений.
2) Основные характеристики динамики вращательного движения.
3) Работа и мощность. Механическая энергия.
Кинематика рассматривает движение тел, не интересуясь причинами, обуславливающими это движение и его изменение.
В основе динамики, которая изучает причины изменения движения, лежат законы Ньютона. Эти законы относятся к фундаментальным законам природы и доказать их справедливость или опровергнуть можно только опытом.
Второй закон Ньютона – основной закон динамики.
Этот закон выполняется только в инерциальных системах отсчета.
В динамике вводятся две новые физические величины – масса тела m и сила 

Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:
1. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам
2. Если силами разной величины подействовать на одно то же тело, то ускорения тела оказываются прямо пропорциональными приложенным силам.
Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики: Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:

Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила 

В международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с2. Эта единица называется ньютоном (Н).
Если на тело одновременно действуют несколько сил (например, и то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:
Если равнодействующая сила равна нулю, то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения.
Второй закон Ньютона также можно записать в виде:

Импульсом (количеством движения) называется векторная физическая величина, численно равная произведению массы тела на его скорость.

Основной единицей импульса тела в СИ является кг · м/с.
Тогда второй закон Ньютона окончательно примет вид :

Таким образом, скорость изменения импульса тела равна действующей на него силе.
1) Сила всемирного тяготения. Сила тяжести. Вес тела.
Закон всемирного тяготения был сформулирован Ньютоном – сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между центрами тел, т. е.

где 
Сила всемирного тяготения является центральной силой, т. е. направленной вдоль прямой соединяющей центры тел.
Под действием силы притяжения к Земле все тела падают с одинаковым ускорением, равным ускорению свободного падения 

Когда тело покоится относительно Земли, сила тяжести уравновешивается силой реакции опоры (или подвеса), удерживающей тело от падения. По третьему закону Ньютона, тело будет действовать на опору (или подвес) с силой 


Сила, с которой тело действует на опору или подвес, вследствие притяжения к Земле, называется весом тела.
Силы трения появляются при перемещении двух соприкасающихся тел или частей тела относительно друг друга.
Силы трения направлены по касательной к трущимся поверхностям, причем так, что они противодействуют относительному смещению этих поверхностей.
В случае сухого трения, сила трения возникает не только при скольжении одной поверхности по другой, но также и при попытках вызвать такое смещение. В этом случае сила трения называется силой трения покоя.
Опыт показывает, что максимальная сила трения покоя 

где N – сила нормального давления, 
Следует иметь в виду, что, помимо сил трения, при движении в жидкости или газе возникают силы сопротивления среды, которые могут быть гораздо больше сил трения. Характерной особенностью этих сил является их зависимость от скорости движения тела и его формы.
Если на вал с диском действуют две силы 


называется моментом силы 
Модуль вектора 

где 

называют моментом импульса материальной точки относительно точки.

называют моментом импульса твердого тела относительно точки.

называют моментом инерции материальной точки относительно оси вращения, а величину

моментом инерции твердого тела.
Любое твердое тело можно разбить на элементарные массы 


Момент инерции тела зависит от положения оси вращения. Для определения момента инерции тела относительно оси, не проходящей через центр масс, можно пользоваться теоремой Гюйгенса – Штейнера

где 



Момент инерции во вращательном движении играет ту же роль, что и масса в поступательном движении, т. е. является мерой инертности тела во вращательном движении.
Второй закон Ньютона для вращающегося тела можно записать в виде:

Так как 

Это выражение получило название основного уравнения динамики вращательного движения.
Энергия – универсальная количественная мера движения и взаимодействия всех видов материи.
С различными формами движения материи связывают различные формы энергии: механическую, внутреннюю, электромагнитную и т. д.
Чтобы количественно характеризовать процесс перехода энергии от одного тела к другому, в механике вводится физическая величина, называемая механической работой силы, приложенной к данному телу. Механическая работа — это мера превращения одного вида энергии в другой.
Если тело движется прямолинейно под действием постоянной силы 



В общем случае сила может изменяться как по величине, так и по направлению. Чтобы найти работу переменной силы, пройденный путь разбивается на большое число участков длиной 

а работа переменной силы на всем пути будет равна сумме элементарных работ:

При 

http://zaochnik.com/spravochnik/fizika/kinematika/postupatelnoe-i-vraschatelnoe-dvizhenie/
http://pandia.ru/text/78/157/30432.php