Затухающие колебания в контуре и их уравнение
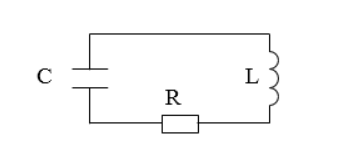
Существуют колебания в системе без источника энергии, называемые затухающими. Рассмотрим реальный контур с сопротивлением не равным нулю. Для примера используют контур с включенным сопротивлением R , с емкостью конденсатора C , с катушкой индуктивности L , изображенный на рисунке 1 . Колебания, происходящие в нем, — затухающие.
Именно наличие сопротивления становится главной причиной их затухания. Данный процесс возможен посредствам потерь энергии на выделение джоулева тепла. Аналог сопротивления в механике – действие сил трения.
Характеристики затухающих колебаний
Затухающие колебания характеризуют коэффициентом затухания β . Применив второй закон Ньютона, получим:
m a = — k x — y v , d 2 x d t 2 + r m d x d t + k m x = 0 , ω 0 2 = k m , β = r 2 m .
Из записи видно, что β действительно является характеристикой контура. Реже вместо β применяют декремент затухания δ ,
Значение a ( t ) является амплитудой заряда, силы тока и так далее, δ равняется количеству колебаний, а N e — период времени уменьшения амплитуды в e раз.
Для R L C контура применима формула с ω частотой.
При небольшой δ ≪ 1 говорят, что β ≪ ω 0 ω 0 = 1 L C — собственная частота, отсюда ω ≈ ω 0 .
При рассмотрении затухающих колебаний последовательного контура колебательный контур характеризуется добротностью Q :
Q = 1 R L C = ω 0 L R , где R , L и C — сопротивление, индуктивность, емкость, а ω 0 — частота резонанса. Выражение L C называют характеристическим или волновым сопротивлением. Для параллельного контура формула примет вид:
Q = R L C = R ω 0 L .
R является входным сопротивлением параллельного контура.
Эквивалентное определение добротности применяется при слабых затуханиях. Его выражают через отношение энергий:
Q = ω 0 W P d = 2 π f 0 W P d , называемое общей формулой.
Уравнения затухающих колебаний
Рассмотрим рисунок 1 . Изменение заряда q на конденсаторе в таком контуре описывается дифференциальным уравнением:
q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .
Если t = 0 , то заряд конденсатора становится равным q 0 , и ток в цепи отсутствует.
Если R > 2 L C изменения заряда не относят к колебаниям, разряд называют апериодическим.
Значение сопротивления, при котором колебания превращаются в апериодический разряд конденсатора, критическое R k .
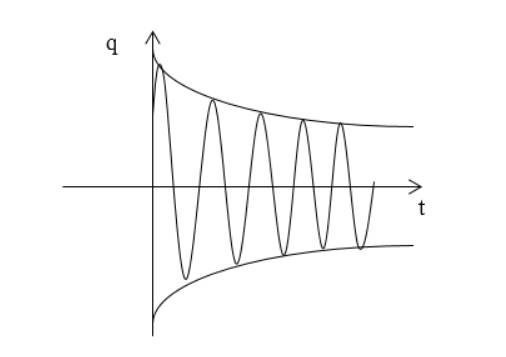
Функция изображается аналогично рисунку 2 .
Записать закон убывания энергии, запасенной в контуре W ( t ) при W ( t = 0 ) = W 0 с затухающими колебаниями. Обозначить коэффициент затухания в контуре β , а собственную частоту — ω 0 .
Решение
Отправная точка решения – это применение формулы изменения заряда на конденсаторе в R L C — контуре:
q ( t ) = q 0 e ( — β t ) cos ω t + a ‘ 0 = q 0 e — β t cos ( ω t ) .
Предположим, что при t = 0 , a ‘ 0 = 0 . Тогда применим выражение
Для нахождения I ( t ) :
I ( t ) = — ω 0 q 0 e ( — 2 β t ) sin ( ω t + α ) , где t g α = β ω .
Очевидно, что электрическая энергия W q запишется как:
W q = q 2 2 C = q 0 2 2 C e ( — 2 β t ) cos 2 ( ω t ) = W 0 e ( — 2 β t ) cos 2 ( ω t ) .
Тогда значение магнитной энергии контура W m равняется:
W m = L 2 ω 0 2 q 0 2 e ( — 2 β t ) sin 2 ω t + a = W 0 e — 2 β t sin 2 ω t + a .
Запись полной энергии будет иметь вид:
W = W q + W m = W 0 e ( — 2 β t ) ( cos 2 ( ω t ) + sin 2 ( ω t + a ) ) = = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + α ) .
Где sin α = β ω 0 .
Ответ: W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) .
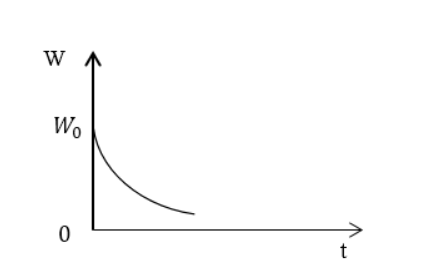
Применив результат предыдущего примера, записать выражение для энергии, запасенной в контуре W ( t ) , при медленно затухающих колебаниях. Начертить график убывания энергии.
Решение
Если колебания в контуре затухают медленно, то:
Очевидно, выражение энергии, запасенной в контуре, вычислим из
W ( t ) = W 0 e ( — 2 β t ) 1 + β ω 0 sin ( 2 ω t + a ) , предварительно преобразовав до W ( t ) = W 0 e ( — 2 β t ) .
Такое упрощение возможно по причине выполнения условия β ω 0 ≪ 1 , sin ( 2 ω t + a ) ≤ 1 , что означает β ω 0 sin ( 2 ω t + a ) ≪ 1 .
Ответ: W ( t ) = W 0 e ( — 2 β t ) . Энергия в контуре убывает по экспоненте.
Энергия затухающих колебаний
Характеристики затухающих колебаний.
1. Коэффициент затухания β.
Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону:
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 
, а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем 
. Из этих соотношений следует βτ = 1, отсюда 
.
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
2. Логарифмический декремент затухания δ— физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
,
где Азат.(t) и Азат.(t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).
3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
.
Так как энергия пропорциональна квадрату амплитуды, то
.
При малых значениях логарифмического декремента δ добротность колебательной системы равна
,
где Ne – число колебаний, за которое амплитуда уменьшается в “е” раз.
Энергия затухающих колебаний
Эта энергия складывается из потенциальной и кинетической 
П 
осле подстановки сюда выражений 
, 
из (1.3.1) получим зависимость 
, которая графически представлена на рисунке 1.3.2.Уменьшение энергии колебаний обусловлено работой силы сопротивления.
Энергия системыпропорциональна квадрату амплитуды и при затухающих колебаниях убывает по закону
где 
—энергия колебаний в начальный момент времени(рис.1.3.2).
В широком смысле, под волной понимают процесс распространения в пространстве колебаний или возмущений состояния вещества или поля с течением времени. Математически этот процесс выражается функцией, описывающей распространение в пространстве изменений какой-либо физической величины. Выделяют три типа волн: волны на поверхности жидкости, упругие (иначе механические) и электромагнитные.
Хар-ки бегущей волны:
Минимальное расстояние , на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны .
Длиной волны 
называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна 
) .
Если точки разделены расстоянием 
, их колебания происходят в противофазе.
2. Фазовая скорость волны.
Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой .
Фазовая скорость 
— это скорость распространения данной фазы колебаний, т.е. скорость волны.
Связь длины волны , фазовой скорости и периода колебаний Т задается соотношением:
.
3. Фазовая скорость различна для разных сред. В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:
,
где 
— модуль сдвига среды, 
-ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
Фазовая скорость упругих продольных волн в твердом теле равна
,
где Е — модуль Юнга, — плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
Фазовая скорость продольных волн в жидкости и газе определяется соотношением:
,
где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема, — плотность невозмущенной среды.
Фазовая скорость продольных волн в идеальном газе задается формулой:
,
— показатель адиабаты, 
— молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа ( 
) и от его термодинамического состояния (Т).
4. Фронт волны. Волновая поверхность.
При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.
Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом .
Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью .
Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.
5. Уравнение бегущей волны.
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
,
где 
— смещение точки О от положения равновесия, 
— частота, А – амплитуда колебаний.
6. Волновое уравнение.
,
где 
— фазовая скорость волны.
Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что 
есть функция двух переменных t и y.
7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды.
Если смещение любой точки среды с координатой y в момент времени t задано уравнением:
,
то скорость этой точки есть величина 
, а ускорение — 
(5)
Уравнение (5) представляет собой уравнение плоской бегущей волны, распространяющейся вдоль положительного направления оси х. Из него можно определить отклонение частиц среды от равновесия в любой точке пространства с координатой х и в любой момент времени t при распространении указанной волны. Уравнение (5) соответствует случаю, когда частицам в начальный момент была сообщена начальная скорость. Если же в начальный момент частицам сообщено отклонение от положения равновесия без сообщения скорости, в (5) вместо синуса нужно поставить косинус. Аргумент косинуса или синуса называют фазой колебания. Фаза определяет состояние колебательного процесса в данный момент времени (знак и абсолютную величину относительного отклонения частиц от их положения равновесия). Из (5) видно, что фаза колебаний частиц, расположенных в плоскости х, меньше соответствующей величины для частиц, расположенных в плоскости х=0, на величину, равную 
.
Если плоская волна распространяется в направлении убывания х(налево), то уравнение (5) преобразуется к виду:
(6)
Если среда, в которой распространяется одновременно несколько волн, линейна, т. е. ее свойства не изменяются под действием возмущений, создаваемых волной, то к ним применимпринцип суперпозиции (наложения) волн:при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
С 
тоячие волны образуются в результате интерференции двух встречных плоских волн одинаковой частоты ω и амплитуды А.
Представим себе, что в точке S(рис.7.4) находится вибратор, от которого вдоль лучаOраспространяется плоская волна. Достигнув преграды в точке О, волна отразится и пойдёт в обратном направлении, т.е. вдоль луча распространяются две бегущие плоские волны: прямая и обратная. Эти две волны когерентны, так как рождены одним и тем же источником и, накладываясь друг на друга, будут интерферировать между собой.
Возникающее в результате интерференции колебательное состояние среды и называется стоячей волной.
В отличие от бегущей волны в стоячей волне не происходит переноса энергии. Энергия просто переходит из потенциальной (при максимальном смещении точек среды от положения равновесия) в кинетическую (при прохождении точками положения равновесия)в пределах между узлами, остающимися неподвижными.
Все точки стоячей волны в пределах между узлами колеблются в одинаковой фазе, а по разные стороны от узла – в противофазе.
Стоячие волны возникают, например, в закреплённой с обоих концов натянутой струне при возбуждении в ней поперечных колебаний. Причём в местах закреплений располагаются узлы стоячей волны.
Если стоячая волна устанавливается в воздушном столбе, открытом с одного конца (звуковая волна), то на открытом конце образуется пучность, а на противоположном – узел.
Концепция Эйнштейна позволяет отказаться от существования эфира и построить теорию, называемую ныне специальной теорией относительности (СТО) и и подтверждаемая всеми известными сегодня опытами.
В основе СТО лежат два постулата.
«Принцип постоянства скорости света».
Скорость света не зависит от скорости движения источника света, одинакова во всех инерциальных системах координат, и равна в вакууме с=3×10 8 м/с.
Позднее, в общей теории относительности (ОТО), опубликованной в 1916 году, утверждалось, что скорость света остается неизменной и в неинерциальных системах координат.
Затухающие колебания
Определение затухающих колебаний
Механическое движение всегда сопровождается трением. Трение приводит к рассеянию (диссипации) механической энергии. Диссипация энергии имеется в любых не идеализированных колебательных системах, она вызывает затухание собственных колебаний.
Затухающими колебаниями называют колебания, амплитуда которых постепенно уменьшается со временем из-за потерь энергии колебательной системой.
Уравнение колебаний пружинного маятника с затуханием
Иногда, если тело движется в веществе, силу сопротивления ($<\overline
\[<\overline
где $\beta $ — коэффициент сопротивления.
Данную силу учитывают в уравнении второго закона Ньютона при описании движения. Так, уравнение, которое описывает линейные колебания по вертикали (колебания по оси X) пружинного маятника, учитывающее силу трения принимает вид:
где $\dot
(где $<\omega >_0$- циклическая частота свободных незатухающих колебаний (собственная частота колебаний при $\gamma $=0) той же колебательной системы; $\gamma $ — коэффициент затухания) уравнение колебаний пружинного маятника с затуханием (2) преобразуем к виду:
Малые собственные колебания, затухающие вследствие сопротивления среды в любой физической системе (математический маятник, физический маятник, электрические колебания . ) описывают при помощи уравнения формы (4).
Уравнение затухающих колебаний имеет точное решение:
где $\omega =\sqrt<<\omega >^2_0-<\gamma >^2>$; $A_0$ — начальная амплитуда колебаний, задаваемая начальными условиями; $\varphi $ — постоянная из начальных условий. При $\gamma \ll <\omega >_0$, $\omega \approx <\omega >_0$, параметр $A_0e^<-\gamma t>$ можно считать медленно изменяющейся во времени амплитудой колебаний.
Затухание колебаний по экспоненте связано с тем, что силу сопротивления мы приняли пропорциональной скорости. Если использовать другую зависимость силы трения от скорости, то закон затухания изменится.
Диссипация энергии при затухающих колебаниях
Пусть затухание мало, при этом потеря энергии колебательной системой за один период много меньше, чем энергия колебаний.
Рассеяние энергии за период колебаний происходит не равномерно, ввиду осцилляции кинетической энергии ($E_k$). Уравнение убывания энергии при затухающих колебаниях будет иметь вид:
\[\frac
где $\frac
Так как мы считаем затухание малым, то $\left\langle E_k\right\rangle $ можно принять равным (как при свободных колебаниях) половине полной энергии осциллятора:
\[\left\langle E_k\right\rangle =\frac
В таком случае уравнение (6) можно записать в виде:
Выражение (8) отображает «сглаженное» поведение энергии колебаний (в случае, если детали изменения энергии за один период колебаний не интересны). Оно показывает, что скорость изменения энергии пропорциональна самой энергии. Решением уравнения (8) является функция:
где $E_0$ — величина энергии колебательной системы в начальный момент времени.
Так как энергия колебаний пропорциональна квадрату амплитуды ($E\sim A^2$), изменение амплитуды колебаний за большие отрезки времени (в сравнении с периодом колебаний) запишем в виде функции:
$A_0$ — начальная амплитуда колебаний.
Время жизни колебаний. Период затухающих колебаний. Декремент затухания
Из формулы (10) видно, что амплитуда затухающих колебаний убывает по экспоненте. За время $\tau =\frac<1><\gamma >$ амплитуда убывает в $e$ раз и это не зависит от $A_0$. Время $\tau $ в этом случае называют временем жизни колебаний (или временем релаксации) (не смотря на то, что в соответствии с выражением (9) колебания должны длиться бесконечно). Тезис о малости затухания означает, что время жизни колебаний не бесконечно, а много больше, чем их период ($\tau \gg T$). За время жизни происходит много колебательных движений.
Строго говоря, затухающие колебания не являются строго периодическими движениями. Периодом в данном случае считают промежуток времени между двумя последовательными максимальными отклонениями от положения равновесия.
Период затухающих колебаний считают равным:
Пусть $A\left(t\right)\ и\ A(t+T)$ — амплитуды двух последовательных колебаний, моменты времени которых отличаются на период. Отношение этих амплитуд, следуя (10) равно:
называют декрементом затухания. Натуральный логарифм декремента затухания ($\theta $):
называют логарифмическим декрементом затухания. Для колебательной системы $\theta $ постоянная величина.
Примеры задач с решением
Задание. Каков коэффициент затухания маятника ($\gamma $), если за $\Delta t$ амплитуда его колебаний уменьшилась в $n$ раз?
Решение. За основу решения задачи примем уравнение затухающих колебаний в виде:
По условию задачи имеем:
С другой стороны:
где $t_2-t_1=\Delta t$. Найдем натуральный логарифм от правой и левой части выражения (1.2), получим:
Выразим $\gamma $ из (1.3) учтем, что $\frac
Ответ. $\gamma =\frac<<\ln n\ >><\Delta t>$
Задание. Что представляет собой фазовая траектория затухающего колебания?
Решение. Фазовой траекторией называют траекторию движения в плоскости $\left(x;;v\right).$ По оси абсцисс откладывается отклонение $x$, по оси ординат откладывают скорость $v$. Каждому движению в момент времени $t$ соответствует изображающая точка, на указанной плоскости координаты ее $\left(x,v\right),$ они однозначно определены мгновенными значениями отклонения и скорости. Точка со временем движется и описывает траекторию (рис.1). В данном случае время выступает как параметр, уравнение фазовой траектории задет функция:
Фазовая траектория затухающего колебания, если
\[<\overline
представляет собой незамкнутую спираль, которая закручивается вокруг начала координат (рис.1). Если затухание колебаний малое, то есть за время жизни колебательная система совершает множество колебаний, количество витков спирали в фазовой плоскости будет таким же.
http://poisk-ru.ru/s38844t9.html
http://www.webmath.ru/poleznoe/fizika_46_zatuhajushhie_kolebanija.php