Уравнение для момента импульса материальной точки

Уравнение моментов: моменты силы, импульса и инерции

Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то характеристики движения механических систем по круговым траекториям вычисляют с помощью специального выражения, которое называется уравнением моментов. О каких моментах идет речь и в чем заключается смысл этого уравнения? Эти и другие вопросы раскрываются в статье.

Момент силы

Всем хорошо известна ньютоновская сила, которая, действуя на тело, приводит к сообщению ему ускорения. Когда же такая сила прилагается к объекту, который закреплен на некоторой оси вращения, то эту характеристику принято называть моментом силы. Уравнение момента силы может быть записано в следующем виде:

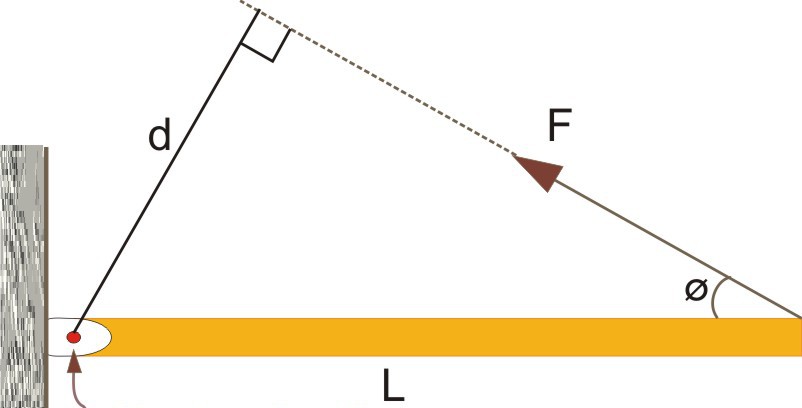
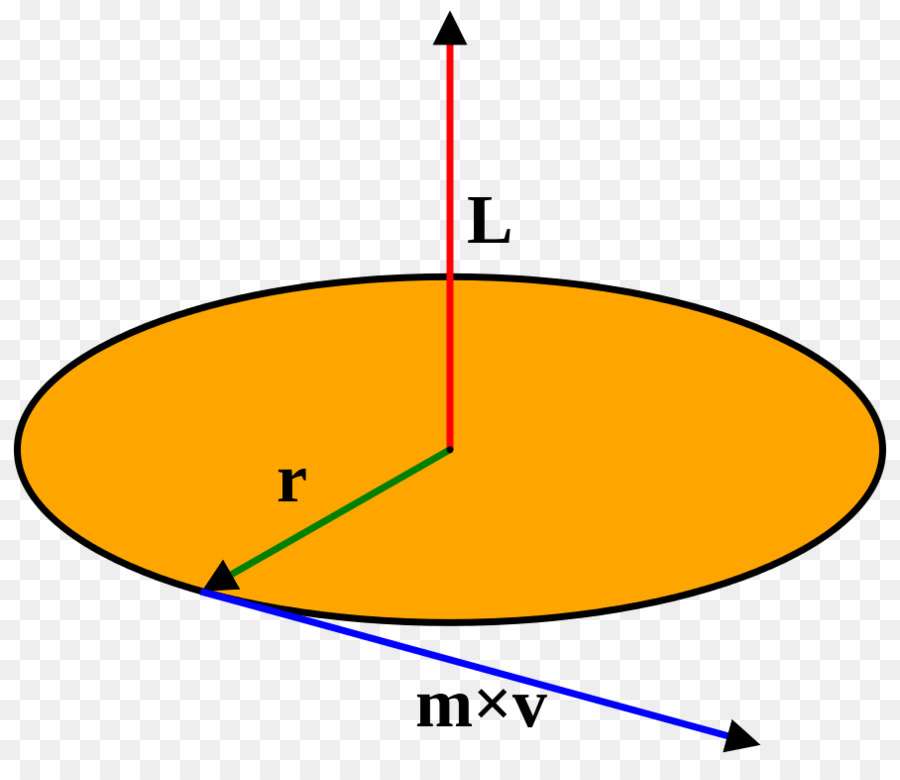
Рисунок, поясняющий это выражение, приведен ниже.

Здесь видно, что сила F¯ направлена к вектору L¯ под углом Φ. Сам же вектор L¯ полагается направленным от оси вращения (указана стрелкой) к точке приложения F¯.

Приведенная выше формула представляет собой произведение двух векторов, поэтому величина M¯ также является направленной. Куда будет повернут момент силы M¯? Это можно определить по правилу правой руки (четыре пальца направлены вдоль траектории от конца вектора L¯ к концу F¯, а отставленный палец большой показывает направление M¯).

На рисунке выше выражение для момента силы в скалярном виде примет форму:

Если внимательно всмотреться в рисунок, то можно увидеть, что L*sin(Φ) = d, тогда имеем формулу:

Величина d является важной характеристикой при вычислении момента силы, поскольку она отражает эффективность приложенной F к системе. Эту величину принято называть рычагом силы.

Физический смысл M заключается в способности силы совершить вращение системы. Эту способность может ощутить на себе каждый, если будет открывать дверь за ручку, толкая ее около петель, или же попробует открутить гайку коротким и длинным ключом.

Равновесие системы

Понятие о моменте силы оказывается очень полезным, когда рассматривают равновесие системы, на которую действуют несколько сил, и которая имеет ось или точку вращения. В таких случаях применяют формулу:

То есть система будет находиться в равновесии, если сумма всех моментов сил, приложенных к ней, нулевая. Заметим, что в этой формуле присутствует знак вектора над моментом, то есть при решении следует не забывать учитывать знак этой величины. Общепринятым правилом считается, что действующая сила, которая вращает систему против часовой стрелки, создает положительный M_i¯.

Ярким примером задач рассматриваемого типа являются проблемы с равновесием рычагов Архимеда.

Момент импульса

Это еще одна важная характеристика движения по окружности. В физике ее описывают произведением количества движения на рычаг. Уравнение момента импульса имеет такой вид:

Здесь p¯ — вектор импульса, r¯ — вектор, соединяющий вращающуюся материальную точку с осью.

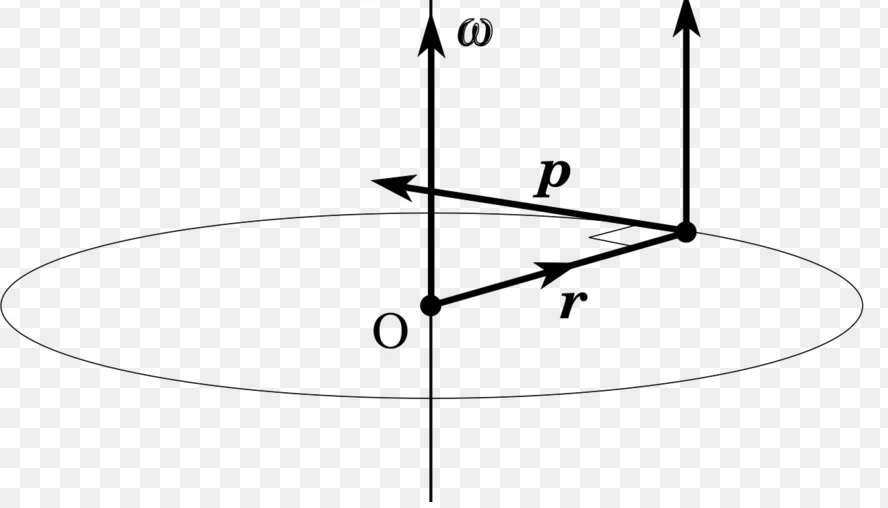
Поясняющий это выражение рисунок приведен ниже.

Здесь ω — угловая скорость, которая дальше появится в уравнении моментов. Заметим, что направление вектора T¯ находится по тому же правилу, что и M¯. На рисунке выше T¯ по направлению будет совпадать с вектором угловой скорости ω¯.

Физический смысл величины T¯ является таким же, как и характеристики p¯ в случае линейного движения, то есть момент импульса описывает количество вращательного движения (запасенную кинетическую энергию).

Момент инерции

Третья важная характеристика, без которой невозможно составить уравнение движения вращающегося объекта, — это момент инерции. Появляется он в физике в результате математических преобразований формулы для момента импульса материальной точки. Покажем, как это делается.

Представим величину T¯ в следующем виде:

T¯ = r¯*m*v¯, где p¯ = m*v¯

Пользуясь связью между угловой и линейной скоростями, можно переписать это выражение следующим образом:

T¯ = r¯*m*r¯*ω¯, где v¯ = r¯*ω¯

Последнее выражение запишем в виде:

Величина r 2 *m — это момент инерции I для точки массой m, которая совершает круговое движение вокруг оси на расстоянии от нее r. Этот частный случай позволяет ввести общее уравнение момента инерции для тела произвольной формы:

I — это аддитивная величина, смысл которой заключается в инерционности вращающейся системы. Чем больше I, тем труднее раскрутить тело, и необходимо приложить значительные усилия, чтобы его остановить.

Уравнение моментов

Мы рассмотрели три величины, название которых начинается со слова «момент». Это сделано было намеренно, поскольку все они связаны в одно выражение, получившее название уравнения 3 моментов. Выведем его.

Рассмотрим выражение для момента импульса T¯:

Найдем, как изменяется величина T¯ во времени, имеем:

Учитывая, что производная угловой скорости равна таковой для скорости линейной, деленной на r, а также раскрывая величину I, приходим к выражению:

dT¯/dt = m*r 2 *1/r*dv¯/dt = r*m*a¯, где a¯ = dv¯/dt — линейное ускорение.

Заметим, что произведение массы на ускорение — это не что иное, как действующая внешняя сила F¯. В итоге получаем:

Мы пришли к интересному выводу: изменение момента импульса равно моменту действующей внешней силы. Это выражение принято записывать в несколько иной форме:

M¯ = I*α¯, где α¯ = dω¯/dt — угловое ускорение.

Это равенство называется уравнением моментов. Оно позволяет рассчитать любую характеристику вращающегося тела, зная параметры системы и величину внешнего воздействия на нее.

Закон сохранения T¯

Полученный в предыдущем пункте вывод свидетельствует о том, что если внешний момент сил будет равен нулю, то момент импульса меняться не будет. В таком случае запишем выражение:

Эта формула носит название закона сохранения величины T¯. То есть любые изменения внутри системы суммарный момент импульса не меняют.

Этот факт используется фигуристами и балеринами во время их выступлений. Также его применяют, если необходимо выполнить поворот вокруг своей оси искусственного спутника, движущегося в космосе.

Закон сохранения момента импульса: формула, применение и особенности

При решении задач на движение тел в пространстве часто используют формулы сохранения кинетической энергии и импульса. Оказывается, что аналогичные выражения существуют и для вращающихся тел. В данной статье подробно рассматривается закон сохранения момента импульса (формулы соответствующие также приводятся) и дается пример решения задачи.

Процесс вращения и момент импульса

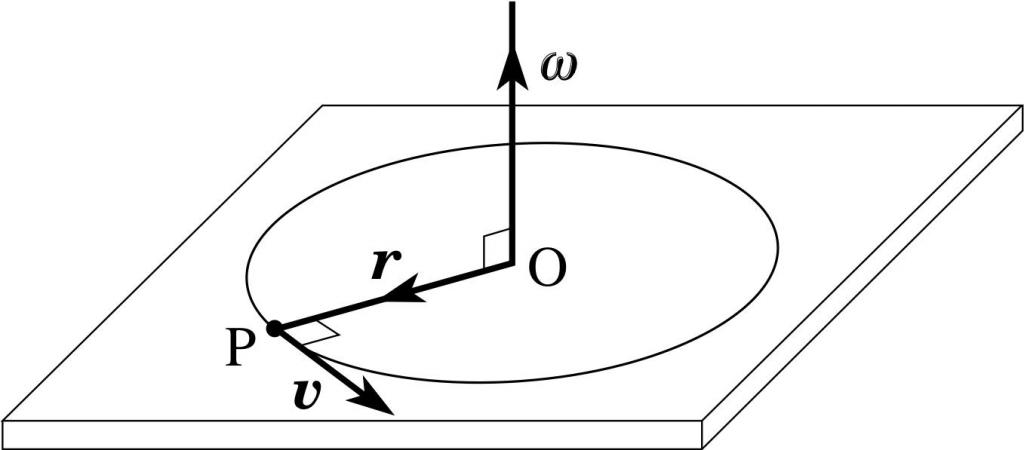
Перед тем как перейти к рассмотрению формулы закона сохранения момента импульса, необходимо познакомиться с этим физическим понятием. Проще всего его можно ввести, если воспользоваться рисунком ниже.

Вам будет интересно: Нарративный анализ: понятие и применение

На рисунке видно, что на конце вектора r¯, направленного от оси вращения и перпендикулярного ей, имеется некоторая материальная точка массой m. Эта точка движется по окружности названного радиуса с линейной скоростью v¯. Из физики известно, что произведение массы на линейную скорость называется импульсом (p¯). Теперь стоит ввести новую величину:

Вам будет интересно: Сульфат стронция: нахождение в природе, растворимость, применение

Здесь векторная величина L¯ представляет собой момент импульса. Чтобы перейти к скалярной форме записи, необходимо знать модули соответствующих значений r¯ и p¯, а также угол θ между ними. Скалярная формула для L имеет вид:

L = r*m*v*sin(θ) = r*p*sin(θ).

На рисунке выше угол θ является прямым, поэтому можно просто записать:

Из записанных выражений следует, что единицей измерения для L будут кг*м2/с.

Направление вектора момента импульса

Поскольку рассматриваемая величина является вектором (результат векторного произведения), то она будет иметь определенное направление. Из свойств произведения двух векторов следует, что их результат даст третий вектор, перпендикулярный плоскости, образованной первыми двумя. При этом направлен он будет таким образом, что если смотреть с его конца, то тело будет вращаться против часовой стрелки.

Результат применения этого правила показан на рисунке в предыдущем пункте. Из него видно, что L¯ направлен вверх, поскольку, если смотреть на тело сверху, его движение будет происходить против хода стрелки часов. При решении задач важно учитывать направление во время перехода к скалярной форме записи. Так, рассмотренный момент импульса считается положительным. Если бы тело вращалось по часовой стрелке, тогда в скалярной формуле перед L следовало бы поставить знак минуса (-L).

Аналогия с линейным импульсом

Вам будет интересно: Самые старые горы в мире: где находятся, фото, названия

Рассматривая тему момента импульса и закона его сохранения, можно проделать один математический трюк — преобразовать выражение для L¯, помножив и поделив его на r2. Тогда получится:

L¯ = r*m*v¯*r2/r2 = m*r2*v¯/r.

В этом выражении отношение скорости к радиусу вращения называется угловой скоростью. Она обычно обозначается буквой греческого алфавита ω. Эта величина показывает, на сколько градусов (радиан) сделает поворот тело по орбите своего вращения за единицу времени. В свою очередь, произведение массы на квадрат радиуса — это тоже физическая величина, имеющая собственное название. Обозначают ее I и называют моментом инерции.

В итоге формула для момента импульса преобразуется в следующую форму записи:

L¯ = I *ω¯, где ω¯= v¯/r и I=m*r2.

Выражение демонстрирует, что направление момента импульса L¯ и угловой скорости ω¯ совпадают для системы, состоящей из вращающейся материальной точки. Особый интерес представляет величина I. Ниже она рассмотрена подробнее.

Момент инерции тела

Введенная величина I характеризует «сопротивляемость» тела любому изменению скорости его вращения. То есть она играет точно такую же роль, что и инерция тела при линейном перемещении объекта. По сути I для кругового движения с физической точки зрения означает то же самое, что и масса при линейном движении.

Как было показано, для материальной точки с массой m, вращающейся вокруг оси на расстоянии от нее r, момент инерции рассчитать просто (I = m*r2), однако для любых других тел этот расчет будет несколько сложным, поскольку предполагает использование интеграла.

Для тела произвольной формы I можно определить при помощи следующего выражения:

I = ∫m(r2*dm) = ∫V(r2*ρ*dV), где ρ — плотность материала.

Вам будет интересно: Архаический период Древней Греции (IX–VIII вв. до н.э.)

Выражения выше означают, что для вычисления момента инерции следует разбить все тело на бесконечно малые объемы dV, умножить их на квадрат расстояния до оси вращения и на плотность и просуммировать.

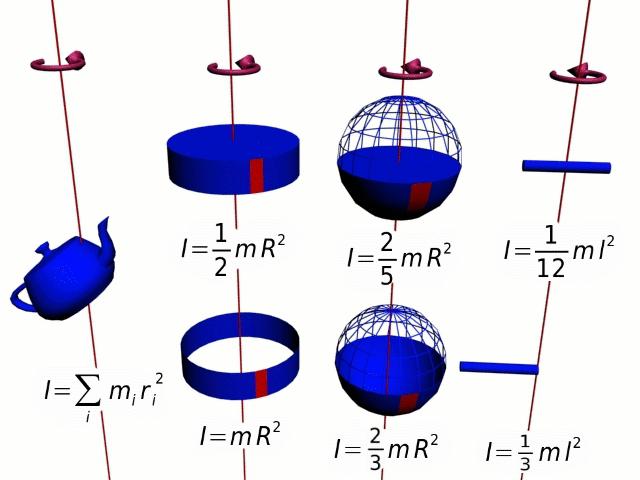
Для тел разной формы эта задача решена. Ниже приводятся данные для некоторых из них.

Материальная точка: I = m*r2.

Диск или цилиндр: I = 1/2*m*r2.

Стержень длиной l, закрепленный по центру: I = 1/12*m*l2.

Момент инерции зависит от распределенной массы тела относительно оси вращения: чем дальше от оси будет находиться большая часть массы, тем больше будет I для системы.

Изменение момента импульса во времени

Рассматривая момент импульса и закон сохранения момента импульса в физике, можно решить простую проблему: определить, как и за счет чего он будет изменяться во времени. Для этого следует взять производную по dt:

dL¯/dt = d(r¯*m*v¯)/dt = m*v¯*dr¯/dt+r*m*dv¯/dt.

Первое слагаемое здесь равно нулю, поскольку dr¯/dt = v¯ и произведение векторов v¯*v¯ = 0 (sin(0) = 0). Второе же слагаемое может быть переписано следующим образом:

dL¯/dt =r*m*a¯, где ускорение a = dv¯/dt, откуда:

Величина M¯, согласно определению, называется моментом силы. Она характеризует действие силы F¯ на материальную точку массой m, расположенную на расстоянии r от оси вращения.

Что показывает полученное выражение? Оно демонстрирует, что изменение момента импульса L¯ возможно только за счет действия момента силы M¯. Эта формула — закон сохранения момента импульса точки: если M¯=0, то dL¯/dt = 0 и L¯ является постоянной величиной.

Какие моменты сил могут изменить L¯ системы?

Существует два вида моментов сил M¯: внешние и внутренние. Первые связаны с силовым воздействием на элементы системы со стороны любых внешних сил, вторые же возникают за счет взаимодействия частей системы.

Согласно третьему закону Ньютона, любой силе действия соответствует направленная противоположно сила противодействия. Это означает, что суммарный момент силы любых взаимодействий внутри системы всегда равен нулю, то есть он не может повлиять на изменения момента импульса.

Величина L¯ может измениться только за счет внешних моментов сил.

Формула закона сохранения момента импульса

Формула для записи выражения сохранения величины L¯ в случае, если сумма внешних моментов сил равна нулю, имеет следующий вид:

Любые изменения момента инерции системы пропорционально отражаются на изменении угловой скорости таким образом, что произведение I*ω не меняет своего значения.

Вид этого выражения аналогичен закону сохранения линейного импульса (роль массы играет I, а роль скорости — ω). Если развивать аналогию дальше, то, помимо этого выражения, можно записать еще одно, которое будет отражать сохранение кинетической энергии вращения:

E = I *(ω)2/2 = const.

Применение закона сохранения момента импульса находит себя в целом ряде процессов и явлений, которые кратко охарактеризованы ниже.

Примеры использования закона сохранения величины L¯

Следующие примеры закона сохранения момента импульса имеют важное значение для соответствующих сфер деятельности.

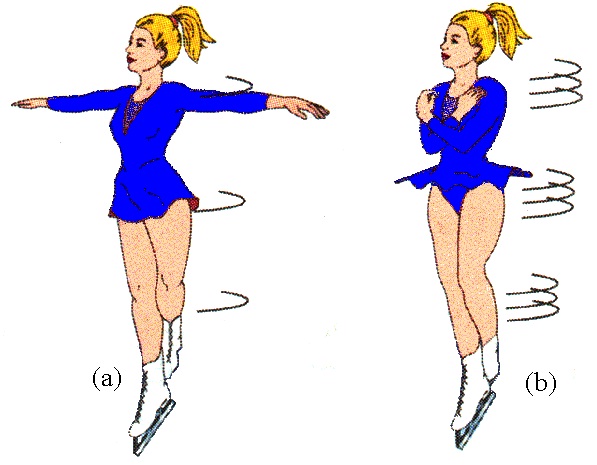
• Любой вид спорта, где необходимо совершать прыжки с вращением. Например, балерина или спортсмен по фигурному катанию начинает исполнение пируэта с вращением, разведя широко руки и отодвинув ногу от центра тяжести своего тела. Затем он прижимает ногу ближе к опорной и руки ближе к телу, уменьшая тем самым момент инерции (большая часть точек тела расположена близко к оси вращения). По закону сохранения величины L, должна увеличиться его угловая скорость вращения ω.

• Для изменения направления ориентации относительно Земли какого-либо искусственного спутника. Выполняется это так: спутник имеет специальный тяжелый «маховик», его приводит в движение электромотор. Общий момент импульса должен сохраняться, поэтому сам спутник начинает вращаться в противоположную сторону. Когда он примет нужную ориентацию в пространстве, маховик останавливают, и спутник также перестает вращаться.
• Эволюция звезд. По мере того как звезда сжигает свое водородное топливо, силы гравитации начинают преобладать над давлением ее плазмы. Этот факт приводит к уменьшению радиуса звезды до небольших размеров и, как следствие, к сильному увеличению скорости вращения угловой. Например, установлено, что нейтронные звезды, имеющие диаметр несколько километров, вращаются с гигантскими скоростями, делая один оборот за доли миллисекунды.

Решение задачи на закон сохранения L¯

Учеными установлено, что через несколько миллиардов лет Солнце, исчерпав энергетические запасы, превратится в «белого карлика». Необходимо рассчитать, с какой скоростью оно будет вращаться вокруг оси.

Для начала необходимо выписать значения необходимых величин, которые можно взять из литературы. Итак, сейчас данная звезда имеет радиус 696 000 км и один оборот вокруг своей оси делает за 25,4 земных суток (значение для области экватора). Когда она подойдет к концу своего эволюционного пути, то сожмется до размеров 7000 км (порядка радиуса Земли).

Полагая, что Солнце — идеальный шар, можно воспользоваться формулой закона сохранения момента импульса для решения этой задачи. Нужно перевести сутки в секунды и километры в метры, получается:

L = I*ω = 2/5*m*r12*ω1 = 2/5*m*r22*ω2.

ω2 = (r1/r2)2*ω1 = (696000000/7000000)2*2*3,1416/(25,4*24*3600)= 0,0283 рад/с.

Здесь использовалась формула для угловой скорости (ω = 2*pi/T, где T — период вращения в секундах). При выполнении вычислений также было сделано предположение, что масса Солнца остается постоянной (это не верно, поскольку она будет уменьшаться. Тем не менее полученное значение ω2 является нижней границей, то есть в действительности Солнце-карлик будет вращаться еще быстрее).

Поскольку полный оборот — это 2*pi радиан, тогда получится:

T2 = 2*pi/ω2 = 222 с.

То есть в конце своего жизненного цикла данная звезда будет делать один оборот вокруг своей оси быстрее, чем за 222 секунды.

Электронная библиотека

Моментом импульса материальной точки относительно неподвижной точки ( ) называется физическая величина, определяемая векторным произведением:

где -радиус-вектор, проведенный из точки О в точку А; — импульс материальной точки (рис. 4.4); – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

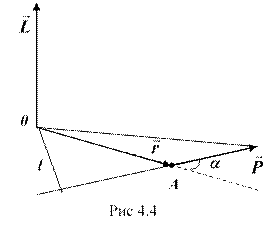
Модуль вектора момента импульса равен:

где – угол между векторами и ; – плечо вектора относительно точки O.

Моментом импульса относительно неподвижной оси (z) называется скалярная величина ( ), равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки (О) данной оси. Момент импульса ( ) не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, то есть радиус является плечом вектора . Поэтому можем записать, что момент импульса отдельной частицы равен: и направлен по оси в сторону, определяемую правилом правого винта.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцировав уравнение (4.1) по времени получим:

Это выражение есть еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. Физический смысл этого выражения: скорость изменения момента импульса равна моменту сил.

В векторной форме это можно записать так:

В замкнутой системе момент ( ) внешних сил равен нулю и, следовательно, , откуда

Выражение (4.2) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы не изменяется с течением времени. Закон сохранения момента импульса – фундаментальный закон природы.

Он связан со свойством симметрии пространства – его изотропностью, то есть с инвариантностью физических законов относительно выбора направления осей координат системы отсчета. Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение: