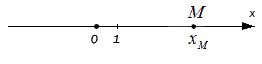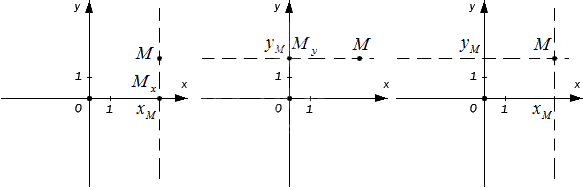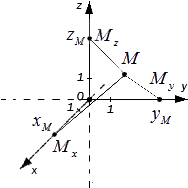Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей
В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.
Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.
По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.
Уравнения двух плоскостей, задающих прямую линию в пространстве
Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.
Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:
n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R
Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.
Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .
Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.
Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .
Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости
Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .
Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .
Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.
Рассмотрим решение примера
Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x — 2 y + z — 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , — 1 , 0 ) и N 0 ( 0 , — 1 3 , 1 ) прямой линии пересечения плоскостей.
Решение
Начнем с точки М 0 . Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( — 1 ) + 1 = 0 1 — 2 · ( — 1 ) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0 .
В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.
Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , — 1 3 , 1 ) . Получаем 2 · 0 + 3 · — 1 3 + 1 = 0 0 — 2 · — 1 3 + 1 — 3 = 0 ⇔ 0 = 0 — 1 1 3 = 0 .
Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.
Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.
Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.
Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.
Решение
Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 .
Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.
Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:
x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 ⇔ x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z
Введем произвольное действительное число λ и примем, что z = λ .
Тогда x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z ⇔ x + 0 y = — 7 — 3 λ 2 x + 3 y = — 2 — 3 λ .
Для решения полученной системы уравнений применим метод Крамера:
∆ = 1 0 2 3 = 1 · 3 — 0 · 1 = 2 ∆ x = — 7 — 3 λ 0 — — 3 λ 3 = — 7 — 3 λ · 3 — 0 · ( — 2 — 3 λ ) = 21 — 9 λ ⇒ x = ∆ x ∆ = — 7 — 3 λ ∆ y = 1 — 7 — 3 λ 2 — 2 — 3 λ = 1 · — 2 — 3 λ — — 7 — 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ
Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = — 7 — 3 λ y = 4 + λ z = λ , где λ ∈ R .
Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = — 7 — 3 · 0 y = 4 + 0 z = 0 ⇔ x = — 7 y = 4 z = 0 .
Это позволяет нам получить координаты искомой точки — 7 , 4 , 0 .
Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей — 7 + 3 · 0 + 7 = 0 2 · ( — 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .
Ответ: — 7 , 4 , 0
Направляющий вектор прямой, по которой пересекаются две плоскости
Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.
Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.
Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .
Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .
a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2
Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ — это параметр, который может принимать любые действительные значения, отличные от нуля.
Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y — 3 z — 2 = 0 x — z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.
Решение
Плоскости x + 2 y — 3 z — 2 = 0 и x — z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , — 3 и n 2 → = 1 , 0 , — 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:
a → = n → 1 × n 2 → = i → j → k → 1 2 — 3 1 0 — 1 = i → · 2 · ( — 1 ) + j → · ( — 3 ) · 1 + k → · 1 · 0 — — k → · 2 · 1 — j → · 1 · ( — 1 ) — i → · ( — 3 ) · 0 = — 2 · i → — 2 j → — 2 k →
Запишем ответ в координатной форме a → = — 2 , — 2 , — 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».
Ответ: a → = — 2 , — 2 , — 2
Переход к параметрическим и каноническим уравнениям прямой в пространстве
Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z — координаты направляющего вектора прямой, x 1 , y 1 , z 1 — координаты некоторой точки прямой, а λ — параметр, принимающий произвольные действительные значения.
От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.
Рассмотрим написанное выше на примере.
Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.
Решение
Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , — 1 плоскости 2 x + y — z — 1 = 0 и n 2 → = ( 1 , 3 , — 2 ) плоскости x + 3 y — 2 z = 0 :
a → = n 1 → × n 2 → = i → j → k → 2 1 — 1 1 3 — 2 = i → · 1 · ( — 2 ) + j → · ( — 1 ) · 1 + k → · 2 · 3 — — k → · 1 · 1 — j → · 2 · ( — 2 ) — i → · ( — 1 ) · 3 = i → + 3 · j → + 5 · k →
Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .
Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ 2 x + y — z = 1 x + 3 y — 2 z = 0 .
Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 — 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :
2 x + y — z = 1 x + 3 y — 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R
Применяем для решения полученной системы уравнений метод Крамера:
∆ = 2 1 1 3 = 2 · 3 — 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 — 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ — ( 1 + λ ) · 1 = — 1 + 3 λ ⇒ y = ∆ y ∆ = — 1 + 3 λ 5 = — 1 5 + 3 5 · λ
Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 y = — 1 5 + 3 5 z = λ
Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = — 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Ответ: x — 1 1 = y — 1 3 = z — 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Данная задача имеет еще один способ решения.
Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .
Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z
Применим данный способ к решению задачи.
Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.
Решение
Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ .
Это параметрические уравнения прямой в пространстве.
Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ ⇔ λ = x — 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x — 3 5 1 5 = y + 1 5 3 5 = z 1
Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.
Ответ: x — 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ
Как определить координаты точки в пространстве
Положение точки в пространстве представим с помощью пространственного макета. Пусть даны в пространстве точка A и три взаимно перпендикулярные плоскости проекции.
Построим проекции точки А, расположенной в первом октанте пространства. Для этого через точку проведем проецирующие лучи, идущие перпендикулярно плоскостям проекций . На пересечении этих лучей с плоскостями проекций H, V, W находятся проекции самой точки А (A`, A», A»`).
Положение точки в пространстве определяется тремя координатами (x, y, z), показывающими величины расстояний, на которые она удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно через точку A провести прямые, перпендикулярные к плоскостям проекций, определить точки A`, A», A»` встречи этих прямых с плоскостями проекций и измерить величины отрезков [AA`], [AA»], [AA»`], которые укажут соответственно значение аппликаты z, ординаты y, абсциссы x точки A.
Точки A`, A», A»` называют ортогональными проекциями точки A, при этом согласно принятым обозначениям: A` – горизонтальная проекция точки A; A» – фронтальная проекция точки A; A»` – профильная проекция точки A.
Прямые (AA` ⊥ H), (AA» ⊥ V), (AA»` ⊥ W) называют проецирующими прямыми или проецирующими лучами. Прямую (AA`), проецирующую точку A на горизонтальную плоскость проекций, называют горизонтально проецирующей прямой (лучом). Прямую (AA») проецирующую точку A на фронтальную плоскость проекций называют фронтально проецирующей прямой (лучом). Прямую (AA»`) проецирующую точку A на профильную плоскость проекций называют профильно-проецирующей прямой (лучом). Две проецирующие прямые, проходящие через точку A, определяют плоскость, которую принято называть проецирующей.
Чтобы получить эпюр точки A, выполним преобразование пространственного макета в эпюр Монжа: – фронтальная проекция точки A остается на месте, как принадлежащая плоскости V, которая не меняет своего положения при рассматриваемом преобразовании. – горизонтальная проекция A` вместе с горизонтальной плоскостью проекции опустится вниз и расположится на одном перпендикуляре к оси x с фронтальной проекцией A». – профильная проекция AA»` будет вращаться вместе с профильной плоскостью проекции и к концу преобразования займет положение, указанное на рисунке. При этом AA»` будет принадлежать перпендикуляру к оси z, проведенному через A» и удалена от оси z на такое же расстояние, на какое горизонтальная проекция A` удалена от оси x.
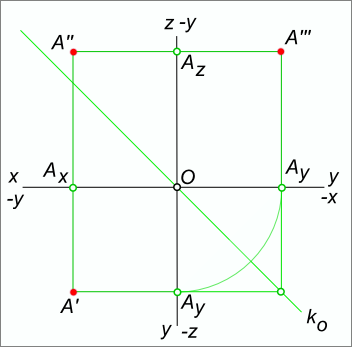
Связь между горизонтальной и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков [A`Ay] и [AyA»`] и сопрягающей их дуги окружности, с центром в точке пересечения координатных осей. Отмеченной связью пользуются для нахождения недостающей профильной или горизонтальной проекции.
Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено и без проведения дуги окружности. В этом случае связь между горизонтальной и профильной проекциями может быть установлена с помощью ломаной линии A`,Ao,A»` с вершиной Ao на биссектрисе угла, образованного осями y. Биссектрису O,Ao,A»` называют постоянной прямой ko эпюра Монжа.
Представленная на рисунке плоская модель (эпюр) несет такую же информацию, какая содержится в пространственном макете. Действительно: чтобы определить положение точки в пространстве, необходимо знать три координаты точки A – (x, y, z) – это длины отрезков [AA»`], [AA»], [AA`]. Величины этих отрезков могут быть легко определены на эпюре: [AA»`] ≅ [A`Ay] ≅ [A»Az]; [AA»] ≅ [A`Ax] ≅ [A»`Az]; [AA`] ≅ [A»Ax] ≅ [A»`Ay].
Горизонтальная проекция точки A определяется абсциссой x и ординатой y Фронтальная проекция – абсциссой x и аппликатой z Профильная проекция – ординатой y и аппликатой z
Из записи следует: 1. Точка в пространстве удалена: а) от плоскости проекции W на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси y (или же фронтальная проекция A» от оси z); б) от плоскости проекции V на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси x (или ее профильная проекция A»` от оси z); в) от плоскости проекции H на такую же величину, на какую ее фронтальная проекция A» удалена от оси x (или ее профильная проекция A»` от оси y).
2. Положение точки в пространстве вполне определяется положением ее двух ортогональных проекций. Как следствие из этого – по двум любым заданным ортогональным проекциям точки всегда можно построить недостающую ее третью ортогональную проекцию. Действительно: какое бы сочетание из двух ортогональных проекций мы не взяли, они всегда дают нам значение всех трех координат точки. 3. a) горизонтальная и фронтальная проекции любой точки принадлежат одному перпендикуляру к оси x.
Если принять во внимание, что на эпюре прямые, перпендикулярные к осям проекций и соединяющие разноименные проекции точек, называют линиями связи (проекционной связи), то пункт 3. а) может быть сформулирован иначе: горизонтальная и фронтальная проекции любой точки принадлежат одной линии связи.
б) горизонтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси y; в) фронтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси z.
Урок 1. Геометрия 11 класс
Конспект урока «Прямоугольная система координат в пространстве»
Вы уже знакомы с прямоугольной системой координат на плоскости, другими словами прямоугольной координатной плоскостью. Такую систему координат задают две взаимно перпендикулярные прямые, на каждой из которых выбрано направление и величина единичного отрезка. Эти прямые называют осями абсцисс и ординат.
Точку пересечения осей называют точкой начала координат.
Прямоугольную систему координат на плоскости обозначают Оху.
Каждой точке плоскости сопоставляется только одна пара чисел, которые называют её координатами. Для определения координат, из точки нужно провести перпендикуляры к осям, тем самым мы и получим абсциссу и ординату точки.
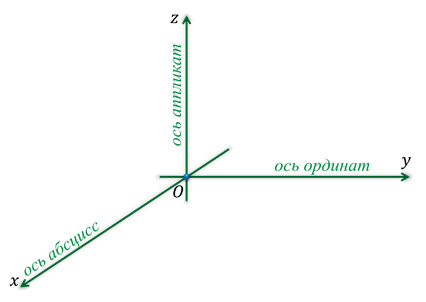
Если же через точку пространства проведены три попарно перпендикулярные прямые, а на каждой из них выбрано направление и единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называют осями координат, а точку их пересечения — началом координат. Как и на плоскости её обычно обозначают буквой О.
Оси координат обозначают так: Ох, Оу, Оz. И называют осью абсцисс, осью ординат и, новым является название третьей оси, ось аппликат.
Прямоугольную систему координат в пространстве обозначают Охуz.
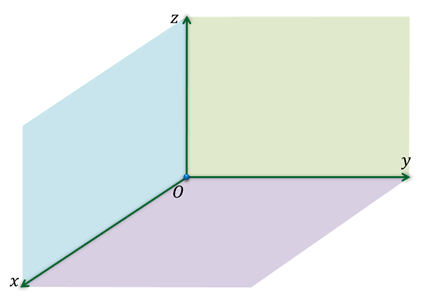
Через каждые 2 оси координат проходят координатные плоскости: Оху, Оуz и Охz. Всего таких плоскостей 3.
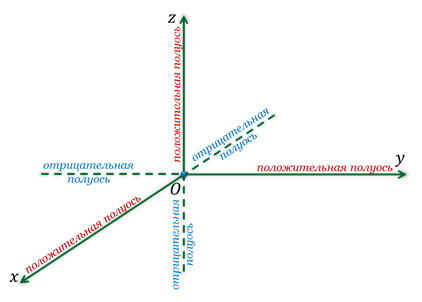
Каждая ось делится точкой О на два луча. В соответствии с этим, лучи, направление которых совпадает с направлением оси, называют положительными полуосями, а оставшиеся лучи — отрицательными полуосями.
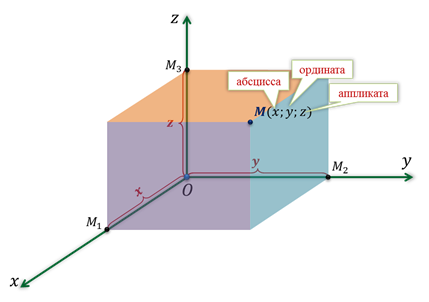
Каждой точке пространства сопоставляется только одна тройка чисел, которые называют её координатами. Их определяют аналогично тому, как это делали на плоскости. Только через точку М проводят плоскости перпендикулярные координатным осям.
Точки пересечения проведённых плоскостей с осями координат назовём М1, М2 и М3.
Первая координата точки М, то есть её абсцисса, равна длине отрезка ОМ1.
Вторая координата, которую называют ординатой, равна длине отрезка ОМ2.
Ну, а третья координата, а точнее аппликата, равна длине отрезка ОМ3.
Координаты точки записывают в скобках, при этом первой записывают абсциссу, второй — ординату, а третьей — аппликату.
В данном случае точки М1, М2 и М3 являются точками положительных полуосей, поэтому и координаты точки М будут положительными числами.
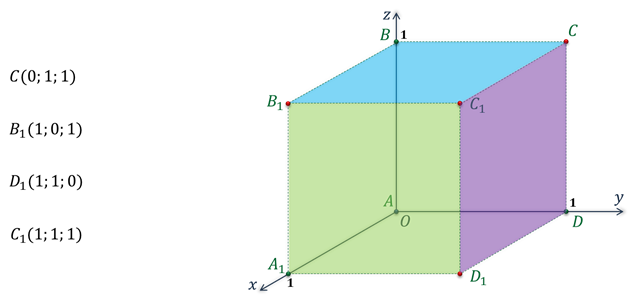
Рассмотрим примеры различного расположения точек в прямоугольной системе координат.
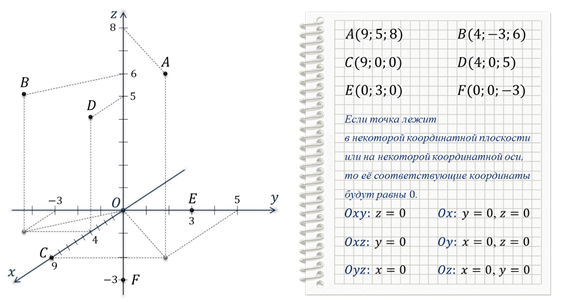
Задание: определить координаты точек А, В, С, D, Е и F.
После выполнения этого задания можно сделать вывод о том, что если точка лежит в некоторой координатной плоскости или на некоторой координатной оси, то её соответствующие координаты будут равны нулю.
Так если точка лежит в координатной плоскости ОИксИгрек, то её аппликата равна нулю. Если точка лежит в координатной плоскости ОИксЗэт, то её ордината равна нулю. И если точка лежит в координатной плоскости ОИгрекЗэт, то её абсцисса равна нулю.
Ну, а в случаях, когда точка лежит на одной из осей, только одна координата является ненулевой.
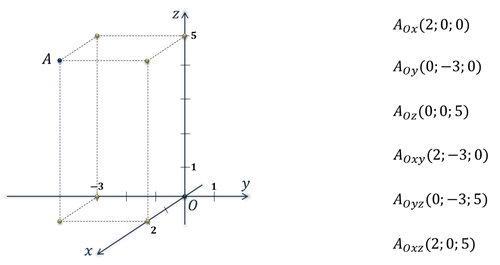
Задание: найти координаты проекций точки ��(2;−3;5) на каждую из координатных плоскостей и на каждую из координатных осей.
Далее найдём координаты проекций точки А на координатные плоскости.
Проекцией точки А на координатную плоскость Оху является основание перпендикуляра, проведённого из точки А к данной координатной плоскости. При этом координаты полученной проекции будут такими же как у точки А, только аппликата станет равной нулю.
Аналогично получим проекцию точки А на координатную плоскость Оуz. Проведём перпендикуляр из данной точки к данной координатной плоскости. Его основание и является проекцией точки А на плоскость Оуz. Координаты данной проекции равны координатам точки А, только абсцисса равна нулю.
Ну, а проекция точки А на координатную плоскость Охz будет иметь координаты 2, 0, 5.
Так мы с вами нашли координаты проекций точки А на координатные оси и на координатные плоскости.
Решение: Изобразим прямоугольную систему координат. Отметим точки, являющиеся вершинами куба, координаты которых известны.
На этом уроке вы познакомились с понятием прямоугольной системы координат в пространстве. Узнали, что её задают три взаимно перпендикулярные прямые, на которых выбраны направления и единичные отрезки. Эти прямые называют координатными осями. Точку пересечения осей называют точкой начала координат.
Ось Ох называют осью абсцисс, ось Оу называют осью ординат, и новым для вас является название оси Оz — ось аппликат. Помимо осей координат в прямоугольной системе координат присутствуют и координатные плоскости: Оху, Оуz и Охz.
Всю прямоугольную систему координат в пространстве обозначают Охуz.
Любой точке пространства соответствует только одна тройка чисел х, у и z, которые и являются её координатами. Все координаты точки О начала координат равны нулю.
При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.
Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.
Прямоугольная декартова система координат на плоскости
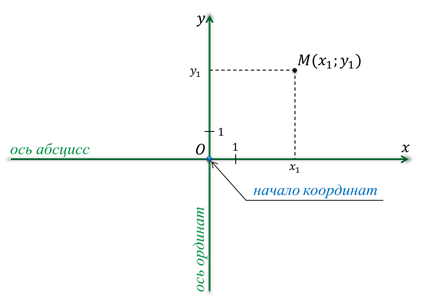
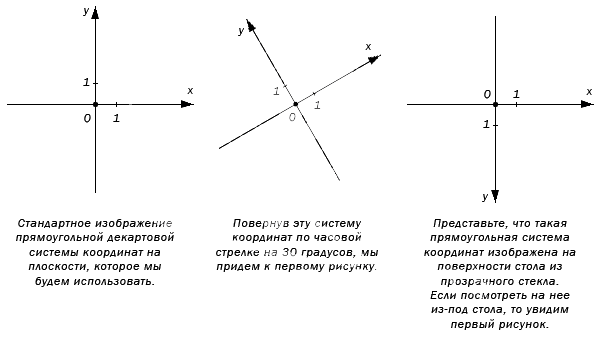
Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O . Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.
Прямые с началом O , имеющие направление и масштаб, называют координатной прямой или координатной осью.
Прямоугольная система координат обозначается O x y . Координатными осями называют О х и О у , называемые соответственно ось абсцисс и ось ординат.
Изображение прямоугольной системы координат на плоскости.
Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.
Прямоугольная система координат в трехмерном пространстве
Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех О х , О у , О z осей. Это три взаимно перпендикулярные прямые, где О z имеет название ось аппликат.
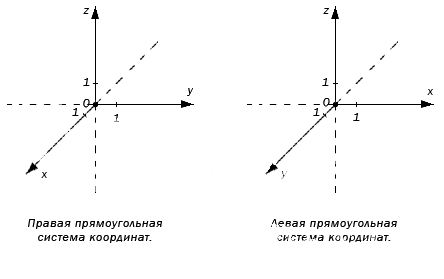
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке O , называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте О х против часовой стрелки на 90 ° ее положительное направление совпадает с положительным О у , тогда это применимо для положительного направления О z . Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y , а средний за Z .
Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат на плоскости
Для начала отложим точку М на координатной оси О х . Любое действительное число x M равняется единственной точке М , расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если – 3 , то соответственное расстояние 3 . Ноль – это начало отсчета координатных прямых.
Иначе говоря, каждая точка М , расположенная на O x , равна действительному числу x M . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении O x и О у . Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.
Имеющееся число x M называют координатой точки М на заданной координатной прямой.
Возьмем точку как проекцию точки M x на О х , а как проекцию точки M y на О у . Значит, через точку М можно провести перпендикулярные осям О x и О у прямые, где послучим соответственные точки пересечения M x и M y .
Тогда точка M x на оси О х имеет соответствующее число x M , а M y на О у – y M . На координатных осях это выглядит так:
Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел ( x M , y M ) , называемую ее координатами. Абсцисса M – это x M , ордината M – это y M .
Обратное утверждение также считается верным: каждая упорядоченная пара ( x M , y M ) имеет соответствующую заданную в плоскости точку.
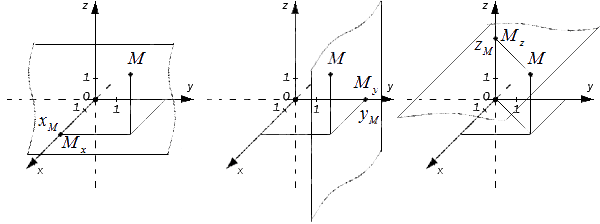
Координаты точки в прямоугольной системе координат в трехмерном пространстве
Определение точки М в трехмерном пространстве. Пусть имеются M x , M y , M z , являющиеся проекциями точки М на соответствующие оси О х , О у , О z . Тогда значения этих точек на осях О х , О у , О z примут значения x M , y M , z M . Изобразим это на координатных прямых.
Чтобы получить проекции точки M , необходимо добавить перпендикулярные прямые О х , О у , О z продолжить и изобразит в виде плоскостей, которые проходят через M . Таким образом, плоскости пересекутся в M x , M y , M z
Каждая точка трехмерного пространства имеет свои данные ( x M , y M , z M ) , которые имеют название координаты точки M , , x M , y M , z M – это числа, называемые абсциссой, ординатой и аппликатой заданной точки M . Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел ( x M , y M , z M ) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.
Точка пересечения прямых в пространстве онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых в пространстве. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический» или «параметрический» ), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Точка пересечения прямых в пространстве − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в каноническом виде.
- 2. Точка пересечения прямых, заданных в параметрическом виде.
- 3. Точка пересечения прямых, заданных в разных видах.
- 4. Примеры нахождения точки пересечения прямых в пространстве.
1. Точка пересечения прямых в пространстве, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2:
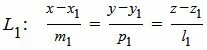 , , | (1) |
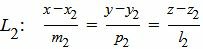 , , | (2) |
Найти точку пересечения прямых L1 и L2 (Рис.1).
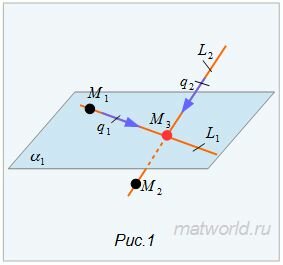 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
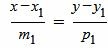 , , | (3) |
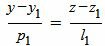 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Аналогичным образом преобразуем уравнение (2):
Запишем уравнение (2) в виде системы двух линейных уравнений:
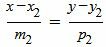 , , | (7) |
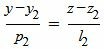 | (8) |
Сделаем перекрестное умножение в уравнениях (7) и (8):
| p2(x−x2)=m2(y−y2) |
| l2(y−y2)=p2(z−z2) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p2x−m2y=p2x2−m2y2, | (9) |
| l2y−p2z=l2y2−p2z2. | (10) |
Решим систему линейных уравнений (5), (6), (9), (10) с тремя неизвестными x, y, z. Для этого представим эту систему в матричном виде:
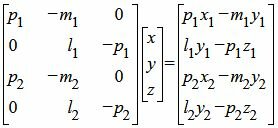 | (11) |
Как решить систему линейных уравнений (11)(или (5), (6), (9), (10)) посмотрите на странице Метод Гаусса онлайн. Если система линейных уравнениий (11) несовместна, то прямые L1 и L2 не пересекаются. Если система (11) имеет множество решений, то прямые L1 и L2 совпадают. Единственное решение системы линейных уравнений (11) указывает на то, что это решение определяет координаты точки пересечения прямых L1 и L2 .
2. Точка пересечения прямых в пространстве, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
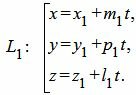 | (12) |
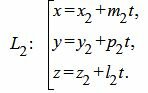 | (13) |
Задачу нахождения нахождения точки пересечения прямых L1 и L2 можно решить разными методами.
Метод 1. Приведем уравнения прямых L1 и L2 к каноническому виду.
Для приведения уравнения (12) к каноническому виду, выразим параметр t через остальные переменные:
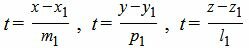 | (14) |
Так как левые части уравнений (14) равны, то можем записать:
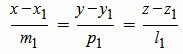 | (15) |
Аналогичным образом приведем уравнение прямой L2 к каноническому виду:
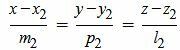 | (16) |
Далее, для нахождения точки пересечения прямых, заданных в каноническом виде нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямых L1 и L2 решим совместно уравнения (12) и (13). Из уравнений (12) и (13) следует:
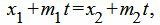 | (17) |
 | (18) |
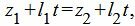 | (19) |
Из каждого уравнения (17),(18),(19) находим переменную t. Далее из полученных значений t выбираем те, которые удовлетворяют всем уравнениям (17)−(19). Если такое значение t не существует, то прямые не пересекаются. Если таких значений больше одного, то прямые совпадают. Если же такое значение t единственно, то подставляя это зачение t в (12) или в (13), получим координаты точки пересечения прямых (12) и (13).
3. Точка пересечения прямых в пространстве, заданных в разных видах.
Если уравнения прямых заданы в разных видах, то можно их привести к одному виду (к каноническому или к параметрическому) и найти точку пересечения прямых, описанных выше.
4. Примеры нахождения точки пересечения прямых в пространстве.
Пример 1. Найти точку пересечения прямых L1 и L2:
 | (20) |
 | (21) |
Представим уравнение (20) в виде двух уравнений:
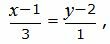 | (22) |
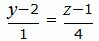 | (23) |
Сделаем перекрестное умножение в уравнениях (22) и (23):
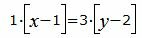 |
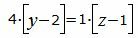 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
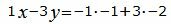 |
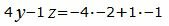 |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
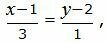 | (26) |
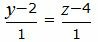 | (27) |
Сделаем перекрестное умножение в уравнениях (7) и (8)
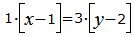 |
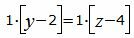 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
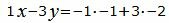 |
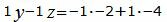 |
Решим систему линейных уравнений (24), (25), (28), (29) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
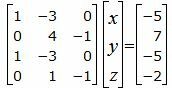 | (30) |
Решим систему линейных уравнений (30) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
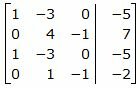 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1:
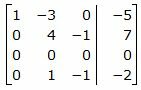 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 4 со строкой 2, умноженной на −1/4:
 |
Сделаем перестановку строк 3 и 4.
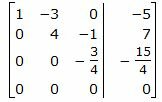 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −4/3:
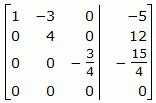 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 3/4:
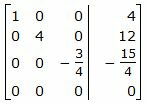 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
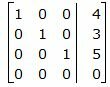 |
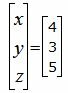 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
 | (31) |
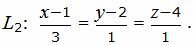 | (32) |
Приведем параметрическое уравнение прямой L1 к каноническому виду. Выразим параметр t через остальные переменные:
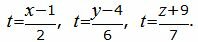 |
Из равентсв выше получим каноническое уравнение прямой:
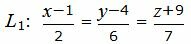 | (33) |
Представим уравнение (33) в виде двух уравнений:
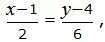 | (34) |
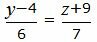 | (35) |
Сделаем перекрестное умножение в уравнениях (34 и (35):
 |
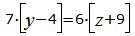 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
 |
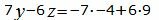 |
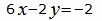 | (36) |
 . . | (37) |
Аналогичным образом поступим и с уравнением (2).
Представим уравнение (2) в виде двух уравнений:
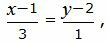 | (38) |
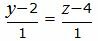 | (39) |
Сделаем перекрестное умножение в уравнениях (38) и (39)
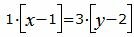 |
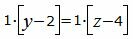 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
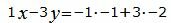 |
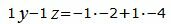 |
Решим систему линейных уравнений (36), (37), (40), (41) с тремя неизвестными x, y, z. Для этого представим эту систему в виде матричного уравнения:
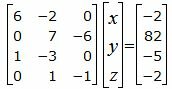 | (42) |
Решим систему линейных уравнений (42) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −1/6:
 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строки 3 и 4 со строкой 2, умноженной на 8/21 и −1/7, соответственно:
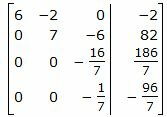 |
Исключим элементы 3-го столбца матрицы ниже элементаa33. Для этого сложим строку 4 со строкой 3, умноженной на -1/16:
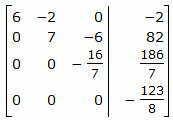 |
Из расширенной матрицы восстановим последнюю систему линейных уравнений:
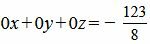 | (43) |
Уравнение (43) несовместна, так как несуществуют числа x, y, z удовлетворяющие уравнению (43). Следовательно система линейных уравнений (42) не имеет решения. Тогда прямые L1 и L2 не пересекаются. То есть они или параллельны, или скрещиваются.
Прямая L1 имеет направляющий вектор q1=<2,6,7>, а прямая L2 имеет направляющий вектор q2=<3,1,1>. Эти векторы не коллинеарны. Следовательно прямые L1 и L2 скрещиваются .
http://4systems.ru/inf/kak-opredelit-koordinaty-tochki-v-prostranstve/
http://matworld.ru/analytic-geometry/tochka-peresechenija-prjamyh-3d.php