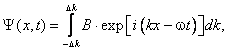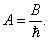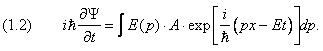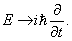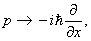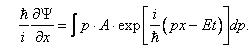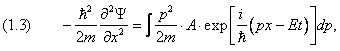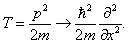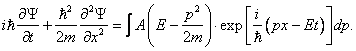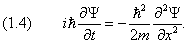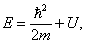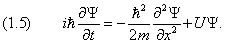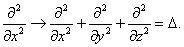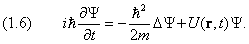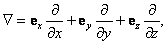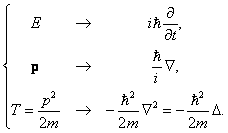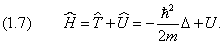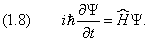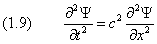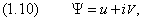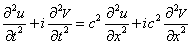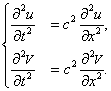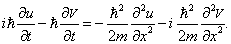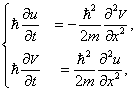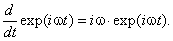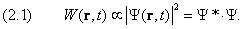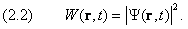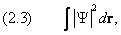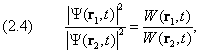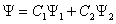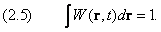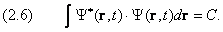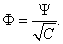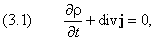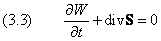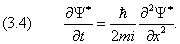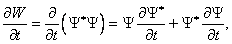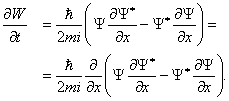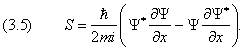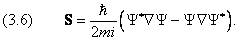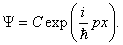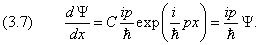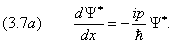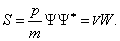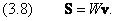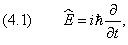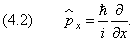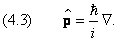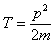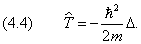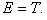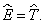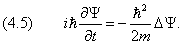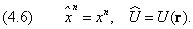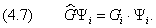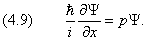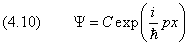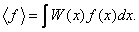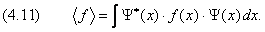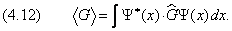Плотность вероятности и плотность потока вероятности
Вы будете перенаправлены на Автор24
Плотность вероятности
В квантовой механике состояние микрочастиц описывают при помощи волновой функции $\Psi(\overrightarrow
где величина равная:
называется плотностью вероятности. Она определяет вероятность того, что частица находится в единичном объеме в окрестности точки ($x,y,z$). Физический смысл имеет не сама волновая функция, квадрат ее модуля ($<\left|\Psi\right|>^2$).
Вероятность найти частицу в момент времени t в конечном объеме V по теореме о сложении вероятности равна:
Так как величина $<\left|\Psi\right|>^2dV$ определена как вероятность, волновую функцию следует нормировать. Вероятность достоверного события должна быть равна единице, если в качестве объема ($V=\infty )$ принимать все пространство. Это означает, что при данном условии частица находится в пространстве, где — либо. Условие нормировки вероятности записывается как:
Интеграл в выражении (1) вычисляется по всему пространству. Условие (4) отражает факт объективного существования частицы во времени и пространстве.
Так, например, величина $<\left|\Psi(x)\right|>^2$ определяет плотность вероятности нахождения частицы в точке $x$ для одномерного движения. Следовательно, среднее значение координаты частицы можно найти как:
Плотность потока вероятности
Найдем производную по времени ($\frac
В классической физике функцией Гамильтона ($H\left(\overrightarrow
\right)$) называют полную энергию, которая выражена через импульсы и координаты частицы. Для одной частицы полная энергия равна:
В квантовой механике функции Гамильтона соответствует оператор. Он получится, если в выражение (7) вместо вектора импульса подставить оператор $\hat
$, равный:
Используя выражение (9), запишем:
Получаем, применяя (10):
где вектор $\overrightarrow
Готовые работы на аналогичную тему
По теореме Гаусса имеем:
Из выражения (15) видно, что вектор $\overrightarrow
Уравнение (16) можно назвать аналогом уравнения непрерывности в классической физике.
Задание: Собственная волновая функция частицы, которая находится в бесконечно глубоком одномерном потенциальном ящике, равна: $\Psi\left(x\right)=\sqrt<\frac<2>
Решение:
Вероятность ($dP$) нахождения частицы в интервале $dx$ определим, используя плотность вероятности $<\left|\Psi\right|>^2$ и выражение (для одномерного случая):
Следовательно, сама вероятность будет найдена как:
Если частица находится в основном состоянии, то для нее $n=1$. Используем волновую функцию, заданную в условиях, подставим ее в интеграл (1.2), получим:
Применим тригонометрическую формулу:
Вычислим интеграл (1.3), получаем:
Ответ: $P=0,195.$
Решение:
Используем формулу, для вычисления среднего значения величины, через плотность вероятности:
где $dV=4\pi r^2dr-\ $сферический слой с радиусами $r$ и $r+dr$.
В интеграл (2.1) подставим $<\left|\Psi\left(r\right)\right|>^2$, возьмем интеграл по частям, имеем:
Ответ: $\left\langle r\right\rangle =\frac<2>$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 06 05 2021
Вероятность в квантовой механике. Откуда она взялась и как это упростить для понимания
Введение
Эта статья рассчитана на людей, имеющих начальные знания по квантовой механике, обычно входящей в вузовский курс теоретической физики, а также живой интерес к ней. Квантовая механика, как матанализ, требует определенных начальных знаний, и без этого любое чтение будет либо беллетристикой, либо приведет к неправильным представлениям. Все обещания квантовой механики для всех и даром сродни социалистическим предвыборным лозунгам. Тем не менее эти необходимые знания не так велики, как может показаться, особенно для знающих математику. В начале изучения у многих возникает проблема — вероятностный смысл волновой функции и связанные с этим вещи: процесс измерения и гипотеза редукции волновой функции, трудны для понимания. Тем более, что в дальнейшем при решении задач этот вероятностный смысл или интерпретация, как правило, не требуются, поэтому многие даже не задумываются над этим. Тем не менее хотелось бы разобраться, откуда это взялось и зачем вообще нужно, и нужно ли вообще. Оказывается, что соображения, которые, вероятно, легли в основу столь сложных и противоречивых постулатов, утратили силу по мере прогресса квантовой электродинамики. Глубоких знаний для понимания не потребуется — можно просто поверить хорошо известным результатам из учебников, но начальный уровень все же необходим.
По проблеме интерпретации волновой функции споры велись с самого начала разработки квантовой механики. Наиболее известный – дискуссия Бора и Эйнштейна, длившаяся много лет. Интерпретация волновой функции, как амплитуды вероятности, разработана, в-основном, Борном [1] и дополнена Бором и Гейзенбергом [2] — физиками «Копенгагенской школы». В дальнейшем в литературе было принято название «Копенгагенская интерпретация», далее КИ. Я использую стандартные обозначения, принятые в «Курсе теоретической физики» Л.Д.Ландау и Е.М.Лифшица [3] и в большинстве других аналогичных учебников. Во второй части статьи предлагаются критические эксперименты, которые могли бы опровергнуть или подтвердить КИ. К сожалению, они неосуществимы технически в наше время.
Вероятностная интерпретация
В КИ постулируется, что волновая функция 
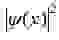
В настоящее время классическая борновская интерпретация претерпела изрядную ревизию, так многих не устраивает ни понятие измерения, ни загадочная редукция. Появилось довольно много работ на эту тему. Однако, следование борновской или какой-то другой интерпретации не влияет на методы решения задач в теории и на получаемые математические результаты. Поэтому эти работы больше похожи на философские или популяризаторские, к серьезной теоретической физике их трудно отнести. Например, многомировая интерпретация, предложенная в 1957 г. Эвереттом [4], обсуждаемая в [5], вводит множество вариантов реальностей, из которых неведомо как делается выбор. Вводятся новые категории, которые более нигде не используются. Такое количество различных версий позволяет предположить, что ни одна не является хорошо обоснованной. Вместе с тем именно непонятная интерпретация сильно затрудняет изучение квантовой механики на начальном этапе. Существует аксиоматическое изложение квантовой теории [6], где вообще отсутствует физическая интерпретация вектора состояния. Это удобно для математика, но для начинающего физика не годится.
Все имеющиеся работы не дают ответа на простой вопрос: «Что заставило в 20е годы XX века множество первоклассных талантов придти к такой спорной трактовке и вводить понятия, не определенные хотя бы на физическом уровне строгости — измерение, классический прибор, и гипотезу редукции волновой функции, не подкрепленную весомыми аргументами». Чтобы разобраться, надо вспомнить, что в эти годы в квантовой механике был только один тип взаимодействия — электромагнитное поле, а основной тип объектов — электроны.
В классической теории поля тоже есть вспомогательные понятия — пробный заряд или рамка с током. Но они нужны, чтобы пояснить физический смысл вводимых напряженностей поля и потенциалов. Последовательная и логичная теория строится и без них, на основе лагранжиана поля и зарядов. Так как к квантовой механике приступают, уже освоив теорию поля, у новичка возникает вопрос — а нужна ли вообще эта вероятностная интерпретация? Чем плоха точка зрения Эйнштейна, который считал частицы просто состояниями полей? Давайте забудем о классических частицах и будем просто рассматривать поле 

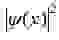
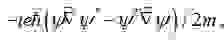



Какие аргументы были у копенгагенской школы в пользу КИ?
КИ тоже позволяет интерпретировать ряд экспериментов, например, по дифракции электронов. Но эксперименты чисто качественные — рассматривалось [7] почернение фотопластинки. В принципе можно рассмотреть простейшую модель детектора, состоящую из 

Один из основных аргументов Борна состоял в том, что, согласно уравнению Шредингера, волновой пакет микроскопической частицы неограниченно размывается со временем. Это казалось ему абсурдным. Однако в конденсате Бозе — Эйнштейна каждая частица размазана по всему макроскопическому образцу, так что аргумент Борна некорректен. Должны быть другие аргументы против простейшей полевой интерпретации 
Действительно, можно просто ввести комплексное поле 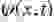

Это слагаемое можно вывести также, как энергию электромагнитного поля электронного облака в пренебрежении токами. Для атома водорода такое слагаемое того же порядка, что и взаимодействие с ядром, то есть хорошо известный и проверенный экспериментально спектр изменился бы кардинально. Мало того, даже для свободного электрона возникают абсурдные следствия — кулоновское отталкивание приводит к разлету волнового пакета и размазыванию электронного облака по всему доступному пространству. Ничего подобного в эксперименте не наблюдается. Наверное, именно это и привело копенгагенскую школу к КИ, так как все вышеизложенные простые соображения, вероятно, приходили им в голову. Действительно, для точечной частицы такое слагаемое отсутствует, точнее, сводится к постоянной. Далее, для атома гелия учет кулоновского взаимодействия двух электронов между собой дает вполне правдоподобные результаты, что опять-таки соответствует концепции точечных частиц. То есть КИ появилась за неимением лучшего. Но в нерелятивистской квантовой механике частицы не возникают и не исчезают. Тогда утверждение о том, что электрон находится в одной точке, противоречит экспериментам с дифракцией одного электрона на 2 щелях. Кроме того, в упоминавшемся [7] эксперименте наблюдали интерференцию на кристалле одного электрона. Так что просто и логично объяснить на основе КИ и уравнение Шредингера, и известные эксперименты не представляется возможным. В результате был придуман некий алгоритм, который в одних случаях предписывает считать электрон частицей, а в других — волной, и назван КИ с добавкой «корпускулярно-волновой дуализм». В то же время и обычная полевая интерпретация 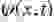
На самом деле при написании (1) было неявно сделано одно недоказанное допущение – электроны взаимодействуют с классическим электромагнитным полем. Можно ли считать электромагнитное поле электрона классическим? Чтобы разобраться, надо использовать квантовую электродинамику. Ведь на самом деле нет никакого кулоновского потенциала, а есть электромагнитное поле, взаимодействующее с электронами. При этом электромагнитное поле, входящее в уравнение Шредингера или Дирака для атома водорода, принципиально иное, нежели то, которое вызывает взаимодействие между электронами. Оно классическое, то есть имеет определенное значение в каждой точке, и порождается классическим объектом — ядром.
Чтобы корректно исследовать задачу, надо перейти к релятивистской квантовой теории, тогда волновая функция становится оператором. Здесь нет необходимости (а также места) писать соответствующие формулы и вычисления, желающие найдут их в учебнике (см., например [8]). Я ограничусь изложением известных результатов. Рассмотрим для начала свободный электрон. Чтобы понять, что случится с его волновым пакетом (или облаком), надо выяснить, как меняется его гриновская функция или пропагатор из-за взаимодействия с электромагнитным полем. Поправки к гриновской функции свободного электрона, возникающие при учете взаимодействия с электромагнитным полем, написанные формально по теории возмущений, как известно, сводятся к расходящимся интегралам. Однако эта проблема была решена. Было показано, что учет взаимодействия с квантованным электромагнитным полем для свободного электрона приводит просто к замене в соответствующих формулах заряда и массы на перенормированные (наблюдаемые) величины [8]. Таким образом, в нерелятивистском случае малых импульсов учет взаимодействия одного электрона с электромагнитным полем приводит просто к обычному линейному уравнению Шредингера с перенормированными зарядом и массой вместо слагаемого (1), то есть предположение о классичности электромагнитного поля дает в этом случае принципиально неверный результат. Аналогичное решение с перенормировкой существует и для электрона во внешнем поле — оно рассматривается в теории лэмбовского сдвига для атома водорода [8,9].
Рассмотрим теперь два электрона. Для случая малых, нерелятивистских импульсов можно ввести некое эффективное взаимодействие между ними в уравнение Шредингера. Определить его вид можно по амплитуде взаимного рассеивания — она однозначно связана с взаимодействием. В диаграммной технике Фейнмана ей соответствуют диаграммы с 4-мя внешними электронными линиями. В случае малых импульсов соответствующая амплитуда рассеяния переходит в классическую формулу Резерфорда с учетом обмена [8], то есть взаимодействие между электронами в атоме действительно можно рассматривать, используя кулоновский потенциал.
Таким образом, от неприятных противоречий, вытекающих из интерпретации волновой функции, как обычного поля, без всяких корпускулярных свойств, можно избавиться, если привлечь релятивистскую квантовую теорию. Впрочем, постольку, поскольку рассматривается электромагнитное поле, это вполне логично. Во всяком случае, это намного понятнее, чем пресловутый дуализм и КИ, и близко к точке зрения Эйнштейна. В релятивистской теории 
Может возникнуть вопрос: почему же КИ не исчезла из учебников, если без нее так легко сейчас обойтись? Я показал эту статью нескольким знакомым профессорам из разных университетов и обнаружил, что этот предмет их практически не интересует. Для людей, уже глубоко освоивших теоретическую физику он неактуален. Неактуален он и для математиков, работающих в теоретической физике. Крупные ученые вообще перестали интересоваться обучением и распространением знаний в той мере, как это было лет 50 назад. Ландау был последним из великих физиков-теоретиков, кто ставил преподавание и работу с учениками наравне или выше личных результатов, но он не успел освоить новые методы квантовой электродинамики — попал в роковую аварию.
Процесс измерения, значения физической величины и стационарные состояния. Другие проблемы в понимании
Из вероятностной интерпретации (КИ) и процесса измерения, который никак не конкретизируется, вытекает еще одна путаница с вероятностями состояний и значениями какой-либо физической величины F у квантовой частицы. Утверждается, что коэффициенты разложения 
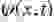





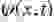

Существенную путаницу в этой области создает рассмотрение исключительно стационарных состояний, то есть собственных векторов гамильтониана. У студентов часто складывается убеждение, что других состояний вообще не бывает, а энергия принимает значения только из спектра гамильтониана. Между тем стационарные состояния — идеализация, в чистом виде редко существующая. Гораздо ближе к реальности (например, для свободных частиц) когерентные состояния, минимизирующие соотношение неопределенностей. Ограничение рассмотрения исключительно стационарными состояниями приводит к утверждению, кочующему из учебника в учебник, о том, что энергия моды электромагнитного поля с частотой 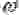
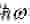


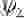

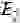

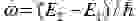

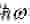
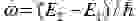
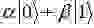
Наибольший интерес разобранная двухуровневая задача представляет применительно к спину электрона. Пусть имеется электрон в связанном состоянии со спином вдоль оси x. Прикладываем магнитное поле вдоль оси z. Тогда волновая функция электрона может быть записана в виде 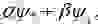


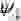
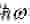
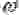
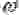
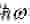

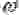
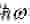

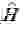
Отличить нестационарное состояние от стационарного можно было бы по импульсу отдачи электрона. Во втором случае (если отбросить КИ) он в 2 раза меньше. Для локализованного состояния электрона с энергией связи E порядка 10 -1 электрон-вольта вероятность ионизации будет в обоих случаях различной, и порог ионизации по магнитному полю будет отличаться в 2 раза. К сожалению, оценка показывает, что для ионизации нужны слишком сильные магнитные поля 10 11 гс. Такие поля в настоящее время недостижимы.
Можно было бы использовать для экспериментальной проверки свободные электроны, ориентация спина которых задана магнитным полем. Рассмотрим установку, состоящую из камеры со свободными электронами в сильном магнитном поле вдоль оси z. Электроны вылетают из отверстия в камере с магнитным полем, имея спин вдоль оси z, в камеру, где на вращающейся оси расположены 2 одинаковых диска с отверстиями, смещенными на угол φ. Такая установка позволяет получить на выходе параллельный оси x пучок электронов одинаковой энергии. Попадая в область магнитного поля, направленного вдоль оси x, электроны со спинами, ориентированными вдоль оси z, должны начать излучать фотоны частоты 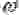
10 6 Гс импульс отдачи соответствует энергии 3*10 -11 эв или скорости порядка 3 м/с. Достаточно сложно обеспечить такую малую скорость электрона, так как она гораздо меньше тепловой.
Заключение
Полевая интерпретация 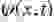
Поэтому неудивительно, что есть свидетельство племянницы Л.Д. Ландау [10], что он сам, поместивший в своем знаменитом «Курсе теоретической физики» подробное изложение КИ [3], относился к ней совершенно равнодушно:
«Моему брату, тогда студенту, Лёне Кардашинскому, по его дословным воспоминаниям, в ответ на вопрос: что такое электрон, Дау, в свойственной ему решительной манере, ответил: «Электрон не корпускула и не волна. С моей точки зрения — он уравнение, в том смысле, что лучше всего его свойства описываются уравнением квантовой механики, и прибегать к другим моделям — корпускулярной или волновой, нет никакой необходимости». ». Выводы этой статьи, в-общем, в русле мнения Ландау — не нужно никаких дополнительных концепций, постулатов и т.п. для объяснения физического смысла квантовой механики. Традиционного понятия поля 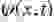
Как я уже писал выше, для специалистов этот вопрос, как правило, неактуален. Но для студентов-физиков, осваивающих материал и пытающихся понять физический смысл формул, он очень важен. Особенно сейчас, когда общий интерес к физике упал ниже плинтуса.
Если статья вызовет интерес, я могу написать продолжение, посвященное так называемой «квантовой запутанности». На самом деле это название в русскоязычных материалах происходит от безграмотности — в учебниках, например, [3] §14, эти состояния всегда называются смешанными, но авторы статей, похоже, учебников не читали. Из простых рассуждений будет понятно, почему никакой квантовой телепортации информации не существует, и почему эффектные опыты с этими состояниями малоинтересны для науки. Это эффекты «на публику», а не для специалистов.
Уравнение для плотности вероятности волновой функции
Задачи атомной физики решаются методами квантовой теории, которая принципиально отличается от классической механики.
Решение задачи о движении тела макроскопических размеров основано на применении второго закона Ньютона. Если известны силы, действующие на тело, то сначала мы находим его ускорение, затем — траекторию, после чего — все параметры движения. Но в масштабах атомов понятие траектории теряет свой смысл. Своё значение сохраняют так называемые интегралы движения. К ним относятся, в первую очередь, энергия, импульс, момент вращения и чётность. В квантовой теории эти величины определяются сразу, минуя этап вычисления траектории.
В основе расчётов лежит уравнение Шредингера. Решив его, мы находим набор энергетических уровней, который реализуется в заданном потенциале, а также получаем информацию статистического характера о возможном положении частицы.
8.1. Уравнение Шредингера
Уравнение Шредингера, как законы Ньютона и уравнения Максвелла, вывести нельзя. Оно основано на анализе экспериментальных данных и в масштабах атомов описывает волновые свойства частиц. Покажем связь уравнения Шредингера с волновым пакетом. Для этого запишем уравнение волнового пакета:
где B — амплитуда. Будем считать, что величина B как функция k равна нулю при k Δ k и k > Δ k . Тогда областью интегрирования становится вся числовая ось. Вспоминая соотношения де Бройля-Эйнштейна (формулы (2.1) и (2.1а) первой главы), приходим к новой записи выражения для волнового пакета
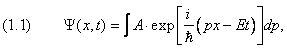
Продифференцируем (1.1) по времени:
Появлению энергии в подынтегральной функции соответствует оператор дифференцирования
Его называют оператором энергии . Импульс, в свою очередь, связан с оператором
в чём можно убедиться, дифференцируя (1.1) по x :
Мы рассматриваем нерелятивистскую частицу в отсутствие внешних полей, следовательно, ее энергия равна p2/2 m. Ей можно сопоставить оператор двойного дифференцирования по координате:
Вычитая (1.3) из (1.2), получим
Всё подынтегральное выражение вместе с разностью 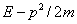
Мы вывели одномерное уравнение Шредингера для свободной частицы. Теперь учтём возможное присутствие внешних полей:
Здесь U = U( x , t ) — потенциальная энергия, зависящая только одной координаты. Вообще говоря, она может также меняться со временем. Соответственно, приходим к одномерному уравнению Шредингера:
Обобщение на случай трёх измерений сводится к замене производной по x оператором Лапласа:
Уравнение Шредингера с потенциалом, зависящим от всех трёх координат, имеет вид
Вектору импульса в трёхмерном случае соответствует оператор градиента:
где e x , e y и e z — единичные векторы в направлении координатных осей. В процессе вывода мы использовали следующие соотношения между физическими величинами и операторами:
Оператор принято отмечать «шляпкой». Например, оператор, отвечающий физической величине G, обозначается как Ĝ. В квантовой механике вводится оператор энергии, или оператор Гамильтона
Он позволяет записать уравнение Шредингера следующим образом:
Уравнение Шредингера содержит мнимую единицу i , следовательно, его решение должно быть комплексным. Этим оно отличается от волнового уравнения в классической механике . В качестве примера рассмотрим одномерный случай. Классическое уравнение
позволяет работать отдельно с действительной и мнимой частями Y , каждая из которых подчиняется одному и тому же уравнению. В самом деле, если
где u и V — действительные функции, то уравнению (1.9), которое мы теперь запишем в виде
равносильна система одинаковых уравнений, каждое из которых совпадает с исходным :
Действительная и мнимая части Y разделились. Мы убедились, что в классическом случае нет принципиальной необходимости в комплексном представлении (хотя оно часто используется для удобства вычислений). Для уравнения Шредингера это не так. Разложение (1.10) вставим теперь в уравнение (1.4):
Этому уравнению эквивалентна система
в которой переменные u и V связаны друг с другом.
Структура уравнения Шредингера
показывает, что оно отображает закон сохранения энергии.
Уравнение Шредингера определяет зависимость волновой функции от времени и от координат. Как второй закон Ньютона описывает траекторию частицы, так уравнение Шредингера описывает эволюцию волновой функции.
Выход в комплексную плоскость является следствием требования, чтобы волновая функция в любой момент времени полностью определялась её начальным значением. Следовательно, уравнение Шредингера должно содержать только первую производную волновой функции по времени, но не вторую. Если ограничиться гармоническими функциями в действительной области, то волновое уравнение обязано содержать вторую производную. В самом деле, однократное дифференцирование переводит синус в косинус и наоборот. Но колебания могут быть описаны экспонентой с комплексным показателем. Её важное свойство заключается в том, что первая производная функции возвращает нас к ней самой:
Перейдём к обсуждению физического смысла волновой функции.
2.1. Волновая функция
Выкладки предыдущего раздела мы проводили, используя представление классической механики о волновом пакете. В уравнении Шредингера функция Y ( r , t ) приобретает новый смысл. Она называется волновой функцией и описывает уже не суперпозицию колебаний, но состояние реальной частицы. Перечислим основные свойства волновой функции.
Волновая функция как вероятность
В квантовой механике вся информация о частице содержится в её волновой функции. С учётом соотношения неопределённостей, эта информация носит вероятностный характер. А именно, квадрат модуля волновой функции пропорционален вероятности W найти частицу в данной точке в заданный момент времени:
Здесь звёздочка означает комплексное сопряжение. В большинстве задач, которые нам встретятся в дальнейшем, имеет место точное равенство:
Выбор между (2.1) и (2.2) определяется степенью локализации частицы в пространстве. Если вероятность найти частицу в удалённых точках исчезающе мала, то интеграл
взятый по всему пространству, сходится. В конечном итоге именно это и делает возможным равенство (2.2). Наоборот, свободно движущаяся частица может быть обнаружена в любой точке. Интеграл (2.3) для её волновой функции расходится и, следовательно, | Y | 2 не может служить вероятностью никакой величины. В этом случае справедливо отношение
которое является следствием (2.1). Ниже нам неоднократно будут встречаться волновые функции, модуль которых не стремится к нулю при удалении от начала координат, либо убывает слишком медленно. Хотя для таких функций не имеет смысла (2.2), тем не менее, отношение значений W в двух разных точках пространства равно отношению вероятностей обнаружить там частицу.
Принцип суперпозиции
Уравнение Шредингера линейно относительно волновой функции. Следовательно, любая линейная комбинация
его решений Y 1 и Y 2 также является его решением.
Таким образом, линейная комбинация волновых функций обязательно описывает некоторое состояние частицы (или системы частиц). В частности, при C2 = 0 получаем, что решение уравнения Шредингера, известно с точностью до постоянного множителя.
Нормировка
Вероятность W по своему смыслу должна удовлетворять условию нормировки
Если частица совершает своё движение в ограниченной области, то, согласно предыдущему разделу, существует интеграл:
При выполнении последнего равенства волновая функция может быть преобразована так, чтобы условие
имело место даже в том случае, когда константа C не равна единице. А именно, условию (2.7) удовлетворяет функция
Согласно сказанному в предыдущем разделе, обе эти функции описывают одно и то же состояние. Процесс перехода от Y к F называется нормировкой, а функция F — норми p ованной волновой функцией.
8.3 Ток вероятности
В газодинамике известно уравнение непрерывности для потока вещества
где r — плотность, а
поток вещества, движущегося со скоростью v . Оно справедливо в том случае, если нет источников и стоков частиц. Аналогичное соотношение
можно вывести и для плотности вероятности W . Сначала проведём расчёты для одномерного случая. Для определения вектора тока вероятности S воспользуемся уравнением Шредингера (1.4) для свободной частицы. Запишем его также для комплексно–сопряжённой волновой функции:
то, подставляя сюда выражения (1.4) и (3.4) для производных по времени от Y и Y *, находим
Последнее уравнение представляет собой аналог одномерного уравнения непрерывности, если поток вероятности принять равным
Обобщение на случай трёх измерений даёт уравнение непрерывности (3.3) с дивергенцией вектора
Физический смысл определённого таким образом потока вероятности S можно выяснить, вычислив его для свободной частицы, то есть, для волновой функции вида
Производная 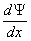
Аналогично вычисляем производную от комплексно сопряжённой функции:
Подставляя (3.7) и (3.7а) в (3.5), получаем
Нетрудно убедиться, что в трёхмерном случае мы приходим к формуле
Она полностью аналогична (3.2), где роль плотности выполняет плотность вероятности W, а вместо потока массы j надо подставить вектор S.
Поток вероятности равен нулю в случае действительной волновой функции. Следовательно, последняя описывает финитное движение, то есть, движение в ограниченной области пространства.
8.4 Операторы физических величин
В этом разделе мы соберём вместе явные выражения для самых важных для нас операторов. Оператор энергии сводится к дифференцированию по времени:
а оператор проекции импульса на одну из координат — к дифференцированию по этой координате:
Аналогичные формулы справедливы для проекций момента на две другие оси, а в трёхмерном случае
вектор импульса выражается через оператор градиента:
При формировании операторов можно пользоваться соотношениями между классическими величинами. Так, оператор кинетической энергии 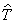
выражается посредством оператора Лапласа:
В отсутствие внешних полей полная энергия частицы равна её кинетической энергии:
В квантовой механике этому факту соответствует уравнение Шредингера для свободной частицы:
Последняя формула является обобщением (1.4) на случай трёх измерений.
Оператор координаты сводится к простому умножению на эту координату. То же самое справедливо и для оператора, представляющего любую функцию координат. Например,
В последующих разделах мы познакомимся с оператором момента вращения.
С математической точки зрения уравнения квантовой механики сводятся к линейной задаче на собственные значения с заданными граничными условиями.
Здесь Y i — собственные функции, а G i — собственные значения оператора 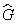
Спектр собственных значений может быть как дискретным, так и непрерывным. Например, непрерывным является спектр импульса свободной частицы. Покажем это для одномерного случая. Вычислим собственное значение p проекции импульса на ось x :
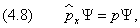
Решение последнего уравнения
в комплексной форме выражает «мгновенную фотографию» плоской монохроматической волны, распространяющейся вдоль оси x . Не удивительно, что мы получили именно такое решение, так как мы исходили из представления плоских волн при получении уравнения Шредингера. Временнýю часть волновой функции мы установим позже.
Отметим важную особенность функции (4.10): квадрат её модуля равен константе |C| 2 . Следовательно, свободно летящая частица с равной вероятностью может находиться в любой точке пространства. Как уже было сказано в разделе (2.1), такую функцию невозможно нормировать приведённым там способом. Таким образом, она представляет собой пример волновой функции, квадрат модуля которой пропорционален вероятности в смысле (2.4), но не имеет места (2.1).
Среднее значение.
В этом разделе мы с самого начала предполагаем, что волновая функция квадратично интегрируема, то есть существует интеграл (2.6). Как известно из математики, среднее значение 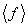
Для операторов, зависящих только от координат, это определение без всяких изменений переносится в квантовую механику. Нужно только вместо вероятности написать квадрат модуля волновой функции:
Здесь интегрирование ведётся по всей области изменения аргумента x .
В общем случае, когда физическая величина G не является функцией координат (например, импульс), её среднее значение определяется как
Подынтегральная функция состоит из двух сомножителей: Y * ( x ) и 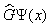
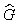
Пусть система находится в определённом состоянии, соответствующем собственному значению G i и собственному вектору — волновой функции Y i . Если физическую величину G усреднять с помощью функции Y i , то среднее значение 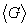
http://habr.com/ru/post/385535/
http://heritage.sai.msu.ru/ucheb/Zemcov/Part_2_Quant_ther/Chapter_08/Chapter_08.htm