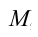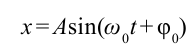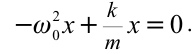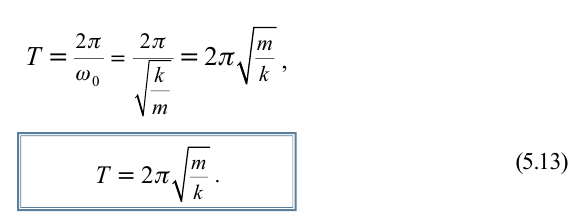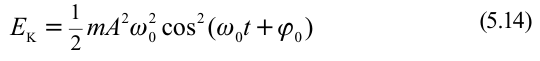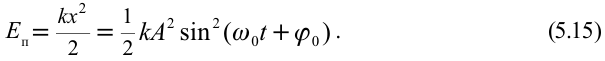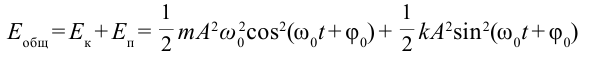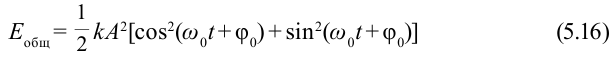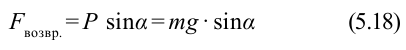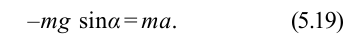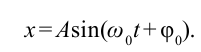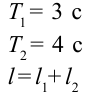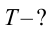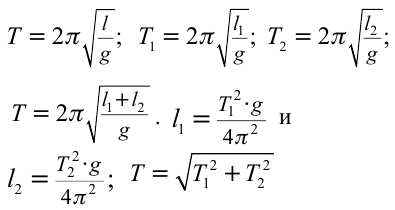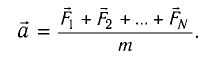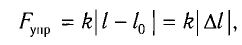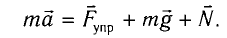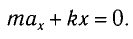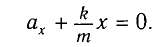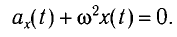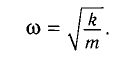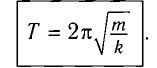Уравнение для поступательного движения маятника

ЛАБОРАТОРНАЯ РАБОТА № 108

Цель работы: Определение момента инерции маятника Максвелла.

Приборы и принадлежности: маятник Максвелла FРМ-03, комплект сменных колец.

Теоретическое введение

Момент инерции – аналог массы. Как масса является мерой инертности при поступательном движении, так и момент инерции является мерой инертности при вращательном движении. При вращении тела вокруг различных осей моменты инерции различны. Величина момента инерции относительно какой-нибудь оси определяется пространственным распределением элементарных масс тела – геометрией тела. Аналитическое вычисление величины момента инерции производится путем интегрирования выражения

где r — плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения.

При сложной форме поверхности тела и неравномерном распределении плотности аналитический подсчет величины момента инерции может быть достаточно сложной задачей.

Экспериментальное же определение момента инерции осуществить легко. В настоящей работе измеряется момент инерции металлических колец с помощью маятника Максвелла.

Маятник Максвелла – небольшой ролик, насаженный туго на ось, опускается под действием силы тяжести на двух нитях, предварительно намотанных на ось диска (рис.1).

Нити во время движения вниз разматываются до полной длины, раскрутившийся диск продолжает вращательное движение и наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, диск опять будет опускаться вниз и т.д. Диск будет совершать колебания вверх и вниз, поэтому такое устройство называется маятником.

Уравнение движения маятника Максвелла можно записать, используя основной закон динамики поступательного и вращательного движений. Уравнения движения маятника Максвелла без учета сил трения имеют вид:

Для поступательного движения, исходя из II законы Ньютона

А для вращательного движения

Связь между тангенциальным ускорением ( ) поступательного движения и угловым ускорением ( ) вращательного движения имеет вид:

где m — масса маятника, J — момент инерции маятника,
T — натяжение одной нити, r -радиус оси маятника вместе с намотанной на нее нитью подвески.

Ускорение a может быть найдено через измеренное время движения t и проходимое маятником расстояние h из известного уравнения

Из уравнений (1) – (4) может быть получена расчетная формула для момента инерции маятника Максвелла:

где D – внешний диаметр оси маятника вместе с намотанной на нее нитью подвески определяется по формуле

где D₀ – диаметр оси маятника в м; D_n – диаметр нити подвески в м; h – длина маятника, равная высоте, на которую он поднимается в м; m – масса маятника вместе с кольцом в кг.

где m₀ – масса оси маятника в кг; m_р – масса ролика в кг; m_к – масса кольца, аксиально положенного на ролик в кг.

Описание рабочей установки и метода измерений

Параметры маятника:

• максимальная длина маятника h = 410 мм;

• количество сменных колец 3;

• размеры маятника: диаметр оси маятника D₀ = 10 мм;

внешний диаметр ролика D_р= 86 мм;

внешний диаметр колец D_к= 105 мм;

диаметр нити подвески D_n= 0,5 мм.

Общий вид маятника FРМ показан на рис. 2.

SHAPE \* MERGEFORMAT

Рис. 2. Маятник Максвелла

Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, к которой прикреплен неподвижный верхний кронштейн 4 и подвижный нижний 5. На верхнем кронштейне находится электромагнит 6, фотоэлектрический датчик №1-7 и вороток 8 для закрепления и регулирования длины бифилярной подвески маятника.

Нижний кронштейн вместе с прикрепленным к нему фотоэлектрическим датчиком №2-9 можно перемещать вдоль колонки и фиксировать в произвольно избранном положении.

Маятник 10 – это ролик, закрепленный на оси и подвешенный по бифилярному способу, на который накладываются сменные кольца 11, изменяя, таким образом, момент инерции системы.

Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале на колонке прибора. С целью облегчения этого измерения нижний кронштейн оснащен красным указателем, помещенным на высоте оптической оси нижнего фотоэлектрического датчика.

Ход работы

1. Включить сетевой шнур измерителя в сеть, нажать клавишу «СЕТЬ», проверяя, все ли индикаторы измерителя высвечивают цифру ноль, и засветилась ли лампочка фотоэлектрического датчика?

2. Нижний кронштейн прибора передвинуть и зафиксировать в крайнем положении.

3. На ролик маятника надеть кольцо, прижимая его до упора.

4. На ось маятника намотать нить подвески и зафиксировать ее. Проверить, отвечает ли нижняя грань кольца нулю шкалы на колонке. Если нет, отвинтить верхний кронштейн и отрегулировать его высоту. Привинтить верхний кронштейн.

5. Нажать клавишу «ПУСК» миллисекундомера FРМ-03.

6. Открутить гайку воротка для регулирования длины бифилярной подвески. Определить длину нити таким образом, чтобы край стального кольца после опускания маятника находился на 2 мм ниже оптической оси нижнего фотоэлектрического датчика. Одновременно произвести корректировку установки маятника, чтобы его ось была параллельна основанию прибора. Закрутить гайку воротка.

7. Отжать клавишу «ПУСК» миллисекундомера FРМ-03.

8. Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно.

9. Зафиксировать маятник при помощи электромагнита.

10. Повернуть маятник в направлении его движения на угол около 5 0 .

11. Нажать клавишу «СБРОС».

12. Нажать клавишу «ПУСК».

13. Определить значение времени падения маятника. Опыт повторить 5 раз.

14. Определить значение среднего времени падения маятника по формуле где n – количество выполненных замеров; t_i – значение времени, полученное в i-ом замере;
t > — среднее значение времени падения маятника.

15. Со шкалы на вертикальной колонке прибора определить длину маятника.

16. Используя формулу (6) и известные значения диаметров D₀ и D_n, определить диаметр оси вместе с намотанной на неё нитью.

17. По формуле (7) вычислить массу маятника вместе с аксиально наложенным кольцом. Значения масс отдельных элементов нанесены на них.

18. По формуле (5) определить момент инерции маятника.

19. Оценить погрешность результата измерений.

20. Данные результатов измерений и вычислений занести в таблицу.

Лабораторная работа № 1-3. Маятник Максвелла

Лабораторная работа № 1-3

Цель работы: познакомиться с основными понятиями кинематики и динамики поступательного и вращательного

движения. Экспериментально определить угловое ускорение и момент инерции маятника.

Приборы и принадлежности: маятник Максвелла, набор металлических накладных колец, втулки.

Описание экспериментальной установки.

Данная установка называется маятником Максвелла. Она служит для определения момента инерции тела. Небольшой диск (маховичок), туго надетый на ось опускается под действием силы тяжести на двух нитях, предварительно намотанных на ось маховичка. Нити во время движения разматываются до полной длины. Раскрутившийся маховичок по инерции продолжает вращательное движение в том же направлении и наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом вращение. Дойдя до верхней точки, диск опять опускается вниз и т. д. Маховичок будет совершать колебания вверх — вниз, поэтому данное устройство и называют маятником.

Общий вид маятника Максвелла приведён на рис. 1.

На основании 1 закреплена стойка 2, к которой прикреплены неподвижный верхний кронштейн 3 и подвижный кронштейн 4. На верхнем кронштейне находится электромагнит 5, фотоэлектрический датчик №1 6 и вороток с фиксатором 7 для закрепления и регулировки длины маятника.

Нижний кронштейн 4 с фотодатчиком № 2 8 можно перемещать вдоль стойки и фиксировать в выбранном положении. Маятник 9 — это диск, закрепленный на оси и подвешенный на двух нитях к неподвижному кронштейну. На диск накладываются сменные металлические кольца 10, изменяющие момент инерции системы. Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале стойки прибора. Сигналы с фотодатчиков служат для автоматического пуска и остановки миллисекундомера 11.

Основные теоретические сведения

Основы кинематики поступательного и вращательного движения тела.

Поступательным называется движение, при котором любая прямая, проведённая в теле, остаётся параллельной сама себе при движении тела.

Основными особенностями такого вида движения являются следующие обстоятельства:

— при поступательном движении все точки тела движутся совершенно одинаково, то есть имеют одну и ту же скорость, ускорение, траектории движения, совершают одинаковые перемещения и проходят одинаковый путь.

— в этом случае при описании движения тела его можно рассматривать как материальную точку.

Для описания поступательного движения тел вводят в рассмотрение следующие понятия:

Для характеристики быстроты перемещения тела в пространстве вводят понятие скорости :

, размерность скорости: , метр в секунду.

Физический смысл скорости: она показывает, какое перемещение совершает тело за единицу времени при равномерном движении.

(пример: означает, что тело за каждую секунду перемещается на 5 м.)

Вектор скорости направлен по касательной к траектории движения материальной точки.

Для характеристики быстроты изменения скорости по величине и направлению вводят понятие ускорения :

, размерность ускорения:, метр на секунду в квадрате.

Таким образом, ускорением называется векторная величина, равная первой производной по времени от мгновенной скорости тела.

Физический смысл ускорения: оно показывает, на сколько изменяется скорость тела за единицу времени при равнопеременном движении.

(например: означает, что скорость тела изменяется на за каждую секунду.)

Направление вектора ускорения совпадает с направлением вектора.

При прямолинейном движении тела ускорение сонаправлено с вектором в случае ускоренного движения тела и противоположно направлено при замедленном движении.

При криволинейном движении вектор ускорения в общем случае образует с вектором мгновенной скорости некоторый угол .

Вращательным называется движение, при котором все точки тела описываю окружности, центры которых лежат на одной и той же прямой, называемой осью вращения тела.

Основной особенностью такого вида движения является следующее обстоятельство:

при вращательном движении все точки абсолютно твёрдого тела движутся с одной и той же угловой скоростью и угловым ускорением и совершают одинаковые угловые перемещения.

Для описания вращательного движения тела вводят в рассмотрение следующие понятия:

Угол поворота — это угол, на который поворачивается радиус-вектор любой точки тела при его вращении.

, радиан.

Элементарное угловое перемещение можно рассматривать как вектор , направление которого определяется по правилу буравчика (правилу правого винта):

если рукоятку буравчика вращать по направлению вращения тела, то поступательное движение буравчика будет совпадать с направлением вектора (см. рис. 3).

Удобство такого введения в следующем:

— модуль вектора однозначно определяет величину элементарного поворота тела ,

— направление вектора через правило буравчика определяет направление вращения тела,

— положение вектора в пространстве определяет

ось вращения тела.

Для характеристики быстроты вращения тела в пространстве вводится понятие угловой скорости .

, размерность, радиан в секунду.

Угловая скорость есть первая производная по времени от угла поворота.

Физический смысл угловой скорости: она показывает, на какой угол поворачивается радиус-вектор любой точки тела за единицу времени при равномерном вращении.

(например: означает, что за каждую секунду радиус-вектор поворачивается на 2 радиана)

Направление угловой скорости совпадает с направлением вектора , то есть она также определяется по правилу буравчика.

Для характеристики быстроты изменения угловой скорости вводится понятие углового ускорения :

, размерность, радиан на секунду в квадрате.

Физический смысл углового ускорения: оно показывает, на сколько изменяется угловая скорость тела за единицу времени при равнопеременном вращении.

(например: означает, что за каждую секунду угловая скорость тела изменяется на .)

Направление вектора углового ускорения совпадает с направлением вектора , то есть оно сонаправлено с вектором при ускоренном вращении тела и противоположно направлено при замедленном вращении.

Векторы, направление которых связывают с направлением вращения, называются псевдовекторами или аксиальными в отличие от обычных векторов (,, и т. д.), которые называются полярными.

Основы динамики поступательного и вращательного движения тела.

Для описания взаимодействия одного тела на другое вводят понятие силы .

Сила – векторная величина, являющаяся мерой механического воздействия на тело других тел или полей и характеризующая величину и направление этого воздействия.

Под действием силы тело может:

— деформироваться (статическое проявление силы),

— приобретать ускорение (динамическое проявление силы).

Основным уравнением динамики поступательного движения тела является второй закон Ньютона.

Одной из формулировок этого закона является следующая:

В инерциальной системе отсчёта векторная сумма всех сил, действующих на тело, равна произведению массы этого тела на сообщённое ему ускорение.

,

где — сила, , Ньютон, — масса тела, , килограмм, — ускорение тела,.

Масса тела является одной из важнейших понятий динамики, характеризующая инертные и гравитационные свойства тела. Масса тела – величина аддитивная (то есть масса тела равна сумме масс всех его частей).

Опыт показывает, что при описании вращательного движения твёрдого тела, кроме величины и направления действующей на тело силы, важной характеристикой является ещё и точка приложения этой силы.

В связи с этим вводят в рассмотрение понятие момента силы .

Моментом силы относительно неподвижной точки О называется векторная величина, равная векторному произведению радиус-вектора , проведённого из точки О в точку приложения силы, на саму эту силу:

или , где, Ньютон. метр.

Вектор момента силы является аксиальным, то есть его направление определяется по правилу векторного произведения (или правилу правого винта):

если винт вращать от первого сомножителя в векторном произведении ко второму по кратчайшему повороту, то поступательное движение винта укажет направление искомого вектора (см. рис. 4)

Следует помнить, что перед применением этого правила необходимо совместить начала перемножаемых векторов.

Можно использовать более простое правило буравчика:

если рукоятку буравчика вращать по направлению действия силы, то поступательное движение буравчика будет совпадать с направлением вектора момента силы (см. рис. 5).

На рис. 4 и 5 вектор направлен перпендикулярно плоскости чертежа на нас.

При этом следует помнить, что начало вектора совпадает с точкой О,

сам вектор перпендикулярен одновременно векторам и , а его величину можно определить по формуле:

или ,

где — угол между векторамии , а величина называется плечом силы , , метр.

Плечом силы называется кратчайшее расстояние от точки О до линии действия силы (см. рис. 5).

Величина зависит от выбора точки О.

Моментом силы относительно неподвижной оси Z называется скалярная величина, равная проекции на эту ось вектора момента силы относительно любой точки О, выбранной на этой оси:

.

Величина не зависит от выбора точки О на этой оси Z .

Наблюдения показывают, что при рассмотрении вращательного движения тела, основной характеристикой инертных свойств тела является не масса этого тела , а величина, которая называется моментом инерции тела .

Различают момент инерции тела относительно точки и момент инерции тела относительно оси.

Моментом инерции тела относительно точки О называется величина равная ,

где — кратчайшее расстояние от точки О до элементарной массы тела .

Моментом инерции тела относительно оси Z называется величина равная ,

где — кратчайшее расстояние от оси Z до элементарной массы тела .

Основной особенностью момента инерции тела является то обстоятельство, что его величина зависит от выбора оси вращения тела и распределение массы тела относительно рассматриваемой оси. То есть в отличие от массы , одно и то же тело имеет бесконечное множество моментов инерции , в зависимости от выбора оси вращения. В общем случае момент инерции тела относительно произвольной оси можно рассчитать по формуле:

,

где , — это функция зависимости плотности тела от координат, а сам интеграл определяется по всему объёму данного тела.

Однако на практике моменты инерции тел обычно определяют опытным путём, в связи с тем, что математически определить момент инерции тела иногда бывает очень сложно (более подробно о моменте инерции смотрите лабораторную работу 1-4).

Основным уравнением динамики вращательного движения тела является закон аналогичный второму закону

Ньютона, одной из возможных формулировок которого является следующая:

В инерциальной системе отчёта алгебраическая сумма моментов всех внешних сил , действующих на тело относительно неподвижной оси Z , равна произведению момента инерции этого тела относительно этой оси , на сообщённое ему угловое ускорение e :

.

Уравнения для поступательного и вращательного движения маятника без учёта сил сопротивления воздуха в нашем случае имеют вид:

где m — полная масса маятника, кг, I — момент инерции маятника, кг. м2, g — ускорение свободного падения, м/с2,

r — радиус оси маятника, м, Т — сила натяжения нити (одной), Н, — ускорение поступательного движения центра масс маятника, м/с2, e — угловое ускорение маятника, рад/с2.

Так как уравнение вращательного движения маховичка относительно оси вращения: ,

где — результирующий момент действующих на маятник сил относительно оси вращения, то с учетом уравнения (1), момент действующих сил можно определить по формуле:

.

Упражнение 1. Определение углового ускорения маятника и его дисперсии

1. Установите при помощи подвижного кронштейна высоту падения маятника h , заданную преподавателем. При помощи воротка с фиксатором 7 отрегулируйте длину нитей маятника Максвелла. Следите за тем, чтобы ось маятника была расположена горизонтально.

2. На диск маятника наложите стальное кольцо и запишите его массу mк . Убедитесь, что край стального кольца находится примерно на 2 мм ниже оптической оси нижнего фотоэлектрического датчика. Если нет, отрегулируйте высоту нижнего кронштейна с фотоэлектрическим датчиком. Замерьте радиус оси маятника .

3. Включите кнопку «СЕТЬ».

4. Нажмите кнопку «СБРОС» чтобы убедиться, что на табло установились нули.

5. Аккуратно вращая диск маятника, намотайте на его ось нить и зафиксируйте его в верхнем положении при помощи электромагнитов. При этом следите за тем, чтобы нити наматывались на ось виток к витку.

6. Нажмите кнопку «ПУСК» на передней панели миллисекундомера, удерживая её в течение одной секунды.

При этом маятник начнёт двигаться вниз, а таймер производить отсчет времени. В момент пересечения маятником оптиче ской оси фотодатчика отсчет времени должен прекратиться.

7. Прочитайте измеренное значение времени падения маятника и занести его в таблицу 1.

8. Нажмите кнопку «СБРОС» и приведите маятник в исходное положение (то есть зафиксируйте его в верхнем положении

при помощи электромагнита).

9. Аналогично проведите ещё четыре замера времени падения маятника с заданной высоты. Результаты занесите в таблицу 1.

h = mк = = Таблица 1

Пружинные и математические маятники в физике — виды, формулы и определения с примерами

Содержание:

Пружинные и математические маятники:

Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.

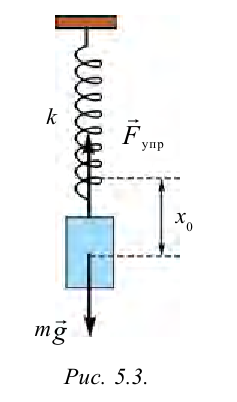
Система, состоящая из груза массой

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:

Если учесть, что ускорение тела, совершающего гармонические колебания 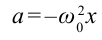, то уравнение (5.10) примет вид:

Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника.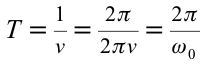

Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
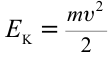
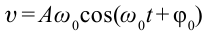
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, . В предыдущих темах было показано, что скорость можно выразить формулой . В таком случае кинетическая энергия маятника равна

Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:

В большинстве случаев важно знать полную энергию системы:

Если учесть, что ,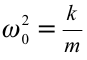

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
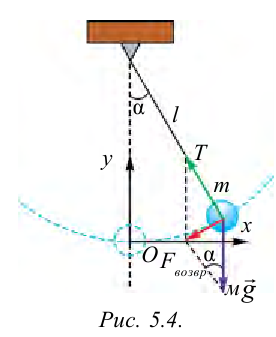
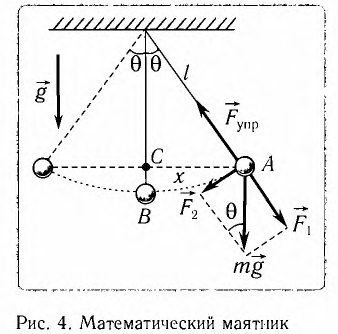
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.

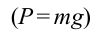
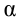
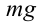
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки уравновешивает силу натяжения (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол , силы и не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.

Из рис. 5.4. видим, что:

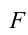
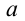
Согласно второму закону Ньютона, сила придает материальной точке ускорение , поэтому

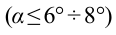
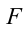
Из-за того, что угол наклона очень маленький , а сила направлена противоположно смещению, формулу (5.19) можно записать в виде

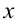
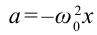
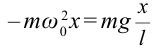
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой и учитывать соотношение , получим
Следовательно
Исходя из смысла периода колебания и учитывая, что 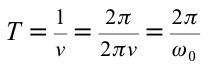получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:

1. при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
2. период колебания математического маятника также не зависит от массы подвешенного на него груза;
3. период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.

Отсюда колебание математического маятника записывается следующим выражением:

Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 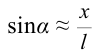и для решения уравнения движения не применяется закон синусов или косинусов.

Пример:

Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.

Решение: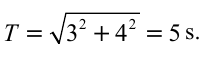

Ответ: 5 cек.

Пружинный и математический маятники

Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:

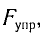
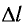
Закон Гука: модуль силы упругости , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) :

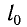
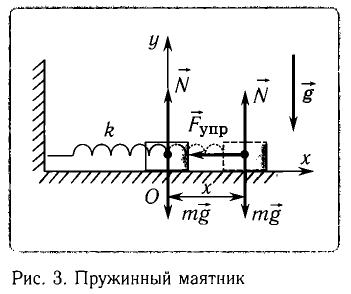
где k — жесткость тела, — длина недеформированного тела, l — длина деформированного тела.

Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.

Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).

Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 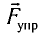направленная влево.

Запишем второй закон Ньютона для движения груза:

В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем

или

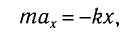
Это уравнение аналогично уравнению гармонических колебаний

Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:

Тогда период колебаний пружинного маятника можно найти по формуле

Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).

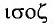
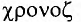
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов , — равный и — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.

Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.

Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).

Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.

Галилео Галилей экспериментально определил, что период малых колебаний (9

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.