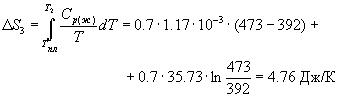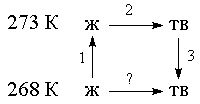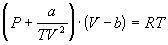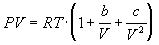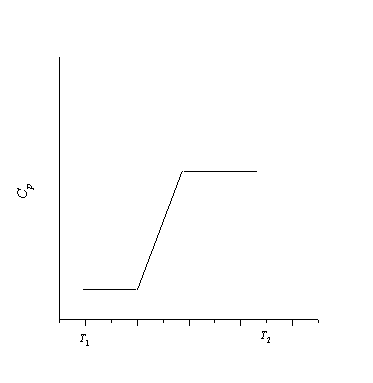Уравнение для расчета энтропии газа

Уравнение для расчета энтропии газа

Второй закон термодинамики устанавливает критерии необратимости термодинамических процессов. Известно много формулировок второго закона, которые эквивалентны друг другу. Мы приведем здесь только одну формулировку, связанную с энтропией.

Существует функция состояния — энтропия S, которая обладает следующим свойством: , (4.1) где знак равенства относится к обратимым процессам, а знак больше — к необратимым.

Для изолированных систем второй закон утверждает: dS і 0, (4.2) т.е. энтропия изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума (dS = 0,
d 2 S -23 Дж/К — постоянная Больцмана (k = R / N_A), W — так называемая термодинамическая вероятность, т.е. число микросостояний, которые соответствуют данному макросостоянию системы (см. гл. 10). Формулу (4.4) называют формулой Больцмана.

С точки зрения строгой статистической термодинамики энтропию вводят следующим образом:

, (4.5)

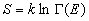
где G (E) — фазовый объем, занятый микроканоническим ансамблем с энергией E.

Термодинамическое определение энтропии основано на рассмотрении обратимых процессов:

. (4.6)

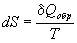
Это определение позволяет представить элементарную теплоту в такой же форме, как и различные виды работы:

Q_обр = TdS, (4.7)

где температура играет роль обобщенной силы, а энтропия — обобщенной (тепловой) координаты.

Расчет изменения энтропии для различных процессов

Термодинамические расчеты изменения энтропии основаны на определении (4.6) и на свойствах частных производных энтропии по термодинамическим параметрам:

(4.8)

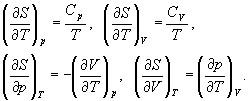
Последние два тождества представляют собой соотношения Максвелла (вывод см. в гл. 5).

1) Нагревание или охлаждение при постоянном давлении.

Количество теплоты, необходимое для изменения температуры системы, выражают с помощью теплоемкости: Q_обр = C_p dT.

(4.9)

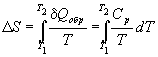
Если теплоемкость не зависит от температуры в интервале от T₁ до T₂, то уравнение (4.8) можно проинтегрировать:

. (4.10)

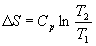
Если изменение температуры происходит при постоянном объеме, то в формулах (4.9) и (4.10) C_p надо заменить на C_V.

2) Изотермическое расширение или сжатие.

Для расчета энтропии в этом случае надо знать уравнение состояния системы. Расчет основан на использовании соотношения Максвелла:

(4.11)

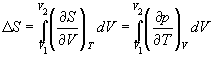
В частности, для изотермического расширения идеального газа (p = nRT / V)

(4.12)

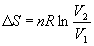
Этот же результат можно получить, если использовать выражение для теплоты изотермического обратимого расширения идеального газа: Q_обр = nRT ln(V₂/V₁)_.

3) Фазовые переходы.

При обратимом фазовом переходе температура остается постоянной, а теплота фазового перехода при постоянном давлении равна H_фп, поэтому изменение энтропии равно:

(4.13)

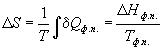
При плавлении и кипении теплота поглощается, поэтому энтропия в этих процессах возрастает: S_тв о С при давлении 1 атм. Мольная теплоемкость серы равна:

Температура плавления моноклинной серы 119 о С, удельная теплота плавления 45.2 Дж/г.

Решение. Общее изменение энтропии складывается из трех составляющих: 1) нагревание твердой серы от 25 до 119 о С, 2) плавление, 3) нагревание жидкой серы от 119 до 200 о С.

4.54 Дж/К.

2.58 Дж/К.

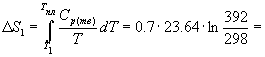
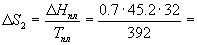
S = S₁ + S₂ + S₃ = 11.88 Дж/К.

Пример 4-3. Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются изотермически от объема V₁ до объема V₂: а) обратимо; б) против внешнего давления p.

Решение. а) Изменение энтропии газа при обратимом изотермическом расширении можно найти с помощью термодинамического определения энтропии с расчетом теплоты расширения по первому закону:

.

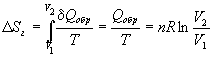
Так как расширение обратимое, то общее изменение энтропии Вселенной равно 0, поэтому изменение энтропии окружающей среды равно изменению энтропии газа с обратным знаком:

.

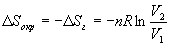
б) Энтропия — функция состояния, поэтому изменение энтропии системы не зависит от того, как совершался процесс — обратимо или необратимо. Изменение энтропии газа при необратимом расширении против внешнего давления будет таким же, как и при обратимом расширении. Другое дело — энтропия окружающей среды, которую можно найти, рассчитав с помощью первого закона теплоту, переданную системе:

.

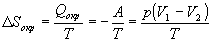
В этом выводе мы использовали тот факт, что U = 0 (температура постоянна). Работа, совершаемая системой против постоянного внешнего давления равна: A = p(V₂—V₁), а теплота, принятая окружающей средой, равна работе, совершенной системой, с обратным знаком.

Общее изменение энтропии газа и окружающей среды больше 0:

,

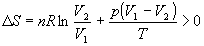
как и полагается для необратимого процесса.

Пример 4-4. Рассчитайте изменение энтропии 1000 г воды в результате ее замерзания при -5 О С. Теплота плавления льда при 0 о С равна 6008 Дж/моль. Теплоемкости льда и воды равны 34.7 и 75.3 Дж/(моль . К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс — самопроизвольный.

Решение. Необратимый процесс замерзания воды при температуре -5 О С можно представить в виде последовательности обратимых процессов: 1) нагревание воды от
-5 О С до температуры замерзания (0 О С); 2) замерзание воды при 0 О С; 3) охлаждение льда от 0 до -5 О С:

Изменение энтропии в первом и третьем процессах (при изменении температуры) рассчитывается по формуле (4.9):

77.3 Дж/К.

-35.6 Дж/К.

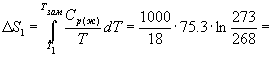
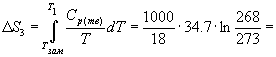
Изменение энтропии во втором процессе рассчитывается как для обычного фазового перехода (4.13). Необходимо только иметь в виду, что теплота при замерзании выделяется:

-1223 Дж/К.

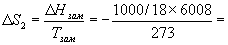
Т.к. энтропия — функция состояния, общее изменение энтропии равно сумме по этим трем процессам:

S = S₁ + S₂ + S₃ = -1181 Дж/К.

Энтропия при замерзании убывает, хотя процесс самопроизвольный. Это связано с тем, что в окружающую среду выделяется теплота и энтропия окружающей среды увеличивается, причем это увеличение больше, чем 1181 Дж/К, поэтому энтропия Вселенной при замерзании воды возрастает, как и полагается в необратимом процессе.

ЗАДАЧИ

4-1. Приведите пример термодинамического процесса, который может быть проведен как обратимо, так и необратимо. Рассчитайте изменение энтропии системы и окружающей среды в обоих случаях.

4-2. Проверьте неравенство Клаузиуса для циклического процесса, представленного в задаче 2.14.

4-3. Рассчитайте мольную энтропию неона при 500 К, если при 298 К и том же объеме энтропия неона равна 146.2 Дж/(моль . К).

4-4. Рассчитайте изменение энтропии при нагревании 11.2 л азота от 0 до 50 о С и одновременном уменьшении давления от 1 атм до 0.01 атм.

4-5. Один моль гелия при 100 о С и 1 атм смешивают с 0.5 моль неона при 0 о С и 1 атм. Определите изменение энтропии, если конечное давление равно 1 атм.

4-6. Рассчитайте изменение энтропии при образовании 1 м 3 воздуха из азота и кислорода (20 об.%) при температуре 25 о С и давлении 1 атм.

4-7. Три моля идеального одноатомного газа (C_V = 3.0 кал/(моль . К)), находящегося при T₁ = 350 K и P₁ = 5.0 атм, обратимо и адиабатически расширяются до давления P₂ = 1.0 атм. Рассчитайте конечные температуру и объем, а также совершенную работу и изменение внутренней энергии, энтальпии и энтропии в этом процессе.

4-8. Рассчитайте изменение энтропии при нагревании 0.4 моль хлорида натрия от 20 до 850 о С. Мольная теплоемкость хлорида натрия равна:

Температура плавления хлорида натрия 800 о С, теплота плавления 31.0 кДж/моль.

4-9. Рассчитайте изменение энтропии при смешении 5 кг воды при 80 о С с 10 кг воды при 20 о С. Удельную теплоемкость воды принять равной: C_p(H₂O) = 4.184 Дж/(г . К).

4-10. Рассчитайте изменение энтропии при добавлении 200 г льда, находящегося при температуре 0 о С, к 200 г воды (90 о С) в изолированном сосуде. Теплота плавления льда равна 6.0 кДж/моль.

4-11. Для некоторого твердого тела найдена зависимость коэффициента расширения от давления в интервале давлений от p₁ до p₂:

.

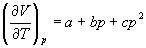
Насколько уменьшится энтропия этого тела при сжатии от p₁ до p₂?

4-12. Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются изотермически от давления p₁ до давления p₂: а) обратимо; б) против внешнего давления p 0 С и давлении 2 атм.

4-14. Нарисуйте график зависимости стандартной энтропии воды от температуры в интервале от 0 до 400 К.

4-15. Запишите энтропию одного моля идеального газа как функцию температуры и давления (теплоемкость считать постоянной).

4-16. Определите зависимость энтропии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля):

4-17. Определите зависимость энтропии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля):

4-18. Один моль газа описывается уравнением состояния

,

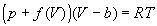
где f(V) — некоторая функция, которая не зависит от температуры. Рассчитайте изменение энтропии газа при его необратимом изотермическом расширении от объема V₁ до объема V₂.

4-19. Рассчитайте изменение энтропии 1000 г метанола в результате его замерзания при -105 О С. Теплота плавления твердого метанола при -98 о С (т.пл.) равна 3160 Дж/моль. Теплоемкости твердого и жидкого метанола равны 55.6 и 81.6 Дж/(моль . К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс — самопроизвольный.

4-20. Теплоемкость некоторого вещества в интервале температур от T₁ до T₂ изменяется следующим образом:

Постройте график зависимости энтропии вещества от температуры в этом интервале температур.

4-21. Пользуясь справочными данными, приведите пример самопроизвольной химической реакции, для которой стандартное изменение энтропии меньше 0.

4-22. Пользуясь справочными данными, рассчитайте стандартное изменение энтропии в реакции H_2(г) + ЅO_2(г) = H₂O_(г) а) при 25 о С; б) при 300 о С.

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Энтропия идеального газа

В этой статье мы расскажем, что такое энтропия идеального газа и в чем заключается ее физический смысл. Начнем с определения.

Энтропия – это функция состояния системы ( S ) с дифференциалом в бесконечном обратимом процессе, равным d S = δ Q T .

Параметр δ Q обозначает элементарное тепло, которое сообщается системе. Соответственно, T – это общая температура системы.

Если у системы в обратимом процессе изменяется знак энтропии, то это говорит о смене направления обмена теплом. Основная формула дает нам возможность найти, на сколько изменилась величина энтропии. Важно подчеркнуть, что она будет верной только в том случае, если процесс будет обратим.

В чем состоит физический смысл энтропии

Свойства идеального газа таковы, что с их помощью удобно пояснять физический смысл энтропии. Допустим, у нас есть один моль некоторого газа, для которого мы можем записать первое правило термодинамики (в дифференциальной форме):

δ Q = d U + p d V .

Выполним деление левой и правой части выражения на температуру. У нас получится, что:

δ Q T = d U T + p d V T = c μ V d T T + p d V T .

Здесь c μ V = i 2 R . С помощью уравнения Менделеева-Клайперона мы можем выразить из него p T и получить:

p V = R T → p T = R V .

Подставляем это в исходное выражение:

δ Q T = c м V d T T + R d V V = d c м V ln T + R ln V .

Правая часть уравнения у нас получилась полностью дифференциальной, значит, и слева тоже должен быть полный дифференциал. Назовем его d S . С помощью одной из приведенных выше формул вычислим ∆ S в изотермическом процессе. Если температура остается постоянной, то и внутренняя энергия системы также остается прежней. Получаем следующее:

d S = R d ln V → ∫ ( 1 ) ( 2 ) d S = R ∫ ( 1 ) ( 2 ) d ln V = S 2 — S 1 = R ln V 2 V 1 .

Нам известно, что объем, занимаемый газом в равновесном состоянии, связан с количеством пространственных микросостояний частиц формулой Г 0 = N ! N — n ! ( Г 0 – общее количество микросостояний, N – количество ячеек, в которые помещены частица системы, n – общее количество частиц). Поскольку исходный объем идеального газа равен одному молю, то n = N A . Выведем формулу объемов V 1 и V 2 из выражения выше. Она будет иметь следующий вид:

Г 01 = N 1 ! N 1 — N A ! , Г 02 = N 2 ! N 2 — N A ! .

Здесь N 1 = V 1 l 3 , N 1 = V 2 l 3 , l = 10 — 10 м .

Для дальнейших преобразований нам потребуется формула Стирлинга (для больших n , n ! ≈ N 2 N 1 N A = V 2 V 1 N A ):

Г 02 Г 01 ≈ N 2 N 1 N A = V 2 V 1 N A .

Берем логарифм от этого выражения и получаем:

ln V 2 V 1 = 1 N A ln Г 02 Г 01 .

Таким образом, S 2 — S 1 = R ln V 2 V 1 = R N A ln Г 02 Г 01 = k ln Г 02 — k ln Г 01 .

Здесь параметр k обозначает постоянную Больцмана.

Формула Больцмана

Сам вид формулы энтропии говорит нам о том, что она может быть определена через логарифм числа микросостояний, образующих макросостояние, рассматриваемое как S = k ln Г .

Выведенное выше равенство называется формулой Больцмана. Она позволяет сделать вывод, что чем больше упорядоченность системы, тем меньше в ней микросостояний, с помощью которых достигается макросостояние. Поэтому энтропия является мерой упорядоченности системы. Максимальная энтропия достигается в состоянии упорядоченности.

Энтропия является аддитивной величиной. При S = c o n s t процесс называется изоэнтропийным. Если система является физически однородной, то ее энтропия выражается как функция двух независимых параметров состояния (масса считается постоянной).

Условие: есть идеальный газ, в котором происходит изотермическое расширение, при этом объем меняется от V 1 до V 1 . При этом температура системы в первом процессе равна T 1 , а во втором T 2 , причем вторая температура меньше, чем первая. Определите, как будет меняться значение энтропии.

Зная основное определение энтропии и обратимость процессов в идеальном газе, мы можем использовать формулу для вычисления ∆ S при постоянной температуре.

∆ S = ∫ ( 1 ) ( 2 ) δ Q T = 1 T ∫ ( 1 ) ( 2 ) δ Q .

Идеальный газ в физике – это понятие, подразумевающее, что мы можем пренебречь взаимодействием между его молекулами. Если V = c o n s t , то работа идеального газа равна 0 .

Обратимся к первому правилу термодинамики, зная, что при постоянной температуре d U = 0 :

Выражаем давление из уравнения Менделеева-Клайперона:

p V = ν R T → p = v R T V .

Подставляем в исходную формулу и получаем:

∆ S = 1 T ∫ ( 1 ) ( 2 ) н R T V d V = R T н T ∫ ( 1 ) ( 2 ) d V V = v R ln V 2 V 1

Ответ: поскольку не существует зависимости энтропии от температуры в изотермическом процессе, то в заданных условиях оба процесса будут иметь одинаковую энтропию.

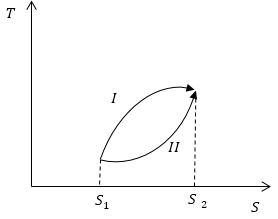
Условие: на рисунке схематично обозначены обратимые процессы. Сопоставьте, какие количества теплоты будут поглощаться системой в ходе обеих процессов.

Данная задача решается на основе определения энтропии для обратимых процессов.

Выражаем показатель δ Q из уравнения, выведенного ранее, и получаем:

Для определения объема подведенного к системе тепла нам нужно проинтегрировать выражение:

∆ Q = ∫ S 1 S 2 T d S .

Теперь, используя геометрическое свойство интеграла (по площади) и рисунок, мы можем подытожить, что площадь, ограниченная кривой процесса, изоэнтропами, перпендикулярными S , и осью S , больше площади для процесса 2 , значит, Q I > Q I I .

Ответ: в первом процессе поглощается большее количество теплоты, чем в во втором.

Изменение энтропии

Вы будете перенаправлены на Автор24

Энтропия – это фундаментальная физическая величина. Введение этого понятия завершило этап становления понятийного аппарата термодинамики. Следующим этапом развития этой науки было выяснение физического смысла энтропии.

Установление принципа Больцмана (формулы Больцмана) и таким образом связи между термодинамикой и статистической физикой, позволило энтропии покинуть пределы физики и войти в другие области знаний.

Энтропия – это общезначимое понятие, применяемое во множестве наук, например, в:

Введено это понятие было Р. Клаузиусом. Важные работы посвятил энтропии Л. Больцман, М. Планк.

Функция состояния полным дифференциалом которой является δQ/T называется энтропией ($S$):

где $\delta Q$ – элементарное тело, получаемое термодинамической системой; $T$- термодинамическая температура.

Отметим, что формула (1) справедлива только для обратимых процессов. Например, для процессов, проводимых в идеальном газе.

Важно, что выражение (1) определяет не саму энтропию, а ее изменение, или разность энтропий. При помощи данной формулы можно вычислить, каково изменение энтропии, если термодинамическая система переходит из одного состояния в другое, но нельзя понять, какова энтропия каждого из этих состояний.

Напомним формулу Больцмана для энтропии, так как она нам поможет понять физический смысл, процессов, которые происходят с энтропией:

$S=klnW\, \left( 2 \right)$

где ($W$) – термодинамическая вероятность (статистический вес состояния), то есть количество способов, реализации данного состояния термодинамической системы. $W$ ≥1; $k$- постоянная Больцмана.

Изменение энтропии, исходя из статистической формулы Больцмана, найдем как:

Готовые работы на аналогичную тему

Вычисление изменения энтропии в изотермическом процессе

Вычислим изменение энтропии в одном моле идеального газа при изотермическом процессе ($T=const$). Оттолкнемся от первого начала термодинамики в дифференциальной форме:

$\delta Q=dU+pdV\, \left( 3 \right)$,

где $dU$ — изменение внутренней энергии идеального газа; $pdV$=$\delta A$ – работа, совершаемая газом.

Найдем отношение всех слагаемых выражения (3) и температуры:

где $C_V$ – теплоемкость газа при $V=const$.

Для идеального газа справедливо уравнение Менделеева – Клапейрона, учитывая, что у нас 1 моль газа:

$\frac

=d\left( \ln T \right),\, \frac=d\left( \ln V \right)\left( 6 \right)$.

в этом случае мы можем записать для уравнения (4):

$\frac<\delta Q>=d\left( C_lnT+RlnV \right)\left( 7 \right)$.

По определению (1), и принимая во внимание (7), запишем:

$dS=d\left( C_lnT+RlnV \right)\left( 8 \right)$.

Формула (8) показывает нам, что в изотермическом процессе изменяется только второе слагаемое правой части:

• при увеличении объема энтропия увеличивается,
• с уменьшением объема энтропия уменьшается.

Данный результат очевиден, так как если увеличивается объем, то возрастает количество мест, которое смогут занять частицы при неизменяющемся их количестве. Следовательно, растет число разных возможностей расположения на этих местах (увеличивается количество пространственных микросостояний). Увеличение числа микросостояний означает увеличение энтропии (см формулу (2)).

Изменение энтропии в изохорическом процессе

Рассмотрим изохорный процесс в идеальном газе ($V=const$ или $dV=0$). Из формулы (7) для изохорного процесса следует:

$dS=d\left( C_lnT+RlnV \right)=d(C_lnT)\left( 9 \right)$.

После интегрирования (9), получим:

Формула (10) показывает, что в изохорическом процессе при увеличении температуры происходит рост энтропии. Данный результат можно пояснить так:

1. при увеличении температуры растет средняя энергия частиц газа;
2. увеличивается количество возможных энергетических состояний.

Изменение энтропии в адиабатном процессе

Адиабатный процесс характеризуется тем, что он происходит без теплообмена (δQ=0). Исследуя адиабатный процесс в идеальном газе, за основу для вычисления энтропии примем выражение (8). Найдем интеграл правой и левой частей этого выражения, получим:

Запишем уравнение адиабатного процесса в параметрах $T,V$:

где $\gamma =\frac>>-$ показатель адиабаты. Возьмем натуральные логарифмы от обеих частей выражения (12), имеем:

$\ln \left( \frac>> \right)=\left( \gamma -1 \right)\ln \left( \frac>> \right)=-\left( \gamma -1 \right)\ln \left( \frac>> \right)\left( 13 \right)$.

Преобразуем выражение (11), приняв во внимание формулу (13):

Вспомним соотношение Майера:

и сделаем вывод о том, что изменение энтропии в адиабатном процессе нет:

Адиабатный процесс является изоэнтропийным ($S=const$).

При адиабатном расширении газа увеличение энтропии может идти только за счет увеличения объема, но при этом происходит уменьшение температуры, и энтропия уменьшается из-за уменьшения температуры. Данные тенденции взаимно компенсируют друг друга.

Рассмотрим пример. Два сосуда разного объема содержат по $\nu$ молей одинакового идеального газа. Температуры газов равны $ T_1$ и $ T_2$. Сосуды соединяют, газы перемешиваются. Система приходит в состояние равновесия. Определим изменение энтропии в этом процессе.

Рисунок 1. Изменение энтропии в адиабатном процессе. Автор24 — интернет-биржа студенческих работ

Будем считать, что изобарное расширение каждого из газов до конечного объема является обратимым. В этом процессе температура каждой из газовых компонент изменяется до конечной температуры $\frac+T_<2>><2>$. Найдем изменение энтропии каждого из газов по отдельности:

$\Delta S_<1>=\int\limits_a^b \frac

=\nu c_

\ln \left(\frac+T_<2>><2T_<1>> \right)\left( 16 \right)$,

где $a=T_<1>;b=\frac+T_<2>><2>$ $c_p$ – молярная теплоемкость газа при постоянном давлении.

Изменение энтропии второго газа запишем аналогично:

$\Delta S_<2>=\nu c_

\ln \left( \frac+T_<2>><2T_<2>> \right)\left( 17\right)$.

Поскольку энтропия является аддитивной величиной, то полное изменение энтропии найдем как сумму:

источники:

http://zaochnik.com/spravochnik/fizika/termodinamika/entropija-idealnogo-gaza/

http://spravochnick.ru/fizika/termodinamika/izmenenie_entropii/