Уравнение для тока в общем виде
Повторим еще раз уравнения (1.14):
Согласно методу симметричных составляющих
Разделив левую и правую части последних выражений на wэB, получим

где k = wэВ/wэА— уже известный коэффициент трансформации двигателя. Подставляя (1.23) в выражение 

Рассчитав IA1 и IA2 , легко определить IB1 и IB2 , а затем найти полные токи фаз А и В.
§ 1.9. Электромагнитная мощность. Вращающий момент несимметричного двухфазного микродвигателя
Поскольку в рассматриваемых микродвигателях имеют место поля токов прямой и обратной последовательностей, электромагнитная мощность — мощность, передаваемая от статора к ротору магнитным полем, должна быть равна сумме мощностей этих последовательностей.
Как известно, при круговом поле электромагнитная мощность равна потерям в активном сопротивлении ротора, деленным на скольжение s для прямого и на 2 — s для обратного полей
| Pэм1 = Pэм1А + Pэм1В = I 2 рA1·rрA/s + I 2 pВ1·rpВ/s , | (1.25) |
| Pэм2 = Pэм2А + Pэм2В = I 2 рA2·rрA/2-s + I 2 pВ2·rpВ/2-s. | (1.26) |
Если выразить токи и сопротивления фазы В через токи и сопротивления фазы А
подставить в (1.25), (1.26), то после преобразований получим

Выражение (1.27) неудобно для практических расчетов тем, что в него входят токи ротора. Это обстоятельство можно обойти, если воспользоваться схемами замещения рис.1.7. Действительно, в параллельном соединении: “контур намагничивания — цепь ротора” (рис.1.7), существует только одно активное сопротивление rрA. В преобразованных схемах замещения рис.1.8 в состав ZрA1, ZрA2 тоже входит активное сопротивление rрA1, rрA2. Поэтому в соответствии с законом сохранения энергии потери мощности в этих сопротивлениях должны быть одинаковыми, т.е.
С учетом этого выражение электромагнитной мощности приобретает простой вид

Если разделить электромагнитную мощность на синхронную угловую частоту вращения, получим выражение вращающего момента
| М = Рэм/ω1 = Рэм1/ω1 – Рэм2/ω1. | (1.29) |
При этом перед электромагнитной мощностью обратной последовательности следует поставить знак «минус», ибо обратное поле создает не движущий, а тормозной момент.
На рис. 1.10 представлена механическая характеристика асинхронного двигателя при эллиптическом поле, как результат действия прямого и обратного полей, создающих вращающий М1 и тормозной М2 моменты.
Рис.1.10. Механическая характеристика двухфазного асинхронного двигателя с эллиптическим магнитным полем
Из рис. 1.10 видно негативное действие обратного поля:
- снижение максимального и пускового моментов,
- увеличение номинального скольжения и, как следствие, увеличение потерь в роторе, снижение КПД машины.
Задача 1.7. Определить пусковой момент несимметричного двухфазного двигателя, параметры схемы замещения которого
хсA = 26Ом; rсA = 34 Ом; xmA = 430 Ом; m = 2; rрA= 30 Ом; xрA = 22 Ом; f = 50 Гц; U = 220 В.
§ 1.10. Энергетическая диаграмма. Потери мощности
Энергетическая диаграмма несимметричного двухфазного микродвигателя показана на рис. 1.11.
Рис.1.12. Энергетическая диаграмма несимметричного двухфазного асинхронного микродвигателя
рк — потери в конденсаторе. pk = I²сB rк . Активное сопротивление конденсатора rк обычно очень мало, так чтопотерями в нем можно пренебречь.
pст— потери в стали. При эллиптическом поле они равны сумме потерь встали от прямого pст1 и обратного pст2 полей [1]: рст = рст1 + рст2
Потерями в стали ротора при скольженьях, близких к номинальному, можно пренебречь, поскольку частота перемагничивания ротора весьма небольшая ( f2 = f1s ).
Потери в стали статора от поля прямой последовательности рассчитывают обычным порядком [4]. Они пропорциональны квадрату индукции и частоте в степени 1,3:
| pст1≡ B² f 1.3 . | (1.30) |
Потери в стали статора от поля обратной последовательности
| рст2 = pст1 (EА2 /EА1)², | (1.31) |
где EА1, EА2 — ЭДС в обмотке А от поля прямой и обратной последовательностей.
Потери в обмотках А и В статора
В формуле (1.32) должны присутствовать токи статора, полученные сучетом потерь в стали. Эти токи определяются следующим образом [1,5].
Для покрытия потерь в стали двигатель потребляет из сетидополнительный ток, что приводит к увеличению активных составляющихтоков статора. Эти увеличения можно рассчитать по следующим формулам:
| IстА1 = pст1 /(2EА1 ) ; IстА2 = pст2 /(2EА2 ); | (1.33) |
| IстВ1 = IстА1 /k ; IстВ2 = IстА2 /k. | (1.34) |
Прибавляя «добавки» к активным составляющим токов, рассчитанным без учета потерь в стали, получим полные токи фаз статора:

Здесь индексы 1 и 2 означают прямую и обратную последовательности.
Потери в обмотке ротора можно определить через электромагнитнуюмощность (1.28) и скольжение ротора
| рэр = pэр1 + pэр2 = 2[I²A1rрA1s + I²A2rpA2(2 — s)]. | (1.36) |
Из энергетической диаграммы видно, что электрические потери в обмотке ротора от токов обратной последовательности рэр2 больше электромагнитной мощности обратной последовательности Рэм2, чего казалось бы не должно быть. Этот парадокс объясняется следующим образом.
По отношению к полю обратной последовательности машина работает в режиме электромагнитного тормоза, поэтому вся энергия (Рэм2) превращается в тепло, т.е. в потери в обмотке ротора. Но для вращения ротора против поля требуется еще и механическая энергия, источником которой является электромагнитная мощность прямой последовательности Рэм1. Часть этой мощности (Dpэр2) также превращается в тепло. Эта часть равна
Механическая мощность, развиваемая несимметричным двухфазным микродвигателем равна:
Механические потери pмех — потери на трение и вентиляцию, определяют по эмпирическим формулам [4], суть которых заключается в том, что эти потери пропорциональны квадрату скорости вращения рмех
Полезная мощность на валу микродвигателя

Потребляемая электрическая мощность
| P1 = PЭМ + pэс + pст + pк. | (1.38) |
| η = P2 /P1. | (1.39) |
| cosφA = IcAa /IcA; cosφB = IcBa /IcB. | (1.43) |
Ни в энергетической диаграмме, ни в расчетах не упоминалисьдобавочные потери. Согласно ГОСТ 183-74 они составляют 0,5 % отпотребляемой мощности, что практически выходит за пределы точностирасчетов микромашин.
Комплексные уравнения электрического состояния цепи.
Электрическое состояние цепей синусоидального тока, так же как и цепей постоянного тока, описывается с помощью уравнений, составленных в соответствии с законами Кирхгофа.
В общем виде тригонометрическое уравнение по первому закону Кирхгофа для узла цепи синусоидального тока имеет вид

где n – число ветвей, сходящихся в узле.
Этому уравнению соответствует уравнение первого закона Кирхгофа в комплексной форме (например, для действующих значений)

Правила знаков при составлении уравнений (58) остаются теми же, что и в цепях постоянного тока: токи, положительные направления которых направлены от узла, следует брать со знаком минус, а токи, положительные направления которых направлены к узлу – со знаком плюс.
Для любого контура цепи с синусоидальными напряжениями справедливо тригонометрическое уравнение, составленное по второму закону Кирхгофа.
В идеализированных электрических цепях магнитное поле считается сосредоточенным только на участках цепи, содержащих индуктивные элементы. При обходе замкнутого контура цепи всегда можно выбрать путь, лежащий вне переменного магнитного поля, а участок, содержащий индуктивный элемент, характеризовать разностью потенциалов, т. е. напряжением на его зажимах; при этом изменение потенциала в любом замкнутом контуре цепи синусоидального тока равно нулю. Поэтому, согласно второму закону Кирхгофа, алгебраическая сумма мгновенных значений напряжений всех участков замкнутого контура равна нулю:

где m — число участков, рассматриваемого контура.
Тригонометрическое уравнение можно заменить соответствующим ему комплексным уравнением второго закона Кирхгофа (например, для действующих значений)

Применительно к схемам замещения с источниками ЭДС второй закон Кирхгофа можно сформулировать таким образом: алгебраическая сумма комплексных напряжений на пассивных элементах замкнутого контура равна алгебраической сумме сторонних ЭДС, входящих в этот контур:

Правила знаков при составлении уравнений (60) и (61) остаются теми же, что и в цепях постоянного тока: слагаемые берут со знаком плюс в случае, когда направление обхода совпадает со стрелкой положительного направления соответственно напряжения, тока или ЭДС.
Последовательное соединение элементов в цепи синусоидального тока.
Рассмотрим в качестве примера цепь с последовательным включением резистора, индуктивной катушки и конденсатора. Такая цепь с достаточной точностью описывается схемой замещения, представленной на рисунке 13. Найдем связь между напряжением на входе цепи 
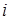
 |
Запишем уравнение по второму закону Кирхгофа в комплексной форме:

Выразим слагаемые правой части уравнения через комплексное значение тока 
и перепишем (62) в виде

Соотношение (63) является записью закона Ома рассматриваемой цепи в комплексной форме, а комплекс 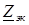

Таким образом, при последовательном соединении элементов цепи эквивалентное комплексное сопротивление цепи равно сумме комплексных сопротивлений всех последовательно включенных элементов, т. е. правило определения эквивалентного комплексного сопротивления последовательной цепи совпадает с аналогичным правилом для цепи постоянного тока. Очевидно, полученный результат справедлив для цепи с последовательным включением любого числа элементов.
Пример расчёта цепи синусоидального тока.
Произведём расчёт токов цепи синусоидального тока, представленной на рисунке 14.
 |

где 
Токи в схеме рисунка 14 можно рассчитать любым методом, аналогичным образом как для цепи постоянного тока.
Метод контурных токов.
В схеме рисунка 14 задаём направление неизвестных токов. Также выбираем направление контурных токов (например, по часовой стрелке). В схеме рисунка 14 можно выделить три контурных тока. Последовательные соединения 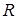


 |
Для схемы рисунка 15 получаем эквивалентные сопротивления

источники ЭДС в комплексной форме
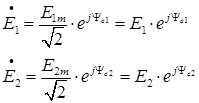
Для определения контурных токов необходимо составить следующую систему уравнений:

Уравнения для контурных токов можно записать в матричной форме:

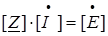
Решением уравнения (70) будет

Далее необходимо определить неизвестные токи через контурные токи:

Метод узловых потенциалов.
Аналогичным образом, как в методе контурных токов, представляем исходную схему в виде, представленном на рисунке 16.
 |
В схеме (рисунок 16) потенциал 

Уравнения для узловых потенциалов (73) можно записать в матричной форме:


где 


Решением уравнения (75) будет

Далее определяются токи

Баланс мощности.
Потребляемая полная мощность:

где 

Полная мощность источников:

где 

Потенциальная диаграмма.
Построим потенциальную диаграмму для левого контура, представленного на рисунке 17, исходной схемы (рисунок 14).
 |
На данном примере (рисунок 17) получаем

Если потенциалы (80) перенести на комплексную плоскость, то должна получиться замкнутая траектория. При этом, потенциал 
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.
Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Уравнение для тока в общем виде
1.7.2. Уравнение непрерывности
Если внутри проводника, по которому течет электрический ток, выделить какой-то объем, ограниченный замкнутой поверхностью S (рис 1.7.2), то, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время dt на dq = —Idt, тогда в интегральной форме можно записать:
Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда.
Дифференциальная форма записи уравнения непрерывности записывается так:
В случае постоянного тока распределение зарядов в пространстве должно оставаться неизменным:
— это уравнение непрерывности для постоянного тока (в интегральной форме).
Линии j в этом случае нигде не начинаются и нигде не заканчиваются. Поле вектора j не имеет источника. В дифференциальной форме уравнение непрерывности для постоянного тока .
http://zdamsam.ru/b54188.html
http://www.chem-astu.ru/chair/study/physics-part2/?p=64













